人教版八年级下册17.1 勾股定理 课后练习 (含解析)
文档属性
| 名称 | 人教版八年级下册17.1 勾股定理 课后练习 (含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 626.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-16 08:12:13 | ||
图片预览

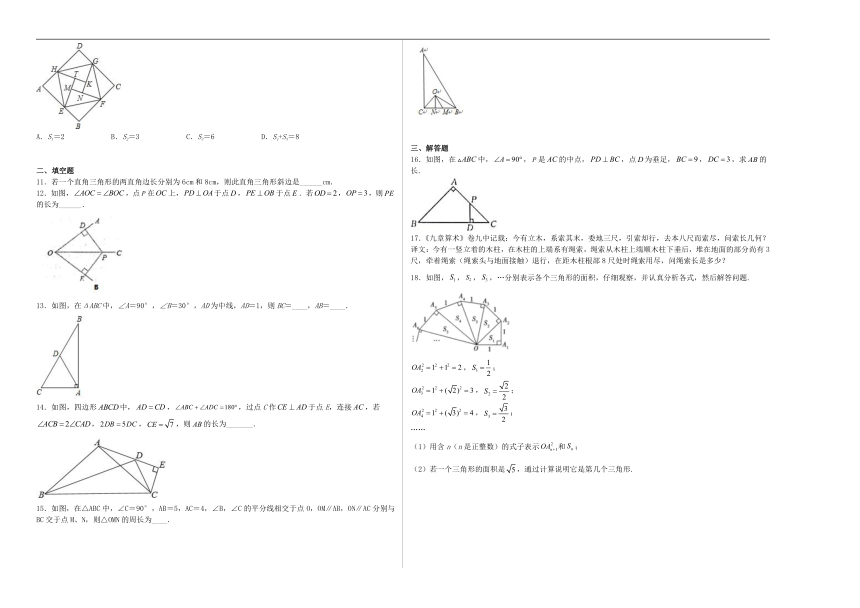

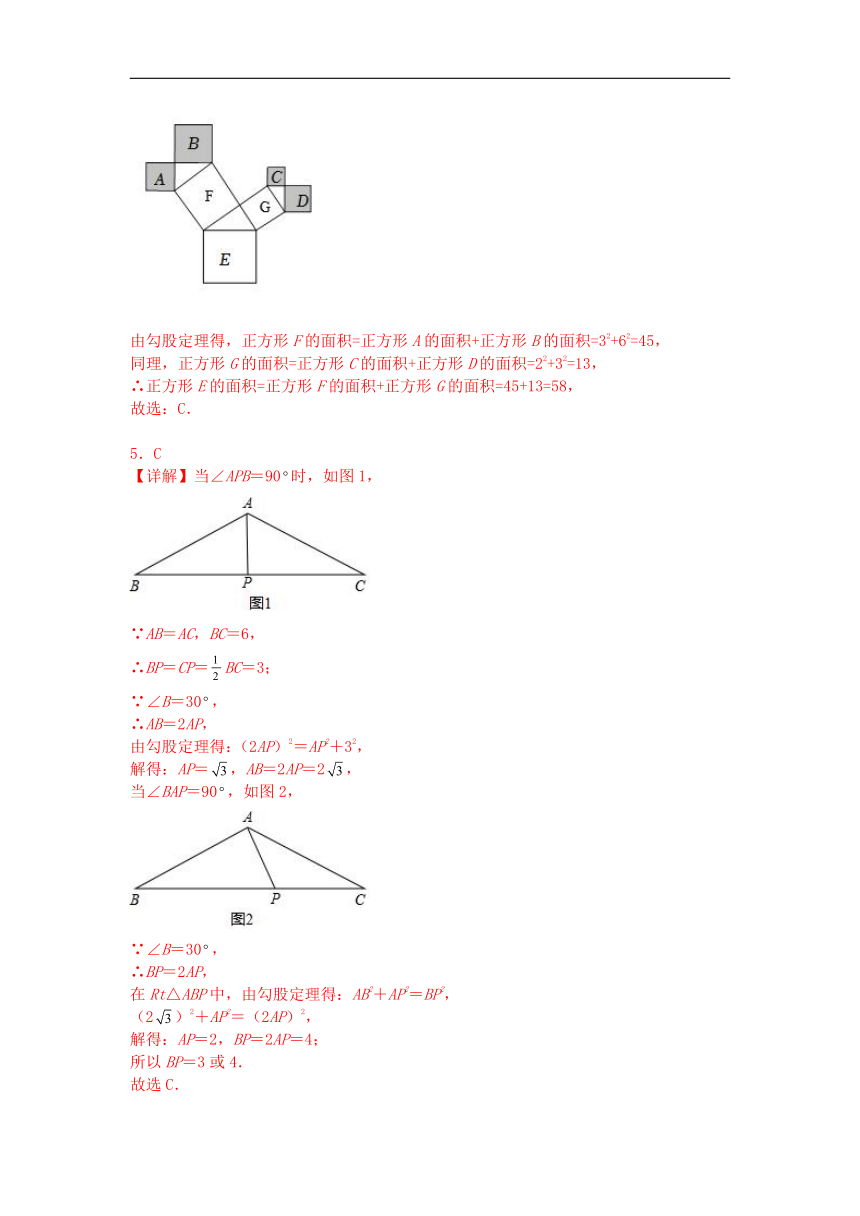
文档简介
17.1 勾股定理 课后练习
一、单选题
1.如图,在中,,D是BC的中点,垂足为D,交AB于点E,连接CE.若,,则BE的长为( )
A.3 B. C.4 D.
2.如图,以Rt△ABC的三边为边,分别向外作正方形,它们的面积分别为S1、S2、S3,若S1+S2+S3=16,则S1的值为( )
A.7 B.8 C.9 D.10
3.如图,圆柱的底面周长是24,高是5,一只在A点的蚂蚁想吃到B点的食物,沿着侧面需要爬行的最短路径是( )
A.9 B.13 C.14 D.25
4.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形、、、的边长分别是3、6、2、3,则最大正方形的面积是( )
A.14 B.34 C.58 D.72
5.已知等腰中,,, 底角为,动点从点向点运动,当是直角三角形是长为( )
A.4 B.2或3 C.3或4 D.3
6.已知直角三角形纸片的两条直角边长分别为和,过锐角顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则( )
A. B.
C. D.
7.如图,在长方形ABCD中,分别按图中方式放入同样大小的直角三角形纸片.如果按图①方式摆放,刚好放下4个;如果按图②方式摆放,刚好放下3个.若BC=4a,则按图③方式摆放时,剩余部分CF的长为( )
A. B. C. D.
8.如图,已知一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28海里/时的速度向正东方向航行,半小时后到达B处,在B处看见灯塔M在北偏东15°方向,此时灯塔M与渔船的距离是( )
A.7海里 B.14海里 C.7海里 D.14海里
9.如果一个直角三角形的两条边长分别为和,那么这个三角形的第三边长为( )
A. B. C. D.或
10.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=12,则下列关于S1、S2、S3的说法正确的是( )
A.S1=2 B.S2=3 C.S3=6 D.S1+S3=8
二、填空题
11.若一个直角三角形的两直角边长分别为6cm和8cm,则此直角三角形斜边是______cm.
12.如图,,点在上,于点,于点.若,,则的长为______.
13.如图,在ΔABC中,∠A=90°,∠B=30°,AD为中线,AD=1,则BC=____,AB=____.
14.如图,四边形中,,,过点C作于点E,连接,若,,,则的长为_______.
15.如图,在△ABC中,∠C=90°,AB=5,AC=4,∠B,∠C的平分线相交于点O,OM∥AB,ON∥AC分别与BC交于点M、N,则△OMN的周长为____.
三、解答题
16.如图,在中,,是的中点,,点为垂足,,,求的长.
17.《九章算术》卷九中记载:今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽,问索长几何?译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索(绳索头与地面接触)退行,在距木柱根部8尺处时绳索用尽,问绳索长是多少?
18.如图,,,,…分别表示各个三角形的面积,仔细观察,并认真分析各式,然后解答问题.
,;
,;
,;
……
(1)用含n(n是正整数)的式子表示和;
(2)若一个三角形的面积是,通过计算说明它是第几个三角形.
参考答案
1.D
【详解】解:∵,,,
∴,
∵,D是BC的中点,垂足为D,
∴BE=CE,
故选:D.
2.B
【详解】解:∵由勾股定理得:AC2+BC2=AB2,
∴S2+S3=S1,
∵S1+S2+S3=16,
∴2S1=16,
∴S1=8,
故选:B
3.B
【详解】解:该圆柱的侧面展开图,如下图所示,
根据两点之间线段最短,可知沿着侧面需要爬行的最短路径即为AB,
AB恰为一个矩形的对角线,该矩形的长为圆柱的底面周长的一半,
即长为24÷2=12,
宽为5,
∴AB==13,
即沿着侧面需要爬行的最短路径长为13.
故选:B.
4.C
【详解】解:如图,
由勾股定理得,正方形F的面积=正方形A的面积+正方形B的面积=32+62=45,
同理,正方形G的面积=正方形C的面积+正方形D的面积=22+32=13,
∴正方形E的面积=正方形F的面积+正方形G的面积=45+13=58,
故选:C.
5.C
【详解】当∠APB=90时,如图1,
∵AB=AC,BC=6,
∴BP=CP=BC=3;
∵∠B=30,
∴AB=2AP,
由勾股定理得:(2AP)2=AP2+32,
解得:AP=,AB=2AP=2,
当∠BAP=90,如图2,
∵∠B=30,
∴BP=2AP,
在Rt△ABP中,由勾股定理得:AB2+AP2=BP2,
(2)2+AP2=(2AP)2,
解得:AP=2,BP=2AP=4;
所以BP=3或4.
故选C.
6.B
【详解】解:如图,ABD是等腰三角形,ACD是等腰直角三角形,
∴AD=BD=n-m,
根据勾股定理得:m2+m2=(n m)2,
∴2m2=n2 2mn+m2,
m2+2mn n2=0.
故选:B.
7.A
【详解】解:∵BC=4a,
∴图①中,BE=a,图②中,BE=a,
∴小直角三角形的斜边长为,
∴图③中纸盒底部剩余部分CF的长为4a-2×a=a;
故选:A.
8.A
【详解】解:由已知得,AB=×28=14km,∠MAB=30°,∠ABM=105°.
过点B作BN⊥AM于点N.
∵在直角△ABN中,∠BAN=30°
∴BN=AB=7km.
在直角△BNM中,∠MBN=45°,
则直角△BNM是等腰直角三角形,
即BN=MN=7km,
∴BM===km.
故选:A.
9.D
【详解】解:当6和10是两条直角边时,
第三边=,
当6和10分别是一斜边和一直角边时,
第三边==8,
所以第三边可能为8或2.
故选:D.
10.D
【详解】解:八个直角三角形全等,四边形ABCD,EFGH,MNKT是正方形,
,,
,
,
,
,
,
,
,
,
,
,
故选:D.
11.10
【详解】解:由勾股定理得,直角三角形的斜边为cm.
故答案为:10
12..
【详解】因为∠AOC=∠BOC, 所以OC平分∠AOB又因为PD⊥OA,PE⊥OB,
所以PD=PE,
在直角三角形ODP中,OD=2,OP=3,所以由勾股定理得,
所以PE=,
故答案为:.
13.
【详解】解:∵在ΔABC中,∠A=90°,∠B=30°,
∴∠C=180°-∠CAB-∠B=180°-90°-30°=60°,BC=2AC,
∵AD为中线,
∴BD=CD=,
∴△DCA为等边三角形,
∵AD=1,
∴CD=AD=AC=1,
∴BC=2CD=2,
根据勾股定理AB=;
故答案为:2;.
14.
【详解】解:作DF⊥BC,DG⊥AB,
∵AD=CD,
∴∠DAC=∠DCA,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠CDE,
∵∠CDE=∠DAC+∠DCA=2∠DAC =∠CDE,
∴∠ABC=∠CDE=∠ACD
∴∠BAD=∠GAC-∠DAC=∠ABC+∠ACB-∠DAC=2∠DAC +2∠DAC -∠DAC =3∠DAC,
∵DA=DC,∠AGD=∠DFC,∠GAD=∠FCD,
∴,
∴DG=DF,
∴DB为∠ABC的角平分线,
∴∠ABD=,
作AH⊥BD,
∵AB=AC,∠ABH=∠EAC=∠DAC,∠AHB=∠CEA=90°,
∴,
∴AH=CE=,
∵∠AHD=∠BHC,∠HBC=∠HAD=∠DAC,
∴∠HAD=∠HCB=∠CDE,
∵AD=DC,∠HAD=∠HCB=∠CDE,∠AHD=∠E=90°,
∴,
∴HD=ED,
设BD=5x,AD=DC=2x,HD=ED=y,
由BH=AE得5x-y=2x+y,
∴,
在中,
,
∴x=2,
在中,AB=.
故答案为:.
15.
【详解】解:∵∠ACB=90°,AB=5,AC=4,
∴,
∵BO平分∠ABC,OM∥AB,
∴∠OBC=∠ABC,∠ABC=∠OMC,
又∵∠OMC=∠OBC+∠MOB,
∴∠OBC=∠MOB,
∴OM=MB,
同理可得ON=NC,
∴△OMN的周长=ON+NM+OM=NC+NM+MB=BC=3,
故答案为3.
16.
【详解】解:连接.设,
∵, ,
∴ , , ,
∴
,
∴.
故答案为.
17.
【详解】设绳索长为x尺
∴根据题意得:
解得.
∴绳索长为尺.
18.
【详解】(1),.
(2)当时,,即,
所以它是第20个三角形.
一、单选题
1.如图,在中,,D是BC的中点,垂足为D,交AB于点E,连接CE.若,,则BE的长为( )
A.3 B. C.4 D.
2.如图,以Rt△ABC的三边为边,分别向外作正方形,它们的面积分别为S1、S2、S3,若S1+S2+S3=16,则S1的值为( )
A.7 B.8 C.9 D.10
3.如图,圆柱的底面周长是24,高是5,一只在A点的蚂蚁想吃到B点的食物,沿着侧面需要爬行的最短路径是( )
A.9 B.13 C.14 D.25
4.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形、、、的边长分别是3、6、2、3,则最大正方形的面积是( )
A.14 B.34 C.58 D.72
5.已知等腰中,,, 底角为,动点从点向点运动,当是直角三角形是长为( )
A.4 B.2或3 C.3或4 D.3
6.已知直角三角形纸片的两条直角边长分别为和,过锐角顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则( )
A. B.
C. D.
7.如图,在长方形ABCD中,分别按图中方式放入同样大小的直角三角形纸片.如果按图①方式摆放,刚好放下4个;如果按图②方式摆放,刚好放下3个.若BC=4a,则按图③方式摆放时,剩余部分CF的长为( )
A. B. C. D.
8.如图,已知一渔船上的渔民在A处看见灯塔M在北偏东60°方向,这艘渔船以28海里/时的速度向正东方向航行,半小时后到达B处,在B处看见灯塔M在北偏东15°方向,此时灯塔M与渔船的距离是( )
A.7海里 B.14海里 C.7海里 D.14海里
9.如果一个直角三角形的两条边长分别为和,那么这个三角形的第三边长为( )
A. B. C. D.或
10.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=12,则下列关于S1、S2、S3的说法正确的是( )
A.S1=2 B.S2=3 C.S3=6 D.S1+S3=8
二、填空题
11.若一个直角三角形的两直角边长分别为6cm和8cm,则此直角三角形斜边是______cm.
12.如图,,点在上,于点,于点.若,,则的长为______.
13.如图,在ΔABC中,∠A=90°,∠B=30°,AD为中线,AD=1,则BC=____,AB=____.
14.如图,四边形中,,,过点C作于点E,连接,若,,,则的长为_______.
15.如图,在△ABC中,∠C=90°,AB=5,AC=4,∠B,∠C的平分线相交于点O,OM∥AB,ON∥AC分别与BC交于点M、N,则△OMN的周长为____.
三、解答题
16.如图,在中,,是的中点,,点为垂足,,,求的长.
17.《九章算术》卷九中记载:今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽,问索长几何?译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索(绳索头与地面接触)退行,在距木柱根部8尺处时绳索用尽,问绳索长是多少?
18.如图,,,,…分别表示各个三角形的面积,仔细观察,并认真分析各式,然后解答问题.
,;
,;
,;
……
(1)用含n(n是正整数)的式子表示和;
(2)若一个三角形的面积是,通过计算说明它是第几个三角形.
参考答案
1.D
【详解】解:∵,,,
∴,
∵,D是BC的中点,垂足为D,
∴BE=CE,
故选:D.
2.B
【详解】解:∵由勾股定理得:AC2+BC2=AB2,
∴S2+S3=S1,
∵S1+S2+S3=16,
∴2S1=16,
∴S1=8,
故选:B
3.B
【详解】解:该圆柱的侧面展开图,如下图所示,
根据两点之间线段最短,可知沿着侧面需要爬行的最短路径即为AB,
AB恰为一个矩形的对角线,该矩形的长为圆柱的底面周长的一半,
即长为24÷2=12,
宽为5,
∴AB==13,
即沿着侧面需要爬行的最短路径长为13.
故选:B.
4.C
【详解】解:如图,
由勾股定理得,正方形F的面积=正方形A的面积+正方形B的面积=32+62=45,
同理,正方形G的面积=正方形C的面积+正方形D的面积=22+32=13,
∴正方形E的面积=正方形F的面积+正方形G的面积=45+13=58,
故选:C.
5.C
【详解】当∠APB=90时,如图1,
∵AB=AC,BC=6,
∴BP=CP=BC=3;
∵∠B=30,
∴AB=2AP,
由勾股定理得:(2AP)2=AP2+32,
解得:AP=,AB=2AP=2,
当∠BAP=90,如图2,
∵∠B=30,
∴BP=2AP,
在Rt△ABP中,由勾股定理得:AB2+AP2=BP2,
(2)2+AP2=(2AP)2,
解得:AP=2,BP=2AP=4;
所以BP=3或4.
故选C.
6.B
【详解】解:如图,ABD是等腰三角形,ACD是等腰直角三角形,
∴AD=BD=n-m,
根据勾股定理得:m2+m2=(n m)2,
∴2m2=n2 2mn+m2,
m2+2mn n2=0.
故选:B.
7.A
【详解】解:∵BC=4a,
∴图①中,BE=a,图②中,BE=a,
∴小直角三角形的斜边长为,
∴图③中纸盒底部剩余部分CF的长为4a-2×a=a;
故选:A.
8.A
【详解】解:由已知得,AB=×28=14km,∠MAB=30°,∠ABM=105°.
过点B作BN⊥AM于点N.
∵在直角△ABN中,∠BAN=30°
∴BN=AB=7km.
在直角△BNM中,∠MBN=45°,
则直角△BNM是等腰直角三角形,
即BN=MN=7km,
∴BM===km.
故选:A.
9.D
【详解】解:当6和10是两条直角边时,
第三边=,
当6和10分别是一斜边和一直角边时,
第三边==8,
所以第三边可能为8或2.
故选:D.
10.D
【详解】解:八个直角三角形全等,四边形ABCD,EFGH,MNKT是正方形,
,,
,
,
,
,
,
,
,
,
,
,
故选:D.
11.10
【详解】解:由勾股定理得,直角三角形的斜边为cm.
故答案为:10
12..
【详解】因为∠AOC=∠BOC, 所以OC平分∠AOB又因为PD⊥OA,PE⊥OB,
所以PD=PE,
在直角三角形ODP中,OD=2,OP=3,所以由勾股定理得,
所以PE=,
故答案为:.
13.
【详解】解:∵在ΔABC中,∠A=90°,∠B=30°,
∴∠C=180°-∠CAB-∠B=180°-90°-30°=60°,BC=2AC,
∵AD为中线,
∴BD=CD=,
∴△DCA为等边三角形,
∵AD=1,
∴CD=AD=AC=1,
∴BC=2CD=2,
根据勾股定理AB=;
故答案为:2;.
14.
【详解】解:作DF⊥BC,DG⊥AB,
∵AD=CD,
∴∠DAC=∠DCA,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠CDE,
∵∠CDE=∠DAC+∠DCA=2∠DAC =∠CDE,
∴∠ABC=∠CDE=∠ACD
∴∠BAD=∠GAC-∠DAC=∠ABC+∠ACB-∠DAC=2∠DAC +2∠DAC -∠DAC =3∠DAC,
∵DA=DC,∠AGD=∠DFC,∠GAD=∠FCD,
∴,
∴DG=DF,
∴DB为∠ABC的角平分线,
∴∠ABD=,
作AH⊥BD,
∵AB=AC,∠ABH=∠EAC=∠DAC,∠AHB=∠CEA=90°,
∴,
∴AH=CE=,
∵∠AHD=∠BHC,∠HBC=∠HAD=∠DAC,
∴∠HAD=∠HCB=∠CDE,
∵AD=DC,∠HAD=∠HCB=∠CDE,∠AHD=∠E=90°,
∴,
∴HD=ED,
设BD=5x,AD=DC=2x,HD=ED=y,
由BH=AE得5x-y=2x+y,
∴,
在中,
,
∴x=2,
在中,AB=.
故答案为:.
15.
【详解】解:∵∠ACB=90°,AB=5,AC=4,
∴,
∵BO平分∠ABC,OM∥AB,
∴∠OBC=∠ABC,∠ABC=∠OMC,
又∵∠OMC=∠OBC+∠MOB,
∴∠OBC=∠MOB,
∴OM=MB,
同理可得ON=NC,
∴△OMN的周长=ON+NM+OM=NC+NM+MB=BC=3,
故答案为3.
16.
【详解】解:连接.设,
∵, ,
∴ , , ,
∴
,
∴.
故答案为.
17.
【详解】设绳索长为x尺
∴根据题意得:
解得.
∴绳索长为尺.
18.
【详解】(1),.
(2)当时,,即,
所以它是第20个三角形.
