长方体的体积(同步练习)-五年级下册数学北师大版(无答案)
文档属性
| 名称 | 长方体的体积(同步练习)-五年级下册数学北师大版(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 82.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-15 08:19:12 | ||
图片预览




文档简介
长正方体的体积(一)
【知识要点】
体积和容积的区别:
意义不同:体积表示物体所占空间的大小;容积表示容器所能容纳物体的体积;
测量方法不同:体积是从物体的外部测量;容积是从物体的内部测量;
同一个容器,体积大于容积,当容器壁很薄时,容积近似等于体积,容器壁忽略不计时,两者相等;
拓展:无论是几个物体拼合成一个物体或同一个物体切成几部分,它的表面积都会发生变化,但总体积不会发生变化;
体积单位:
(1)常用体积单位:厘米3、分米3和米3,用字母表示为cm3、dm3和m3;
常用容积单位:毫升和升,用字母表示:mL和L;
(2)容积与体积单位之间的联系:
1L=1 dm3 1mL= cm3 1L=1000mL
体积的计算:
长方体的体积=长×宽×高,用字母表示V=abh;
正方体的体积=棱长×棱长×棱长,用字母表示V=a3;
【经典习题】
习题1、体积和容积的认识:
(1)做一个汽油箱,要用多少铁皮,是求油箱的( );这个油箱占多大的空间是求油箱的( );油箱能装多少汽油是求油箱的( )。
A. 体积 B. 容积 C. 表面积
(2)一个壁厚为4厘米的木桶,它的容积( )体积。(填“大于”、“小于”或“等于”)
习题2、体积的变化情况:
(1)有一块彩泥,小方第一次把它捏成了长方体,第二次把它捏成了正方体,第三次把它捏成了一个不规则形体。这三次捏成的物体,哪一个体积最大?为什么?
(2)一个长12厘米、宽10厘米、高8厘米的长方体,截成两个形状、大小完全一样的长方体,表面积最少增加多少平方厘米?体积有变化吗?
习题3、体积单位:填上适当的单位名称:
(1)阿如买了一大桶饮料,净含量1.5( )
(2)一袋草莓酸奶约200 ( )
(3)一个文具盒的体积约是0.4( )
(4)教室里面空着的体积约是170( )
(5)小何家装修房子,拉了一汽车沙子,沙子约有12( )
习题4、体积的计算:
(1)一个正方体,棱长扩大3倍,则表面积扩大( ),体积扩大( )。
A.3倍 B.9倍 C.6倍 D.27倍
(2)从一个棱长为2米的大正方体的一个角上切掉一个棱长为2厘米的小正方体后,表面积比原来( ),体积比原来( )。
A.减少了 B.增多了 C.没有变 D.不能比较
(3)用一根24dm长的铁丝围成一个最大的正方体形状的框架,这个正方体的体积是( )dm3。
(4)把一块棱长为6cm的正方体橡皮泥,捏成长为9cm、宽为8cm的长方体,捏成的长方体的高是( )cm。
(5)娜娜在一个装有500mL水的玻璃杯中浸入一个苹果后,发现玻璃杯中的水上升到855mL,这个苹果的体积是( )立方厘米。
(6)1个长6cm、宽4cm、高8cm的长方体木块,能切成( )个棱长为2cm的小正方体木块。
(7)一个长方体的体积是54立方分米,底面积是15平方分米,高是( )分米
☆(8)有一块长方体木块,长14cm,宽9cm,高4cm,工人师傅想用它截成体积最大的正方体。截出的正方体体积是多少?能截成几个这样的正方体呢?
习题5、计算下面形体的体积。(单位:cm)
【巩固练习】
1、把5L水倒入长0.4m,宽0.2m的玻璃鱼缸中,水深( )dm。
2、一个正方体的表面积是96dm2,它的一个面的面积是( )dm2,体积是( )dm3。
3、一个长方体,正好可以切成两个棱长是3厘米的正方体,这个长方体的体积是( )。
4、一个棱长为16cm的正方体容器内水深8cm,浸入一个铁块后,水面上升到距容器口3cm处,这个铁块的体积是( )cm3。
5、如果长方体的长、宽、高都扩大到原来的5倍,那么它的体积扩大到原来的( )倍。
6、一个长方体的横截面是边长为3厘米的正方形,它的长是5厘米,体积是( )立方厘米。
7、判断:
(1)物体的体积越大,容积就越大。 ( )
(2)体积是1dm3的正方体的棱长一定是1dm。 ( )
(3)1分米3=1升,所以棱长是1分米的正方体的体积是1升。 ( )
(4)输液瓶里装满了500毫升的药液,输液瓶的容积是500毫升。 ( )
(5)两个体积相等的正方体,它们的棱长一定相等。 ( )
(6)棱长是6分米的正方体,它的表面积和体积相等。 ( )
8、把一个棱长是20厘米的正方体钢坯,锻造成底面为正方形的长方体钢材,底面边长是5厘米,这段钢材的高是多少米?
9、一根长方体木料,长2m,垂直于长的截面是边长是2dm的正方形,若每立方分米这种木料重0.6kg,那么这根木料重多少千克?
10、8个小正方体拼成的大正方体,从它的一角拿走一个小正方体,表面积有没有变化?体积呢?为什么?
11、棱长之和是60分米,长是7分米,高是3分米,求长方体体积。
【巩固加强】
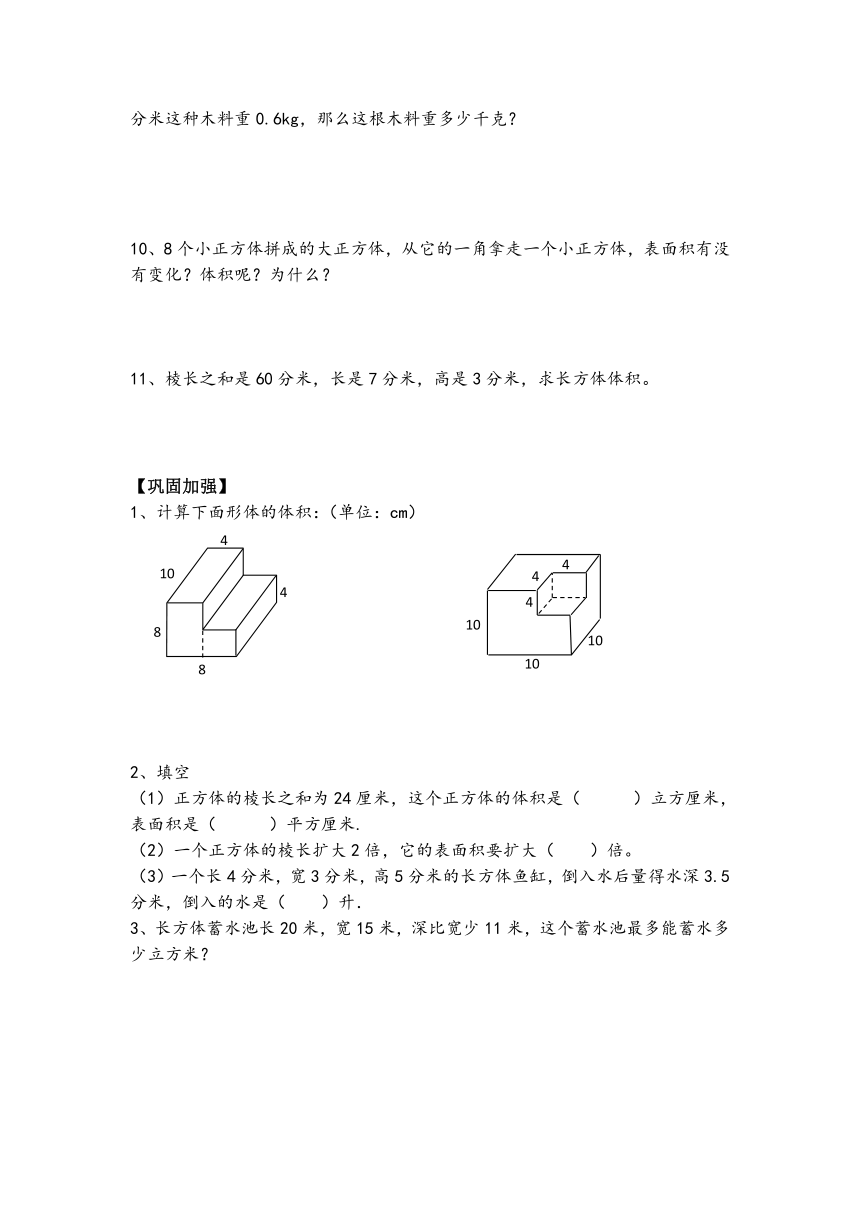
1、计算下面形体的体积:(单位:cm)
2、填空
(1)正方体的棱长之和为24厘米,这个正方体的体积是( )立方厘米,表面积是( )平方厘米.
(2)一个正方体的棱长扩大2倍,它的表面积要扩大( )倍。
(3)一个长4分米,宽3分米,高5分米的长方体鱼缸,倒入水后量得水深3.5分米,倒入的水是( )升.
3、长方体蓄水池长20米,宽15米,深比宽少11米,这个蓄水池最多能蓄水多少立方米?
4、有一个正方体水箱,棱长为4分米,装满一箱水后,倒入另一个长0.8米,宽25厘米的长方体水箱中,水深多少?
5、一个长12厘米,宽8厘米的容器里面装了一部分水,向其中丢入一个小铁块后,铁块完全浸没,水面上升5厘米.铁块的体积是多少立方厘米?
长正方体的体积复习
【知识要点】
长方体、正方体体积的统一计算公式:
长方体(正方体)的体积=底面积×高,字母公式为V=Sh(S表示底面积,h表示高);
拓展:长方体的体积=横截面积×长;
体积、容积单位之间的进率:
(1)1 dm3=1000 cm3 1 m3=1000 dm3 1L=1000mL
相邻体积、容积单位之间的进率为1000;
(2)容积与体积单位之间的联系:
1L=1 dm3 1mL=1cm3 1L=1000mL
不规则物体体积的测量:
在测量不规则物体的体积时,一般是把不规则物体的体积转化成可通过测量计算的水的体积。
排水法:先测量出原来水的体积,然后把物体放入容器,再测量水和物体的体积,最后用水和物体的体积减去原来水的体积就可以求出该物体的体积了。
【经典习题】
习题1、求体积(易混题):
红岭小学建一个长方体游泳池,长60米、宽2.5米、深2米。
游泳池占地面积是多少平方米?
在游泳池的底面和内壁抹一层水泥,抹水泥的面积是多少平方米?
沿游泳池的内壁1.5米高处用白漆画一条水位线,水位线全长是多少米?
按水位线进水,游泳池内共存水多少立方米?
习题2、一个长方体容器的长、宽、高分别是9分米、8分米、5分米。装满水后,倒入一个棱长为1米的正方体容器中,这时水深是多少分米?
习题3、把一根长3分米的长方体木料锯成相同的两段后,表面积比原来增加了96平方分米,这根木料原来的体积是多少?
习题4、一个长、宽、高分别为18分米、12分米、10分米的水槽中注入7分米深的水,然后放进一个棱长为6分米的正方体铁块。水位上升多少分米?
习题5、把一块不规则的石头放进一个底面积20平方分米,高5分米,水深2分米的长方体容器里,水上升到离上沿只有0.5分米处,这块石头的体积是多少立方分米?
【拓展提高】
习题6、一个长方体,若将它的长减少2厘米,就变成了一个正方体,这个正方体的表面积比原来长方体的表面积减少了56平方厘米。求原来长方体的体积。
习题7、一个正方体增高6厘米,就得到一个底面积不变的长方体,表面积增加了120平方厘米,原来正方体的体积是多少立方厘米?
习题8、把一根长2.4米的长方体木料锯成5段,表面积比原来增加了96平方厘米,这根木料原来的体积是多少立方厘米?
【巩固练习】
1、体积、容积单位之间的进率:
0.2m3=( )dm3=( )cm3 3000L=( )m3
500mL=( )L=( )dm3 2.8dm3=( )L=( )mL
5m350dm3=( )m3=( )dm3 2.08m2=( )m2( )dm2
2、1000个体积是1厘米3的小正方体堆成一个大正方体,大正方体的体积是( )分米3。
3、一个长方体,长0.7米、宽4分米、高2分米,它的体积是( )立方分米,合( )立方米。
4、一个长方体油箱的容积是2000毫升,这个油箱的内底长25厘米,宽20厘米,油箱深( )厘米。
5、长方体的底面积是80平方厘米,高是7分米,它的体积是( )立方厘米。
6、一块长方体木料的体积是1.08立方米,它的横截面面积是0.6平方米,它的高是( )米。
7、一个容器内盛满了1升水,将一个玻璃球没入水中,溢出了0.3升水,则玻璃球的体积是( )分米3。
8、一个体积为15dm3的铁块沉入到一个长5dm,宽2dm的长方体容器中,水面会上升( )dm。
9、有一个长方体容器,从里面量长5分米,宽4分米,高6分米,里面注了水,水深3分米。如果把一块棱长2分米的正方体铁块浸入水中,水面上升( )分米。
10、两个正方体拼在一起的体积(单位:厘米)
11、有一个正方体水箱,棱长为4分米,装满一箱水后,倒入另一个长0.8米,宽25厘米的长方体水箱中,水深多少?
12、把两块棱长相等的正方体拼成一个长方体,已知长方体的棱长总和是96厘米,则每个正方体的体积是多少立方厘米?
13、一个正方体的高增加3厘米,得到的新长方体的表面积比原来正方体的表面积增加了60平方厘米。求原来正方体的体积。
【强化训练】
1、判断:
(1)将100个棱长1cm的小正方体拼在一起,无论怎样拼,拼出的图形的体积都是100cm3。 ( )
(2)一个长方体的底面积不变,高扩大4倍,体积就扩大4倍。 ( )
(3)把体积是1立方米的纸盒放在地面上,它的占地面积一定是1平方米。 ( )
2、一个正方体水箱,棱长是8dm,里面装满了水,如果把这些水倒入另一个长8dm、宽5dm的长方体水箱中,水深是( )分米。
3、一个正方体玻璃容器,从里面量边长4分米,向容器中倒入25L水,再把一块石块放入水中,这时量得容器内的水深是2.5分米。这块石块的体积是( )立方分米。
4、在一个棱长是50厘米的正方体容器中注入3分米高的水,又投入1分米3的铅块,这时容器所装物体的体积是( )。
5、有一个长方体水箱,从里面量长12分米、宽10分米、高5分米。箱内水面离箱口1.5分米,箱内一共有水( )升。
6、长方体棱长之和是80分米,宽是8分米,高是7分米,求长方体体积?
7、一个长方体,如果高增加了3cm,就变成一个正方体,这时表面积比原来增加144cm2.原来长方体的体积是多少立方厘米?
【知识要点】
体积和容积的区别:
意义不同:体积表示物体所占空间的大小;容积表示容器所能容纳物体的体积;
测量方法不同:体积是从物体的外部测量;容积是从物体的内部测量;
同一个容器,体积大于容积,当容器壁很薄时,容积近似等于体积,容器壁忽略不计时,两者相等;
拓展:无论是几个物体拼合成一个物体或同一个物体切成几部分,它的表面积都会发生变化,但总体积不会发生变化;
体积单位:
(1)常用体积单位:厘米3、分米3和米3,用字母表示为cm3、dm3和m3;
常用容积单位:毫升和升,用字母表示:mL和L;
(2)容积与体积单位之间的联系:
1L=1 dm3 1mL= cm3 1L=1000mL
体积的计算:
长方体的体积=长×宽×高,用字母表示V=abh;
正方体的体积=棱长×棱长×棱长,用字母表示V=a3;
【经典习题】
习题1、体积和容积的认识:
(1)做一个汽油箱,要用多少铁皮,是求油箱的( );这个油箱占多大的空间是求油箱的( );油箱能装多少汽油是求油箱的( )。
A. 体积 B. 容积 C. 表面积
(2)一个壁厚为4厘米的木桶,它的容积( )体积。(填“大于”、“小于”或“等于”)
习题2、体积的变化情况:
(1)有一块彩泥,小方第一次把它捏成了长方体,第二次把它捏成了正方体,第三次把它捏成了一个不规则形体。这三次捏成的物体,哪一个体积最大?为什么?
(2)一个长12厘米、宽10厘米、高8厘米的长方体,截成两个形状、大小完全一样的长方体,表面积最少增加多少平方厘米?体积有变化吗?
习题3、体积单位:填上适当的单位名称:
(1)阿如买了一大桶饮料,净含量1.5( )
(2)一袋草莓酸奶约200 ( )
(3)一个文具盒的体积约是0.4( )
(4)教室里面空着的体积约是170( )
(5)小何家装修房子,拉了一汽车沙子,沙子约有12( )
习题4、体积的计算:
(1)一个正方体,棱长扩大3倍,则表面积扩大( ),体积扩大( )。
A.3倍 B.9倍 C.6倍 D.27倍
(2)从一个棱长为2米的大正方体的一个角上切掉一个棱长为2厘米的小正方体后,表面积比原来( ),体积比原来( )。
A.减少了 B.增多了 C.没有变 D.不能比较
(3)用一根24dm长的铁丝围成一个最大的正方体形状的框架,这个正方体的体积是( )dm3。
(4)把一块棱长为6cm的正方体橡皮泥,捏成长为9cm、宽为8cm的长方体,捏成的长方体的高是( )cm。
(5)娜娜在一个装有500mL水的玻璃杯中浸入一个苹果后,发现玻璃杯中的水上升到855mL,这个苹果的体积是( )立方厘米。
(6)1个长6cm、宽4cm、高8cm的长方体木块,能切成( )个棱长为2cm的小正方体木块。
(7)一个长方体的体积是54立方分米,底面积是15平方分米,高是( )分米
☆(8)有一块长方体木块,长14cm,宽9cm,高4cm,工人师傅想用它截成体积最大的正方体。截出的正方体体积是多少?能截成几个这样的正方体呢?
习题5、计算下面形体的体积。(单位:cm)
【巩固练习】
1、把5L水倒入长0.4m,宽0.2m的玻璃鱼缸中,水深( )dm。
2、一个正方体的表面积是96dm2,它的一个面的面积是( )dm2,体积是( )dm3。
3、一个长方体,正好可以切成两个棱长是3厘米的正方体,这个长方体的体积是( )。
4、一个棱长为16cm的正方体容器内水深8cm,浸入一个铁块后,水面上升到距容器口3cm处,这个铁块的体积是( )cm3。
5、如果长方体的长、宽、高都扩大到原来的5倍,那么它的体积扩大到原来的( )倍。
6、一个长方体的横截面是边长为3厘米的正方形,它的长是5厘米,体积是( )立方厘米。
7、判断:
(1)物体的体积越大,容积就越大。 ( )
(2)体积是1dm3的正方体的棱长一定是1dm。 ( )
(3)1分米3=1升,所以棱长是1分米的正方体的体积是1升。 ( )
(4)输液瓶里装满了500毫升的药液,输液瓶的容积是500毫升。 ( )
(5)两个体积相等的正方体,它们的棱长一定相等。 ( )
(6)棱长是6分米的正方体,它的表面积和体积相等。 ( )
8、把一个棱长是20厘米的正方体钢坯,锻造成底面为正方形的长方体钢材,底面边长是5厘米,这段钢材的高是多少米?
9、一根长方体木料,长2m,垂直于长的截面是边长是2dm的正方形,若每立方分米这种木料重0.6kg,那么这根木料重多少千克?
10、8个小正方体拼成的大正方体,从它的一角拿走一个小正方体,表面积有没有变化?体积呢?为什么?
11、棱长之和是60分米,长是7分米,高是3分米,求长方体体积。
【巩固加强】
1、计算下面形体的体积:(单位:cm)
2、填空
(1)正方体的棱长之和为24厘米,这个正方体的体积是( )立方厘米,表面积是( )平方厘米.
(2)一个正方体的棱长扩大2倍,它的表面积要扩大( )倍。
(3)一个长4分米,宽3分米,高5分米的长方体鱼缸,倒入水后量得水深3.5分米,倒入的水是( )升.
3、长方体蓄水池长20米,宽15米,深比宽少11米,这个蓄水池最多能蓄水多少立方米?
4、有一个正方体水箱,棱长为4分米,装满一箱水后,倒入另一个长0.8米,宽25厘米的长方体水箱中,水深多少?
5、一个长12厘米,宽8厘米的容器里面装了一部分水,向其中丢入一个小铁块后,铁块完全浸没,水面上升5厘米.铁块的体积是多少立方厘米?
长正方体的体积复习
【知识要点】
长方体、正方体体积的统一计算公式:
长方体(正方体)的体积=底面积×高,字母公式为V=Sh(S表示底面积,h表示高);
拓展:长方体的体积=横截面积×长;
体积、容积单位之间的进率:
(1)1 dm3=1000 cm3 1 m3=1000 dm3 1L=1000mL
相邻体积、容积单位之间的进率为1000;
(2)容积与体积单位之间的联系:
1L=1 dm3 1mL=1cm3 1L=1000mL
不规则物体体积的测量:
在测量不规则物体的体积时,一般是把不规则物体的体积转化成可通过测量计算的水的体积。
排水法:先测量出原来水的体积,然后把物体放入容器,再测量水和物体的体积,最后用水和物体的体积减去原来水的体积就可以求出该物体的体积了。
【经典习题】
习题1、求体积(易混题):
红岭小学建一个长方体游泳池,长60米、宽2.5米、深2米。
游泳池占地面积是多少平方米?
在游泳池的底面和内壁抹一层水泥,抹水泥的面积是多少平方米?
沿游泳池的内壁1.5米高处用白漆画一条水位线,水位线全长是多少米?
按水位线进水,游泳池内共存水多少立方米?
习题2、一个长方体容器的长、宽、高分别是9分米、8分米、5分米。装满水后,倒入一个棱长为1米的正方体容器中,这时水深是多少分米?
习题3、把一根长3分米的长方体木料锯成相同的两段后,表面积比原来增加了96平方分米,这根木料原来的体积是多少?
习题4、一个长、宽、高分别为18分米、12分米、10分米的水槽中注入7分米深的水,然后放进一个棱长为6分米的正方体铁块。水位上升多少分米?
习题5、把一块不规则的石头放进一个底面积20平方分米,高5分米,水深2分米的长方体容器里,水上升到离上沿只有0.5分米处,这块石头的体积是多少立方分米?
【拓展提高】
习题6、一个长方体,若将它的长减少2厘米,就变成了一个正方体,这个正方体的表面积比原来长方体的表面积减少了56平方厘米。求原来长方体的体积。
习题7、一个正方体增高6厘米,就得到一个底面积不变的长方体,表面积增加了120平方厘米,原来正方体的体积是多少立方厘米?
习题8、把一根长2.4米的长方体木料锯成5段,表面积比原来增加了96平方厘米,这根木料原来的体积是多少立方厘米?
【巩固练习】
1、体积、容积单位之间的进率:
0.2m3=( )dm3=( )cm3 3000L=( )m3
500mL=( )L=( )dm3 2.8dm3=( )L=( )mL
5m350dm3=( )m3=( )dm3 2.08m2=( )m2( )dm2
2、1000个体积是1厘米3的小正方体堆成一个大正方体,大正方体的体积是( )分米3。
3、一个长方体,长0.7米、宽4分米、高2分米,它的体积是( )立方分米,合( )立方米。
4、一个长方体油箱的容积是2000毫升,这个油箱的内底长25厘米,宽20厘米,油箱深( )厘米。
5、长方体的底面积是80平方厘米,高是7分米,它的体积是( )立方厘米。
6、一块长方体木料的体积是1.08立方米,它的横截面面积是0.6平方米,它的高是( )米。
7、一个容器内盛满了1升水,将一个玻璃球没入水中,溢出了0.3升水,则玻璃球的体积是( )分米3。
8、一个体积为15dm3的铁块沉入到一个长5dm,宽2dm的长方体容器中,水面会上升( )dm。
9、有一个长方体容器,从里面量长5分米,宽4分米,高6分米,里面注了水,水深3分米。如果把一块棱长2分米的正方体铁块浸入水中,水面上升( )分米。
10、两个正方体拼在一起的体积(单位:厘米)
11、有一个正方体水箱,棱长为4分米,装满一箱水后,倒入另一个长0.8米,宽25厘米的长方体水箱中,水深多少?
12、把两块棱长相等的正方体拼成一个长方体,已知长方体的棱长总和是96厘米,则每个正方体的体积是多少立方厘米?
13、一个正方体的高增加3厘米,得到的新长方体的表面积比原来正方体的表面积增加了60平方厘米。求原来正方体的体积。
【强化训练】
1、判断:
(1)将100个棱长1cm的小正方体拼在一起,无论怎样拼,拼出的图形的体积都是100cm3。 ( )
(2)一个长方体的底面积不变,高扩大4倍,体积就扩大4倍。 ( )
(3)把体积是1立方米的纸盒放在地面上,它的占地面积一定是1平方米。 ( )
2、一个正方体水箱,棱长是8dm,里面装满了水,如果把这些水倒入另一个长8dm、宽5dm的长方体水箱中,水深是( )分米。
3、一个正方体玻璃容器,从里面量边长4分米,向容器中倒入25L水,再把一块石块放入水中,这时量得容器内的水深是2.5分米。这块石块的体积是( )立方分米。
4、在一个棱长是50厘米的正方体容器中注入3分米高的水,又投入1分米3的铅块,这时容器所装物体的体积是( )。
5、有一个长方体水箱,从里面量长12分米、宽10分米、高5分米。箱内水面离箱口1.5分米,箱内一共有水( )升。
6、长方体棱长之和是80分米,宽是8分米,高是7分米,求长方体体积?
7、一个长方体,如果高增加了3cm,就变成一个正方体,这时表面积比原来增加144cm2.原来长方体的体积是多少立方厘米?
