2022-2023年华东师大版九年级数学下册 26.3 二次函数实践与探索课后综合练习 (无答案)
文档属性
| 名称 | 2022-2023年华东师大版九年级数学下册 26.3 二次函数实践与探索课后综合练习 (无答案) | 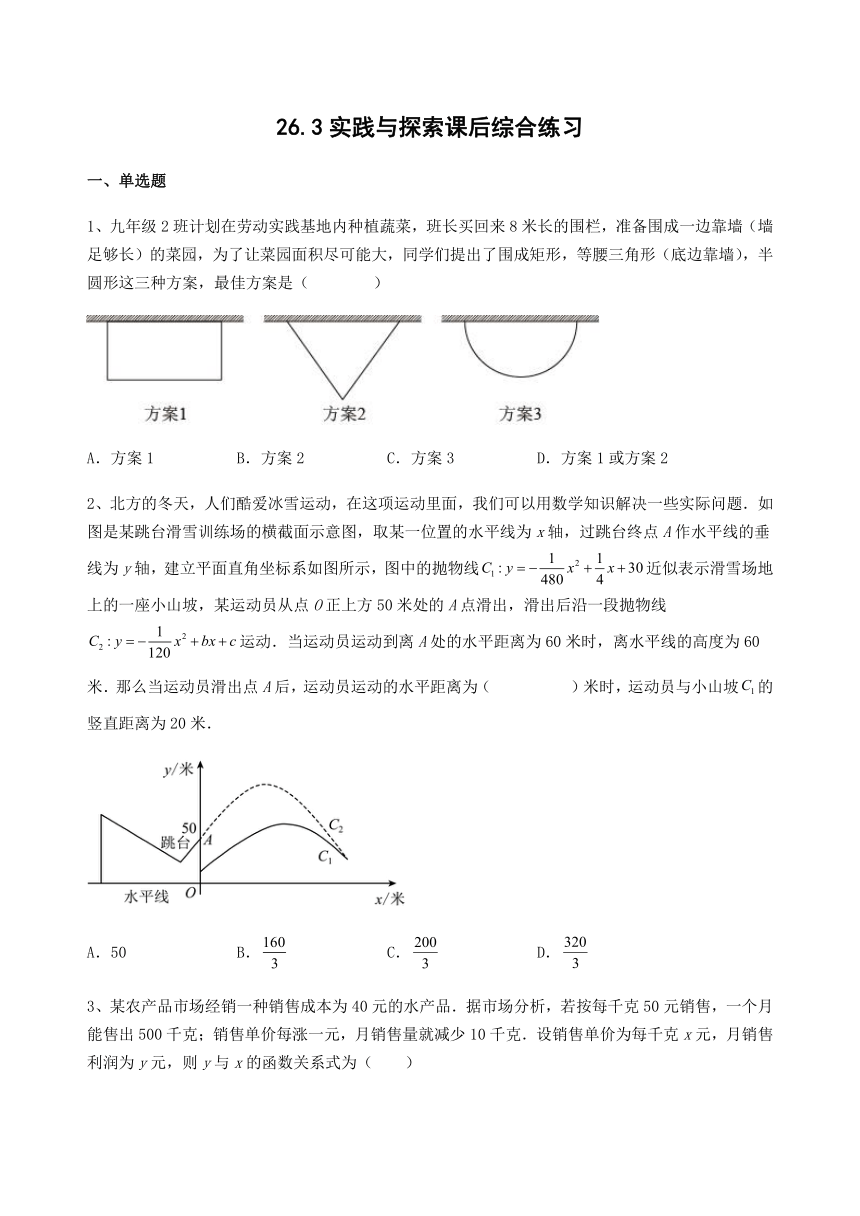 | |
| 格式 | docx | ||
| 文件大小 | 522.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-16 08:37:29 | ||
图片预览




文档简介
26.3实践与探索课后综合练习
一、单选题
1、九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形,等腰三角形(底边靠墙),半圆形这三种方案,最佳方案是( )
A.方案1 B.方案2 C.方案3 D.方案1或方案2
2、北方的冬天,人们酷爱冰雪运动,在这项运动里面,我们可以用数学知识解决一些实际问题.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系如图所示,图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点O正上方50米处的A点滑出,滑出后沿一段抛物线运动.当运动员运动到离A处的水平距离为60米时,离水平线的高度为60米.那么当运动员滑出点A后,运动员运动的水平距离为( )米时,运动员与小山坡的竖直距离为20米.
A.50 B. C. D.
3、某农产品市场经销一种销售成本为40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨一元,月销售量就减少10千克.设销售单价为每千克x元,月销售利润为y元,则y与x的函数关系式为( )
A.y=(x﹣40)(500﹣10x) B.y=(x﹣40)(10x﹣500)
C.y=(x﹣40)[500﹣10(x﹣50)] D.y=(x﹣40)[500﹣10(50﹣x)]
4、某产品进货单价为90元,按100元一件出售时能售出500件.若每件涨价1元,则销售量就减少10件.则该产品能获得的最大利润为( )
A.5000元 B.8000元 C.9000元 D.10000元
5、如图,中,,,,动点P沿折线运动,到点B停止,动点Q沿运动到点C停止,点P运动速度为2cm/s,点Q的运动速度为2.5cm/s,设运动时间为,的面积为S,则S与对应关系的的图象大致是( ).
B.
C. D.
6、从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.则下列结论不正确的是( )
A.小球在空中经过的路程是40m B.小球运动的时间为6s
C.小球抛出3s时,速度为0 D.当s时,小球的高度m
7、某宾馆共有80间客房.宾馆负责人根据经验作出预测:今年7月份,每天的房间空闲数y(间)与定价x(元/间)之间满足y=x﹣42(x≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为( )
A.252元/间 B.256元/间 C.258元/间 D.260元/间
8、如图,一小球从斜坡点处抛出,球的抛出路线可以用二次函数刻画,斜坡可以用一次函数刻画.则下列结论错误的是( )
A.当小球达到最高处时,它离斜坡的竖直距离是
B.当小球落在斜坡上时,它离点的水平距离是
C.小球在运行过程中,它离斜坡的最大竖直距离是
D.该斜坡的坡度是:
二、填空题
1、如图,矩形中,,,点从点出发,沿边向点以1cm/s的速度移动;点从点出发,沿边向点以2cm/s的速度移动.,同时出发,分别到,后停止移动,则的最小面积是______.
2、如图,点A、B的坐标分别为 和 ,抛物线的顶点在线段上,与轴交于,两点(在的左侧),点的横坐标最小值为,则点D的横坐标的最大值为____.
3、如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端点安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为,水柱落地处离池中心距离为,则水管的长度是________.
4、如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.则S与x的函数关系式为_____________;花圃面积最大是____________平方米.
5、某商场要经营一种新上市的文具,进价为元,试营销阶段发现:当销售单价是元时,每天的销售量为件,销售单价每上涨1元,每天的销售量就减少件,当销售单价为_____元时,该文具每天的销售利润最大.
6、某公司经过市场调查,整理出某种商品在某个月的第x天与日销售量的相关信息如下表所示.已知商品的进价为20元/件,设该商品的日销售利润为y元.
第x天 售价(元/件) 日销售量件
(1)y与x的函数解析式为_______________;
(2)日销售的最大利润为_________元.
三、解答题
1、某厂家生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本(单位:元)、销售价(单位:元)与产量x(单位:千克)之间的函数关系.
(1)求折线ABD所表示的,与x之间的函数表达式.
(2)若产品产量不超过70千克,求产量x为多少千克时,获得的利润最大?最大利润是多少?
2、某乡镇贸易公司开设了一家网店,销售当地某种农产品,已知该农产品成本为每千克10元,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中10(1)写出y与x之间的函数关系式及自变量的取值范围;
(2)当销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
3、为推进“书香社区”建设,某社区计划购进一批图书.已知购买2本科技类图书和3本文学类图书需154元,购买4本科技类图书和5本文学类图书需282元.
(1)科技类图书与文学类图书的单价分别为多少元?
(2)为了支持“书香社区”建设,助推科技发展,商家对科技类图书推出销售优惠活动(文学类图书售价不变):购买科技类图书超过40本但不超过50本时,每增加1本,单价降低1元;超过50本时,均按购买50本时的单价销售.社区计划购进两种图书共计100本,其中科技类图书不少于30本,但不超过60本.按此优惠,社区至少要准备多少购书款?
4、某工厂生产并销售A,B两种型号车床共14台,生产并销售1台A型车床可以获利10万元;如果生产并销售不超过4台B型车床,则每台B型车床可以获利17万元,如果超出4台B型车床,则每超出1台,每台B型车床获利将均减少1万元.设生产并销售B型车床台.
(1)当时,完成以下两个问题:
①请补全下面的表格:
A型 B型
车床数量/台 ________
每台车床获利/万元 10 ________
②若生产并销售B型车床比生产并销售A型车床获得的利润多70万元,问:生产并销售B型车床多少台?
(2)当0<≤14时,设生产并销售A,B两种型号车床获得的总利润为W万元,如何分配生产并销售A,B两种车床的数量,使获得的总利润W最大?并求出最大利润.
5、如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的,正常水位时,大孔水面宽度为,顶点距水面,小孔顶点距水面.当水位上涨刚好淹没小孔时,求大孔的水面宽度.
一、单选题
1、九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形,等腰三角形(底边靠墙),半圆形这三种方案,最佳方案是( )
A.方案1 B.方案2 C.方案3 D.方案1或方案2
2、北方的冬天,人们酷爱冰雪运动,在这项运动里面,我们可以用数学知识解决一些实际问题.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系如图所示,图中的抛物线近似表示滑雪场地上的一座小山坡,某运动员从点O正上方50米处的A点滑出,滑出后沿一段抛物线运动.当运动员运动到离A处的水平距离为60米时,离水平线的高度为60米.那么当运动员滑出点A后,运动员运动的水平距离为( )米时,运动员与小山坡的竖直距离为20米.
A.50 B. C. D.
3、某农产品市场经销一种销售成本为40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨一元,月销售量就减少10千克.设销售单价为每千克x元,月销售利润为y元,则y与x的函数关系式为( )
A.y=(x﹣40)(500﹣10x) B.y=(x﹣40)(10x﹣500)
C.y=(x﹣40)[500﹣10(x﹣50)] D.y=(x﹣40)[500﹣10(50﹣x)]
4、某产品进货单价为90元,按100元一件出售时能售出500件.若每件涨价1元,则销售量就减少10件.则该产品能获得的最大利润为( )
A.5000元 B.8000元 C.9000元 D.10000元
5、如图,中,,,,动点P沿折线运动,到点B停止,动点Q沿运动到点C停止,点P运动速度为2cm/s,点Q的运动速度为2.5cm/s,设运动时间为,的面积为S,则S与对应关系的的图象大致是( ).
B.
C. D.
6、从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.则下列结论不正确的是( )
A.小球在空中经过的路程是40m B.小球运动的时间为6s
C.小球抛出3s时,速度为0 D.当s时,小球的高度m
7、某宾馆共有80间客房.宾馆负责人根据经验作出预测:今年7月份,每天的房间空闲数y(间)与定价x(元/间)之间满足y=x﹣42(x≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为( )
A.252元/间 B.256元/间 C.258元/间 D.260元/间
8、如图,一小球从斜坡点处抛出,球的抛出路线可以用二次函数刻画,斜坡可以用一次函数刻画.则下列结论错误的是( )
A.当小球达到最高处时,它离斜坡的竖直距离是
B.当小球落在斜坡上时,它离点的水平距离是
C.小球在运行过程中,它离斜坡的最大竖直距离是
D.该斜坡的坡度是:
二、填空题
1、如图,矩形中,,,点从点出发,沿边向点以1cm/s的速度移动;点从点出发,沿边向点以2cm/s的速度移动.,同时出发,分别到,后停止移动,则的最小面积是______.
2、如图,点A、B的坐标分别为 和 ,抛物线的顶点在线段上,与轴交于,两点(在的左侧),点的横坐标最小值为,则点D的横坐标的最大值为____.
3、如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端点安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为,水柱落地处离池中心距离为,则水管的长度是________.
4、如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.则S与x的函数关系式为_____________;花圃面积最大是____________平方米.
5、某商场要经营一种新上市的文具,进价为元,试营销阶段发现:当销售单价是元时,每天的销售量为件,销售单价每上涨1元,每天的销售量就减少件,当销售单价为_____元时,该文具每天的销售利润最大.
6、某公司经过市场调查,整理出某种商品在某个月的第x天与日销售量的相关信息如下表所示.已知商品的进价为20元/件,设该商品的日销售利润为y元.
第x天 售价(元/件) 日销售量件
(1)y与x的函数解析式为_______________;
(2)日销售的最大利润为_________元.
三、解答题
1、某厂家生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本(单位:元)、销售价(单位:元)与产量x(单位:千克)之间的函数关系.
(1)求折线ABD所表示的,与x之间的函数表达式.
(2)若产品产量不超过70千克,求产量x为多少千克时,获得的利润最大?最大利润是多少?
2、某乡镇贸易公司开设了一家网店,销售当地某种农产品,已知该农产品成本为每千克10元,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中10
(2)当销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
3、为推进“书香社区”建设,某社区计划购进一批图书.已知购买2本科技类图书和3本文学类图书需154元,购买4本科技类图书和5本文学类图书需282元.
(1)科技类图书与文学类图书的单价分别为多少元?
(2)为了支持“书香社区”建设,助推科技发展,商家对科技类图书推出销售优惠活动(文学类图书售价不变):购买科技类图书超过40本但不超过50本时,每增加1本,单价降低1元;超过50本时,均按购买50本时的单价销售.社区计划购进两种图书共计100本,其中科技类图书不少于30本,但不超过60本.按此优惠,社区至少要准备多少购书款?
4、某工厂生产并销售A,B两种型号车床共14台,生产并销售1台A型车床可以获利10万元;如果生产并销售不超过4台B型车床,则每台B型车床可以获利17万元,如果超出4台B型车床,则每超出1台,每台B型车床获利将均减少1万元.设生产并销售B型车床台.
(1)当时,完成以下两个问题:
①请补全下面的表格:
A型 B型
车床数量/台 ________
每台车床获利/万元 10 ________
②若生产并销售B型车床比生产并销售A型车床获得的利润多70万元,问:生产并销售B型车床多少台?
(2)当0<≤14时,设生产并销售A,B两种型号车床获得的总利润为W万元,如何分配生产并销售A,B两种车床的数量,使获得的总利润W最大?并求出最大利润.
5、如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的,正常水位时,大孔水面宽度为,顶点距水面,小孔顶点距水面.当水位上涨刚好淹没小孔时,求大孔的水面宽度.
