2022—2023学年人教版数学九年级下册 28.2 解直角三角形及其应用作业题 (无答案)
文档属性
| 名称 | 2022—2023学年人教版数学九年级下册 28.2 解直角三角形及其应用作业题 (无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 372.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-16 08:41:21 | ||
图片预览


文档简介
28.2 解直角三角形及其应用(作业题)-人教版九年级下册
一.选择题
.如图,在△ABC中,∠BAC=60°,BC=6,AD平分∠BAC交BC于点D( )
A.6 B.12 C.6 D.6
.在平面直角坐标系xOy中,已知点P(3,1)与原点O的连线与x轴的正半轴的夹角为α(0°<α<90°)( )
A.3 B. C. D.
.如图,小明在P处测得A处的俯角为15°,B处的俯角为60°,∠PHB=∠AFB=90°,若斜面AB坡度为1:( )
A.10m B.20m C.30m D.40m
.如图,在量角器的圆心O处下挂一铅锤,制作了一个简易测倾仪.量角器的0刻度线AB对准楼顶时,则此时观察楼顶的仰角度数是( )
A.40° B.50° C.130° D.140°
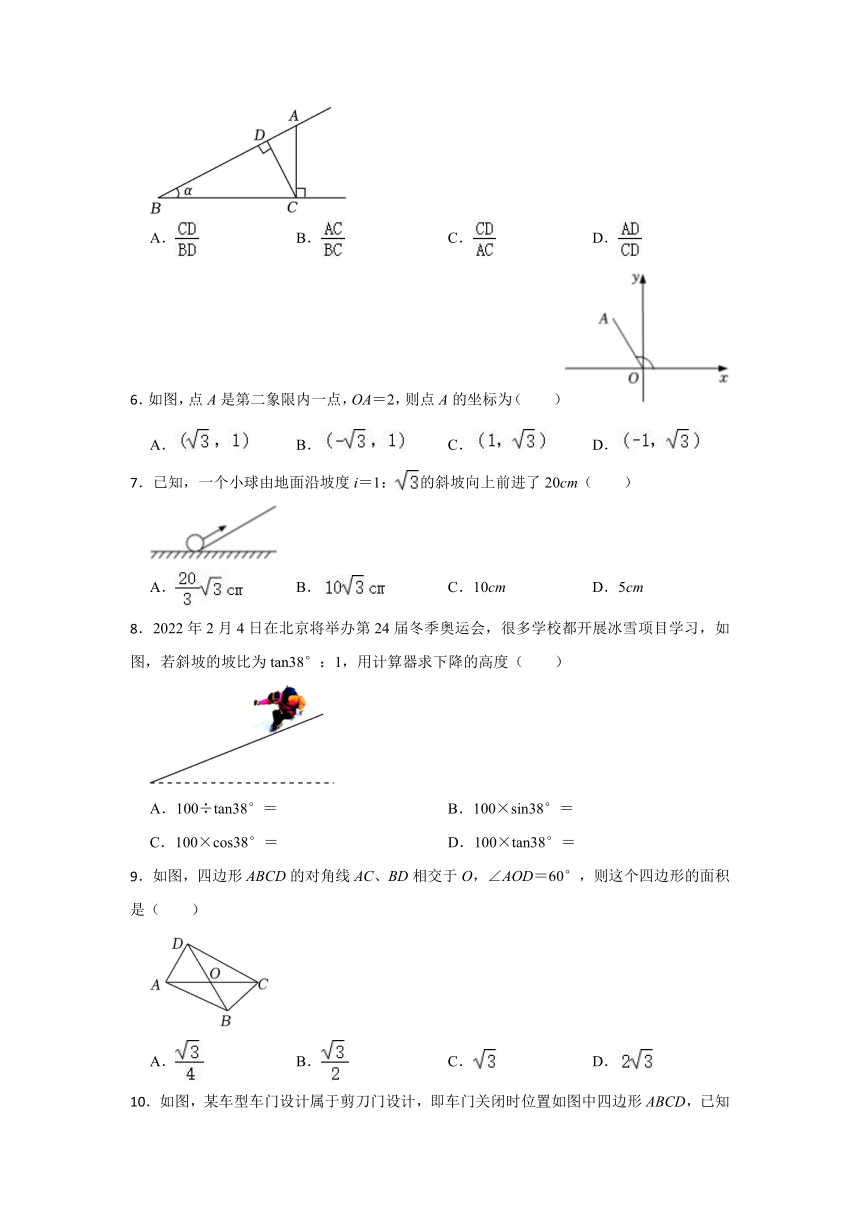
.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,下列用线段比表示tanα的值,错误的是( )
A. B. C. D.
.如图,点A是第二象限内一点,OA=2,则点A的坐标为( )
A. B. C. D.
.已知,一个小球由地面沿坡度i=1:的斜坡向上前进了20cm( )
A. B. C.10cm D.5cm
.2022年2月4日在北京将举办第24届冬季奥运会,很多学校都开展冰雪项目学习,如图,若斜坡的坡比为tan38°:1,用计算器求下降的高度( )
A.100÷tan38°= B.100×sin38°=
C.100×cos38°= D.100×tan38°=
.如图,四边形ABCD的对角线AC、BD相交于O,∠AOD=60°,则这个四边形的面积是( )
A. B. C. D.
.如图,某车型车门设计属于剪刀门设计,即车门关闭时位置如图中四边形ABCD,已知四边形ABCD与四边形AB'C'D'在同一平面,若AD∥BC,∠DAB'=30°,CD=60cm,( )
A.60cm B.51cm C.42cm D.21cm
二.填空题
.某人在斜坡走了10m,垂直高度上升8m,则坡比i= .
.平面直角坐标系内有一点P(1,2),那么OP与x轴正半轴的夹角为α,tanα= .
.如图,在Rt△ABC中,∠C=90°,BC=2,则∠A= °,AB= .
.如图,图中提供了一种求cot15°的方法.作 Rt△ABC,使∠C=90°,再延长CB到点D,使BD=BA,即可得∠D=15°.如果设AC=t,则可得CD=(2+)t=2+.用以上方法 .
.如图是某景区登山路线示意图,其中AD是缆车游览路线,折线A﹣B﹣C﹣D是登山步道,步道CD与水平面的夹角β为45°,BC是半山观景平台,CD=450m,缆车路线AD=1000m.其中点A,B,C,D,DE⊥AE.
(1)求点B到水平面AE的距离为 m;(不要带单位)
(2)求半山观景平台BC的长度 m.(结果保留整数)(参考数据:≈1.414,≈1.732)(不要带单位)
三.解答题
.如图是某货站传送货物的平面示意图.为了提高传送过程的安全性.工人师傅欲减小传送带与地面的夹角,使其由45°改为30°,已知原传送带AB长为4米.(说明,(1)(2),)
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走.并说明理由.
.同学们,在我们进入高中以后,还将学到下面三角函数公式:
sin(α﹣β)=sinαcosβ﹣cosαsinβ,sin(α+β),
cos(α﹣β)=cosαcosβ+sinαsinβ,cos(α+β)
例:sin15°=sin(45°﹣30°)=sin45℃os30°﹣cos45°sin30°=
(1)试仿照例题,求出cos75°的值;
(2)若已知锐角α满足条件sinα=,求sin2α的值.
.知识再现:如图1,在Rt△ABC中,∠C=90°,∠B,∠C的对边分别为a,b
∵,,
∴,.
∴.
(1)拓展探究:如图2,在锐角ABC中,∠A,∠C的对边分别为a,b,c.请探究,,,并写出探究过程.
(2)解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,∠A=75°,∠C=60°.请用拓展探究中的结论
.小明周末与父母一起到眉山湿地公园进行数学实践活动,在A处看到B,C处各有一棵被湖水隔开的银杏树.他在A处测得B在西北方向,又在B处测得C在北偏东60°方向.
(1)求∠C的度数;
(2)求两棵银杏树B,C之间的距离.(结果保留根号)
.如图,在平面直角坐标系中,O为坐标原点(20,0),点M在第一象限内,且OM=10.
(1)求点M的坐标.
(2)求cos∠MON的值.
一.选择题
.如图,在△ABC中,∠BAC=60°,BC=6,AD平分∠BAC交BC于点D( )
A.6 B.12 C.6 D.6
.在平面直角坐标系xOy中,已知点P(3,1)与原点O的连线与x轴的正半轴的夹角为α(0°<α<90°)( )
A.3 B. C. D.
.如图,小明在P处测得A处的俯角为15°,B处的俯角为60°,∠PHB=∠AFB=90°,若斜面AB坡度为1:( )
A.10m B.20m C.30m D.40m
.如图,在量角器的圆心O处下挂一铅锤,制作了一个简易测倾仪.量角器的0刻度线AB对准楼顶时,则此时观察楼顶的仰角度数是( )
A.40° B.50° C.130° D.140°
.如图,点A为∠α边上的任意一点,作AC⊥BC于点C,下列用线段比表示tanα的值,错误的是( )
A. B. C. D.
.如图,点A是第二象限内一点,OA=2,则点A的坐标为( )
A. B. C. D.
.已知,一个小球由地面沿坡度i=1:的斜坡向上前进了20cm( )
A. B. C.10cm D.5cm
.2022年2月4日在北京将举办第24届冬季奥运会,很多学校都开展冰雪项目学习,如图,若斜坡的坡比为tan38°:1,用计算器求下降的高度( )
A.100÷tan38°= B.100×sin38°=
C.100×cos38°= D.100×tan38°=
.如图,四边形ABCD的对角线AC、BD相交于O,∠AOD=60°,则这个四边形的面积是( )
A. B. C. D.
.如图,某车型车门设计属于剪刀门设计,即车门关闭时位置如图中四边形ABCD,已知四边形ABCD与四边形AB'C'D'在同一平面,若AD∥BC,∠DAB'=30°,CD=60cm,( )
A.60cm B.51cm C.42cm D.21cm
二.填空题
.某人在斜坡走了10m,垂直高度上升8m,则坡比i= .
.平面直角坐标系内有一点P(1,2),那么OP与x轴正半轴的夹角为α,tanα= .
.如图,在Rt△ABC中,∠C=90°,BC=2,则∠A= °,AB= .
.如图,图中提供了一种求cot15°的方法.作 Rt△ABC,使∠C=90°,再延长CB到点D,使BD=BA,即可得∠D=15°.如果设AC=t,则可得CD=(2+)t=2+.用以上方法 .
.如图是某景区登山路线示意图,其中AD是缆车游览路线,折线A﹣B﹣C﹣D是登山步道,步道CD与水平面的夹角β为45°,BC是半山观景平台,CD=450m,缆车路线AD=1000m.其中点A,B,C,D,DE⊥AE.
(1)求点B到水平面AE的距离为 m;(不要带单位)
(2)求半山观景平台BC的长度 m.(结果保留整数)(参考数据:≈1.414,≈1.732)(不要带单位)
三.解答题
.如图是某货站传送货物的平面示意图.为了提高传送过程的安全性.工人师傅欲减小传送带与地面的夹角,使其由45°改为30°,已知原传送带AB长为4米.(说明,(1)(2),)
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走.并说明理由.
.同学们,在我们进入高中以后,还将学到下面三角函数公式:
sin(α﹣β)=sinαcosβ﹣cosαsinβ,sin(α+β),
cos(α﹣β)=cosαcosβ+sinαsinβ,cos(α+β)
例:sin15°=sin(45°﹣30°)=sin45℃os30°﹣cos45°sin30°=
(1)试仿照例题,求出cos75°的值;
(2)若已知锐角α满足条件sinα=,求sin2α的值.
.知识再现:如图1,在Rt△ABC中,∠C=90°,∠B,∠C的对边分别为a,b
∵,,
∴,.
∴.
(1)拓展探究:如图2,在锐角ABC中,∠A,∠C的对边分别为a,b,c.请探究,,,并写出探究过程.
(2)解决问题:如图3,为测量点A到河对岸点B的距离,选取与点A在河岸同一侧的点C,∠A=75°,∠C=60°.请用拓展探究中的结论
.小明周末与父母一起到眉山湿地公园进行数学实践活动,在A处看到B,C处各有一棵被湖水隔开的银杏树.他在A处测得B在西北方向,又在B处测得C在北偏东60°方向.
(1)求∠C的度数;
(2)求两棵银杏树B,C之间的距离.(结果保留根号)
.如图,在平面直角坐标系中,O为坐标原点(20,0),点M在第一象限内,且OM=10.
(1)求点M的坐标.
(2)求cos∠MON的值.
