18.1 变量与函数[下学期]

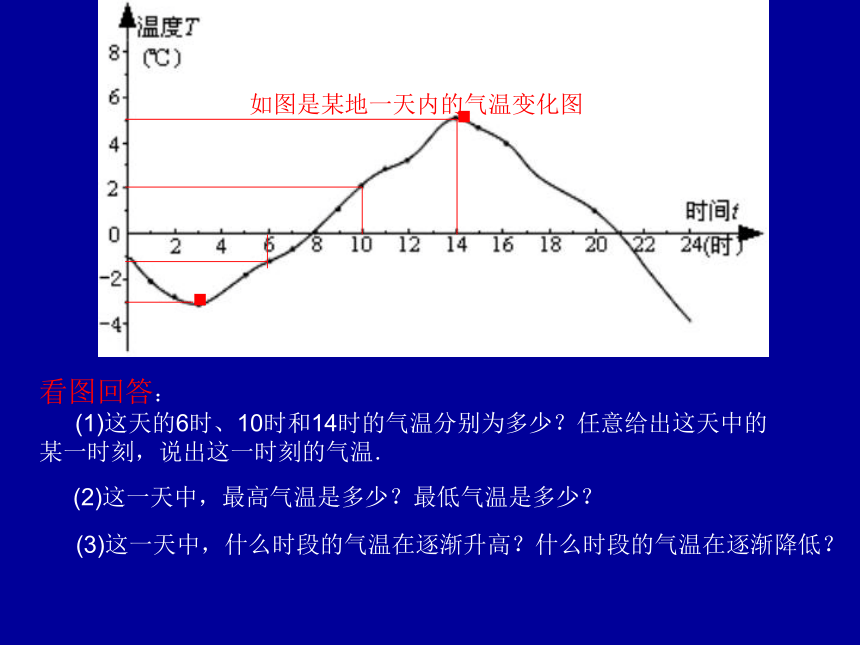
课件10张PPT。变量与函数第一课时如图是某地一天内的气温变化图 看图回答：
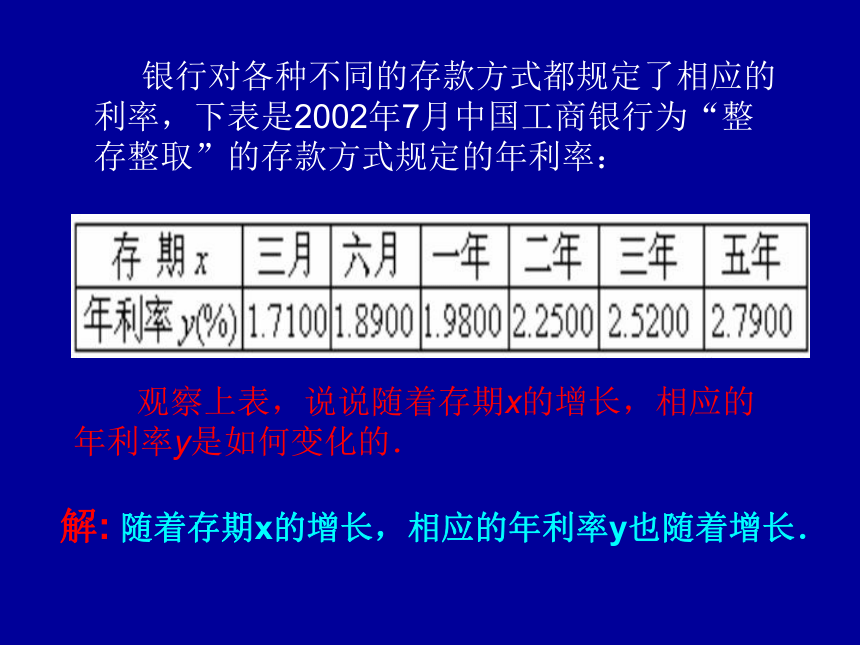
(1)这天的6时、10时和14时的气温分别为多少？任意给出这天中的某一时刻，说出这一时刻的气温．(2)这一天中，最高气温是多少？最低气温是多少？(3)这一天中，什么时段的气温在逐渐升高？什么时段的气温在逐渐降低？ ·· 银行对各种不同的存款方式都规定了相应的利率，下表是2002年7月中国工商银行为“整存整取”的存款方式规定的年利率： 观察上表，说说随着存期x的增长，相应的年利率y是如何变化的．解: 随着存期x的增长，相应的年利率y也随着增长． 收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的．下面是一些对应的数值： 观察上表回答：
(1)波长l和频率f数值之间有什么关系?
(2)波长l越大，频率f 就________．解 :(1) l 与 f 的乘积是一个定值，即lf＝300 000，或者说 (2)波长l越大，频率f 就越小　． 在上面的问题中，我们研究了一些数量关系，它们都刻画了某些变化规律．这里出现了各种各样的量，特别值得注意的是出现了一些数值会发生变化的量．例如问题1中，刻画气温变化规律的量是时间t和气温T，气温T随着时间t的变化而变化，它们都会取不同的数值．像这样在某一变化过程中，可以取不同数值的量，叫做变量(variable)．
上面各个问题中，都出现了两个变量，它们互相依赖，密切相关．一般地，如果在一个变化过程中，有两个变量，例如x和y，对于x的每一个值，y都有惟一的值与之对应，我们就说x是自变量(independent variable)，y是因变量(dependent variable)，此时也称y是x的函数(fun_ction)． 表示函数关系的方法通常有三种： (1)解析法 如问题3中的， 这些表达式称为函数的关系式． (2)列表法 如问题2中的利率表，问题3中的波长与频率关系表． (3)图象法 如问题1中的气温曲线． 问题的研究过程中，还有一种量，它的取值始终保持不变，我们称之为常量(constant)，如问题3中的300 000 例: 写出下列各问题中的关系式，并指出其中的常量与变量：
(1)圆的周长C与半径r 的关系式；
(2)火车以60千米/时的速度行驶，它驶过的路程s（千米）和所用时间 t（时）的关系式；
(3) n 边形的内角和 S与边数n 的关系式．解: (1)C＝2π r，2π是常量，r、C是变量； (2)s＝60t，60是常量，t、s是变量；(3)S＝(n－2)×180，2、180是常量，n、S是变量．交流反思: 1.函数概念包含：(1)两个变量；(2)两个变量之间的对应关系．2.在某个变化过程中，可以取不同数值的量，叫做变量；数值始终保持不变的量，叫做常量．例如x和y，对于x的每一个值，y都有惟一的值与之对应，我们就说x是自变量，y是因变量．3.函数关系三种表示方法：(1)解析法；(2)列表法；(3)图象法 检测反馈 1.举3个日常生活中遇到的函数关系的例子．2.分别指出下列各关系式中的变量与常量：
(1)三角形的一边长5cm，它的面积S(cm2)与这边上的高h(cm)的关系式是；
(2)若直角三角形中的一个锐角的度数为α，则另一个锐角β(度)与α间的关系式是β＝90－α ；
(3)若某种报纸的单价为a元，x表示购买这种报纸的份数，则购买报纸的总价y（元）与x间的关系是：y＝ax．再 见制作:渠县双土中心学校 孙建