湖南省怀化市新晃县2022-2023学年九年级上学期期末考试数学试题(含答案)
文档属性
| 名称 | 湖南省怀化市新晃县2022-2023学年九年级上学期期末考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 355.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-14 22:04:05 | ||
图片预览


文档简介
新晃县2023年下期九年级期末质量检测
数 学
注意事项:
1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;
2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;
3.答题时,请考生注意各大题题号后面的答题提示;
4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;
5.答题卡上不得使用涂改液、涂改胶和贴纸;
6.本学科试卷共24个小题,考试时量120分钟,满分150分.
一、选择题(共24分)
1.的值为( )
A.1 B.2 C. D.
2.若点P(1,3)在反比例函数y=(k≠0)的图象上,则k的值是( )
A. B.3 C.- D.-3
3.将方程进行配方、配方正确的是( )
A. B. C. D.
4.已知正比例函数的图象与反比例函数的图象相交于点,下列说法正确的是( )
A.正比例函数的解析式是
B.两个函数图象的另一交点坐标为
C.正比例函数与反比例函数都随x的增大而增大
D.当或时,
5.某商品原价200元,连续两次降价a%后售价为148元,下列所列方程正确的是( )
A. B.
C. D.
6.有一个直角三角形的边长分别为3,4,5,另一个与它相似的直角三角形的最小边长为7,则另一个直角三角形的周长是( )
A. B. C.21 D.28
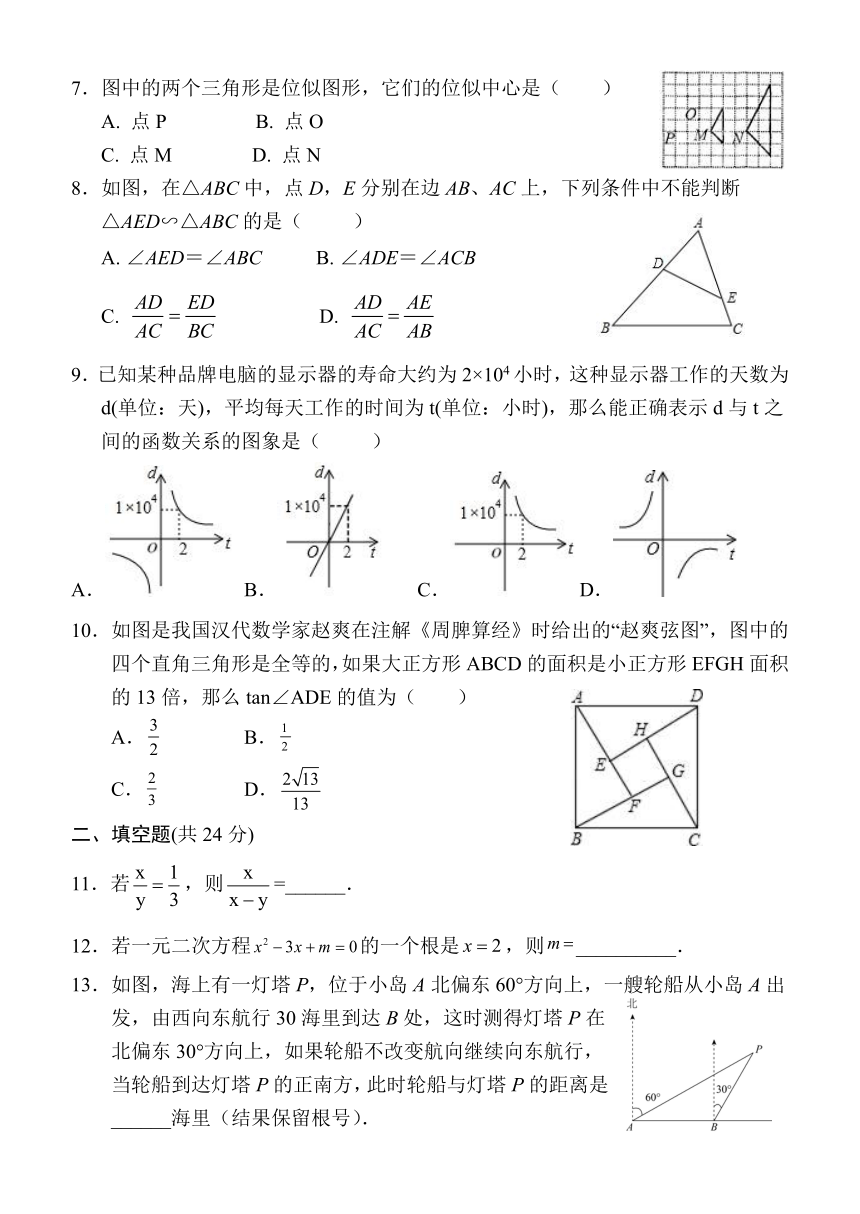
7.图中的两个三角形是位似图形,它们的位似中心是( )
A. 点P B. 点O
C. 点M D. 点N
8.如图,在△ABC中,点D,E分别在边AB、AC上,下列条件中不能判断△AED∽△ABC的是( )
A. ∠AED=∠ABC B. ∠ADE=∠ACB
C. D.
9.已知某种品牌电脑的显示器的寿命大约为2×104小时,这种显示器工作的天数为d(单位:天),平均每天工作的时间为t(单位:小时),那么能正确表示d与t之间的函数关系的图象是( )
A. B. C.D.
10.如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为( )
A. B.
C. D.
二、填空题(共24分)
11.若,则=______.
12.若一元二次方程的一个根是,则__________.
13.如图,海上有一灯塔P,位于小岛A北偏东60°方向上,一艘轮船从小岛A出发,由西向东航行30海里到达B处,这时测得灯塔P在北偏东30°方向上,如果轮船不改变航向继续向东航行,当轮船到达灯塔P的正南方,此时轮船与灯塔P的距离是______海里(结果保留根号).
14.某工厂一共有1200人,为选拔人才,提出了一些选拔的条件,并进行了抽样调查.从中抽出400人,发现有300人是符合条件的,那么则该工厂1200人中符合选拔条件的人数为________________.
15.如图,中,,,,,则的长是________.
16.如图,在平面直角坐标系中,菱形的面积为12,点在轴上,点在反比例函数()的图像上,则的值为______.
三、解答题(共86分)
17.(8分)用适当的方法解下列方程:
(1)
(2)
18.(8分)如图,DA⊥AB于A,EB⊥AB于B,C是AB上的动点,若∠DCE=90°.
求证:△ACD∽△BEC
19.(10分)已知反比例函数的图像经过点(2,-3).
(1)求这个函数的表达式.
(2)点(-1,6),(3,2)是否在这个函数的图像上?
(3)这个函数的图像位于哪些象限?函数值y随自变量的增大如何变化?
20.如图所示,游客在点A处坐缆车出发,沿A→B→D的路线可至山顶D处.假设AB和BD都是直线段,在B处看A处的俯角是15°,看D处的仰角是45°,且AB=BD=1000米,求山高DE的长.(参考数据:sin75°=0.97,cos75°≈0.26,≈1.41)
21.(12分)已知关于的一元二次方程有两个实数根.
(1)求的取值范围.
(2)若方程的两个实数根为和,,求的值.
22.(12分)某校为了解九年级全体学生物理实验操作的情况,随机抽取了30名学生的物理实验操作考核成绩,并将数据进行整理,分析如下(说明:考核成绩均取整数,A级:10分,B级:9分,C级:8分,D级:7分及以下) :
收集数据:10,8,10,9,5,10,9,9,10,8,9,10,9,9,8,9,8,10,7,9,8,10,9,6,9,10,9,10,8,10
整理数据,并绘制统计表如下:
成绩等级 A B C D
人数(名) 10 m n 3
根据表中的信息,解答下列问题:
(1)m=________,n=________.
(2)计算这30名学生的平均成绩.
(3)若该校九年级共有800名学生参加物理实验操作考核,成绩不低于9分为优秀,试估计该校九年级参加物理实验操作考核成绩达到优秀的学生有多少名?
23.(12分)如图,在中,,,垂足为,为上一点,连接,作交于.
(1)求证:.
(2)除(1)中相似三角形,图中还有其他相似三角形吗?如果有,请把它们都写出来.(证明不做要求)
24.(12分)如图,直线与双曲线 交于 A,B 两点,已知点 A 的坐标为( 3,1),点 B 的坐标为(, 3),直线 AB 与轴交于点 C,与轴交于点D.
(1)求双曲线和直线AB的解析式;
(2)若点P是双曲线上的一点,△OCP 的面积是△ODB 的面积的9倍,求点 P 的坐标;
(3)若点E在轴的负半轴上,是否存在以点 E,C,D 为顶点构成的三角形与△ODB相似?若存在,求出点E的坐标;若不存在,请说明理由.
九年级数学
一、选择题: CBDDB DACCC
二、填空题:11. ;12. 2;13. ;14.900;15. ;16.6
三、解答题:
17.(1) x1=,x2=2(4分 ); (2) x1=﹣3,x2=2(4分)
18.证明:∵AD⊥AB,BE⊥AB,∴∠DAC=90°=∠EBC,∴∠D+∠ACD=90°,
∵∠DCE=90°,∴∠DCA+∠ECB=90°,∴∠D=∠ECB,
∴△ACD∽△BEC.(8分)
19.(1) (4分);
(2)点(﹣1,6)在函数图象上,点(3,2)不在函数图象上(4分);
(3)∵k=﹣6<0,∴双曲线在二、四象限,在每个象限内y随x的增大而增大.(4分)
20.解:由题意得:∠ACB=∠BFD=90°,EF=BC,且∠ABC=75°,∠DBF=45°(2分)
在Rt△ABC中,∠ACB=90°,∠ABC=75°,
∵cos75°=,∴BC=AB cos75°≈1000×0.26=260(米).
∴EF=BC=260.(7分)
在Rt△BDF中,∠BFD=90°,∠DBF=45°,
∵sin45°=,∴DF=BD sin45°=1000×≈500×1.41=705(米).
∴DE=DF+EF=705+260=965(米).
∴山高DE约为965米.(12分)
21.(1)且(6分);(2)(6分)
22.(1)11,5(4分);(2)8.8分(4分);(3)560名(4分)
23.(1)∵ ∴ ,
∴
又∵ ,∴ ,
又∵ ∴ ,
又∵ ,∴ ,
∴ ,
∴ (6分)
(2)∵ ,∴ ;
∴ ,∴ ,
同理得 ,
∴ ,
即 .(6分)
24.(1)由A(-3,1)得 (1分)
从而,所以B点为(1,-3).(2分)
由此得 解之得
所以双曲线的解析式为,直线的解析式为(4分)
(2)如图1,C、D是直线与坐标轴的交点,所以C为(-2,0)、D为(0,-2)
则OD=OC=2,
由于P在双曲线上,可设P点的坐标为,则
据题意有,从而得
所求P点的坐标为(或(4分)
(3)存在,E点坐标为(-6,0)或(-4,0)(1 分)
如图2,不难计算DB=,是等腰直角三角形,且CD=,从而
因此,若E存在,显然E只能在C的左边,
设E的坐标为(,0),
要与相似,则要或
即或
解之得或
所以E点坐标为(-6,0)或(-4,0)。(4分)
数 学
注意事项:
1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;
2.必须在答题卡上答题,在草稿纸、试题卷上答题无效;
3.答题时,请考生注意各大题题号后面的答题提示;
4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁;
5.答题卡上不得使用涂改液、涂改胶和贴纸;
6.本学科试卷共24个小题,考试时量120分钟,满分150分.
一、选择题(共24分)
1.的值为( )
A.1 B.2 C. D.
2.若点P(1,3)在反比例函数y=(k≠0)的图象上,则k的值是( )
A. B.3 C.- D.-3
3.将方程进行配方、配方正确的是( )
A. B. C. D.
4.已知正比例函数的图象与反比例函数的图象相交于点,下列说法正确的是( )
A.正比例函数的解析式是
B.两个函数图象的另一交点坐标为
C.正比例函数与反比例函数都随x的增大而增大
D.当或时,
5.某商品原价200元,连续两次降价a%后售价为148元,下列所列方程正确的是( )
A. B.
C. D.
6.有一个直角三角形的边长分别为3,4,5,另一个与它相似的直角三角形的最小边长为7,则另一个直角三角形的周长是( )
A. B. C.21 D.28
7.图中的两个三角形是位似图形,它们的位似中心是( )
A. 点P B. 点O
C. 点M D. 点N
8.如图,在△ABC中,点D,E分别在边AB、AC上,下列条件中不能判断△AED∽△ABC的是( )
A. ∠AED=∠ABC B. ∠ADE=∠ACB
C. D.
9.已知某种品牌电脑的显示器的寿命大约为2×104小时,这种显示器工作的天数为d(单位:天),平均每天工作的时间为t(单位:小时),那么能正确表示d与t之间的函数关系的图象是( )
A. B. C.D.
10.如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为( )
A. B.
C. D.
二、填空题(共24分)
11.若,则=______.
12.若一元二次方程的一个根是,则__________.
13.如图,海上有一灯塔P,位于小岛A北偏东60°方向上,一艘轮船从小岛A出发,由西向东航行30海里到达B处,这时测得灯塔P在北偏东30°方向上,如果轮船不改变航向继续向东航行,当轮船到达灯塔P的正南方,此时轮船与灯塔P的距离是______海里(结果保留根号).
14.某工厂一共有1200人,为选拔人才,提出了一些选拔的条件,并进行了抽样调查.从中抽出400人,发现有300人是符合条件的,那么则该工厂1200人中符合选拔条件的人数为________________.
15.如图,中,,,,,则的长是________.
16.如图,在平面直角坐标系中,菱形的面积为12,点在轴上,点在反比例函数()的图像上,则的值为______.
三、解答题(共86分)
17.(8分)用适当的方法解下列方程:
(1)
(2)
18.(8分)如图,DA⊥AB于A,EB⊥AB于B,C是AB上的动点,若∠DCE=90°.
求证:△ACD∽△BEC
19.(10分)已知反比例函数的图像经过点(2,-3).
(1)求这个函数的表达式.
(2)点(-1,6),(3,2)是否在这个函数的图像上?
(3)这个函数的图像位于哪些象限?函数值y随自变量的增大如何变化?
20.如图所示,游客在点A处坐缆车出发,沿A→B→D的路线可至山顶D处.假设AB和BD都是直线段,在B处看A处的俯角是15°,看D处的仰角是45°,且AB=BD=1000米,求山高DE的长.(参考数据:sin75°=0.97,cos75°≈0.26,≈1.41)
21.(12分)已知关于的一元二次方程有两个实数根.
(1)求的取值范围.
(2)若方程的两个实数根为和,,求的值.
22.(12分)某校为了解九年级全体学生物理实验操作的情况,随机抽取了30名学生的物理实验操作考核成绩,并将数据进行整理,分析如下(说明:考核成绩均取整数,A级:10分,B级:9分,C级:8分,D级:7分及以下) :
收集数据:10,8,10,9,5,10,9,9,10,8,9,10,9,9,8,9,8,10,7,9,8,10,9,6,9,10,9,10,8,10
整理数据,并绘制统计表如下:
成绩等级 A B C D
人数(名) 10 m n 3
根据表中的信息,解答下列问题:
(1)m=________,n=________.
(2)计算这30名学生的平均成绩.
(3)若该校九年级共有800名学生参加物理实验操作考核,成绩不低于9分为优秀,试估计该校九年级参加物理实验操作考核成绩达到优秀的学生有多少名?
23.(12分)如图,在中,,,垂足为,为上一点,连接,作交于.
(1)求证:.
(2)除(1)中相似三角形,图中还有其他相似三角形吗?如果有,请把它们都写出来.(证明不做要求)
24.(12分)如图,直线与双曲线 交于 A,B 两点,已知点 A 的坐标为( 3,1),点 B 的坐标为(, 3),直线 AB 与轴交于点 C,与轴交于点D.
(1)求双曲线和直线AB的解析式;
(2)若点P是双曲线上的一点,△OCP 的面积是△ODB 的面积的9倍,求点 P 的坐标;
(3)若点E在轴的负半轴上,是否存在以点 E,C,D 为顶点构成的三角形与△ODB相似?若存在,求出点E的坐标;若不存在,请说明理由.
九年级数学
一、选择题: CBDDB DACCC
二、填空题:11. ;12. 2;13. ;14.900;15. ;16.6
三、解答题:
17.(1) x1=,x2=2(4分 ); (2) x1=﹣3,x2=2(4分)
18.证明:∵AD⊥AB,BE⊥AB,∴∠DAC=90°=∠EBC,∴∠D+∠ACD=90°,
∵∠DCE=90°,∴∠DCA+∠ECB=90°,∴∠D=∠ECB,
∴△ACD∽△BEC.(8分)
19.(1) (4分);
(2)点(﹣1,6)在函数图象上,点(3,2)不在函数图象上(4分);
(3)∵k=﹣6<0,∴双曲线在二、四象限,在每个象限内y随x的增大而增大.(4分)
20.解:由题意得:∠ACB=∠BFD=90°,EF=BC,且∠ABC=75°,∠DBF=45°(2分)
在Rt△ABC中,∠ACB=90°,∠ABC=75°,
∵cos75°=,∴BC=AB cos75°≈1000×0.26=260(米).
∴EF=BC=260.(7分)
在Rt△BDF中,∠BFD=90°,∠DBF=45°,
∵sin45°=,∴DF=BD sin45°=1000×≈500×1.41=705(米).
∴DE=DF+EF=705+260=965(米).
∴山高DE约为965米.(12分)
21.(1)且(6分);(2)(6分)
22.(1)11,5(4分);(2)8.8分(4分);(3)560名(4分)
23.(1)∵ ∴ ,
∴
又∵ ,∴ ,
又∵ ∴ ,
又∵ ,∴ ,
∴ ,
∴ (6分)
(2)∵ ,∴ ;
∴ ,∴ ,
同理得 ,
∴ ,
即 .(6分)
24.(1)由A(-3,1)得 (1分)
从而,所以B点为(1,-3).(2分)
由此得 解之得
所以双曲线的解析式为,直线的解析式为(4分)
(2)如图1,C、D是直线与坐标轴的交点,所以C为(-2,0)、D为(0,-2)
则OD=OC=2,
由于P在双曲线上,可设P点的坐标为,则
据题意有,从而得
所求P点的坐标为(或(4分)
(3)存在,E点坐标为(-6,0)或(-4,0)(1 分)
如图2,不难计算DB=,是等腰直角三角形,且CD=,从而
因此,若E存在,显然E只能在C的左边,
设E的坐标为(,0),
要与相似,则要或
即或
解之得或
所以E点坐标为(-6,0)或(-4,0)。(4分)
同课章节目录
