18.1 变量与函数1[下学期]
图片预览





文档简介
课件26张PPT。 这种一个量随另一个量的变化而变化的现象大量存在。行星在宇宙中的位置随时间而变化;
人体细胞的个数随年龄而变化;
气温随海拔而变化;
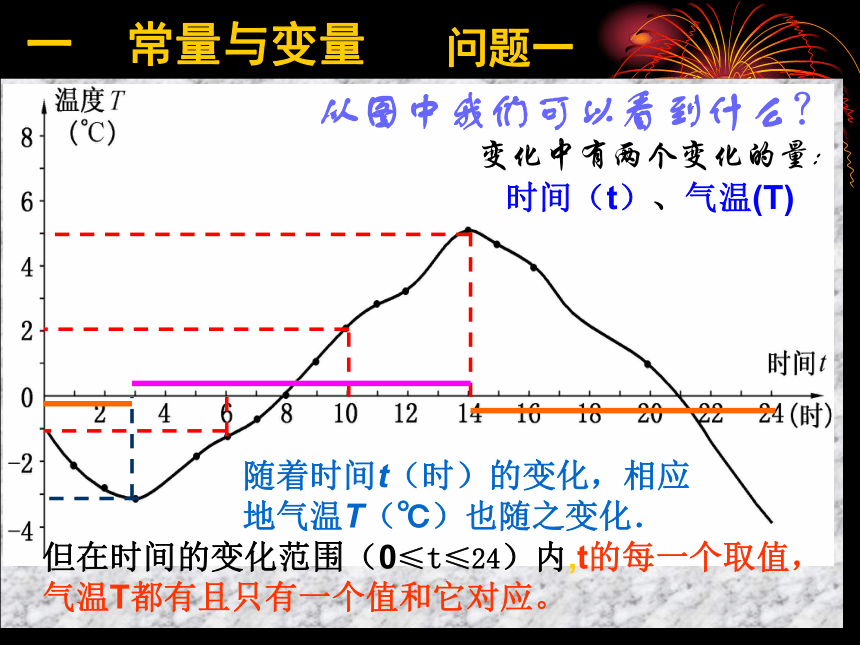
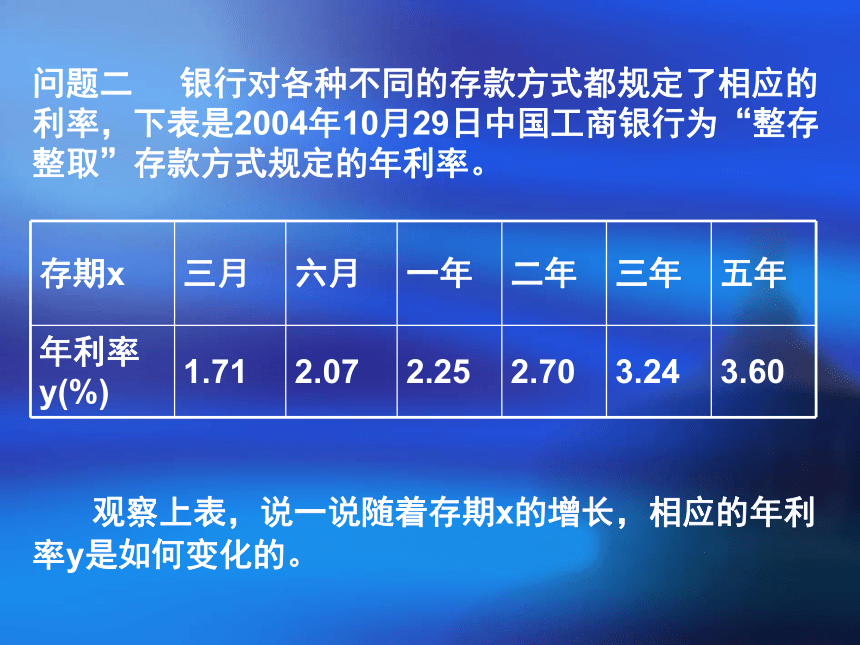
汽车行驶里程随行驶时间而变化…… 大千世界处在不停的运动变化之中,如何来研究这些运动变化并寻找规律呢? 数学上常用变量与函数来刻画各种运动变化。 这一章我们将通过实际问题着重研究有关函数及其图像的初步知识。17.1变量与函数天星中学问题一一 常量与变量从图中我们可以看到什么?随着时间t(时)的变化,相应地气温T(℃)也随之变化.变化中有两个变化的量:时间(t)、气温(T)但在时间的变化范围(0≤t≤24)内,t的每一个取值,气温T都有且只有一个值和它对应。问题二 银行对各种不同的存款方式都规定了相应的利率,下表是2004年10月29日中国工商银行为“整存整取”存款方式规定的年利率。 观察上表,说一说随着存期x的增长,相应的年利率y是如何变化的。问题三 收音机上的刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值:l与f之间有什么关系吗?这说明波长l越大,
频率f就______ 。l与f的乘积是个定值。还可以看到:给出波长l的一个数值,
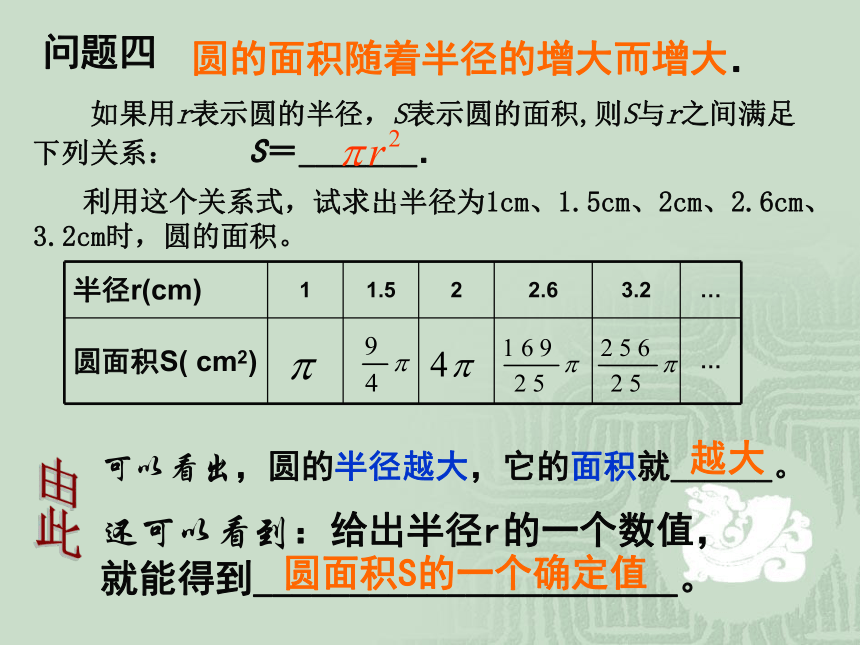
就能得到________________。越小频率f的一个确定值问题四 如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系: S=_______.圆的面积随着半径的增大而增大. 利用这个关系式,试求出半径为1cm、1.5cm、2cm、2.6cm、3.2cm时,圆的面积。越大还可以看到:给出半径r的一个数值,
就能得到______________________。圆面积S的一个确定值爱无国界 情系灾区每人捐赠数×人数=总钱数每人捐赠数 →不变
人数 → 变化
总钱数 → 变化变量常量 在上面的问题中研究了一些数量关系,它们都刻画了某些变化规律. 变化中出现了各种各样的量,其中有一些是数值会发生变化的量. 例如问题1中,刻画气温变化规律的量是时间t和气温T,气温T 随着时间t的变化而变化,它们都会取不同的数值.同时还有一种量,它的取值始终保持不变。如问题3中的300 000,问题4中的π等.常量变量 在某一变化过程中,可以取不同数值的量,叫做变量. 在研究问题的过程中,取值始终保持不变的量,叫做常量.常量与变量如图,△ABC中,底边BC边上的高为6,当顶点C沿底边所在的直线向B点运动时,三角形的面积(S)与底边BC(x)的关系式.试一试底边BC长(X) ×高AD=面积(S)变量 常量变量想一想在时间t,速度v,路程s的关系式s=vt中(1)若v保持不变,判断此问题中的常量和变量;(2)若s保持不变,判断此问题中的常量和变量;(3)若t保持不变,判断此问题中的常量和变量;常量与变量的区分并非绝对的,一个问题中的常量在另一个问题中可能是变量。例1 指出下列关系式中的常量和变量:
(1)球的体积V与球的半径r的关系式:
(2)解: (1) 是常量,r,V是变量;(2) 是常量,S,h是变量。判断常量与变量时,
(1)应抓住变与不变;
(2)要注意并不是关系式中的所有字母都表示变量;
(3)圆周率 是一个常数,是不变的。练习:指出关系式中的常量与变量:
(1)
(2)
(3)二 函数函数的定义函数是刻画和研究现实世界数量关系的重要数学模型如果在一个变化过程中,有两个变量x与y,对于x的每一个确定的值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量,y是x的函数.关于函数定义的理解:(1)它有两个变量;例如:圆的面积公式 中,r是自变量,S是因变量。如果出现一个变量或多个变量时,就不是函数关系。又如: 只是代数式而不是函数关系;
三角形面积公式 ,如果S,a,h都不确定,就不能说S是a,h的函数。(2)“对于x的每一个值”指的是x在其允许的取值范围内取的每一个确定值,这个允许取值范围就是函数自变量的取值范围;例如:函数 中,要使函数有意义,x必须为大于等于3的实数,对于在 范围内的每一个x的值,y都有唯一确定的值与之对应。(3)“y有唯一值与之对应”是指在自变量的取值范围内,x每取一个确定的值,y都有唯一的值与之对应,否则y不是x的函数;例如:函数 中,尽管x与y之间有关系式,但是由于x在x>0的范围内每取一个值,y都有两个确定的值与它对应,所以y不是x的函数。判断两个变量是否有函数关系,要同时满足(1)有两个变量(2)自变量 x每取一个确定的值,因变量y都有唯一的值与之对应。(4)x取不同的值,y的取值可以相同;例如:函数 中,x=2时,y=1;x=4时,y=1。 判断两个变量是否有函数关系,关键是看自变量在其取值范围内每取一个确定的值时,因变量是否总有唯一确定的值与之对应,“唯一”和“对应”是函数的本质属性,至于自变量变化时,因变量是否变化,无关紧要。
例如函数:(5)函数不是数,它是指在一个变化过程中两个变量之间的对应关系。 函数的本质 就是变量间的对应关系 “对应”关系有些可以用数学式子表达,有些不能用数学式子表达。例如问题一。小结:一 常量与变量 在某一变化过程中,可以取不同数值的量,叫做变量. 在研究问题的过程中,取值始终保持不变的量,叫做常量.二 函数函数的定义: 如果在一个变化过程中,有两个变量x与y,对于x的每一个确定的值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量,y是x的函数. 例2 指出下列函数中的自变量,因变量,函数和常量。
(1)
(2)例4 判断下列两个变量是否有函数关系,若有,关系式是什么?
(1)正方形的面积和周长;(2)矩形的面积与周长。解: (1)因为对于正方形周长的每一个确定的值,都有唯一确定的正方形的边长,因此都有唯一确定的正方形的面积值与之对应,所以正方形面积是其周长的函数。 (2)因为对于矩形周长的每一个确定的值,它的长和宽不是唯一确定的,这样矩形周长对应的矩形面积并不是唯一确定的,所以,矩形的面积不是它的周长的函数。例5 下列关系中,y不是x的函数的有:
人体细胞的个数随年龄而变化;
气温随海拔而变化;
汽车行驶里程随行驶时间而变化…… 大千世界处在不停的运动变化之中,如何来研究这些运动变化并寻找规律呢? 数学上常用变量与函数来刻画各种运动变化。 这一章我们将通过实际问题着重研究有关函数及其图像的初步知识。17.1变量与函数天星中学问题一一 常量与变量从图中我们可以看到什么?随着时间t(时)的变化,相应地气温T(℃)也随之变化.变化中有两个变化的量:时间(t)、气温(T)但在时间的变化范围(0≤t≤24)内,t的每一个取值,气温T都有且只有一个值和它对应。问题二 银行对各种不同的存款方式都规定了相应的利率,下表是2004年10月29日中国工商银行为“整存整取”存款方式规定的年利率。 观察上表,说一说随着存期x的增长,相应的年利率y是如何变化的。问题三 收音机上的刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值:l与f之间有什么关系吗?这说明波长l越大,
频率f就______ 。l与f的乘积是个定值。还可以看到:给出波长l的一个数值,
就能得到________________。越小频率f的一个确定值问题四 如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系: S=_______.圆的面积随着半径的增大而增大. 利用这个关系式,试求出半径为1cm、1.5cm、2cm、2.6cm、3.2cm时,圆的面积。越大还可以看到:给出半径r的一个数值,
就能得到______________________。圆面积S的一个确定值爱无国界 情系灾区每人捐赠数×人数=总钱数每人捐赠数 →不变
人数 → 变化
总钱数 → 变化变量常量 在上面的问题中研究了一些数量关系,它们都刻画了某些变化规律. 变化中出现了各种各样的量,其中有一些是数值会发生变化的量. 例如问题1中,刻画气温变化规律的量是时间t和气温T,气温T 随着时间t的变化而变化,它们都会取不同的数值.同时还有一种量,它的取值始终保持不变。如问题3中的300 000,问题4中的π等.常量变量 在某一变化过程中,可以取不同数值的量,叫做变量. 在研究问题的过程中,取值始终保持不变的量,叫做常量.常量与变量如图,△ABC中,底边BC边上的高为6,当顶点C沿底边所在的直线向B点运动时,三角形的面积(S)与底边BC(x)的关系式.试一试底边BC长(X) ×高AD=面积(S)变量 常量变量想一想在时间t,速度v,路程s的关系式s=vt中(1)若v保持不变,判断此问题中的常量和变量;(2)若s保持不变,判断此问题中的常量和变量;(3)若t保持不变,判断此问题中的常量和变量;常量与变量的区分并非绝对的,一个问题中的常量在另一个问题中可能是变量。例1 指出下列关系式中的常量和变量:
(1)球的体积V与球的半径r的关系式:
(2)解: (1) 是常量,r,V是变量;(2) 是常量,S,h是变量。判断常量与变量时,
(1)应抓住变与不变;
(2)要注意并不是关系式中的所有字母都表示变量;
(3)圆周率 是一个常数,是不变的。练习:指出关系式中的常量与变量:
(1)
(2)
(3)二 函数函数的定义函数是刻画和研究现实世界数量关系的重要数学模型如果在一个变化过程中,有两个变量x与y,对于x的每一个确定的值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量,y是x的函数.关于函数定义的理解:(1)它有两个变量;例如:圆的面积公式 中,r是自变量,S是因变量。如果出现一个变量或多个变量时,就不是函数关系。又如: 只是代数式而不是函数关系;
三角形面积公式 ,如果S,a,h都不确定,就不能说S是a,h的函数。(2)“对于x的每一个值”指的是x在其允许的取值范围内取的每一个确定值,这个允许取值范围就是函数自变量的取值范围;例如:函数 中,要使函数有意义,x必须为大于等于3的实数,对于在 范围内的每一个x的值,y都有唯一确定的值与之对应。(3)“y有唯一值与之对应”是指在自变量的取值范围内,x每取一个确定的值,y都有唯一的值与之对应,否则y不是x的函数;例如:函数 中,尽管x与y之间有关系式,但是由于x在x>0的范围内每取一个值,y都有两个确定的值与它对应,所以y不是x的函数。判断两个变量是否有函数关系,要同时满足(1)有两个变量(2)自变量 x每取一个确定的值,因变量y都有唯一的值与之对应。(4)x取不同的值,y的取值可以相同;例如:函数 中,x=2时,y=1;x=4时,y=1。 判断两个变量是否有函数关系,关键是看自变量在其取值范围内每取一个确定的值时,因变量是否总有唯一确定的值与之对应,“唯一”和“对应”是函数的本质属性,至于自变量变化时,因变量是否变化,无关紧要。
例如函数:(5)函数不是数,它是指在一个变化过程中两个变量之间的对应关系。 函数的本质 就是变量间的对应关系 “对应”关系有些可以用数学式子表达,有些不能用数学式子表达。例如问题一。小结:一 常量与变量 在某一变化过程中,可以取不同数值的量,叫做变量. 在研究问题的过程中,取值始终保持不变的量,叫做常量.二 函数函数的定义: 如果在一个变化过程中,有两个变量x与y,对于x的每一个确定的值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量,y是x的函数. 例2 指出下列函数中的自变量,因变量,函数和常量。
(1)
(2)例4 判断下列两个变量是否有函数关系,若有,关系式是什么?
(1)正方形的面积和周长;(2)矩形的面积与周长。解: (1)因为对于正方形周长的每一个确定的值,都有唯一确定的正方形的边长,因此都有唯一确定的正方形的面积值与之对应,所以正方形面积是其周长的函数。 (2)因为对于矩形周长的每一个确定的值,它的长和宽不是唯一确定的,这样矩形周长对应的矩形面积并不是唯一确定的,所以,矩形的面积不是它的周长的函数。例5 下列关系中,y不是x的函数的有:
