18.1 变量与函数[下学期]
图片预览







文档简介
课件20张PPT。变量与函数 大千世界处在不停的运动变化之中,如何 来研究这些运动变化并寻找规律呢?
数学上常用变量与函数来刻画各种运动变化. 在日常学习和生活中,我们常要研究一些数量关系:
小明到商店买练习簿,每本单价2元,
购买的总数x(本)与总金额y(元)的关系式,
可以表示为
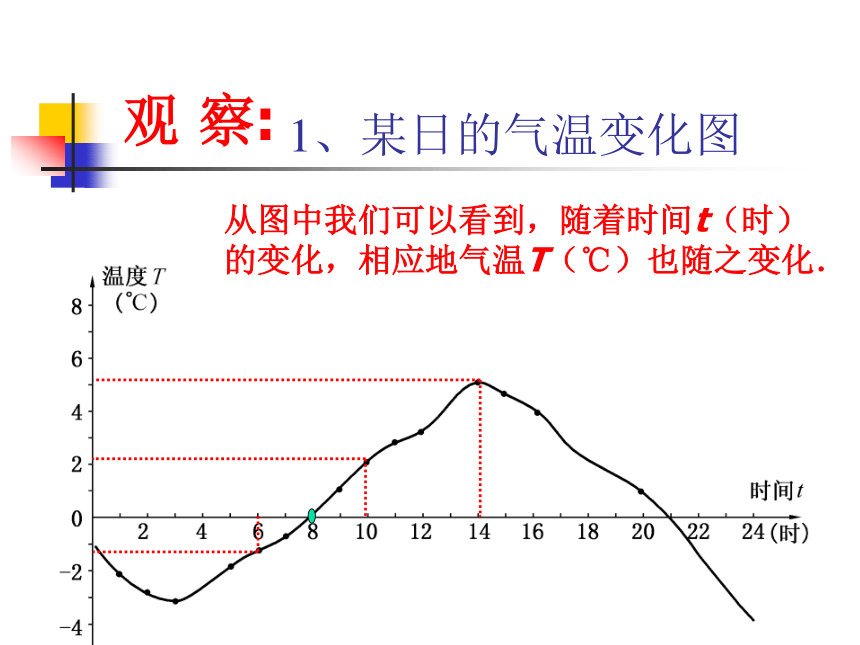
创设情境:其中y随x的变化而变化1、某日的气温变化图
从图中我们可以看到,随着时间t(时)
的变化,相应地气温T(℃)也随之变化. 观 察:2、 2002年7月中国工商银行为
“整存整取”的存款方式规定的利率
观察上表,说说随着存期x的增长,
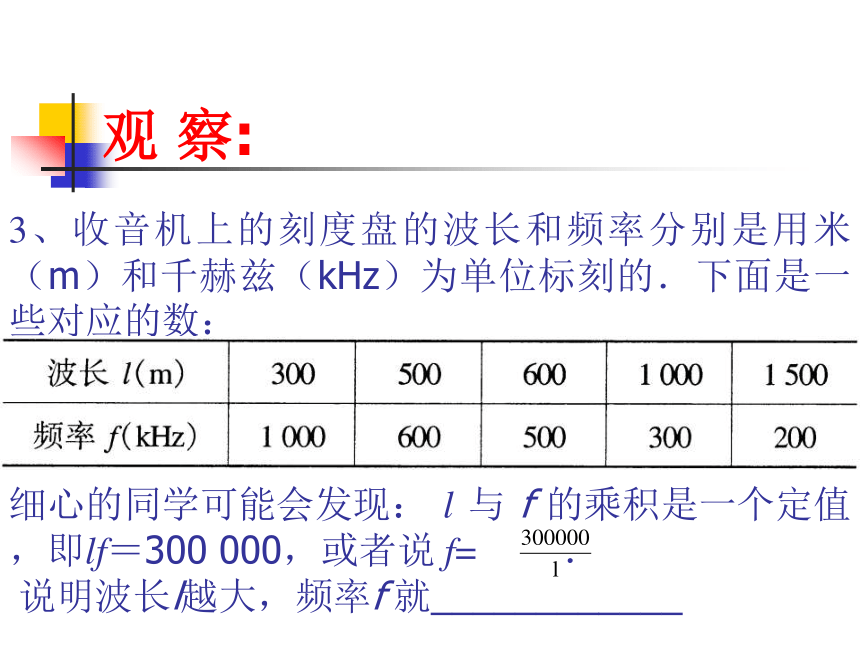
相应的利率y是如何变化的.观 察:3、收音机上的刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数:
细心的同学可能会发现: l 与 f 的乘积是一个定值,即lf=300 000,或者说 f= .
?说明波长l越大,频率f 就____________ 观 察:观 察:
圆面积S与半径r的关系 圆的面积随着半径的增大而增大.如果用r表示圆的半径,S表示圆的面积。
则S与r之间满足下列关系:S=____________. 在某一变化过程中,可以取不同数值的量,
叫做变量(variable).
在问题的研究过程中,还有一种量,它的取值始终保持不变,我们称之为常量(constant),概 括 一般地,在一个变化过程中有两个变量x与y,如果对于x每 一个值,y都有唯一的值与它对应,那么就说x是
自变量,y是因变量,此时也称 y是x的函数。 日常生活和自然界中函数的事例很多: 如: 当矩形的长一定时,矩形的面积依赖宽的变化而变化
他们之间是否存在函数关系呢?概 括 试一试:看谁的眼光准例1、判断下列变量关系是不是函数?(1)等腰三角形的底边长与面积判断是不是函数,我们可以看它的数学式子中的变量之间是否满足函数的定义表示函数关系的方法通常有三种:
?
(1) 解析法,如观察3中的f= ,观察4中的
S=πr2,这些表达式称为函数的关系式.
?
(2) 列表法,如观察2中的利率表,观察3中
的波长与频率关系表.
?
(3) 图象法,观察1中的气温曲线. 表示函数关系的方法函数的关系式是等式
那么函数解析式的书写有没有要求呢?通常等式的右边是含有自变量的代数式,
左边的一个字母表示函数如何去书写呢??(1)圆的周长C与半径r的关系式;
(2)火车以60千米/时的速度行驶,它 驶过的路程
s(千米)和所用时间t(时)的关系式;
(3)n边形的内角和S与边数n的关系式. 写出下列各问题中的关系式,并指出其中的常量与变量教你一招:1、先认真审题,根据题意找出相等关系2、按相等关系,写出含有两个变量的等式3、将等式变形为用含有自变量的代数式
表示函数的式子 1、y 比 x的 少22、y 是 x的 倒数的4倍
根据所给的 条件,写出y与x的函数关系式: 3、矩形的周长是18 cm ,它的长是y,
宽是x cm ;汽车由洪泽驶往相距500公里外的上海,它的平均速度是100 公里/小时,则汽车距上海的的距离s(公里)与行驶时间t(小时)的函数关系式?你 能仿照此题编一道题目吗?认真审题:你会有意外的收获课堂检测:1、在y=3x+1中,如果x 是自变量, 是x的函数2、下列说法中,不正确的是( )A、函数不是数,而是 一种关系
B、多边形的内角和是边数的函数
C、一天中时间是温度的函数
D、一天中温度是时间的函数3、正方形的边长为5 cm,当边长减少x cm时,周长为y cm,求y与x的函数关系式。拓展迁移:某汽车的油箱内装有30 公升的油,行驶时每百公里耗油2.5公升,设行使的里程为X(百公里),求油箱中所剩下的油 y (公升)与x之间的函数关系式?当x=10时,y=?
当x=12.1时,y=?
当x=12时,y=?
课堂小结:
本节课我们学习主要内容是什么?
你有什么收获?下 课
Goodbye!
数学上常用变量与函数来刻画各种运动变化. 在日常学习和生活中,我们常要研究一些数量关系:
小明到商店买练习簿,每本单价2元,
购买的总数x(本)与总金额y(元)的关系式,
可以表示为
创设情境:其中y随x的变化而变化1、某日的气温变化图
从图中我们可以看到,随着时间t(时)
的变化,相应地气温T(℃)也随之变化. 观 察:2、 2002年7月中国工商银行为
“整存整取”的存款方式规定的利率
观察上表,说说随着存期x的增长,
相应的利率y是如何变化的.观 察:3、收音机上的刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数:
细心的同学可能会发现: l 与 f 的乘积是一个定值,即lf=300 000,或者说 f= .
?说明波长l越大,频率f 就____________ 观 察:观 察:
圆面积S与半径r的关系 圆的面积随着半径的增大而增大.如果用r表示圆的半径,S表示圆的面积。
则S与r之间满足下列关系:S=____________. 在某一变化过程中,可以取不同数值的量,
叫做变量(variable).
在问题的研究过程中,还有一种量,它的取值始终保持不变,我们称之为常量(constant),概 括 一般地,在一个变化过程中有两个变量x与y,如果对于x每 一个值,y都有唯一的值与它对应,那么就说x是
自变量,y是因变量,此时也称 y是x的函数。 日常生活和自然界中函数的事例很多: 如: 当矩形的长一定时,矩形的面积依赖宽的变化而变化
他们之间是否存在函数关系呢?概 括 试一试:看谁的眼光准例1、判断下列变量关系是不是函数?(1)等腰三角形的底边长与面积判断是不是函数,我们可以看它的数学式子中的变量之间是否满足函数的定义表示函数关系的方法通常有三种:
?
(1) 解析法,如观察3中的f= ,观察4中的
S=πr2,这些表达式称为函数的关系式.
?
(2) 列表法,如观察2中的利率表,观察3中
的波长与频率关系表.
?
(3) 图象法,观察1中的气温曲线. 表示函数关系的方法函数的关系式是等式
那么函数解析式的书写有没有要求呢?通常等式的右边是含有自变量的代数式,
左边的一个字母表示函数如何去书写呢??(1)圆的周长C与半径r的关系式;
(2)火车以60千米/时的速度行驶,它 驶过的路程
s(千米)和所用时间t(时)的关系式;
(3)n边形的内角和S与边数n的关系式. 写出下列各问题中的关系式,并指出其中的常量与变量教你一招:1、先认真审题,根据题意找出相等关系2、按相等关系,写出含有两个变量的等式3、将等式变形为用含有自变量的代数式
表示函数的式子 1、y 比 x的 少22、y 是 x的 倒数的4倍
根据所给的 条件,写出y与x的函数关系式: 3、矩形的周长是18 cm ,它的长是y,
宽是x cm ;汽车由洪泽驶往相距500公里外的上海,它的平均速度是100 公里/小时,则汽车距上海的的距离s(公里)与行驶时间t(小时)的函数关系式?你 能仿照此题编一道题目吗?认真审题:你会有意外的收获课堂检测:1、在y=3x+1中,如果x 是自变量, 是x的函数2、下列说法中,不正确的是( )A、函数不是数,而是 一种关系
B、多边形的内角和是边数的函数
C、一天中时间是温度的函数
D、一天中温度是时间的函数3、正方形的边长为5 cm,当边长减少x cm时,周长为y cm,求y与x的函数关系式。拓展迁移:某汽车的油箱内装有30 公升的油,行驶时每百公里耗油2.5公升,设行使的里程为X(百公里),求油箱中所剩下的油 y (公升)与x之间的函数关系式?当x=10时,y=?
当x=12.1时,y=?
当x=12时,y=?
课堂小结:
本节课我们学习主要内容是什么?
你有什么收获?下 课
Goodbye!
