19.2.2菱形的判定 课件(共25张PPT)
文档属性
| 名称 | 19.2.2菱形的判定 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-15 07:01:09 | ||
图片预览






文档简介
(共25张PPT)
19.2.2菱形的判定
华师大版 八年级 下册
教学目标
教学目标:1.经历菱形判定定理的探究过程,掌握菱形的判定定理.
2.会用这些菱形的判定方法进行有关的证明和计算.
教学重点:菱形判定定理的掌握和应用.
教学难点:菱形判定定理的灵活应用.
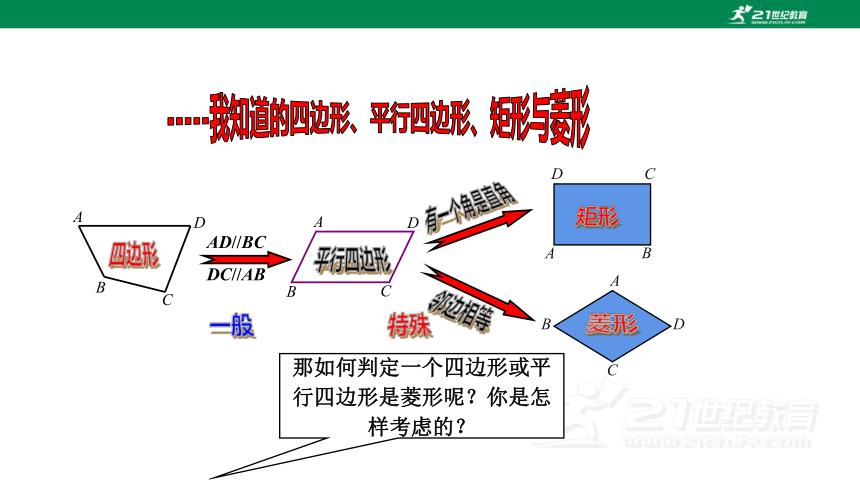
-----我知道的四边形、平行四边形、矩形与菱形
平行四边形
A
B
C
D
四边形
A
B
C
D
AD//BC
DC//AB
一般
特殊
有一个角是直角
A
B
C
D
矩形
邻边相等
D
A
B
C
菱形
那如何判定一个四边形或平行四边形是菱形呢?你是怎样考虑的?
新知导入
情境引入
1.定义:一组邻边相等的平行四边形叫做菱形.
菱形的定义作为我们判定菱形的基本方法,接下来我们从边上来研究菱形的判定方法.
∵四边形ABCD是平行四边形,AB=AD.
∴四边形ABCD是菱形.
数学语言
四条边相等的四边形是菱形.
菱形的四条边相等.
逆命题
这个逆命题成立吗?
新知讲解
合作学习
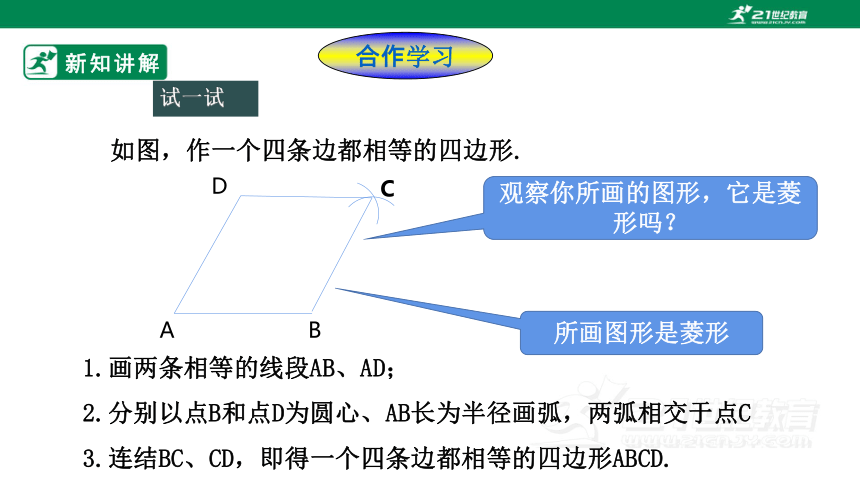
试一试
如图,作一个四条边都相等的四边形.
1.画两条相等的线段AB、AD;
2.分别以点B和点D为圆心、AB长为半径画弧,两弧相交于点C
3.连结BC、CD,即得一个四条边都相等的四边形ABCD.
A
B
D
C
观察你所画的图形,它是菱形吗?
所画图形是菱形
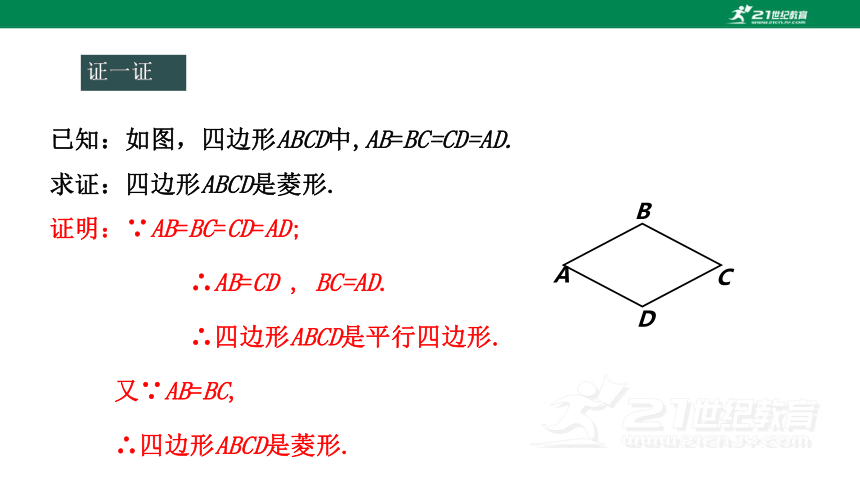
证一证
证明:∵AB=BC=CD=AD;
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
A
B
C
D
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
四条边都相等的四边形是菱形
AB=BC=CD=AD
几何语言:
∵在四边形ABCD中,AB=BC=CD=AD,
∴四边形 ABCD是菱形.
A
B
C
D
菱形ABCD
四边形ABCD
A
B
C
D
菱形的判定定理1:
思考
菱形的两条对角线互相垂直
这是菱形所特有的性质.你能从对角线的角度得到什么关于菱形判定的猜想?
猜想:对角线互相垂直的平行四边形是菱形.
试一试
前面我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形 对此你有什么猜想?
做一做
作一条两条对角线互相垂直的平行四边形.
步骤:
1.作两条互相垂直的直线m、n,记交点为点O;
2.以点 O为圆心、适当长为半径画弧,
在直线 m,n上分别截取相等的
两组线段OA、OC和OB、OD ;
3.连接A、B、C、D四点 ,显然,
它是一个对角线互相垂直的平行四边形.
m
n
O
A
B
C
D
提炼概念
对角线互相垂直的平行四边形是菱形.
AC⊥BD
几何语言:
∵在□ABCD中,AC⊥BD,
∴ □ABCD是菱形.
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
菱形的判定定理2:
典例精讲
例4 如图,在矩形ABCD中,点E、F、G、H分别是四条边的中点,试问四边形EFGH是什么图形?并说明理由.
解:∵H点为AD的中点,∴AH=HD,
∵E点为AB的中点,AE= AB,
G点为DC的中点,DG= CD ,
又∵AB=DC,∴AE=DG.
∵∠HAE=∠HDG,∴△EAH≌△GDH , ∴HE=HG ,
同理EF=FG=HG=HE ,
∴四边形EFGH是菱形.
例5 如图,已知矩形ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F.
求证:四边形AFCE是菱形.
分析:要证四边形AFCE是菱形,由已知条件可知EF⊥AC,所以只需证明四边形AFCE是平行四边形,又知EF垂直平分AC,所以只需证明OE=OF.
证明:∵四边形ABCD是矩形,∴AE∥FC,
∴∠1=∠2.
∵EF平分AC,∴OA=OC.
又∵∠AOE=∠COF=90°,
∴△AOE≌△COF, ∴OE=OF,
∴四边形AFCE是平行四边形.
又∵EF⊥AC,
∴四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).
归纳概念
定义:有一组邻边相等的平行四边形叫做菱形
判定定理1:四边都相等的四边形是菱形
菱形的判定
对角线互相垂直的平行四边形是菱形.
课堂练习
1、判断题
(1)对角线互相垂直的四边形是菱形( )
(2)一条对角线垂直另一条对角线的四边形是菱形( )
(3)对角线互相垂直且平分的四边形是菱形( )
(4)对角线相等的四边形是菱形( )
(5)对角线互相平分且邻边相等的四边形是菱形( )
(6)两组对边分别平行且一组邻边相等的四边形是菱形( )
×
√
×
×
√
√
2.□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形.
菱
矩
矩
菱
3.如图,在 ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵DE=BF,∴AE=CF,
∵AE∥CF,∴四边形AECF是平行四边形,∵AC⊥EF,∴平行四边形AECF是菱形
4.如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
(1)证明:∵AD∥BC,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AD=AB,
∵BA=BC,
∴AD=BC,
∴四边形ABCD是平行四边形,
∵BA=BC,
∴四边形ABCD是菱形;
(2)解:∵DE⊥BD,∴∠BDE=90°,
∴∠DBC+∠E=∠BDC+∠CDE=90°,
∵CB=CD,∴∠DBC=∠BDC,
∴∠CDE=∠E,
∴CD=CE=BC,
∴BE=2BC=10,
∵BD=8,
∴DE= =6,
∵四边形ABCD是菱形,
∴AD=AB=BC=5,
∴四边形ABED的周长=AD+AB+BE+DE=26.
课堂总结
四条边都相等
菱形
一组邻边相等
对角线互相垂直
对角线互相平分
一组对边平行且相等
两组对边分别平行或相等
四边形
平行四边形
两组对角分别相等
每条对角线平分一组对角
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
19.2.2菱形的判定
华师大版 八年级 下册
教学目标
教学目标:1.经历菱形判定定理的探究过程,掌握菱形的判定定理.
2.会用这些菱形的判定方法进行有关的证明和计算.
教学重点:菱形判定定理的掌握和应用.
教学难点:菱形判定定理的灵活应用.
-----我知道的四边形、平行四边形、矩形与菱形
平行四边形
A
B
C
D
四边形
A
B
C
D
AD//BC
DC//AB
一般
特殊
有一个角是直角
A
B
C
D
矩形
邻边相等
D
A
B
C
菱形
那如何判定一个四边形或平行四边形是菱形呢?你是怎样考虑的?
新知导入
情境引入
1.定义:一组邻边相等的平行四边形叫做菱形.
菱形的定义作为我们判定菱形的基本方法,接下来我们从边上来研究菱形的判定方法.
∵四边形ABCD是平行四边形,AB=AD.
∴四边形ABCD是菱形.
数学语言
四条边相等的四边形是菱形.
菱形的四条边相等.
逆命题
这个逆命题成立吗?
新知讲解
合作学习
试一试
如图,作一个四条边都相等的四边形.
1.画两条相等的线段AB、AD;
2.分别以点B和点D为圆心、AB长为半径画弧,两弧相交于点C
3.连结BC、CD,即得一个四条边都相等的四边形ABCD.
A
B
D
C
观察你所画的图形,它是菱形吗?
所画图形是菱形
证一证
证明:∵AB=BC=CD=AD;
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
A
B
C
D
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
四条边都相等的四边形是菱形
AB=BC=CD=AD
几何语言:
∵在四边形ABCD中,AB=BC=CD=AD,
∴四边形 ABCD是菱形.
A
B
C
D
菱形ABCD
四边形ABCD
A
B
C
D
菱形的判定定理1:
思考
菱形的两条对角线互相垂直
这是菱形所特有的性质.你能从对角线的角度得到什么关于菱形判定的猜想?
猜想:对角线互相垂直的平行四边形是菱形.
试一试
前面我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形 对此你有什么猜想?
做一做
作一条两条对角线互相垂直的平行四边形.
步骤:
1.作两条互相垂直的直线m、n,记交点为点O;
2.以点 O为圆心、适当长为半径画弧,
在直线 m,n上分别截取相等的
两组线段OA、OC和OB、OD ;
3.连接A、B、C、D四点 ,显然,
它是一个对角线互相垂直的平行四边形.
m
n
O
A
B
C
D
提炼概念
对角线互相垂直的平行四边形是菱形.
AC⊥BD
几何语言:
∵在□ABCD中,AC⊥BD,
∴ □ABCD是菱形.
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
菱形的判定定理2:
典例精讲
例4 如图,在矩形ABCD中,点E、F、G、H分别是四条边的中点,试问四边形EFGH是什么图形?并说明理由.
解:∵H点为AD的中点,∴AH=HD,
∵E点为AB的中点,AE= AB,
G点为DC的中点,DG= CD ,
又∵AB=DC,∴AE=DG.
∵∠HAE=∠HDG,∴△EAH≌△GDH , ∴HE=HG ,
同理EF=FG=HG=HE ,
∴四边形EFGH是菱形.
例5 如图,已知矩形ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F.
求证:四边形AFCE是菱形.
分析:要证四边形AFCE是菱形,由已知条件可知EF⊥AC,所以只需证明四边形AFCE是平行四边形,又知EF垂直平分AC,所以只需证明OE=OF.
证明:∵四边形ABCD是矩形,∴AE∥FC,
∴∠1=∠2.
∵EF平分AC,∴OA=OC.
又∵∠AOE=∠COF=90°,
∴△AOE≌△COF, ∴OE=OF,
∴四边形AFCE是平行四边形.
又∵EF⊥AC,
∴四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).
归纳概念
定义:有一组邻边相等的平行四边形叫做菱形
判定定理1:四边都相等的四边形是菱形
菱形的判定
对角线互相垂直的平行四边形是菱形.
课堂练习
1、判断题
(1)对角线互相垂直的四边形是菱形( )
(2)一条对角线垂直另一条对角线的四边形是菱形( )
(3)对角线互相垂直且平分的四边形是菱形( )
(4)对角线相等的四边形是菱形( )
(5)对角线互相平分且邻边相等的四边形是菱形( )
(6)两组对边分别平行且一组邻边相等的四边形是菱形( )
×
√
×
×
√
√
2.□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形;
(2)若AC=BD,则□ABCD是 形;
(3)若∠ABC是直角,则□ABCD是 形;
(4)若∠BAO=∠DAO,则□ABCD是 形.
菱
矩
矩
菱
3.如图,在 ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵DE=BF,∴AE=CF,
∵AE∥CF,∴四边形AECF是平行四边形,∵AC⊥EF,∴平行四边形AECF是菱形
4.如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
(1)证明:∵AD∥BC,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AD=AB,
∵BA=BC,
∴AD=BC,
∴四边形ABCD是平行四边形,
∵BA=BC,
∴四边形ABCD是菱形;
(2)解:∵DE⊥BD,∴∠BDE=90°,
∴∠DBC+∠E=∠BDC+∠CDE=90°,
∵CB=CD,∴∠DBC=∠BDC,
∴∠CDE=∠E,
∴CD=CE=BC,
∴BE=2BC=10,
∵BD=8,
∴DE= =6,
∵四边形ABCD是菱形,
∴AD=AB=BC=5,
∴四边形ABED的周长=AD+AB+BE+DE=26.
课堂总结
四条边都相等
菱形
一组邻边相等
对角线互相垂直
对角线互相平分
一组对边平行且相等
两组对边分别平行或相等
四边形
平行四边形
两组对角分别相等
每条对角线平分一组对角
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
