18.1 变量与函数(2)[下学期]
文档属性
| 名称 | 18.1 变量与函数(2)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 465.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-26 00:00:00 | ||
图片预览







文档简介
课件21张PPT。118.1变量与函数(2)2一般地,在一个变化过程中有两个变量x与y,如果对于x每 一个值,y都有唯一的值与它对应,那么就说x是
自变量,y是因变量,此时也称 y是x的函数。 函数 1.函数概念包含:(1)两个变量;(2)两个变量之间的对应关系.34试一试:看谁的眼光准例1、判断下列变量关系是不是函数?(1)等腰三角形的底边长与面积判断是不是函数,我们可以看它的数学式子中的变量之间是否满足函数的定义5函数关系式 用来表示函数关系的等式叫做函数关系式,也称为函数的解析式。6函数的关系式是等式
那么函数解析式的书写有没有要求呢? 通常等式的右边是含有自变量的代数
式,左边的一个字母表示函数如何去书写呢?7根据所给的 条件,写出y与x的函数关系式:矩形的周长是18 cm ,它的长是
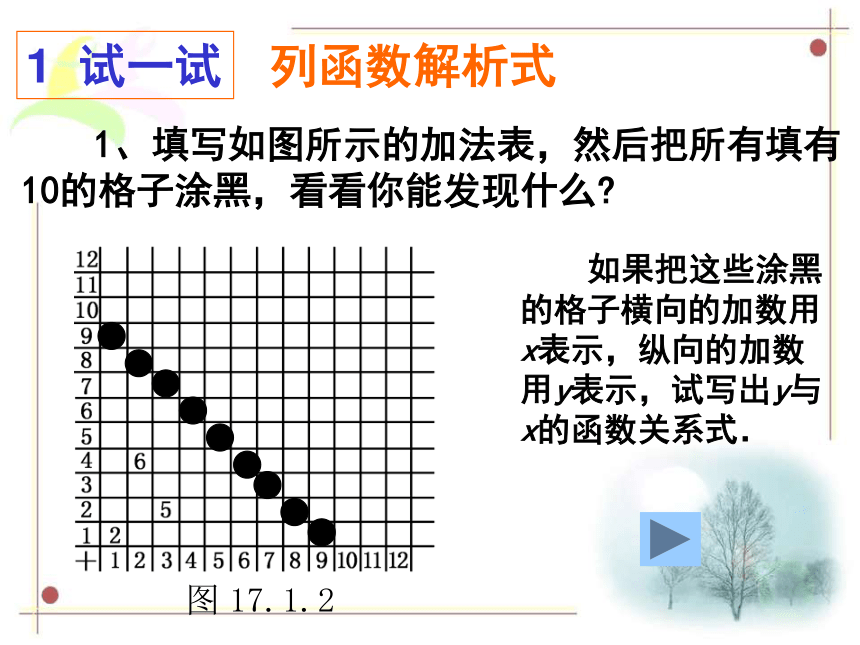
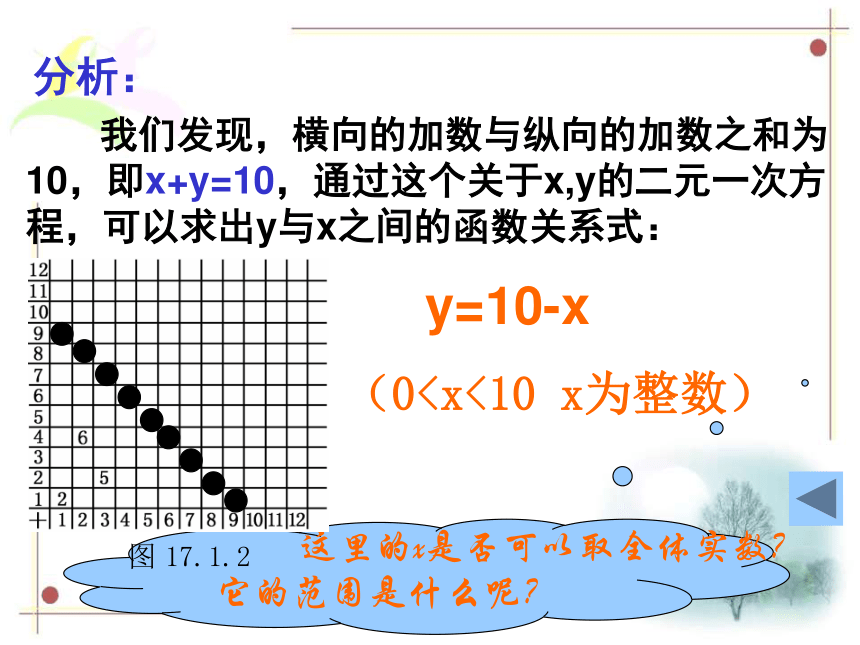
y cm ,宽是x cm ;8列函数解析式 1、填写如图所示的加法表,然后把所有填有10的格子涂黑,看看你能发现什么?1 试一试 如果把这些涂黑的格子横向的加数用x表示,纵向的加数用y表示,试写出y与x的函数关系式.9分析: 我们发现,横向的加数与纵向的加数之和为10,即x+y=10,通过这个关于x,y的二元一次方程,可以求出y与x之间的函数关系式: 这里的x是否可以取全体实数?它的范围是什么呢?y=10-x(0全体,叫做函数自变量的取值范围。13例1 求下列函数中自变量x的取值范围分析:用数学式子表示的函数,一般来说,自变量只能取使式子有意义的值。(4)因为被开方式必须为非负数才有意义,所以 ,自变量x的取值范围是 。解: (1) x取任意实数(2) x取任意实数(3)因为x=-2时,分式分母为0,没有意义,所以x取不等于-2的任意实数(可表示为 x≠-2)14函数解析式是数学式子的自变量取值范围: 1、当函数解析式是只含有一个自变量的整式时,
2、当函数解析式是分式时,
3、当函数解析式是二次根式时,自变量的取值范围是全体实数自变量的取值范围是使分母不为零的实数自变量的取值范围是使被开方数不小于零的实数15实际问题的函数解析式中自变量取值范围:1 函数自变量的取值范围既要使实际问题有意义,又要同时满足解析式的数学意义。2 实际问题有意义主要指的是:
(1)问题的实际背景(例如自变量表示人数时,应为非负整数等)
(2) 保证几何图形存在(例如等腰三角形底角大于0度小于90度等)16练习: 1 求下列函数中自变量x的取值范围17练习:求下列函数中自变量x的取值范围183、如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10 cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分面积ycm2与MA长度x cm之间的函数关系式. xy19小结:函数 如果在一个变化过程中,有两个变量x与y,对于x的每一个确定的值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量,y是x的函数. 1 函数的定义3 求函数解析式的方法20小结:3 函数自变量的取值范围 使函数有意义的自变量的取值的
全体,叫做函数自变量的取值范围。4 求自变量取值范围的方法: 根据使函数表示的实际问题有意义的条件,以及使函数解析式中的数学式子有意义的条件,列出不等式或不等式组,求出它或它们的解集,即为自变量的取值范围。www.czsx.com.cn21 课本P44
练习第2、3题作业
自变量,y是因变量,此时也称 y是x的函数。 函数 1.函数概念包含:(1)两个变量;(2)两个变量之间的对应关系.34试一试:看谁的眼光准例1、判断下列变量关系是不是函数?(1)等腰三角形的底边长与面积判断是不是函数,我们可以看它的数学式子中的变量之间是否满足函数的定义5函数关系式 用来表示函数关系的等式叫做函数关系式,也称为函数的解析式。6函数的关系式是等式
那么函数解析式的书写有没有要求呢? 通常等式的右边是含有自变量的代数
式,左边的一个字母表示函数如何去书写呢?7根据所给的 条件,写出y与x的函数关系式:矩形的周长是18 cm ,它的长是
y cm ,宽是x cm ;8列函数解析式 1、填写如图所示的加法表,然后把所有填有10的格子涂黑,看看你能发现什么?1 试一试 如果把这些涂黑的格子横向的加数用x表示,纵向的加数用y表示,试写出y与x的函数关系式.9分析: 我们发现,横向的加数与纵向的加数之和为10,即x+y=10,通过这个关于x,y的二元一次方程,可以求出y与x之间的函数关系式: 这里的x是否可以取全体实数?它的范围是什么呢?y=10-x(0
2、当函数解析式是分式时,
3、当函数解析式是二次根式时,自变量的取值范围是全体实数自变量的取值范围是使分母不为零的实数自变量的取值范围是使被开方数不小于零的实数15实际问题的函数解析式中自变量取值范围:1 函数自变量的取值范围既要使实际问题有意义,又要同时满足解析式的数学意义。2 实际问题有意义主要指的是:
(1)问题的实际背景(例如自变量表示人数时,应为非负整数等)
(2) 保证几何图形存在(例如等腰三角形底角大于0度小于90度等)16练习: 1 求下列函数中自变量x的取值范围17练习:求下列函数中自变量x的取值范围183、如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10 cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分面积ycm2与MA长度x cm之间的函数关系式. xy19小结:函数 如果在一个变化过程中,有两个变量x与y,对于x的每一个确定的值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量,y是x的函数. 1 函数的定义3 求函数解析式的方法20小结:3 函数自变量的取值范围 使函数有意义的自变量的取值的
全体,叫做函数自变量的取值范围。4 求自变量取值范围的方法: 根据使函数表示的实际问题有意义的条件,以及使函数解析式中的数学式子有意义的条件,列出不等式或不等式组,求出它或它们的解集,即为自变量的取值范围。www.czsx.com.cn21 课本P44
练习第2、3题作业
