18.3 一次函数[下学期]
图片预览





文档简介
课件25张PPT。朋友很高兴和你一起学习上虞市沥海镇中 毛志兵一次函数(复习)
请同学们在同一坐标系中画出函数 y=2 x, y=2x+1, y=2 x-1的图象.一次函数:函数y=_______(k、b为常数,k______)叫做一次函数。
当b_____时,函数y=____(k____)叫做正比例函数。
kx +b≠0=0kx≠0★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。1K≠0■知识链接
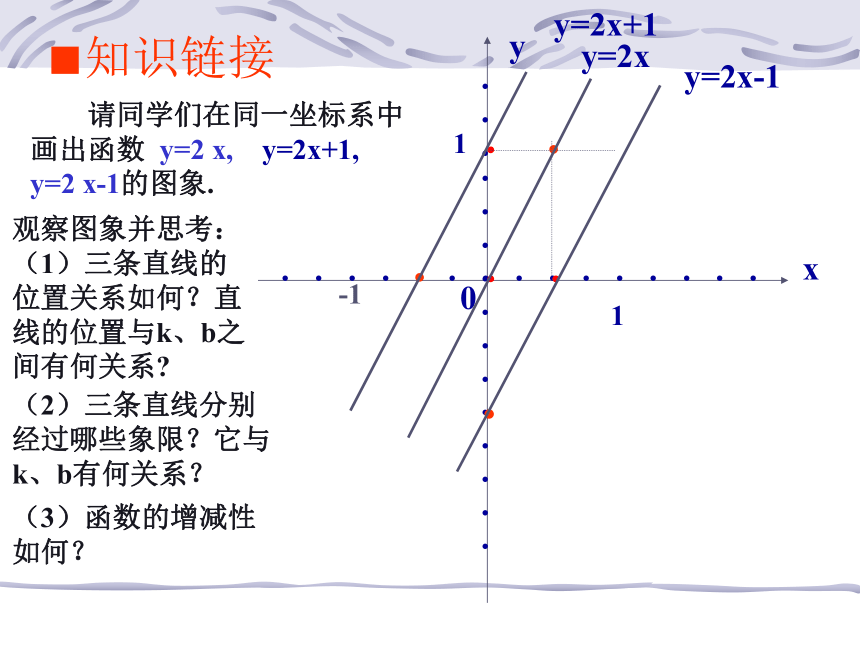
···11.-1..y=2x+1y=2x y=2x-1 请同学们在同一坐标系中画出函数 y=2 x, y=2x+1, y=2 x-1的图象.
(3)函数的增减性如何?
观察图象并思考:
(1)三条直线的位置关系如何?直线的位置与k、b之间有何关系?
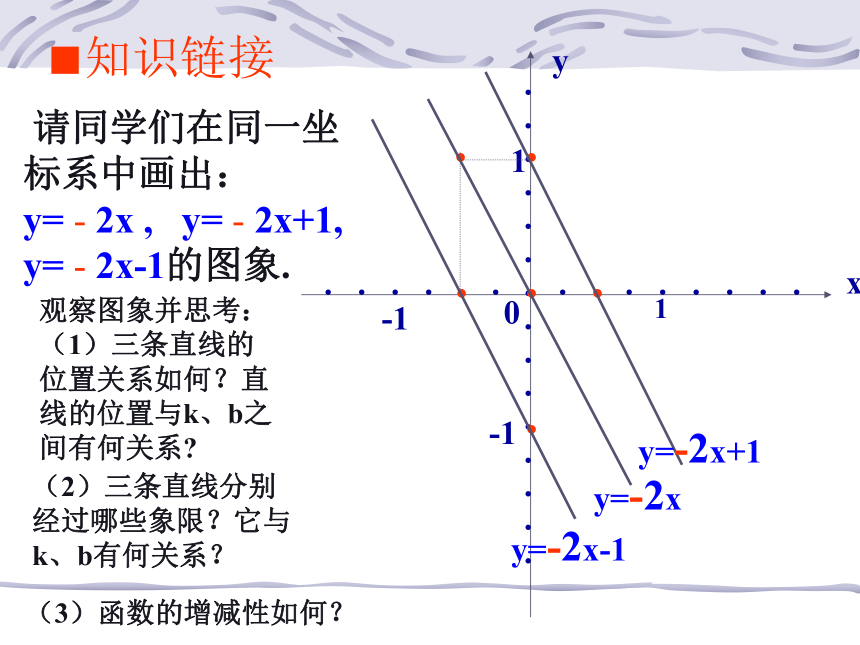
(2)三条直线分别经过哪些象限?它与k、b有何关系?■知识链接1...1.-1.-1. 请同学们在同一坐标系中画出:
y= - 2x , y= - 2x+1,
y= - 2x-1的图象.
y=-2x+1y=-2x y=-2x-1观察图象并思考:
(1)三条直线的位置关系如何?直线的位置与k、b之间有何关系?
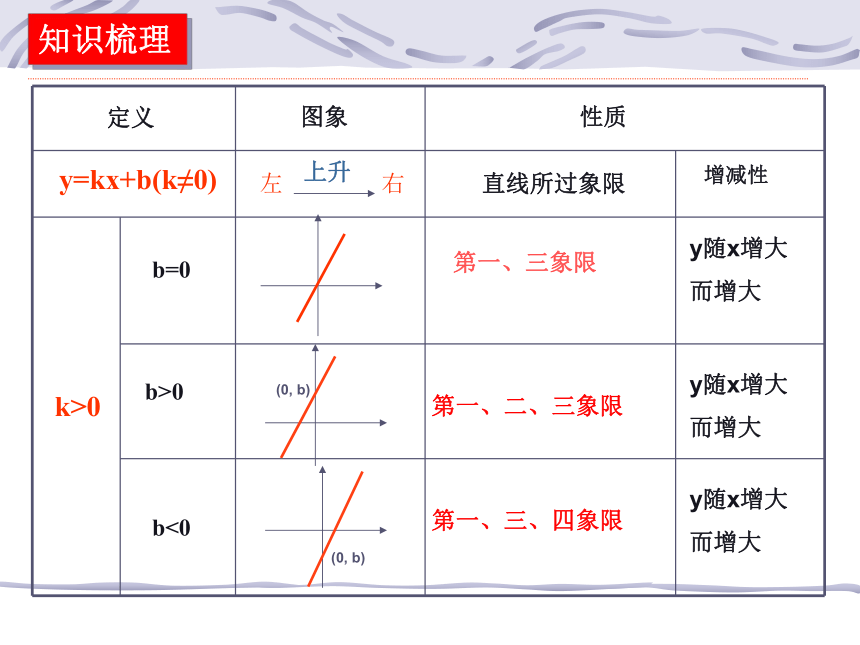
(2)三条直线分别经过哪些象限?它与k、b有何关系?(3)函数的增减性如何?■知识链接定义图象性质y=kx+b(k≠0)b=0b>0b<0k>0直线所过象限增减性上升第一、三象限第一、二、三象限第一、三、四象限y随x增大
而增大 y随x增大
而增大 y随x增大
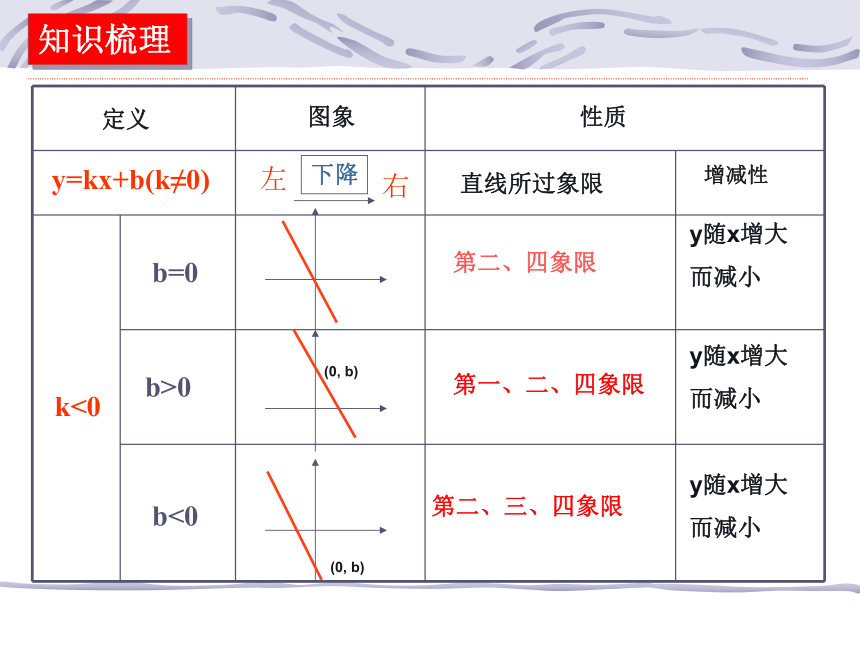
而增大 知识梳理定义图象性质y=kx+b(k≠0)b=0b>0b<0k<0直线所过象限增减性下降第二、四象限第一、二、四象限第二、三、四象限y随x增大
而减小 y随x增大
而减小y随x增大
而减小知识梳理小 试 牛 刀②①、②、③④③小 试 牛 刀C2、直线y=2x―4与x轴的交点坐标是 ,与y轴
的交点坐标是 ,直线与两坐标轴围成的三角
形的面积是 。(2,0)( 0, - 4)4小 试 牛 刀 4.已知一次函数y=kx+b , y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
(A) (B) (C) (D)A小 试 牛 刀 5、一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是( )A小 试 牛 刀 哇!!同学们好厉害哦!! 6、一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系式的图象是( )D 【例 1】已知:函数 y = (m+1) x + 2 m﹣6
(1)若函数图象过(﹣1 ,2),求此函数的解析式。
(2)若函数图象与直线 y = 2 x + 5 平行,求其函数的解析式。
(3)求满足(2)条件的直线与直线 y = ﹣3 x + 1 的交点,并
求这两条直线 与y 轴所围成的三角形面积 . 解:(1)由题意:
2=﹣(m+1)+2m﹣6解得 m = 9(2) 由题意,m +1= 2
解得 m = 1
∴ y = 2x﹣4(3) 由题意得∴ 这两直线的交点是(1 ,﹣2)y = 2x﹣4 与y 轴交于( 0 , - 4 )
y = ﹣3x + 1与y 轴交于( 0 , 1)●11-4(1, ﹣2)S△=-2∴ y = 10x+12
【例 2】下图 l1 l2 分别是龟兔赛跑中路程与时间之间的函数图象。做一做
新龟兔赛跑 s /米(1)这一次是 米赛跑。12345O10020120406080t /分687(2)表示兔子的图象是 。-11291011-3-2100l2-4根据图象可以知道:s /米(3)当兔子到达终点时,乌龟距终点还有 米。l1l212345O10020120406080t /分687(4)乌龟要与兔子同时到达终点乌龟要先跑 米。(5)乌龟要先到达终点,至少要比兔子早跑 分钟。-11291011-3-2404-440【例 3】某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。(1)分别求出0≤ x ≤2 和x≥2时y与x之间的函数关系式;
生活中的数学解:(1)当0≤ x ≤2时,设y=kx(k≠0)因图象过点(2,6),代入得6=2k, k=3∴y=3x当x ≥ 2时, 设y=kx+b(k≠0)因图象过点(2,6)及点(10,3),代入得解得(2)如果每毫升血液中含药量为4微克或4微克以上时,治疗疾病有效,那么这个有效时间是多长?
生活中的数学当x ≤2时, y=3x;
当x ≥ 2时, 解:当y=4时,由y=3x , 得所以使用该种新药的有效时间是6小时.4x1x2【例4】某空军加油机接到命令,立即给一架正在飞行的运输飞机进行空中加油,在加油过程中,设运输机的油箱余油量为Q1吨,加油飞机的加油油箱余油量为Q2吨,加油时间为t分钟,Q1、Q2与t之间的函数图像如图所示,结合图像回答下列问题:
(1)加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需多少分钟?
解:(1)由图像知,加油飞机的加
油箱中装载了30吨油,全部
加给运输飞机需10分钟 ;(3)运输飞机加完油后,以原速继续飞行,需10小时到达目的地,油料是否够用?说明理由.解:(3)根据图像可知
运输飞机的耗油量为每分钟0.1吨.∴10小时耗油量为:
10×60×0.1=60吨∴油够用.<69吨.(2)求加油过程中,运输飞机的余油量Q1(吨)与时间t(分)的函数关系式.解:(2)因图象过点(0 , 40)及点(10 , 6 9 ),代入得所以 Q1=2.9t+40 (0≤t≤10) 一路下来,大家收获不小吧!说说你的感受,让大家一起来分享,好吗?…… 今天我们一起回顾了哪些知识?你还有哪些困惑?你对老师有哪些意见和建议?老师建议: 1.结合具体情景体会一次函数的意义,
2.会画一次函数的图象(注意:实际问题中的图象往往是一条线段,甚至是一些离散的点),掌握一次函数图象的分布规律.
3.能从图象中获取信息(注意弄清楚坐标轴的意义,抓住一些关键性的点)。
4.能结合图象理解一次函数的性质;
5.能用待定系数法求一次函数的解析式;
6.能用一次函数解决一些实际问题。
小明在电信局办理了某种电话话费套餐,该套餐要求按分钟计费且无论通话多长时间都需要交纳一定的费用作为月租费,办理后某月手机话费y元和通话时间x的关系图如下:观察图象形状,有何特点,你知道该电话套餐的内容吗? ⑴该话费套餐的月租费是多少元?⑵每分钟通话需多少元?100分钟后每分钟通话: 100分钟前每分钟通话: 如图,l甲、l乙两条直线分别表示甲走路与乙骑车(在同一条路上)行走的路程S与时间t的关系,根据此图,回答下列问题:1)乙出发时,与甲相距 km2)行走一段时间后,乙的自行车发生故障停下来修理,修车时间为 h3)乙从出发起,经过 h与甲相遇;4)甲的速度为 km/h , 乙的速度为 km/h5)甲行走的路程s(千米)与时间t(小时)之间的函数关系式是 6)如果乙的自行车不出故障,则乙出发后经过 h与甲相遇,相遇后离乙的出发点 km,并在图中标出其相遇点。1012.5515s=5t+10(t≥0)115A相遇点为A应用拓展祝学有所获
请同学们在同一坐标系中画出函数 y=2 x, y=2x+1, y=2 x-1的图象.一次函数:函数y=_______(k、b为常数,k______)叫做一次函数。
当b_____时,函数y=____(k____)叫做正比例函数。
kx +b≠0=0kx≠0★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,
⑵、比例系数_____。1K≠0■知识链接
···11.-1..y=2x+1y=2x y=2x-1 请同学们在同一坐标系中画出函数 y=2 x, y=2x+1, y=2 x-1的图象.
(3)函数的增减性如何?
观察图象并思考:
(1)三条直线的位置关系如何?直线的位置与k、b之间有何关系?
(2)三条直线分别经过哪些象限?它与k、b有何关系?■知识链接1...1.-1.-1. 请同学们在同一坐标系中画出:
y= - 2x , y= - 2x+1,
y= - 2x-1的图象.
y=-2x+1y=-2x y=-2x-1观察图象并思考:
(1)三条直线的位置关系如何?直线的位置与k、b之间有何关系?
(2)三条直线分别经过哪些象限?它与k、b有何关系?(3)函数的增减性如何?■知识链接定义图象性质y=kx+b(k≠0)b=0b>0b<0k>0直线所过象限增减性上升第一、三象限第一、二、三象限第一、三、四象限y随x增大
而增大 y随x增大
而增大 y随x增大
而增大 知识梳理定义图象性质y=kx+b(k≠0)b=0b>0b<0k<0直线所过象限增减性下降第二、四象限第一、二、四象限第二、三、四象限y随x增大
而减小 y随x增大
而减小y随x增大
而减小知识梳理小 试 牛 刀②①、②、③④③小 试 牛 刀C2、直线y=2x―4与x轴的交点坐标是 ,与y轴
的交点坐标是 ,直线与两坐标轴围成的三角
形的面积是 。(2,0)( 0, - 4)4小 试 牛 刀 4.已知一次函数y=kx+b , y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
(A) (B) (C) (D)A小 试 牛 刀 5、一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是( )A小 试 牛 刀 哇!!同学们好厉害哦!! 6、一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系式的图象是( )D 【例 1】已知:函数 y = (m+1) x + 2 m﹣6
(1)若函数图象过(﹣1 ,2),求此函数的解析式。
(2)若函数图象与直线 y = 2 x + 5 平行,求其函数的解析式。
(3)求满足(2)条件的直线与直线 y = ﹣3 x + 1 的交点,并
求这两条直线 与y 轴所围成的三角形面积 . 解:(1)由题意:
2=﹣(m+1)+2m﹣6解得 m = 9(2) 由题意,m +1= 2
解得 m = 1
∴ y = 2x﹣4(3) 由题意得∴ 这两直线的交点是(1 ,﹣2)y = 2x﹣4 与y 轴交于( 0 , - 4 )
y = ﹣3x + 1与y 轴交于( 0 , 1)●11-4(1, ﹣2)S△=-2∴ y = 10x+12
【例 2】下图 l1 l2 分别是龟兔赛跑中路程与时间之间的函数图象。做一做
新龟兔赛跑 s /米(1)这一次是 米赛跑。12345O10020120406080t /分687(2)表示兔子的图象是 。-11291011-3-2100l2-4根据图象可以知道:s /米(3)当兔子到达终点时,乌龟距终点还有 米。l1l212345O10020120406080t /分687(4)乌龟要与兔子同时到达终点乌龟要先跑 米。(5)乌龟要先到达终点,至少要比兔子早跑 分钟。-11291011-3-2404-440【例 3】某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。(1)分别求出0≤ x ≤2 和x≥2时y与x之间的函数关系式;
生活中的数学解:(1)当0≤ x ≤2时,设y=kx(k≠0)因图象过点(2,6),代入得6=2k, k=3∴y=3x当x ≥ 2时, 设y=kx+b(k≠0)因图象过点(2,6)及点(10,3),代入得解得(2)如果每毫升血液中含药量为4微克或4微克以上时,治疗疾病有效,那么这个有效时间是多长?
生活中的数学当x ≤2时, y=3x;
当x ≥ 2时, 解:当y=4时,由y=3x , 得所以使用该种新药的有效时间是6小时.4x1x2【例4】某空军加油机接到命令,立即给一架正在飞行的运输飞机进行空中加油,在加油过程中,设运输机的油箱余油量为Q1吨,加油飞机的加油油箱余油量为Q2吨,加油时间为t分钟,Q1、Q2与t之间的函数图像如图所示,结合图像回答下列问题:
(1)加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需多少分钟?
解:(1)由图像知,加油飞机的加
油箱中装载了30吨油,全部
加给运输飞机需10分钟 ;(3)运输飞机加完油后,以原速继续飞行,需10小时到达目的地,油料是否够用?说明理由.解:(3)根据图像可知
运输飞机的耗油量为每分钟0.1吨.∴10小时耗油量为:
10×60×0.1=60吨∴油够用.<69吨.(2)求加油过程中,运输飞机的余油量Q1(吨)与时间t(分)的函数关系式.解:(2)因图象过点(0 , 40)及点(10 , 6 9 ),代入得所以 Q1=2.9t+40 (0≤t≤10) 一路下来,大家收获不小吧!说说你的感受,让大家一起来分享,好吗?…… 今天我们一起回顾了哪些知识?你还有哪些困惑?你对老师有哪些意见和建议?老师建议: 1.结合具体情景体会一次函数的意义,
2.会画一次函数的图象(注意:实际问题中的图象往往是一条线段,甚至是一些离散的点),掌握一次函数图象的分布规律.
3.能从图象中获取信息(注意弄清楚坐标轴的意义,抓住一些关键性的点)。
4.能结合图象理解一次函数的性质;
5.能用待定系数法求一次函数的解析式;
6.能用一次函数解决一些实际问题。
小明在电信局办理了某种电话话费套餐,该套餐要求按分钟计费且无论通话多长时间都需要交纳一定的费用作为月租费,办理后某月手机话费y元和通话时间x的关系图如下:观察图象形状,有何特点,你知道该电话套餐的内容吗? ⑴该话费套餐的月租费是多少元?⑵每分钟通话需多少元?100分钟后每分钟通话: 100分钟前每分钟通话: 如图,l甲、l乙两条直线分别表示甲走路与乙骑车(在同一条路上)行走的路程S与时间t的关系,根据此图,回答下列问题:1)乙出发时,与甲相距 km2)行走一段时间后,乙的自行车发生故障停下来修理,修车时间为 h3)乙从出发起,经过 h与甲相遇;4)甲的速度为 km/h , 乙的速度为 km/h5)甲行走的路程s(千米)与时间t(小时)之间的函数关系式是 6)如果乙的自行车不出故障,则乙出发后经过 h与甲相遇,相遇后离乙的出发点 km,并在图中标出其相遇点。1012.5515s=5t+10(t≥0)115A相遇点为A应用拓展祝学有所获
