18.3 一次函数[下学期]
图片预览





文档简介
课件48张PPT。数学组2005年3月一次函数复习一、知识要点: 1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。kx +b≠0=0≠0kx★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,⑵、比例系数_____。1k≠0 2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。0,01,k 一条直线b一条直线4.正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。一、三增大二、四减小5、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
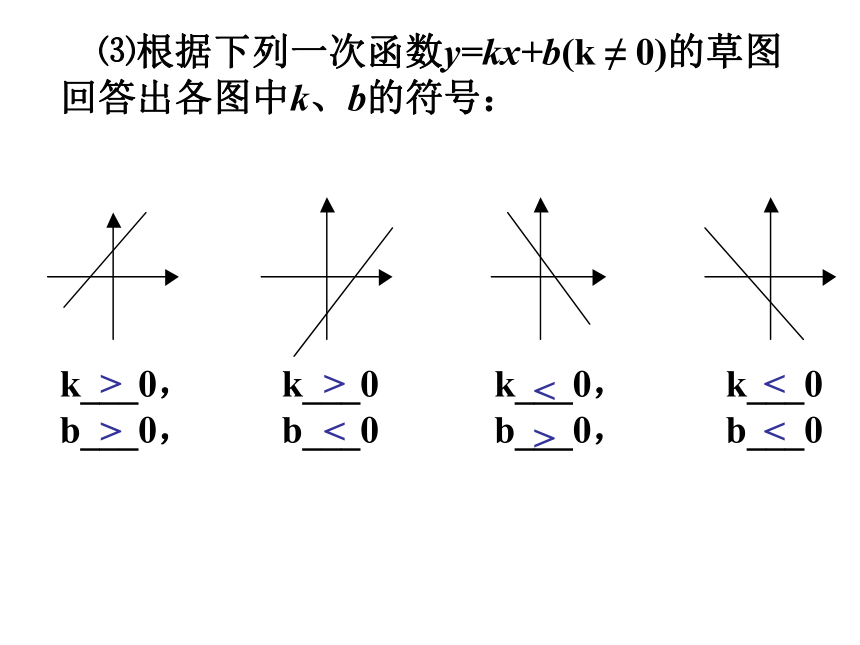
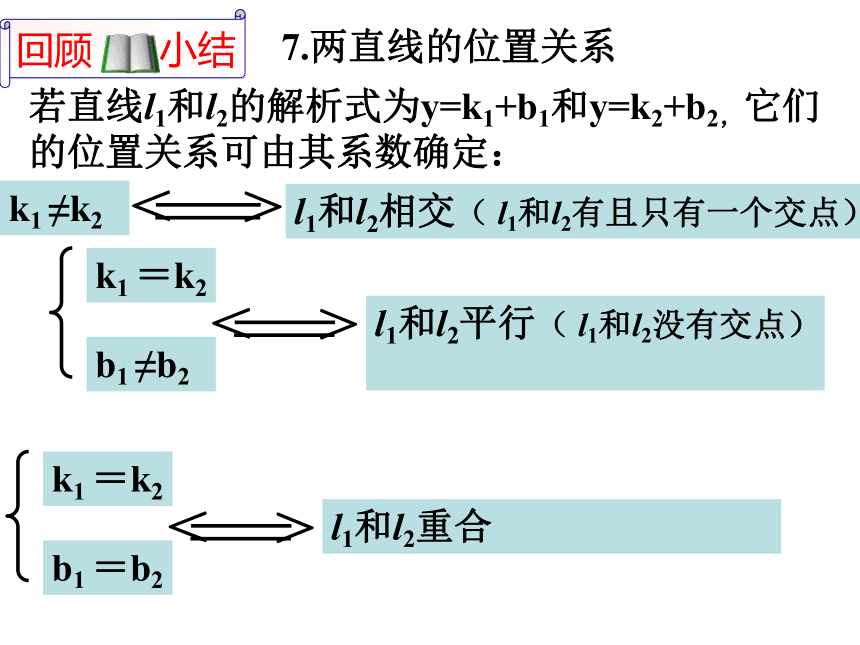
⑵当k<0时,y随x的增大而_________。增大减小 ⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:k___0, k___0 k___0, k___0 b___0, b___0 b___0, b___0<<><<>>>7.两直线的位置关系若直线l1和l2的解析式为y=k1+b1和y=k2+b2,它们的位置关系可由其系数确定:6.当两个一次函数,k一样,b不一样时 ,它们的图象( )
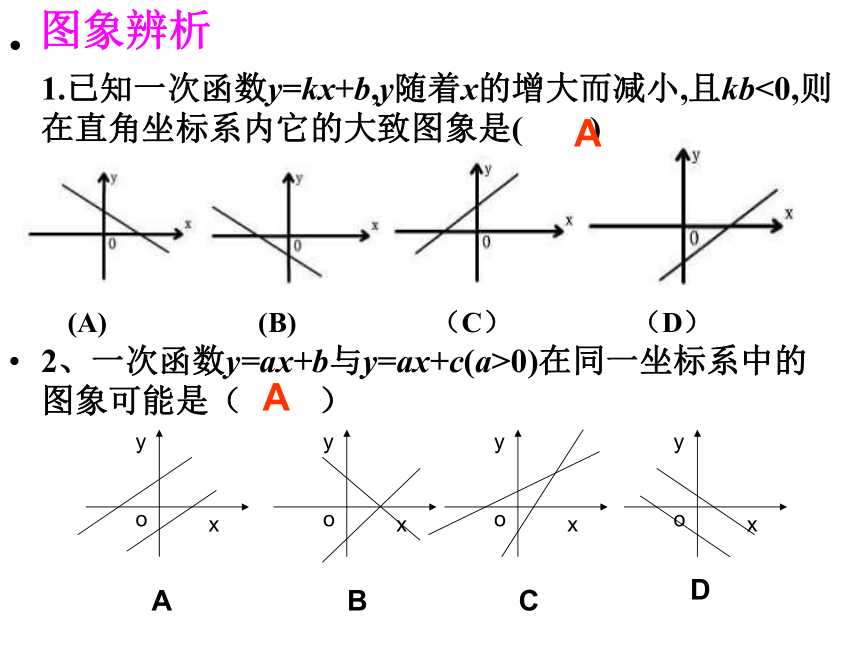
,两个一次函数,当b一样,k不一样时它们的图象( ) .7.求两个一次函数图象的交点方法( )或( )互相平行的两条直线图象法解方程组法交y轴与( 0,b)2、一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是( ) 1.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
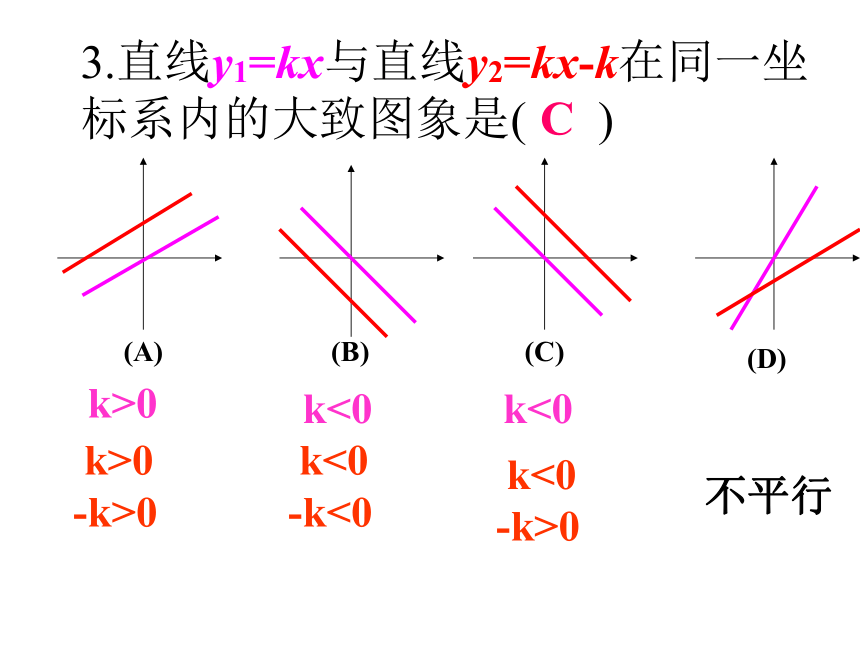
(A) (B) (C) (D)A图象辨析A3.直线y1=kx与直线y2=kx-k在同一坐标系内的大致图象是( )k>0k<0k<0不平行
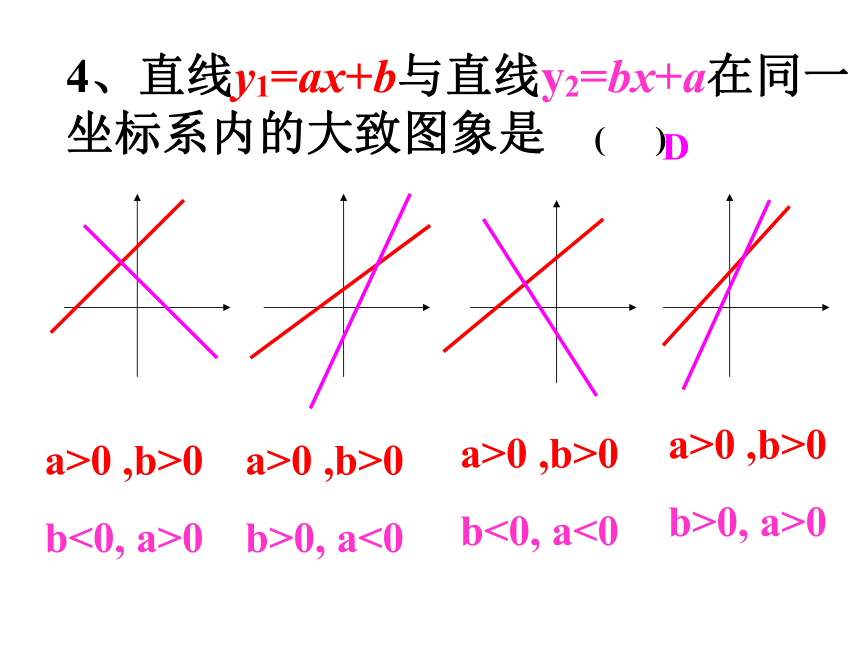
k>0 -k>0 k<0 -k<0 k<0 -k>0C4、直线y1=ax+b与直线y2=bx+a在同一坐标系内的大致图象是 ( )
a>0 ,b>0
b<0, a>0
a>0 ,b>0
b>0, a<0
a>0 ,b>0
b<0, a<0
a>0 ,b>0
b>0, a>0D4. 如图,在同一坐标系中,关于x的一次函数 y=x+b与y=bx+1的图象只可能是( )C 一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系的图象是( ) 选
一
选ACBDD利用数学 走近生活一、火车站托运行李费用与托运行李的重量关系如图所示。(1)当x=30时,y=_______; 当x=_______,y=30。(2)你能确定该关系所在直线的函数解析式吗?(3)当货物少于 千克,可免费托运。204010y=x-10 4、 下图 l1 l2 分别是龟兔赛跑中路程与时间之间的函数图象。做一做
新龟兔赛跑 s /米(1)这一次是 米赛跑。12345O10020120406080t /分687(2)表示兔子的图象是 。-11291011-3-2100l2-4根据图象可以知道:s /米(3)当兔子到达终点时,乌龟距终点还有 米。l1l212345O10020120406080t /分687(4)乌龟要与兔子同时到达终点乌龟要先跑 米。(5)乌龟要先到达终点,至少要比兔子早跑 分钟。-11291011-3-2404-4你还能用其他方法解决上述问题吗?40二、我国很多城市水资源缺乏,为了加强居民的节水意识,雉城镇制定了每月用水4吨以内(包括4吨)和用水4吨以上两种收费标准(收费标准:指每吨水的价格),用户每月应交水费y(元)是用水量x(吨)的函数,其函数图象如图所示。(1)观察图象,求出函数在不同范围内的解析式;
说出自来水公司在这两个用水范围内的收费标准;(2)若一用户5月份交水费12.8元,求他用了多少吨水? 2、某植物t天后的高度为ycm,图中反映了y与t之间的关系,根据图象回答下列问题:(1)植物刚栽的时候多高?9631215182124l2468101214t/天Y cm(2)3天后该植物高度为多少?(3)几天后该植物高度可达21cm?(4)先写出y与t的关系式,
再计算长到100cm需几天?初生牛犊不怕虎 小明在电信局办理了某种电话话费套餐,该套餐要求按分钟计费且无论通话多长时间都需要交纳一定的费用作为月租费,办理后某月手机话费y元和通话时间x的关系图如下:观察图象形状,有何特点,你知道该电话套餐的内容吗? ⑴该话费套餐的月租费是多少元?⑵每分钟通话需多少元?100分钟后每分钟通话: 100分钟前每分钟通话: 思考:1011121314课本36页第10题图中的折线表示一骑车人离家的距离Y与时间X的关系,骑车人9点离开家,15点回家,请你根据这个折线表示他的行程过程.(1)12:30分到13:30分离家最远,
这时他离家45千米。·(2)10:30他开始第一次休息,
休息了30分钟,
这时他离家30千米。(3)11:00到12:30他骑了15千米。(4)他在9:00到10:30的平均速度是20千米/时。(4)他在9:00到10:30的平均速度是20千米/时;
他在10:30到12:30的平均速度是7.5千米/时。(5)他返家时的平均速度是30千米/时。(6)14:00时他离家18千米;··
9:30和 时他距家10千米(6)14:00时他离家18千米;1015、某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(1)服药后______时,血液中含药量最高,
达到每毫升_______毫克,接着逐步衰弱。
(2)服药5时,血液中含药量为每毫升____毫克。
(3)当x≤2时y与x之间的函数关系式是_____。
(4)当x≥2时y与x之间的函数关系式是____。
(5)如果每毫升血液中含药量3毫克或3毫克以上
时,治疗疾病最有效,那么这个有效时间范围是___时。.(1)服药后______时,血液中含药量最高,
达到每毫升_______毫克,接着逐步衰弱。
(2)服药10时,血液中含药量为每毫升____毫克。
(3)当x≤2时y与x之间的函数关系式是___________
(4)当x≥2时y与x之间的函数关系式是___________
(5)如果每毫升血液中含药量3毫克或3毫克以上
时,治疗疾病最有效,那么这个有效时间范围是___时。
2603y=3x (x≤2)y=-x+8 (x≥2)5例1: 根据图象,求出相应的函数解析式:3 已知函数(1)当x=0时, y =(2 )当x=2时, y=
(3)当y=0时, x=
(4)当y>0时, x的取值范围 是(6)当-3≤y≤0时, x的取值范围 是(5)当y<1 时, x的取值范围是-311.5X>1.5x<20 ≤ x ≤ 1.51.5例5、已知一次函数图象是线段
1、自变量x的取值范围是
2、函数值y的取值范围是
3、图象与x轴交点为
图象与y轴交点为0≤x ≤6-1≤y ≤2( 4,0 )(0,2)4 、它的解析式为y = - 0.5x + 26、画出函数y=2x+1的图象,并利用图象求出下列题目1、当y≤3时,x的取值范围是多少?答:x≤12、当-3≤y<3时,x的取值范围是多少?答: -2≤x<1
练习 1. 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
(4)函数的图象过原点。
2.将直线y=3x-2向下平移6个单位,得到直线_____________________;
将直线y=-5x-5向上平移4个单位,得到直线_____________________.y=3x-8y=-5x-1一次函数y=b – 3x,y随x的增大而一次函数y= – 2x+b图象过(1, – 2),则b=一次函数y= –x+4的图象经过 象限直线y=kx+b经过一、二、三象限,那么y=bx –k经过 象限函数y=(m –2)x中,已知x1>x2时,y1y= 上,试比较a和b的大小.4.如图所示的图象分别给出了x与y的对应关系,其中y是x的函数的是( )2.甲、乙两地相距S千米,某人行完全程所用的时间t(时)与他的速度v(千米/时)满足vt=S,在这个变化过程中,下列判断中错误的是 ( )
A.S是变量 B.t是变量 C.v是变量 D.S是常量3.如图,足球由正五边形皮块(黑色)和正六边形皮块(白色)缝成,试用正六边形的块数x表示正五边形的块数y,并指出其中的变量和常量.(提示:每一个白色皮块周围连着三个黑色皮块)求直线y=2x-1与两坐标轴所围成的三角形面积y=2x-1 -1?解:(如图)∵当x=0时,y=-1 ∴ y=2x-1与y轴的交点为(0,-1) ∵当y=0时,x=?∴ y=2x-1与x轴的交点为(?,0)
= 1/4 ∴AO=? ,BO=1∴SΔAB0= ?·AO·BO = ?×?×1答:直线y=2x-1与两坐标轴所围成的三角形面积为1/4。 B A直线y=kx+3与两坐标轴所围成的三角形面积为9,求k的值y=kx+3 -3/k3解:(如图)∵当x=0时,y=3 ∴ y=kx+3与y轴的交点为(0,3) ∵当y=0时,x=-3/k∴ y=kx+3与x轴的交点为(-3/k,0)
∴ k=-1/2或k=1/2∴SΔAB0= ?·AO·BO=9 ?×3×|-3/k|=9答:k的值为-1/2或1/2 。 B A∴AO=3 ,BO=|-3/k|3.点P(x,y)在第一象限,且x+y=10,点A的坐标为
(8,0),设△OPA的面积为S。
(1)用含x的解析式表示S,写出x的取值范围,画出函数S的图象。·A·8PB(2)当S=12 时点P的坐标402、已知两条直线y1=2x-3和y2=5-x.
(1)在同一坐标系内作出它们的图象;
(2)求出它们的交点A的坐标;
(3)求出这两条直线与x轴围成的三角形ABC的面积. (2)因为A点同时在两条直线上,所以A点坐标同时满足这两个函数的解析式,即A点坐标就是方程组 点,则C(5,0). 老师给出一个函数,甲、乙、丙、丁各指出这个函数的一个性质:
甲:函数不经过第三象限
乙:函数经过第一象限
丙:当X<2时,Y>0
丁:当X <2时,Y随X的增大而减小
请根据以上信息构造一个函数想一想,议一议课堂小结:
1. 你对一次函数的知识都 熟悉了吗?
2. 通过今天的复习,现在会用一次函数的知识解决问题了吧!
3. 希望同学们对今 天复习的知识要十分熟练再见 1. 小星以2米/秒的速度起跑后,先匀速跑5秒,然后突然把速度提高4米/秒,又匀速跑5秒。试写出这段时间里他的跑步路程s(单位:米)随跑步时间x(单位:秒)变化的函数关系式,并画出函数图象。解:依题意得{
s=2x(0≤x≤5) s=10+6(x-5) (5(1)分别写出两个印刷厂的收费y(元)与印刷数量x(份)之间的函数关系式;
(2)印刷800份宣传材料,选择哪家印刷厂比较合算?
(3)如果只有3000元用于印刷宣传材料,找哪家印刷厂印制宣传材料能多一些?
探索与思考:已知反比例函数Y=K/2X(K≠0)和一次函数Y=2X-1,其中一次函数的图象经过(a, b),(a+1,b+k)两点。
(1)求反比例函数解析式。
(2)如图已知点A(m,1)在第一象限且同时在上述两个函数图象上求点A的坐标
(3)利用(2)的结果,请回答:
在X轴上是否存在点P使
△AOP为等腰三角形?若存在,
把符合条件的P点坐标都求出来,
若不存在,请说明理由。
⑴、解析式中自变量x的次数是___次,⑵、比例系数_____。1k≠0 2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。0,01,k 一条直线b一条直线4.正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。一、三增大二、四减小5、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。增大减小 ⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:k___0, k___0 k___0, k___0 b___0, b___0 b___0, b___0<<><<>>>7.两直线的位置关系若直线l1和l2的解析式为y=k1+b1和y=k2+b2,它们的位置关系可由其系数确定:6.当两个一次函数,k一样,b不一样时 ,它们的图象( )
,两个一次函数,当b一样,k不一样时它们的图象( ) .7.求两个一次函数图象的交点方法( )或( )互相平行的两条直线图象法解方程组法交y轴与( 0,b)2、一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是( ) 1.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
(A) (B) (C) (D)A图象辨析A3.直线y1=kx与直线y2=kx-k在同一坐标系内的大致图象是( )k>0k<0k<0不平行
k>0 -k>0 k<0 -k<0 k<0 -k>0C4、直线y1=ax+b与直线y2=bx+a在同一坐标系内的大致图象是 ( )
a>0 ,b>0
b<0, a>0
a>0 ,b>0
b>0, a<0
a>0 ,b>0
b<0, a<0
a>0 ,b>0
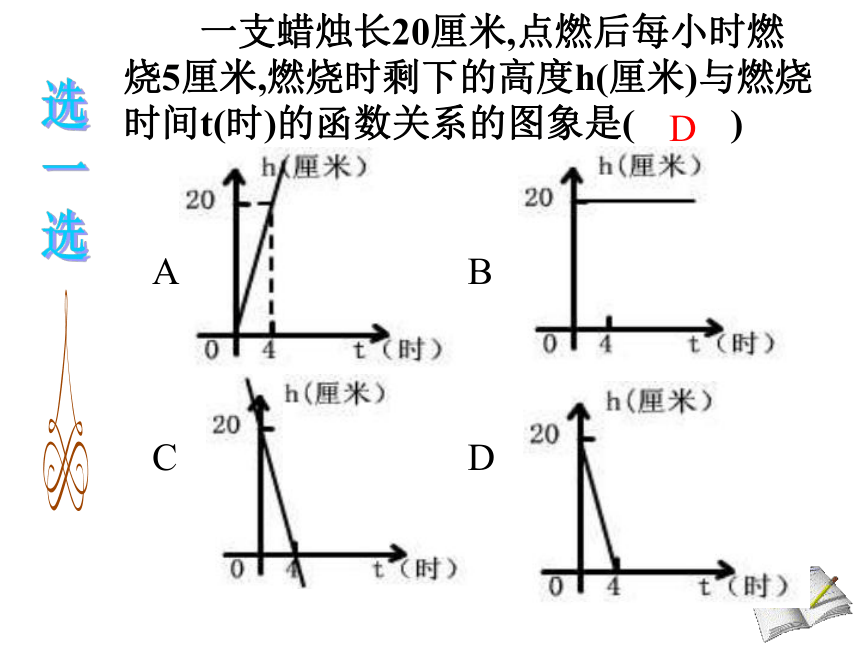
b>0, a>0D4. 如图,在同一坐标系中,关于x的一次函数 y=x+b与y=bx+1的图象只可能是( )C 一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系的图象是( ) 选
一
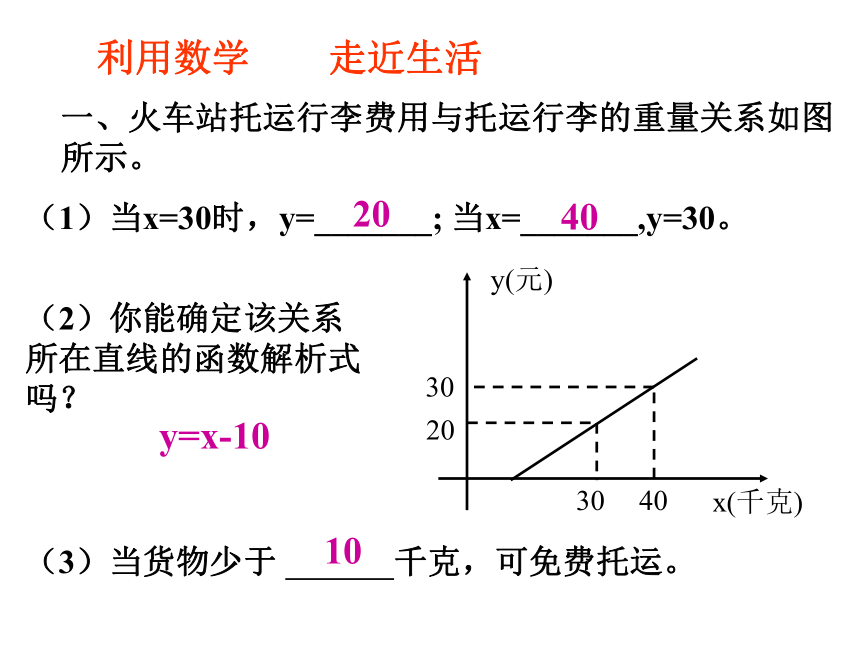
选ACBDD利用数学 走近生活一、火车站托运行李费用与托运行李的重量关系如图所示。(1)当x=30时,y=_______; 当x=_______,y=30。(2)你能确定该关系所在直线的函数解析式吗?(3)当货物少于 千克,可免费托运。204010y=x-10 4、 下图 l1 l2 分别是龟兔赛跑中路程与时间之间的函数图象。做一做
新龟兔赛跑 s /米(1)这一次是 米赛跑。12345O10020120406080t /分687(2)表示兔子的图象是 。-11291011-3-2100l2-4根据图象可以知道:s /米(3)当兔子到达终点时,乌龟距终点还有 米。l1l212345O10020120406080t /分687(4)乌龟要与兔子同时到达终点乌龟要先跑 米。(5)乌龟要先到达终点,至少要比兔子早跑 分钟。-11291011-3-2404-4你还能用其他方法解决上述问题吗?40二、我国很多城市水资源缺乏,为了加强居民的节水意识,雉城镇制定了每月用水4吨以内(包括4吨)和用水4吨以上两种收费标准(收费标准:指每吨水的价格),用户每月应交水费y(元)是用水量x(吨)的函数,其函数图象如图所示。(1)观察图象,求出函数在不同范围内的解析式;
说出自来水公司在这两个用水范围内的收费标准;(2)若一用户5月份交水费12.8元,求他用了多少吨水? 2、某植物t天后的高度为ycm,图中反映了y与t之间的关系,根据图象回答下列问题:(1)植物刚栽的时候多高?9631215182124l2468101214t/天Y cm(2)3天后该植物高度为多少?(3)几天后该植物高度可达21cm?(4)先写出y与t的关系式,
再计算长到100cm需几天?初生牛犊不怕虎 小明在电信局办理了某种电话话费套餐,该套餐要求按分钟计费且无论通话多长时间都需要交纳一定的费用作为月租费,办理后某月手机话费y元和通话时间x的关系图如下:观察图象形状,有何特点,你知道该电话套餐的内容吗? ⑴该话费套餐的月租费是多少元?⑵每分钟通话需多少元?100分钟后每分钟通话: 100分钟前每分钟通话: 思考:1011121314课本36页第10题图中的折线表示一骑车人离家的距离Y与时间X的关系,骑车人9点离开家,15点回家,请你根据这个折线表示他的行程过程.(1)12:30分到13:30分离家最远,
这时他离家45千米。·(2)10:30他开始第一次休息,
休息了30分钟,
这时他离家30千米。(3)11:00到12:30他骑了15千米。(4)他在9:00到10:30的平均速度是20千米/时。(4)他在9:00到10:30的平均速度是20千米/时;
他在10:30到12:30的平均速度是7.5千米/时。(5)他返家时的平均速度是30千米/时。(6)14:00时他离家18千米;··
9:30和 时他距家10千米(6)14:00时他离家18千米;1015、某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(1)服药后______时,血液中含药量最高,
达到每毫升_______毫克,接着逐步衰弱。
(2)服药5时,血液中含药量为每毫升____毫克。
(3)当x≤2时y与x之间的函数关系式是_____。
(4)当x≥2时y与x之间的函数关系式是____。
(5)如果每毫升血液中含药量3毫克或3毫克以上
时,治疗疾病最有效,那么这个有效时间范围是___时。.(1)服药后______时,血液中含药量最高,
达到每毫升_______毫克,接着逐步衰弱。
(2)服药10时,血液中含药量为每毫升____毫克。
(3)当x≤2时y与x之间的函数关系式是___________
(4)当x≥2时y与x之间的函数关系式是___________
(5)如果每毫升血液中含药量3毫克或3毫克以上
时,治疗疾病最有效,那么这个有效时间范围是___时。
2603y=3x (x≤2)y=-x+8 (x≥2)5例1: 根据图象,求出相应的函数解析式:3 已知函数(1)当x=0时, y =(2 )当x=2时, y=
(3)当y=0时, x=
(4)当y>0时, x的取值范围 是(6)当-3≤y≤0时, x的取值范围 是(5)当y<1 时, x的取值范围是-311.5X>1.5x<20 ≤ x ≤ 1.51.5例5、已知一次函数图象是线段
1、自变量x的取值范围是
2、函数值y的取值范围是
3、图象与x轴交点为
图象与y轴交点为0≤x ≤6-1≤y ≤2( 4,0 )(0,2)4 、它的解析式为y = - 0.5x + 26、画出函数y=2x+1的图象,并利用图象求出下列题目1、当y≤3时,x的取值范围是多少?答:x≤12、当-3≤y<3时,x的取值范围是多少?答: -2≤x<1
练习 1. 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
(4)函数的图象过原点。
2.将直线y=3x-2向下平移6个单位,得到直线_____________________;
将直线y=-5x-5向上平移4个单位,得到直线_____________________.y=3x-8y=-5x-1一次函数y=b – 3x,y随x的增大而一次函数y= – 2x+b图象过(1, – 2),则b=一次函数y= –x+4的图象经过 象限直线y=kx+b经过一、二、三象限,那么y=bx –k经过 象限函数y=(m –2)x中,已知x1>x2时,y1
A.S是变量 B.t是变量 C.v是变量 D.S是常量3.如图,足球由正五边形皮块(黑色)和正六边形皮块(白色)缝成,试用正六边形的块数x表示正五边形的块数y,并指出其中的变量和常量.(提示:每一个白色皮块周围连着三个黑色皮块)求直线y=2x-1与两坐标轴所围成的三角形面积y=2x-1 -1?解:(如图)∵当x=0时,y=-1 ∴ y=2x-1与y轴的交点为(0,-1) ∵当y=0时,x=?∴ y=2x-1与x轴的交点为(?,0)
= 1/4 ∴AO=? ,BO=1∴SΔAB0= ?·AO·BO = ?×?×1答:直线y=2x-1与两坐标轴所围成的三角形面积为1/4。 B A直线y=kx+3与两坐标轴所围成的三角形面积为9,求k的值y=kx+3 -3/k3解:(如图)∵当x=0时,y=3 ∴ y=kx+3与y轴的交点为(0,3) ∵当y=0时,x=-3/k∴ y=kx+3与x轴的交点为(-3/k,0)
∴ k=-1/2或k=1/2∴SΔAB0= ?·AO·BO=9 ?×3×|-3/k|=9答:k的值为-1/2或1/2 。 B A∴AO=3 ,BO=|-3/k|3.点P(x,y)在第一象限,且x+y=10,点A的坐标为
(8,0),设△OPA的面积为S。
(1)用含x的解析式表示S,写出x的取值范围,画出函数S的图象。·A·8PB(2)当S=12 时点P的坐标402、已知两条直线y1=2x-3和y2=5-x.
(1)在同一坐标系内作出它们的图象;
(2)求出它们的交点A的坐标;
(3)求出这两条直线与x轴围成的三角形ABC的面积. (2)因为A点同时在两条直线上,所以A点坐标同时满足这两个函数的解析式,即A点坐标就是方程组 点,则C(5,0). 老师给出一个函数,甲、乙、丙、丁各指出这个函数的一个性质:
甲:函数不经过第三象限
乙:函数经过第一象限
丙:当X<2时,Y>0
丁:当X <2时,Y随X的增大而减小
请根据以上信息构造一个函数想一想,议一议课堂小结:
1. 你对一次函数的知识都 熟悉了吗?
2. 通过今天的复习,现在会用一次函数的知识解决问题了吧!
3. 希望同学们对今 天复习的知识要十分熟练再见 1. 小星以2米/秒的速度起跑后,先匀速跑5秒,然后突然把速度提高4米/秒,又匀速跑5秒。试写出这段时间里他的跑步路程s(单位:米)随跑步时间x(单位:秒)变化的函数关系式,并画出函数图象。解:依题意得{
s=2x(0≤x≤5) s=10+6(x-5) (5
(2)印刷800份宣传材料,选择哪家印刷厂比较合算?
(3)如果只有3000元用于印刷宣传材料,找哪家印刷厂印制宣传材料能多一些?
探索与思考:已知反比例函数Y=K/2X(K≠0)和一次函数Y=2X-1,其中一次函数的图象经过(a, b),(a+1,b+k)两点。
(1)求反比例函数解析式。
(2)如图已知点A(m,1)在第一象限且同时在上述两个函数图象上求点A的坐标
(3)利用(2)的结果,请回答:
在X轴上是否存在点P使
△AOP为等腰三角形?若存在,
把符合条件的P点坐标都求出来,
若不存在,请说明理由。
