17.2 勾股定理的逆定理课时练习题(含答案)
文档属性
| 名称 | 17.2 勾股定理的逆定理课时练习题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 948.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-16 16:48:58 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版八年级数学下册第十七章《17.2勾股定理的逆定理》
课时练习题(含答案)
一、单选题
1.如果用,a、b、c表示的三边,那么分别满足下列条件的三角形中,直角三角形有( )
①b2=c2﹣a2;②a:b:c=3:4:5;③∠C=∠A﹣∠B;④∠A:∠B:∠C=12:13:15
A.1个 B.2个 C.3个 D.4个
2.若,,是一组勾股数,则的值为( )
A. B. C.或 D.
3.在中,的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果,那么是直角三角形
B.如果,那么是直角三角形且
C.如果,那么是直角三角形
D.如果,那么是直角三角形
4.三角形的边长之比为:①1.5:2:2.5;②4:7.5:8.5;③1::2;④3.5:4.5:5.5.其中可以构成直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
5.如图,在四边形中,,,,,且,则四边形的面积是( )
A.4 B. C. D.
6.在中,,,的对边分别是,,,下列命题中的假命题是( )
A.如果,则是直角三角形,且
B.如果,则是直角三角形,且
C.如果,则是直角三角形,且
D.如果:,则是直角三角形,且
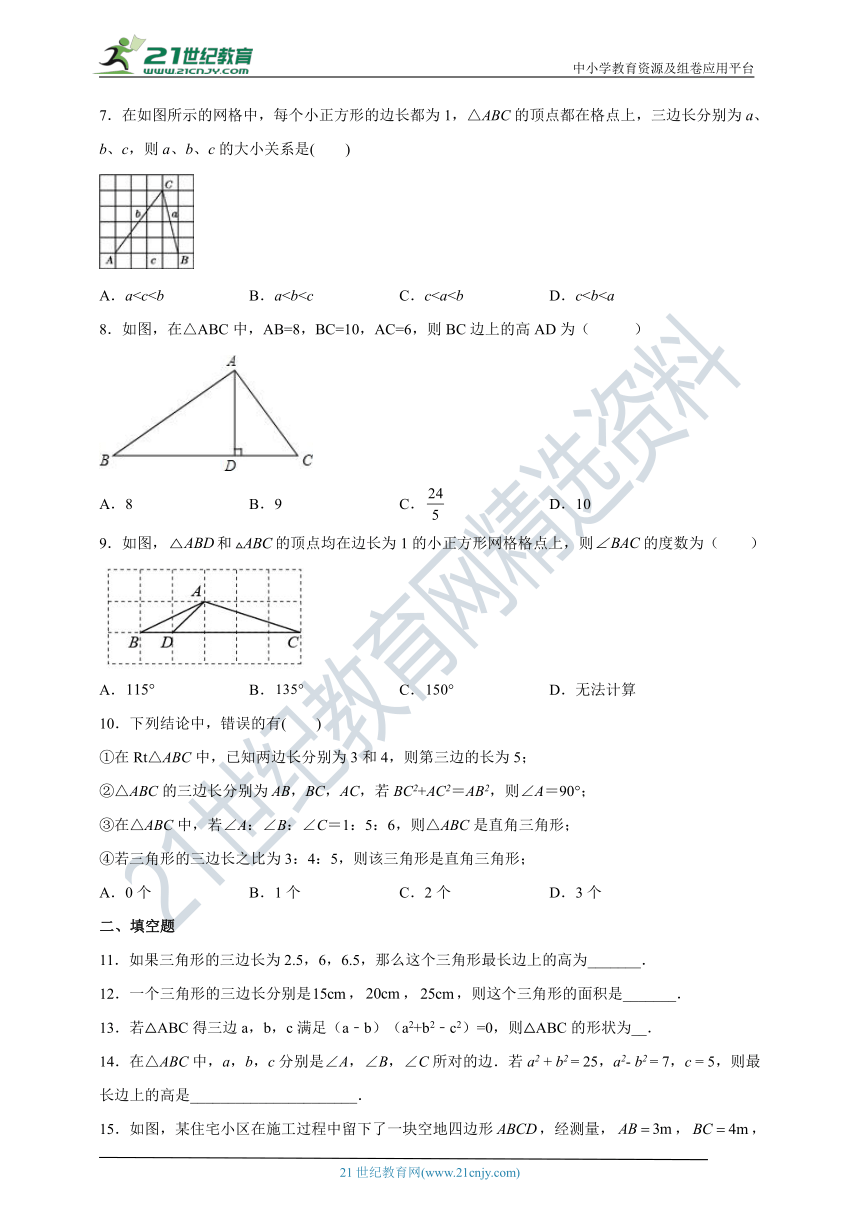
7.在如图所示的网格中,每个小正方形的边长都为1,△ABC的顶点都在格点上,三边长分别为a、b、c,则a、b、c的大小关系是( )
A.a8.如图,在△ABC中,AB=8,BC=10,AC=6,则BC边上的高AD为( )
A.8 B.9 C. D.10
9.如图,和的顶点均在边长为1的小正方形网格格点上,则的度数为( )
A. B. C. D.无法计算
10.下列结论中,错误的有( )
①在Rt△ABC中,已知两边长分别为3和4,则第三边的长为5;
②△ABC的三边长分别为AB,BC,AC,若BC2+AC2=AB2,则∠A=90°;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④若三角形的三边长之比为3:4:5,则该三角形是直角三角形;
A.0个 B.1个 C.2个 D.3个
二、填空题
11.如果三角形的三边长为2.5,6,6.5,那么这个三角形最长边上的高为_______.
12.一个三角形的三边长分别是,,,则这个三角形的面积是_______.
13.若△ABC得三边a,b,c满足(a﹣b)(a2+b2﹣c2)=0,则△ABC的形状为__.
14.在△ABC中,a,b,c分别是∠A,∠B,∠C所对的边.若a2 + b2 = 25,a2- b2 = 7,c = 5,则最长边上的高是______________________.
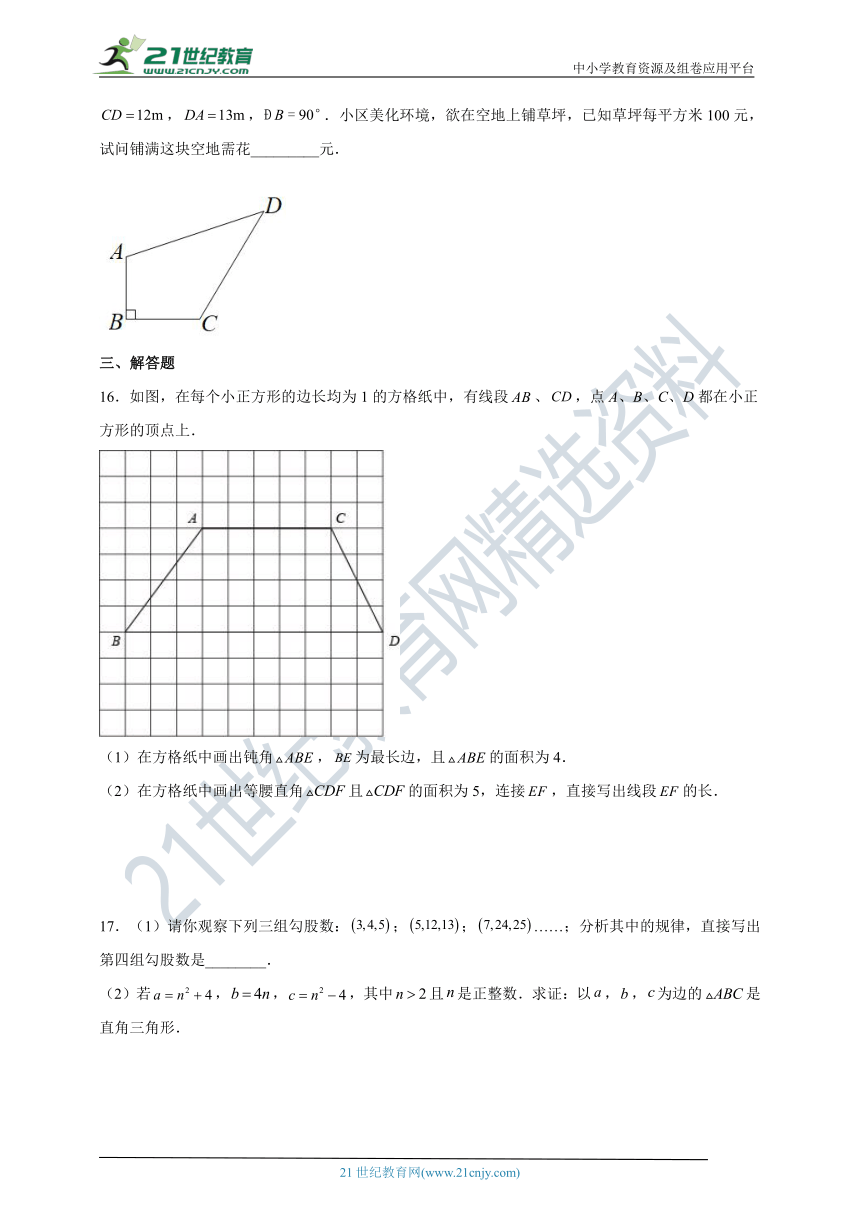
15.如图,某住宅小区在施工过程中留下了一块空地四边形,经测量,,,,,.小区美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地需花_________元.
三、解答题
16.如图,在每个小正方形的边长均为1的方格纸中,有线段、,点A、B、C、D都在小正方形的顶点上.
(1)在方格纸中画出钝角,为最长边,且的面积为4.
(2)在方格纸中画出等腰直角且的面积为5,连接,直接写出线段的长.
17.(1)请你观察下列三组勾股数:;;……;分析其中的规律,直接写出第四组勾股数是________.
(2)若,,,其中且是正整数.求证:以,,为边的是直角三角形.
18.定义:如图,点M、N把线段AB分割成AM、MN、NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.
(1)已知M、N把线段AB分割成AM、MN、NB,若AM=2,MN=4,,则点M、N是线段AB的勾股分割点吗?请说明理由.
(2)已知点M、N是线段AB的勾股分割点,且AM为直角边,若AB=12,,求BN的长.
19.我们规定,三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差.如图1,在中,是边上的中线,与的“广益值”就等于的值,可记为
(1)在中,若,,求的值.
(2)如图2,在中,,,求,的值.
(3)如图3,在中,是边上的中线,,,,求和的长.
参考答案
1.C2.B3.B4.C5.C6.B7.C8.C9.B10.C
11.
12.
13.等腰三角形或直角三角形或等腰直角三角形
14.
15.3600
16.(1)如下图,为钝角三角形,且为最长边
∵每个小正方形的边长均为1的方格纸
∴,的边对应的高为4
∴
∴图中钝角即为所求;
(2)如下图,
根据题意,得:
∴,
∴为等腰直角三角形
∴
连接
∴.
17.解:(1)∵①3=2×1+1,4=2×12+2×1,5=2×12+2×1+1;
②5=2×2+1,12=2×22+2×2,13=2×22+2×2+1;
③7=2×3+1,24=2×32+2×3,25=2×32+2×3+1;
∴第四组勾股数是:
9=2×4+1,40=2×42+2×4,41=2×42+2×4+1;
即9,40,41;
(2)∵,,,
∴,
,
,
满足,
∴以,,为边的是直角三角形.
18.(1)点M、N是线段AB的勾股分割点,理由如下,
,,
,
AM、MN、NB为边的三角形是一个直角三角形,
点M、N是线段AB的勾股分割点.
(2)
设BN=x,则MN=12-AM-BN=7-x,
①当MN为最大线段时,依题意;
即,
解得,
②当BN为最大线段时,依题意,
即,
解得.
综上所述,的长为或.
19.解:(1)已知如图:AO为BC上的中线,
在Rt中,
AO2-OC2=AC2
因为
所以AO2-OC2=81
所以AC2=81
所以AC=9.
(2)①如图2,取BC的中点D,连接AO,
∵AB=AC,
∴AO⊥BC,
在△ABC中,AB=AC,∠BAC=120°,
∴∠ABC=30°,
在Rt△AOB中,AB=12,∠ABC=30°,
∴AO=6,OB==,
∴ABAC=AO2﹣BO2=36﹣108=﹣72,
②取AC的中点D,连接BD,
∴AD=CD=AC=6,过点B作BE⊥AC交CA的延长线于E,
在Rt△ABE中,∠BAE=180°﹣∠BAC=60°,
∴∠ABE=30°,
∵AB=12,
∴AE=6,BE=,
∴DE=AD+AE=12,
在Rt△BED中,根据勾股定理得,BD=
∴BABC=BD2﹣CD2=216;
(3)作BD⊥CD,
因为,,
所以BD=2,
因为,是边上的中线,
所以AO2-OC2=-64,
所以OC2-AO2=64,
因为AC2=82=64,
所以OC2-AO2= AC2
所以∠OAC=90°
所以OA=
所以OC=
所以BC=2OC=2,
在Rt△BCD中,
CD=
所以AD=CD-AC=16-8=8
所以AB=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级数学下册第十七章《17.2勾股定理的逆定理》
课时练习题(含答案)
一、单选题
1.如果用,a、b、c表示的三边,那么分别满足下列条件的三角形中,直角三角形有( )
①b2=c2﹣a2;②a:b:c=3:4:5;③∠C=∠A﹣∠B;④∠A:∠B:∠C=12:13:15
A.1个 B.2个 C.3个 D.4个
2.若,,是一组勾股数,则的值为( )
A. B. C.或 D.
3.在中,的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果,那么是直角三角形
B.如果,那么是直角三角形且
C.如果,那么是直角三角形
D.如果,那么是直角三角形
4.三角形的边长之比为:①1.5:2:2.5;②4:7.5:8.5;③1::2;④3.5:4.5:5.5.其中可以构成直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
5.如图,在四边形中,,,,,且,则四边形的面积是( )
A.4 B. C. D.
6.在中,,,的对边分别是,,,下列命题中的假命题是( )
A.如果,则是直角三角形,且
B.如果,则是直角三角形,且
C.如果,则是直角三角形,且
D.如果:,则是直角三角形,且
7.在如图所示的网格中,每个小正方形的边长都为1,△ABC的顶点都在格点上,三边长分别为a、b、c,则a、b、c的大小关系是( )
A.a
A.8 B.9 C. D.10
9.如图,和的顶点均在边长为1的小正方形网格格点上,则的度数为( )
A. B. C. D.无法计算
10.下列结论中,错误的有( )
①在Rt△ABC中,已知两边长分别为3和4,则第三边的长为5;
②△ABC的三边长分别为AB,BC,AC,若BC2+AC2=AB2,则∠A=90°;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④若三角形的三边长之比为3:4:5,则该三角形是直角三角形;
A.0个 B.1个 C.2个 D.3个
二、填空题
11.如果三角形的三边长为2.5,6,6.5,那么这个三角形最长边上的高为_______.
12.一个三角形的三边长分别是,,,则这个三角形的面积是_______.
13.若△ABC得三边a,b,c满足(a﹣b)(a2+b2﹣c2)=0,则△ABC的形状为__.
14.在△ABC中,a,b,c分别是∠A,∠B,∠C所对的边.若a2 + b2 = 25,a2- b2 = 7,c = 5,则最长边上的高是______________________.
15.如图,某住宅小区在施工过程中留下了一块空地四边形,经测量,,,,,.小区美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地需花_________元.
三、解答题
16.如图,在每个小正方形的边长均为1的方格纸中,有线段、,点A、B、C、D都在小正方形的顶点上.
(1)在方格纸中画出钝角,为最长边,且的面积为4.
(2)在方格纸中画出等腰直角且的面积为5,连接,直接写出线段的长.
17.(1)请你观察下列三组勾股数:;;……;分析其中的规律,直接写出第四组勾股数是________.
(2)若,,,其中且是正整数.求证:以,,为边的是直角三角形.
18.定义:如图,点M、N把线段AB分割成AM、MN、NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.
(1)已知M、N把线段AB分割成AM、MN、NB,若AM=2,MN=4,,则点M、N是线段AB的勾股分割点吗?请说明理由.
(2)已知点M、N是线段AB的勾股分割点,且AM为直角边,若AB=12,,求BN的长.
19.我们规定,三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差.如图1,在中,是边上的中线,与的“广益值”就等于的值,可记为
(1)在中,若,,求的值.
(2)如图2,在中,,,求,的值.
(3)如图3,在中,是边上的中线,,,,求和的长.
参考答案
1.C2.B3.B4.C5.C6.B7.C8.C9.B10.C
11.
12.
13.等腰三角形或直角三角形或等腰直角三角形
14.
15.3600
16.(1)如下图,为钝角三角形,且为最长边
∵每个小正方形的边长均为1的方格纸
∴,的边对应的高为4
∴
∴图中钝角即为所求;
(2)如下图,
根据题意,得:
∴,
∴为等腰直角三角形
∴
连接
∴.
17.解:(1)∵①3=2×1+1,4=2×12+2×1,5=2×12+2×1+1;
②5=2×2+1,12=2×22+2×2,13=2×22+2×2+1;
③7=2×3+1,24=2×32+2×3,25=2×32+2×3+1;
∴第四组勾股数是:
9=2×4+1,40=2×42+2×4,41=2×42+2×4+1;
即9,40,41;
(2)∵,,,
∴,
,
,
满足,
∴以,,为边的是直角三角形.
18.(1)点M、N是线段AB的勾股分割点,理由如下,
,,
,
AM、MN、NB为边的三角形是一个直角三角形,
点M、N是线段AB的勾股分割点.
(2)
设BN=x,则MN=12-AM-BN=7-x,
①当MN为最大线段时,依题意;
即,
解得,
②当BN为最大线段时,依题意,
即,
解得.
综上所述,的长为或.
19.解:(1)已知如图:AO为BC上的中线,
在Rt中,
AO2-OC2=AC2
因为
所以AO2-OC2=81
所以AC2=81
所以AC=9.
(2)①如图2,取BC的中点D,连接AO,
∵AB=AC,
∴AO⊥BC,
在△ABC中,AB=AC,∠BAC=120°,
∴∠ABC=30°,
在Rt△AOB中,AB=12,∠ABC=30°,
∴AO=6,OB==,
∴ABAC=AO2﹣BO2=36﹣108=﹣72,
②取AC的中点D,连接BD,
∴AD=CD=AC=6,过点B作BE⊥AC交CA的延长线于E,
在Rt△ABE中,∠BAE=180°﹣∠BAC=60°,
∴∠ABE=30°,
∵AB=12,
∴AE=6,BE=,
∴DE=AD+AE=12,
在Rt△BED中,根据勾股定理得,BD=
∴BABC=BD2﹣CD2=216;
(3)作BD⊥CD,
因为,,
所以BD=2,
因为,是边上的中线,
所以AO2-OC2=-64,
所以OC2-AO2=64,
因为AC2=82=64,
所以OC2-AO2= AC2
所以∠OAC=90°
所以OA=
所以OC=
所以BC=2OC=2,
在Rt△BCD中,
CD=
所以AD=CD-AC=16-8=8
所以AB=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
