18.3 一次函数[下学期]
图片预览




文档简介
课件11张PPT。函数复习课B(0,b)xyo4
3
2
1-1
-2
-3
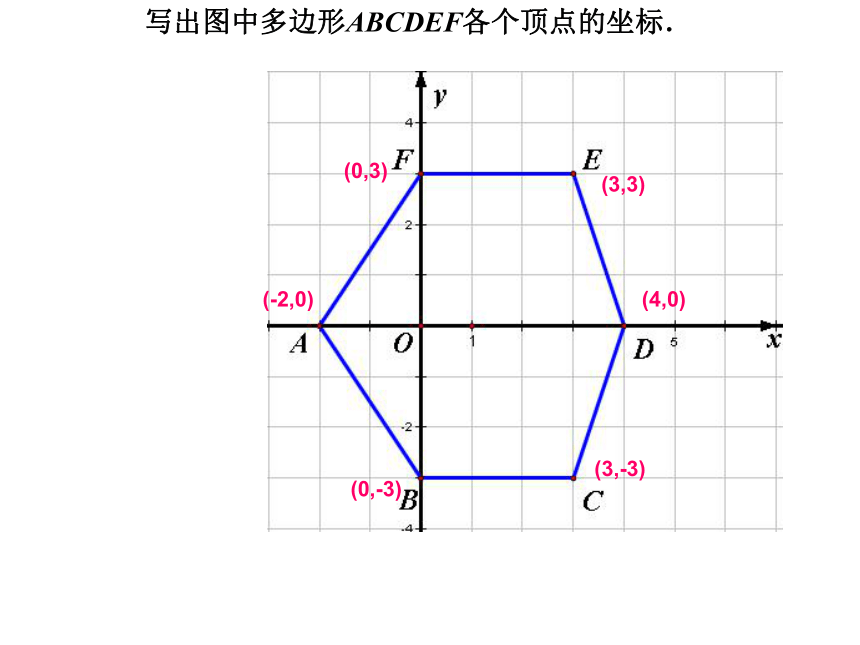
-41 2 3 4 -4 -3 -2 -1..A(a,0) 写出图中多边形ABCDEF各个顶点的坐标.(-2,0)(0,-3)(3,-3)(4,0)(3,3)(0,3)(1)关于x轴对称的两点:横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的两点:纵坐标相同,横坐标互为相反数;
(3)关于原点对称的两点:横坐标互为相反数,纵坐标也互为相反数. 正比例函数y=kx的图象是一条过原点的直线;
正比例函数y=kx的图象也称为直线y=kx. 两个一次函数(即两条直线),当k值相等,b值不等时,两条直线互相平行. 直线y=kx+b向上平移a个单位得到直线y=kx+(b+a);
直线y=kx+b向下平移a个单位得到直线y=kx+(b-a).一次函数y=kx+b的图象是一条过(0,b)的直线;一次函数y=kx+b的性质 当k>0时,y随x的增大而增大,函数图象从左到右上升; 当k<0时,y随x的而增大减小,函数图象从左到右下降; 当b>0时,直线交y轴上半轴 当b<0时,直线交y轴下半轴拓展与应用一次函数y=kx+b中,b>0,且y随x的增大而
减小,则它的图象大致为( )EX:根据下列条件,求下列函数的解析式.(1)正比例函数中,当x=2.5时,y=10.解:设该正比例函数的解析式为y=kx.把x=2.5,y=10代入上式,可得10=2.5k.所以k=4,即函数解析式为:y=4x.(2)一次函数y=-2x+b中,当x=2时,y=-1.解:把x=2,y=-1代入 y=-2x+b,可得:
-1=-4+b所以b=3,即一次函数为y=-2x+3.待定系数法巩固提高:1.当a=______时,函数y=(a+2)x2a-3-5x+6是一次函数.
则该一次函数的解析式为_____________2.已知一次函数中,当x=2时,y=1;当x=-1时,y=-2.
则该一次函数的解析式为_____________3.已知函数y=(m+5)x-b+2,当_____时,此函数是一次
函数;当_______时,此函数是正比例函数.反比例函数的性质1.当k>0时,函数的图象在 、 象限,在每一个象限内,y随x的增大而 ;
2.当k<0时,函数的图象分别在第二、四象限内,在每一个象限内,y随x的增大而增大。
一三减小K<0K<0K>0K>0y随着x
增大而
增大y随着x
增大而
减小在每一象限
内, y随着
x增大而增大在每一象限
内,y随着
x增大而减小 y=kx(k≠0)
正比例函数和反比例函数的区别
3
2
1-1
-2
-3
-41 2 3 4 -4 -3 -2 -1..A(a,0) 写出图中多边形ABCDEF各个顶点的坐标.(-2,0)(0,-3)(3,-3)(4,0)(3,3)(0,3)(1)关于x轴对称的两点:横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的两点:纵坐标相同,横坐标互为相反数;
(3)关于原点对称的两点:横坐标互为相反数,纵坐标也互为相反数. 正比例函数y=kx的图象是一条过原点的直线;
正比例函数y=kx的图象也称为直线y=kx. 两个一次函数(即两条直线),当k值相等,b值不等时,两条直线互相平行. 直线y=kx+b向上平移a个单位得到直线y=kx+(b+a);
直线y=kx+b向下平移a个单位得到直线y=kx+(b-a).一次函数y=kx+b的图象是一条过(0,b)的直线;一次函数y=kx+b的性质 当k>0时,y随x的增大而增大,函数图象从左到右上升; 当k<0时,y随x的而增大减小,函数图象从左到右下降; 当b>0时,直线交y轴上半轴 当b<0时,直线交y轴下半轴拓展与应用一次函数y=kx+b中,b>0,且y随x的增大而
减小,则它的图象大致为( )EX:根据下列条件,求下列函数的解析式.(1)正比例函数中,当x=2.5时,y=10.解:设该正比例函数的解析式为y=kx.把x=2.5,y=10代入上式,可得10=2.5k.所以k=4,即函数解析式为:y=4x.(2)一次函数y=-2x+b中,当x=2时,y=-1.解:把x=2,y=-1代入 y=-2x+b,可得:
-1=-4+b所以b=3,即一次函数为y=-2x+3.待定系数法巩固提高:1.当a=______时,函数y=(a+2)x2a-3-5x+6是一次函数.
则该一次函数的解析式为_____________2.已知一次函数中,当x=2时,y=1;当x=-1时,y=-2.
则该一次函数的解析式为_____________3.已知函数y=(m+5)x-b+2,当_____时,此函数是一次
函数;当_______时,此函数是正比例函数.反比例函数的性质1.当k>0时,函数的图象在 、 象限,在每一个象限内,y随x的增大而 ;
2.当k<0时,函数的图象分别在第二、四象限内,在每一个象限内,y随x的增大而增大。
一三减小K<0K<0K>0K>0y随着x
增大而
增大y随着x
增大而
减小在每一象限
内, y随着
x增大而增大在每一象限
内,y随着
x增大而减小 y=kx(k≠0)
正比例函数和反比例函数的区别
