6.3.2二项式系数的性质 课件(共20张PPT)
文档属性
| 名称 | 6.3.2二项式系数的性质 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 512.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-15 01:00:00 | ||
图片预览



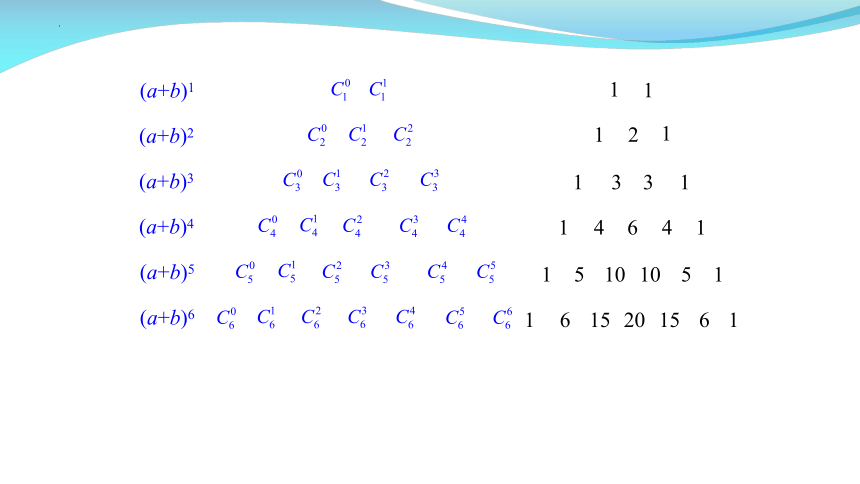





文档简介
(共20张PPT)
6.3.2 二项式系数的性质
1.了解二项式系数的性质并能简单应用.
2.掌握“赋值法”并会灵活应用.
你从上面的表示形式可以直观地看出什么规律?
通过前面的学习,我们知道:(a+b)n的展开式的二项式系数,当 n 取正整数时可以表示成如下形式:
(a+b)1 1 1
(a+b)2 1 2 1
(a+b)3 1 3 3 1
(a+b)4 1 4 6 4 1
(a+b)5 1 5 10 10 5 1
(a+b)6 1 6 15 20 15 6 1
1
6
15
20
15
6
1
(a+b)1
(a+b)3
(a+b)4
(a+b)5
(a+b)2
(a+b)6
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
二项式系数的性质
1.对称性:与首末两端“等距离”的两个二项式系数相等.
实际上,由 ,
所以
2.增减性与最大值
二项式系数先增后减,
当 n 为偶数时,中间的一项 取得最大值;
当 n 为奇数时,中间的两项 与 相等,且同时取得最大值.
3.各二项式系数的和
已知
令 ,得
这就是说, 的展开式的各二项式系数的和等于 .
二项式系数性质的应用
例1.(1)已知 的展开式中只有第5项的二项式系数最大,则n=( )
A.11 B.10 C.9 D.8
(2)在 的二项展开式中与第3项二项式系数相同的项是( )
A.第8项 B.第7项 C.第9项 D.第10项
C
D
1.二项式系数最大的项的求法
求二项式系数最大的项,根据二项式系数的性质对 中的 n 进行讨论:
(1)当 n 为偶数时,中间一项的二项式系数最大;
(2)当 n 为奇数时,中间两项的二项式系数最大.
2.展开式中系数最大的项的求法
求展开式中系数最大的项与求二项式系数最大的项是不同的,需要根据各项系数的正、负变化情况进行分析.
如求 (a,b∈R)的展开式中系数最大的项,一般采用待定系数法.设展开式中各项系数分别为A0,A1,A2,…,An,且第 项最大,
应用 解出 k,即得出系数最大的项.
1.(1)在 的二项展开式中,若只有x5的系数最大,则 n 等于( )
A.8 B.9 C.10 D.11
(2)已知 的展开式中第6项与第7项的系数相等,求展开式中系数最大的项.
C
求二项展开的系数和
例2.若 ,求
(1) ;
(2) ;
(3) ;
(4) .
二项展开式中系数和的求法
(1)对形如 , 的式子求其展开式的各项系数之和,常用赋值法,只需令 即可;对 的式子求其展开式各项系数之和,只需令 即可;
(2)一般地,若 ,则 f(x)展开式中:
各项系数之和为 f(1);
奇数项系数之和为 ;
偶数项系数之和为 .
(3)赋值法是解决二项展开式中项的系数常用的方法,根据题目要求,灵活赋给字母不同的值.一般地,要使展开式中项的关系变为系数的关系.
令 可得常数项;
令 可得所有项系数之和;
令 可得偶次项系数之和与奇次项系数之和的差.
2.设 .
(1)求 的值;
(2)求 的值;
(3)求 的值.
解:(1)令 ,得 ,
令 ,得 ,
所以
(2)由(1) ①
令 ,得 ②
①-②得 ,
所以 .
(3)因为 ,
所以 k 为奇数时, ,k 为偶数时, ,
故 .
整除、求余数问题
例3.(1)用二项式定理证明 能被100整除;
(2)求 除以7的余数.
解:(1)因为
所以 能被100整除.
(2)因为
所以 被7除余数为4.
整除性问题或求余数问题的处理方法
(1)解决这类问题,必须构造一个与题目条件有关的二项式;
(2)用二项式定理处理这类问题,通常把被除数的底数写成除数(或与除数密切关联的数)与某数的和或差的形式,再用二项式定理展开,只考虑后面(或者是前面)的几项就可以了.
3.求 除以9的余数.
解:因为
显然上式括号内的数是正整数,故 除以9的余数为7.
6.3.2 二项式系数的性质
1.了解二项式系数的性质并能简单应用.
2.掌握“赋值法”并会灵活应用.
你从上面的表示形式可以直观地看出什么规律?
通过前面的学习,我们知道:(a+b)n的展开式的二项式系数,当 n 取正整数时可以表示成如下形式:
(a+b)1 1 1
(a+b)2 1 2 1
(a+b)3 1 3 3 1
(a+b)4 1 4 6 4 1
(a+b)5 1 5 10 10 5 1
(a+b)6 1 6 15 20 15 6 1
1
6
15
20
15
6
1
(a+b)1
(a+b)3
(a+b)4
(a+b)5
(a+b)2
(a+b)6
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
二项式系数的性质
1.对称性:与首末两端“等距离”的两个二项式系数相等.
实际上,由 ,
所以
2.增减性与最大值
二项式系数先增后减,
当 n 为偶数时,中间的一项 取得最大值;
当 n 为奇数时,中间的两项 与 相等,且同时取得最大值.
3.各二项式系数的和
已知
令 ,得
这就是说, 的展开式的各二项式系数的和等于 .
二项式系数性质的应用
例1.(1)已知 的展开式中只有第5项的二项式系数最大,则n=( )
A.11 B.10 C.9 D.8
(2)在 的二项展开式中与第3项二项式系数相同的项是( )
A.第8项 B.第7项 C.第9项 D.第10项
C
D
1.二项式系数最大的项的求法
求二项式系数最大的项,根据二项式系数的性质对 中的 n 进行讨论:
(1)当 n 为偶数时,中间一项的二项式系数最大;
(2)当 n 为奇数时,中间两项的二项式系数最大.
2.展开式中系数最大的项的求法
求展开式中系数最大的项与求二项式系数最大的项是不同的,需要根据各项系数的正、负变化情况进行分析.
如求 (a,b∈R)的展开式中系数最大的项,一般采用待定系数法.设展开式中各项系数分别为A0,A1,A2,…,An,且第 项最大,
应用 解出 k,即得出系数最大的项.
1.(1)在 的二项展开式中,若只有x5的系数最大,则 n 等于( )
A.8 B.9 C.10 D.11
(2)已知 的展开式中第6项与第7项的系数相等,求展开式中系数最大的项.
C
求二项展开的系数和
例2.若 ,求
(1) ;
(2) ;
(3) ;
(4) .
二项展开式中系数和的求法
(1)对形如 , 的式子求其展开式的各项系数之和,常用赋值法,只需令 即可;对 的式子求其展开式各项系数之和,只需令 即可;
(2)一般地,若 ,则 f(x)展开式中:
各项系数之和为 f(1);
奇数项系数之和为 ;
偶数项系数之和为 .
(3)赋值法是解决二项展开式中项的系数常用的方法,根据题目要求,灵活赋给字母不同的值.一般地,要使展开式中项的关系变为系数的关系.
令 可得常数项;
令 可得所有项系数之和;
令 可得偶次项系数之和与奇次项系数之和的差.
2.设 .
(1)求 的值;
(2)求 的值;
(3)求 的值.
解:(1)令 ,得 ,
令 ,得 ,
所以
(2)由(1) ①
令 ,得 ②
①-②得 ,
所以 .
(3)因为 ,
所以 k 为奇数时, ,k 为偶数时, ,
故 .
整除、求余数问题
例3.(1)用二项式定理证明 能被100整除;
(2)求 除以7的余数.
解:(1)因为
所以 能被100整除.
(2)因为
所以 被7除余数为4.
整除性问题或求余数问题的处理方法
(1)解决这类问题,必须构造一个与题目条件有关的二项式;
(2)用二项式定理处理这类问题,通常把被除数的底数写成除数(或与除数密切关联的数)与某数的和或差的形式,再用二项式定理展开,只考虑后面(或者是前面)的几项就可以了.
3.求 除以9的余数.
解:因为
显然上式括号内的数是正整数,故 除以9的余数为7.
