18.3 一次函数的应用[下学期]
图片预览
文档简介
一次函数的应用
一、教学目标:
1、 知识目标是学生了解函数是日常生活和生产实际中应用十分广泛的数学模型,使学生掌握把实际问题归结为函数问题来解决的思想方法。
2、 能力目标是提高学生应用函数、方程、不等式知识解决实际问题的能力。
3、 情感目标是使学生接受数形结合、分类讨论的数学思想,使学生进一步体验客观事物是互相联系又互相制约的,而且是有规律地运动、变化着的辨证唯物主义观点。
二、教学重点、难点:观察和应用一次函数,获取信息,解决问题。
三、教学过程:
教学步骤 教师活动 学生活动 设计思想
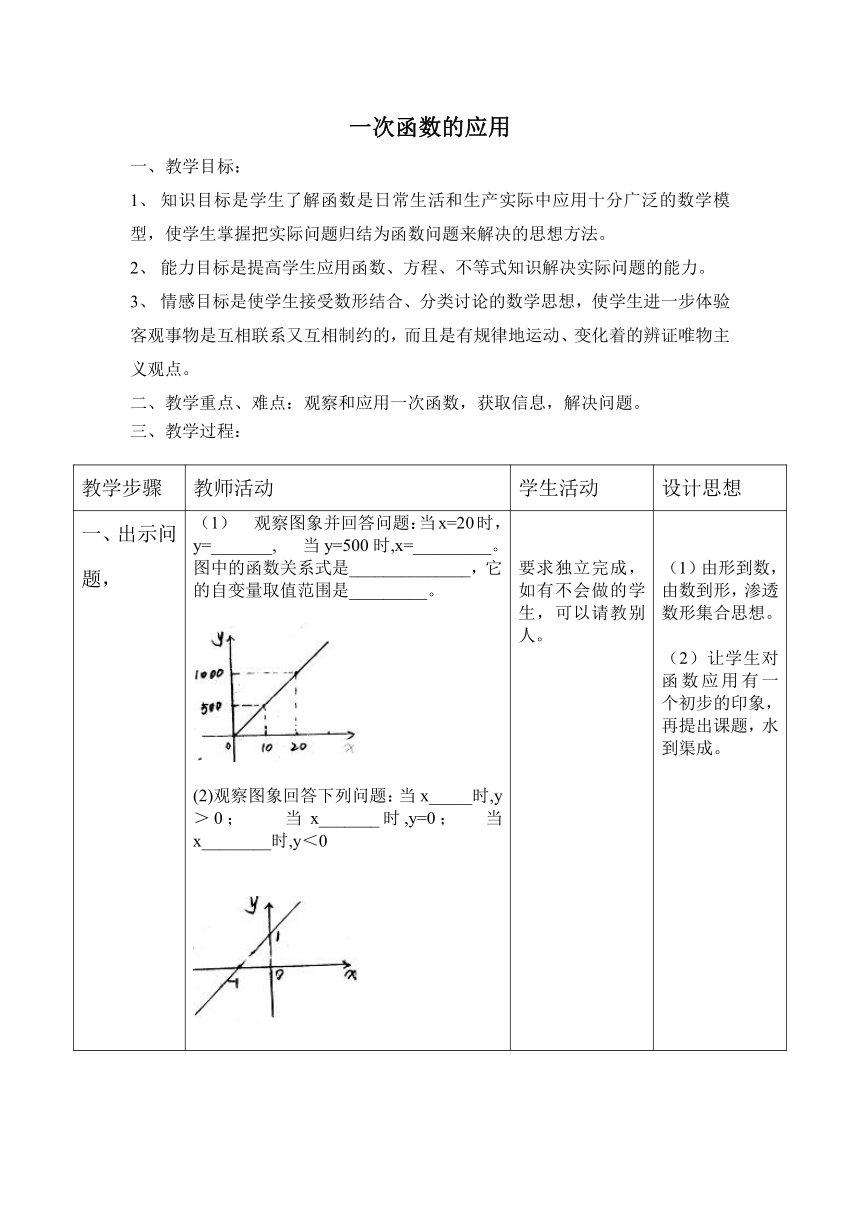
一、出示问题, (1) 观察图象并回答问题:当x=20时,y=_______, 当y=500时,x=_________。图中的函数关系式是______________,它的自变量取值范围是_________。(2)观察图象回答下列问题:当x_____时,y>0; 当x_______时,y=0; 当x________时,y<0 要求独立完成,如有不会做的学生,可以请教别人。 (1)由形到数,由数到形,渗透数形集合思想。(2)让学生对函数应用有一个初步的印象,再提出课题,水到渠成。
教学步骤 教师活动 学生活动 设计思想
师生互动,复习生活中的一次函数。(热点问题) (1)从去年11月份开始,“禽流感”继“非典”之后又一次引起人们的恐慌。1、在抗击“禽流感”中,某医药研究所开发了一种预防“禽流感”的药品.经试验这种药品的效果得到:每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示.当成人按规定剂量服药后: (1)服药后______时,血液中含药量最高, 达到每毫升_______微克,接着逐步衰减。(2)服药8时,血液中含药量为每毫升____微克。(3)当x≤1时y与x之间的函数关系式是_____。(4)当x≥1时y与x之间的函数关系式是____。(5)如果每毫升血液中含药量为2微克或2微克以上时,对预防“禽流感”是有效的,那么这个有效时间是________小时。 学生经过图象观察,得到血液中的含量与时间的关系。讨论x≥1和x≤1时,y与x之间函数关系式。3、学之间可以互相帮助。 1、仔细观察图形得到数据。2、通过得到的数据,师生互动,合作学习,同时在解题中渗透数形集合和分类的数学思想
(环保型问题) 2、长兴县为了加强公民的节水意识,合理利用水资源,制定了如下的收费标准:每户每月用水量不超过6米3时,水费按0.6元/米3收费,每户每月用水量超过6米3时,超过的部分按1元/米3。设每户每月用水量为x米3,应缴纳y元。(1)写出y与x之间的函数关系式,并判断它们是否为一次函数。(2) 已知某户5月份的用水量为7.2米3 求该用户5月份的水费。 学生分类讨论在不同的自变量下,有不同的函数关系式。 1、分类思想和转化思想。2、加强学生的环保意识。
(决策型问题) 一家工厂生产彩电,每件产品的出厂价为1万元,其原材料成本价(含设备损耗等)为0.55万元,同时在生产过程中平均每生产一件产品有1千克的废渣产生.为达到国家环保要求,需要对废渣进行处理.现有两种方案可供选择.方案一:由工厂对废渣直接进行处理,每处理1千克废渣所用的原料费为0.05万元,并且每月设备维护及损耗费为20万元.方案二:工厂将废渣集中到废渣处理厂统一处理.每处理1千克废渣需付0.1万元的处理费.(1)设工厂每月生产x件产品,每月利润为y万元,分别求出用方案一和方案二处理废渣时,y与x之间的函数关系式(利润=总收入-总支出);(2)假如你是厂长,那么如何根据月生产量选择处理方案,既可达到环保要求又最合算。 各小组中的同学相互讨论,发表自己的看法,找出最佳的方案 1、注意函数和不等式之间的转化,渗透转化思想。2、提高学生用数学解决实际问题的能力。
(学科整合型问题) 声音在空气中传播的速度y(m/s)(简称声速)是气温x(℃)的一次函数.下表列出了一组不同气温时的声速:(1) 求y与x之间的函数关系式;(2) 气温x=22(℃)时,某人看到烟花燃放5s后才听到声响,那么此人与燃放的烟花所在地约相距多远? 请同学们回忆声音在空气中的传播速度和温度之间的关系。用待定系数法求函数解析式。3、能不能找到一种更方便的解题方法。 1、引起兴趣。2、体现直观性原则
四、课堂小结
(1)这节课我们学习了哪些数学思想和解题方法?
(2)经过这节课的学习,你有哪些收获?
五、作业:见课后练习。
一、教学目标:
1、 知识目标是学生了解函数是日常生活和生产实际中应用十分广泛的数学模型,使学生掌握把实际问题归结为函数问题来解决的思想方法。
2、 能力目标是提高学生应用函数、方程、不等式知识解决实际问题的能力。
3、 情感目标是使学生接受数形结合、分类讨论的数学思想,使学生进一步体验客观事物是互相联系又互相制约的,而且是有规律地运动、变化着的辨证唯物主义观点。
二、教学重点、难点:观察和应用一次函数,获取信息,解决问题。
三、教学过程:
教学步骤 教师活动 学生活动 设计思想
一、出示问题, (1) 观察图象并回答问题:当x=20时,y=_______, 当y=500时,x=_________。图中的函数关系式是______________,它的自变量取值范围是_________。(2)观察图象回答下列问题:当x_____时,y>0; 当x_______时,y=0; 当x________时,y<0 要求独立完成,如有不会做的学生,可以请教别人。 (1)由形到数,由数到形,渗透数形集合思想。(2)让学生对函数应用有一个初步的印象,再提出课题,水到渠成。
教学步骤 教师活动 学生活动 设计思想
师生互动,复习生活中的一次函数。(热点问题) (1)从去年11月份开始,“禽流感”继“非典”之后又一次引起人们的恐慌。1、在抗击“禽流感”中,某医药研究所开发了一种预防“禽流感”的药品.经试验这种药品的效果得到:每毫升血液中含药量y(微克)随时间x(小时)的变化如图所示.当成人按规定剂量服药后: (1)服药后______时,血液中含药量最高, 达到每毫升_______微克,接着逐步衰减。(2)服药8时,血液中含药量为每毫升____微克。(3)当x≤1时y与x之间的函数关系式是_____。(4)当x≥1时y与x之间的函数关系式是____。(5)如果每毫升血液中含药量为2微克或2微克以上时,对预防“禽流感”是有效的,那么这个有效时间是________小时。 学生经过图象观察,得到血液中的含量与时间的关系。讨论x≥1和x≤1时,y与x之间函数关系式。3、学之间可以互相帮助。 1、仔细观察图形得到数据。2、通过得到的数据,师生互动,合作学习,同时在解题中渗透数形集合和分类的数学思想
(环保型问题) 2、长兴县为了加强公民的节水意识,合理利用水资源,制定了如下的收费标准:每户每月用水量不超过6米3时,水费按0.6元/米3收费,每户每月用水量超过6米3时,超过的部分按1元/米3。设每户每月用水量为x米3,应缴纳y元。(1)写出y与x之间的函数关系式,并判断它们是否为一次函数。(2) 已知某户5月份的用水量为7.2米3 求该用户5月份的水费。 学生分类讨论在不同的自变量下,有不同的函数关系式。 1、分类思想和转化思想。2、加强学生的环保意识。
(决策型问题) 一家工厂生产彩电,每件产品的出厂价为1万元,其原材料成本价(含设备损耗等)为0.55万元,同时在生产过程中平均每生产一件产品有1千克的废渣产生.为达到国家环保要求,需要对废渣进行处理.现有两种方案可供选择.方案一:由工厂对废渣直接进行处理,每处理1千克废渣所用的原料费为0.05万元,并且每月设备维护及损耗费为20万元.方案二:工厂将废渣集中到废渣处理厂统一处理.每处理1千克废渣需付0.1万元的处理费.(1)设工厂每月生产x件产品,每月利润为y万元,分别求出用方案一和方案二处理废渣时,y与x之间的函数关系式(利润=总收入-总支出);(2)假如你是厂长,那么如何根据月生产量选择处理方案,既可达到环保要求又最合算。 各小组中的同学相互讨论,发表自己的看法,找出最佳的方案 1、注意函数和不等式之间的转化,渗透转化思想。2、提高学生用数学解决实际问题的能力。
(学科整合型问题) 声音在空气中传播的速度y(m/s)(简称声速)是气温x(℃)的一次函数.下表列出了一组不同气温时的声速:(1) 求y与x之间的函数关系式;(2) 气温x=22(℃)时,某人看到烟花燃放5s后才听到声响,那么此人与燃放的烟花所在地约相距多远? 请同学们回忆声音在空气中的传播速度和温度之间的关系。用待定系数法求函数解析式。3、能不能找到一种更方便的解题方法。 1、引起兴趣。2、体现直观性原则
四、课堂小结
(1)这节课我们学习了哪些数学思想和解题方法?
(2)经过这节课的学习,你有哪些收获?
五、作业:见课后练习。
