第三单元解决问题的策略必考题检测卷(单元测试)-小学数学六年级下册苏教版(含答案)
文档属性
| 名称 | 第三单元解决问题的策略必考题检测卷(单元测试)-小学数学六年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-16 12:27:48 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三单元解决问题的策略必考题检测卷(单元测试)-小学数学六年级下册苏教版
一、选择题
1.联想大考验:从“新学期,老师给同学们发书,发了一部分后,已发的书是未发书的。”中,分析出下列几句话,其中准确的有( )句?
①已发了②还有没有发③已发与未发的书的比是1∶4④已发的书比未发的书少
A.1 B.2 C.3 D.4
2.如果一个三角形三个内角度数的比是1∶2∶3,这个三角形是( )三角形。
A.不确定 B.钝角 C.锐角 D.直角
3.一本故事书已看的页数和未看页数的比是2∶3,下面说法错误的是( )。
A.已看的页数是未看页数的 B.已看的页数比未看的页数少
C.已看了全书页数的 D.全书还有没有看
4.小王、小李和小张同时各做120个同样的机器零件,当小王做完时,小李做了100个,小张做了60个,照这样计算,小李做完时,小张没做的有( )个。
A.48 B.40 C.20 D.60
5.三轮车和自行车一共有10辆,数一数它们的轮子一共有27个。自行车有( )辆。
A.5 B.4 C.6 D.3
6.青云酒店有3人房和2人房共50间,总共可以住112位客人,则该酒店有( )。
A.3人房12间,2人房38间 B.3人房20间,2人房26间
C.3人房16间,2人房34间 D.3人房8间,2人房42间
二、填空题
7.师傅比徒弟多做,师徒做的数量比是( ),徒弟做的是师傅的。
8.在一次数学测试中,小华与小军的成绩比是5∶4,已知小华比小军多考了18分,那么小军考了( )分,两人一共考了( )分。
9.安全知识竞赛共15道题,答对一道题得10分,答错一道题倒扣5分。小云做了所有的题,得了120分,她答对了( )道题。
10.一瓶牛奶喝了,还剩( )。已喝的牛奶和剩下的牛奶的比是(____∶____),已喝的比剩下的少( )。如果还剩600毫升,则喝了( )毫升;如果喝了的比剩下的少600毫升,则还剩( )毫升。
11.大小两个圆的面积和是1500平方厘米。已知两个圆的直径比是2∶1,那么大圆的面积是( )平方厘米,小圆的面积是( )平方厘米。
12.如下图,长方形A和B有一部分重合。阴影部分的面积占A的,占B的。那么长方形A与B的面积比是(____∶____)。
13.六(1)班男生人数是女生的,女生人数是男生的( ),女生人数是总人数的( )。如果六(1)班的总人数在40~50之间,那么六(1)班一共有( )人。
14.业余时间小丽看了一本课外书的,还剩没有看完,已看和没看的课外书之比是( )∶( )。
三、判断题
15.一杯果汁喝掉,喝掉的是剩下的. ( )
16.两个圆的直径比是3∶1,则它们的面积比就是9∶1。( )
17.如果男生人数比女生人数多,那么女生人数就比男生人数少.( )
18.鸡兔同笼,有23个头,56条腿,则鸡有23只。( )
19.鸡兔同笼,从上面数有10个头,从下面数有28只脚.鸡有7只,兔有3只。( )
四、计算题
20.直接写得数。
21.计算下列各题,能简算的要简算。
24÷ ×÷× 13.92-(1.19+9.42)-2.81
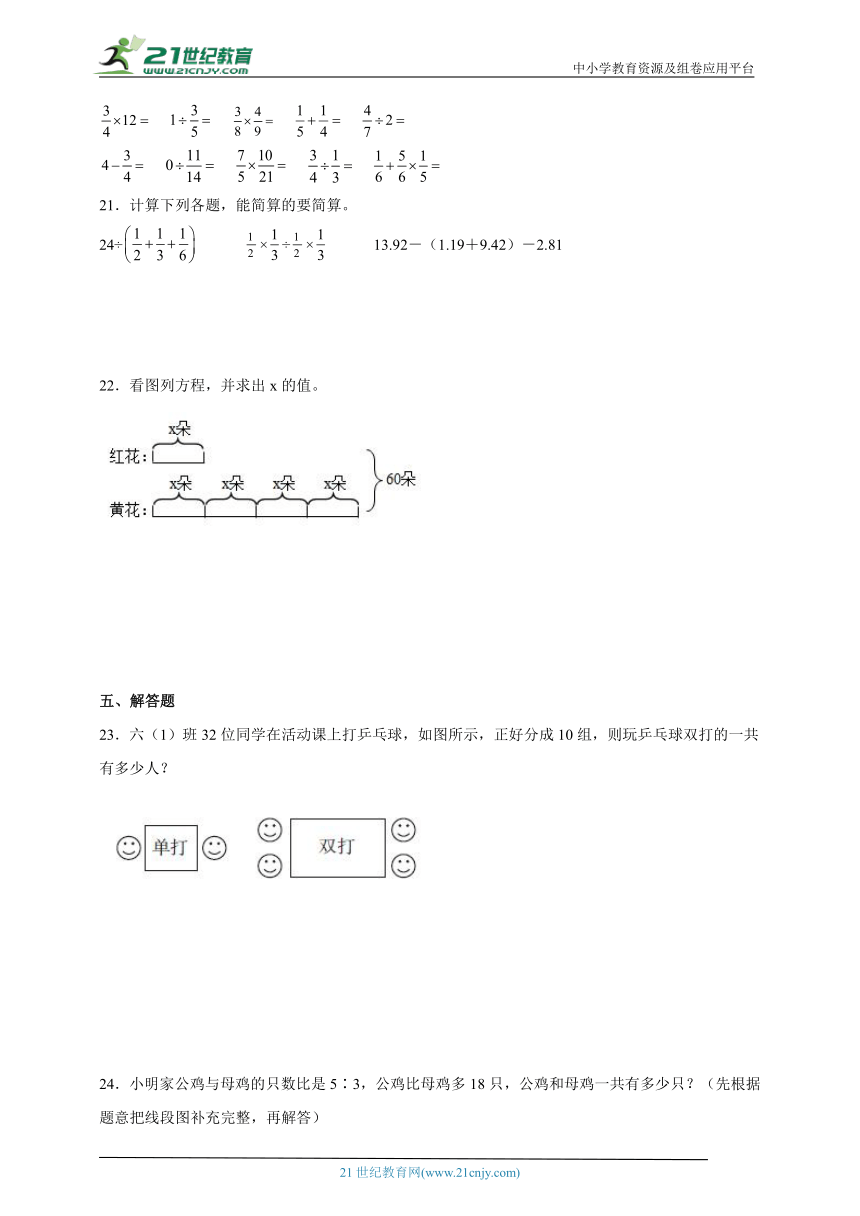
22.看图列方程,并求出x的值。
五、解答题
23.六(1)班32位同学在活动课上打乒乓球,如图所示,正好分成10组,则玩乒乓球双打的一共有多少人?
24.小明家公鸡与母鸡的只数比是5∶3,公鸡比母鸡多18只,公鸡和母鸡一共有多少只?(先根据题意把线段图补充完整,再解答)
25.奇思同学参加了环保知识竞赛,共答了20 道题,答对一题得5分,答错一题倒扣2分,奇思得了79分,他答对了几道题?
26.5月31 日是世界无烟日,希望小学开展禁烟宣传活动,同学们跳起了“无烟小苹果”广场舞,跳舞人数在220~230人之间,跳舞的男生人数是女生人数的。跳广场舞的男、女生各有多少人?
27.赵老师骑车行一段3600米的路,其中一段平路每分钟行200米,一段上坡路每分钟行80米,行完全程用30分钟。平路用了多少分钟?原路返回时,若下坡路每分钟行250米,整个返回过程需要多少分钟?
参考答案:
1.B
【分析】根据题意,从“老师给同学们发书,发了一部分后,已发的书是未发书的。”中,可以了解到的信息有:①已发了;②还有没有发;③已发与未发的书的比是1∶4④已发的书比未发的书少,据此解答即可。
【详解】分析题中几句话,其中准确的有①已发了和③已发与未发的书的比是1∶4,所以准确的有2句。
故答案为:B
【点睛】本题考查了分数应用题以及比的意义和应用知识,结合题意分析解答即可。
2.D
【分析】三角形三个内角度数的比是1∶2∶3,把三角形的三个角度数分别看作1份、2份、3份,则最大角占内角和的,再根据最大角来判断三角形的类型即可。
【详解】
(度)
三角形是直角三角形。
故答案为:D
【点睛】本题考查按比例分配、以及三角形的类型,解答本题的关键是掌握按比例分配解决问题的方法。
3.B
【分析】已看的页数和未看页数的比是2∶3,把已看的页数看作2份,为看的页数看作3份,再判断每个选项的说法正确与否即可。
【详解】已看的页数是未看页数、已看了全书页数的、全书还有没有看三种说法都正确;
(3-2)÷3=,即已看的页数比未看的页数少,因此,已看的页数比未看的页数少说法不正确;
故选:B。
【点睛】本题考查比的意义,解答本题的关键是掌握比的概念。
4.A
【分析】因为在同一时间内,小李做了100个,小张只做了60个,所以两人的“工效”之比是5∶3;因此小李再做20个时,小张只能做20×=12(个),所以小张还有120-60-12=48个没有做完。
【详解】两人的“工效”之比是100∶60=5∶3
120-60-(120-100)×
=120-60-12
=48(个)
答:小李做完时,小张还差48个没做。
故答案为:A
【点睛】此题主要考查了工程问题的应用,关键是求出小李和小张两人的“工效”之比。
5.D
【分析】假设全是三轮车,求出应有的轮子减去实际的轮子的差除以三轮车与自行车的轮子之差,得出自行车的辆数。
【详解】(3×10-27)÷(3-2)
=3÷1
=3(辆),自行车有3辆。
故选择:D。
【点睛】此题属于典型的鸡兔同笼问题,也可通过方程、枚举法来解答。
6.A
【分析】假设全是3人房,则一共可以住50×3=150人,这比已知的112人多出了150-112=38人,因为一间3人房比1间2人房多3-2=1人;所以2人间一共有38间,则3人房有50-38=12间。
【详解】假设全是3人房,则2人房有:
(50×3-112)÷(3-2)
=38÷1
=38(间)
则3人房有:50-38=12(间)
故答案为:A
【点睛】此题属于鸡兔同笼问题,采用假设法直接计算出正确结果,再进行选择即可。
7.5∶4;
【分析】由题意,根据师傅比徒弟多做,徒弟做的数量是单位“1”,则师傅做的为1+=,则师徒做的数量比是1∶=5∶4;求徒弟做的是徒弟的几分之几,直接用1÷计算即可;据此解答
【详解】1∶(1+)=5∶4,
1÷=1×=,
所以师徒做的数量比是5∶4,徒弟做的是师傅的。
【点睛】本题主要考查对解决问题的策略知识点的灵活运用,解题关键是找到单位“1”。
8. 72 162
【分析】小华与小军两人的成绩比是5∶4,把成绩之比看作份数比,已知小华比小军多考了18分,则多的5-4=1份为18,则小军考了18×4=72分,一共考了18×(5+4)=162分,据此解答即可。
【详解】18÷(5-4)×4
=18×4
=72(分)
18×(5+4)
=18×9
=162(分)
【点睛】解答此题关键是把比转化为份数,先求1份数,再求几份数。
9.13
【分析】此题主要考查了鸡兔同笼的应用题,可以列方程解答,设小云答对x题,则答错(15-x)题,用答对一题的得分×答对的题数-答错一题扣的分×答错的题数=实际得分,据此列方程解答。
【详解】解:设小云答对x题,则答错(15-x)题。
10x-5×(15-x)=120
10x-5×15+5x=120
15x-5×15=120
15x-75=120
15x-75+75=120+75
15x=195
15x÷15=195÷15
x=13
【点睛】此题主要考查了学生列方程解答鸡兔同笼问题的能力,设其中一个未知数为x,另一个未知数用含x的式子表示,以此进行解方程。
10. 1 3 200 900
【分析】把这瓶牛奶看作单位“1”,还剩的=1-;表示出已喝的和剩下的牛奶写成比的形式,化到最简;剩下的与已喝的差除以剩下的即可;根据已喝的牛奶和剩下的牛奶的比,还剩的600毫升除以后项得出1份的毫升数,再乘以前项就是喝了的毫升数;根据已喝的牛奶和剩下的牛奶的比,喝的与剩下的毫升数之差除以后项与前项之差,得出1份的量,乘后项即可。
【详解】1-=,一瓶牛奶喝了,还剩;∶化简得1∶3,已喝的牛奶和剩下的牛奶的比是1∶3;(-)÷=÷=,已喝的比剩下的少;600÷3×1=200(毫升),如果还剩600毫升,则喝了200毫升;600÷(3-1)×3=900(毫升),如果喝了的比剩下的少600毫升,则还剩900毫升。
【点睛】解答此题关键是根据已喝的占总数的几分之几,求出已喝的与剩下的之间的比,由题目中所给具体数量找出1份的量,再来求其它的量。
11. 1200 300
【分析】两圆的面积比等于半径平方的比,半径比等于直径比,根据直径比计算出两圆的面积比,再按比例分配求出两圆各自的面积。
【详解】两个圆的直径比是2∶1,则半径比也是2∶1,那么它们的面积比是4∶1,已知两圆面积和是1500平方厘米。
则大圆面积是1500× =1200(平方厘米)
小圆面积是1500×=300(平方厘米)
【点睛】此题考查圆的面积与比的综合应用,根据两圆直径比找出两圆面积比是解题关键。
12. 2 3
【分析】假设阴影部分的面积为1,则长方形A的面积为3,长方形B的面积为,据此表示出长方形A与B的面积之比。
【详解】设阴影部分的面积为1。
长方形A的面积:1÷=3
长方形B的面积:1÷=
长方形A与B的面积之比是:
3∶
=(3×2)∶(×2)
=6∶9
=(6÷3)∶(9÷3)
=2∶3
【点睛】解答此题的关键是根据中间量阴影部分的面积,找出长方形A与B的关系。
13. 45
【分析】把女生人数看作单位“1”,则男生人数为,女生人数除以男生人数是女生人数是男生人数的几分之几,根据男生人数与女生人数的关系,得出女生人数与男生人数的比,从而得出女生人数和总人数的比,根据女生人数和总人数的比,前项除以后项即可;根据女生人数和总人数的比,总人数在40~50之间,后项的倍数即可。
【详解】1÷=,六(1)班男生人数是女生的,女生人数是男生的;女生人数与男生人数的比1∶化简得4∶5,所以女生人数与总人数的比是4∶9,4÷9=,女生人数是总人数的,40~50之间,9的倍数是45,所以那么六(1)班一共有45人。
【点睛】找准单位“1”,进而找出男生、女生以及全班人数之间的关系,是解题关键。
14.;;3;1
【分析】把一本课外书看成是单位“1”,由图可知,把这本课外书平均分成4份,涂色的部分(已看)有3份,空白部分(没看)有1份。据此即可解答。
【详解】已看这本书的3÷4=;还剩:1÷4=;已看和没看的课外书之比是3∶1。
【点睛】熟练掌握一个量占另一个量的几分之几,用除法。此题通过图形中给出信息进行列式解答,体现了数形结合的思想。
15.×
【详解】略
16.√
【分析】两圆的直径比就等于两圆的半径比,而圆的面积比等于半径的平方比,按此计算解答即可。
【详解】由两圆的直径比是3∶1,可得两圆的半径比也为3∶1,而圆的面积比等于半径的平方比,所以它们的面积比是32∶12=9∶1。
故答案为:√
【点睛】此题关键是知道圆的面积比等于半径的平方比这一知识点。也可以设两圆的直径分别是3和1,然后计算它们的面积后相比。
17.×
【详解】略
18.×
【分析】用假设法来解,先把23个头全看成是兔的,多出的腿数的正好是把鸡看成了兔而多出的,一只鸡多算(4-2)条腿,看多出的腿里有多少份(4-2)条腿,也就求出鸡的只数。
【详解】(23×4-56)÷(4-2)
=36÷2
=18(只)
鸡有18只,原题说法错误。
故答案为:×
19.×
【详解】(10×4-28)÷(4-2)
=12÷2
=6(只)
兔:10-6=4(只),原题计算错误。
故答案为:×
【点睛】假设都是兔子,则有10×4只脚,一定比28多,是因为把鸡也当作兔来计算了,用多算的脚的只数除以每只兔子比每只鸡多的脚的只数即可求出鸡的只数,进而求出兔子的只数即可。
20.9;;;;
;0;;;
【详解】略
21.24;;0.5
【分析】第一个算式,根据四则混合运算顺序解答;
第二个算式,运用乘法交换率和乘法结合律进行简算;
第三个算式,运用减法的性质简算。
【详解】24÷
=24÷1
=24
×÷×
=×
=
13.92-(1.19+9.42)-2.81
=13.92-9.42-1.19-2.81
=13.92-9.42-(1.19+2.81)
=4.5-4
=0.5
【点睛】此题是考查四则混合运算,要仔细观察算式的特点,灵活运用一些定律进行简便计算。
22.12朵
【分析】根据图可知,红花x朵,黄花有4个x朵,即4x朵,由于红花的数量+黄花的数量=60,由此即可列方程,再根据等式的性质解方程即可。
【详解】x+4x=60
解:5x=60
x=60÷5
x=12
23.24人
【详解】假设全玩双打:(4×10-32)÷(4-2)=4(组)
10-4=6(组)
6×4=24(人)
答:玩乒乓球双打的一共有24人。
24.如图所示:
;72只
【详解】18÷(5-3)×(5+3)=72(只)答:公鸡和母鸡一共有72只。
25.17道
【详解】(20×5-79)÷(2+5)=3(道)
20-3=17(道)
答:他答对了17道题。
26.男生100人;女生125人。
【详解】4+5=9,因为在220~230之间是9的倍数的数是225,所以跳广场舞的学生总人数是225人。
男生:225×=100(人)
女生:225×=125(人)
答:跳广场舞的男生有100人,女生有125人。
27.10分钟;16.4分钟
【详解】(3600-30×80)÷(200-80)=10(分钟)
10+(3600-10×200)÷250=16.4(分钟)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三单元解决问题的策略必考题检测卷(单元测试)-小学数学六年级下册苏教版
一、选择题
1.联想大考验:从“新学期,老师给同学们发书,发了一部分后,已发的书是未发书的。”中,分析出下列几句话,其中准确的有( )句?
①已发了②还有没有发③已发与未发的书的比是1∶4④已发的书比未发的书少
A.1 B.2 C.3 D.4
2.如果一个三角形三个内角度数的比是1∶2∶3,这个三角形是( )三角形。
A.不确定 B.钝角 C.锐角 D.直角
3.一本故事书已看的页数和未看页数的比是2∶3,下面说法错误的是( )。
A.已看的页数是未看页数的 B.已看的页数比未看的页数少
C.已看了全书页数的 D.全书还有没有看
4.小王、小李和小张同时各做120个同样的机器零件,当小王做完时,小李做了100个,小张做了60个,照这样计算,小李做完时,小张没做的有( )个。
A.48 B.40 C.20 D.60
5.三轮车和自行车一共有10辆,数一数它们的轮子一共有27个。自行车有( )辆。
A.5 B.4 C.6 D.3
6.青云酒店有3人房和2人房共50间,总共可以住112位客人,则该酒店有( )。
A.3人房12间,2人房38间 B.3人房20间,2人房26间
C.3人房16间,2人房34间 D.3人房8间,2人房42间
二、填空题
7.师傅比徒弟多做,师徒做的数量比是( ),徒弟做的是师傅的。
8.在一次数学测试中,小华与小军的成绩比是5∶4,已知小华比小军多考了18分,那么小军考了( )分,两人一共考了( )分。
9.安全知识竞赛共15道题,答对一道题得10分,答错一道题倒扣5分。小云做了所有的题,得了120分,她答对了( )道题。
10.一瓶牛奶喝了,还剩( )。已喝的牛奶和剩下的牛奶的比是(____∶____),已喝的比剩下的少( )。如果还剩600毫升,则喝了( )毫升;如果喝了的比剩下的少600毫升,则还剩( )毫升。
11.大小两个圆的面积和是1500平方厘米。已知两个圆的直径比是2∶1,那么大圆的面积是( )平方厘米,小圆的面积是( )平方厘米。
12.如下图,长方形A和B有一部分重合。阴影部分的面积占A的,占B的。那么长方形A与B的面积比是(____∶____)。
13.六(1)班男生人数是女生的,女生人数是男生的( ),女生人数是总人数的( )。如果六(1)班的总人数在40~50之间,那么六(1)班一共有( )人。
14.业余时间小丽看了一本课外书的,还剩没有看完,已看和没看的课外书之比是( )∶( )。
三、判断题
15.一杯果汁喝掉,喝掉的是剩下的. ( )
16.两个圆的直径比是3∶1,则它们的面积比就是9∶1。( )
17.如果男生人数比女生人数多,那么女生人数就比男生人数少.( )
18.鸡兔同笼,有23个头,56条腿,则鸡有23只。( )
19.鸡兔同笼,从上面数有10个头,从下面数有28只脚.鸡有7只,兔有3只。( )
四、计算题
20.直接写得数。
21.计算下列各题,能简算的要简算。
24÷ ×÷× 13.92-(1.19+9.42)-2.81
22.看图列方程,并求出x的值。
五、解答题
23.六(1)班32位同学在活动课上打乒乓球,如图所示,正好分成10组,则玩乒乓球双打的一共有多少人?
24.小明家公鸡与母鸡的只数比是5∶3,公鸡比母鸡多18只,公鸡和母鸡一共有多少只?(先根据题意把线段图补充完整,再解答)
25.奇思同学参加了环保知识竞赛,共答了20 道题,答对一题得5分,答错一题倒扣2分,奇思得了79分,他答对了几道题?
26.5月31 日是世界无烟日,希望小学开展禁烟宣传活动,同学们跳起了“无烟小苹果”广场舞,跳舞人数在220~230人之间,跳舞的男生人数是女生人数的。跳广场舞的男、女生各有多少人?
27.赵老师骑车行一段3600米的路,其中一段平路每分钟行200米,一段上坡路每分钟行80米,行完全程用30分钟。平路用了多少分钟?原路返回时,若下坡路每分钟行250米,整个返回过程需要多少分钟?
参考答案:
1.B
【分析】根据题意,从“老师给同学们发书,发了一部分后,已发的书是未发书的。”中,可以了解到的信息有:①已发了;②还有没有发;③已发与未发的书的比是1∶4④已发的书比未发的书少,据此解答即可。
【详解】分析题中几句话,其中准确的有①已发了和③已发与未发的书的比是1∶4,所以准确的有2句。
故答案为:B
【点睛】本题考查了分数应用题以及比的意义和应用知识,结合题意分析解答即可。
2.D
【分析】三角形三个内角度数的比是1∶2∶3,把三角形的三个角度数分别看作1份、2份、3份,则最大角占内角和的,再根据最大角来判断三角形的类型即可。
【详解】
(度)
三角形是直角三角形。
故答案为:D
【点睛】本题考查按比例分配、以及三角形的类型,解答本题的关键是掌握按比例分配解决问题的方法。
3.B
【分析】已看的页数和未看页数的比是2∶3,把已看的页数看作2份,为看的页数看作3份,再判断每个选项的说法正确与否即可。
【详解】已看的页数是未看页数、已看了全书页数的、全书还有没有看三种说法都正确;
(3-2)÷3=,即已看的页数比未看的页数少,因此,已看的页数比未看的页数少说法不正确;
故选:B。
【点睛】本题考查比的意义,解答本题的关键是掌握比的概念。
4.A
【分析】因为在同一时间内,小李做了100个,小张只做了60个,所以两人的“工效”之比是5∶3;因此小李再做20个时,小张只能做20×=12(个),所以小张还有120-60-12=48个没有做完。
【详解】两人的“工效”之比是100∶60=5∶3
120-60-(120-100)×
=120-60-12
=48(个)
答:小李做完时,小张还差48个没做。
故答案为:A
【点睛】此题主要考查了工程问题的应用,关键是求出小李和小张两人的“工效”之比。
5.D
【分析】假设全是三轮车,求出应有的轮子减去实际的轮子的差除以三轮车与自行车的轮子之差,得出自行车的辆数。
【详解】(3×10-27)÷(3-2)
=3÷1
=3(辆),自行车有3辆。
故选择:D。
【点睛】此题属于典型的鸡兔同笼问题,也可通过方程、枚举法来解答。
6.A
【分析】假设全是3人房,则一共可以住50×3=150人,这比已知的112人多出了150-112=38人,因为一间3人房比1间2人房多3-2=1人;所以2人间一共有38间,则3人房有50-38=12间。
【详解】假设全是3人房,则2人房有:
(50×3-112)÷(3-2)
=38÷1
=38(间)
则3人房有:50-38=12(间)
故答案为:A
【点睛】此题属于鸡兔同笼问题,采用假设法直接计算出正确结果,再进行选择即可。
7.5∶4;
【分析】由题意,根据师傅比徒弟多做,徒弟做的数量是单位“1”,则师傅做的为1+=,则师徒做的数量比是1∶=5∶4;求徒弟做的是徒弟的几分之几,直接用1÷计算即可;据此解答
【详解】1∶(1+)=5∶4,
1÷=1×=,
所以师徒做的数量比是5∶4,徒弟做的是师傅的。
【点睛】本题主要考查对解决问题的策略知识点的灵活运用,解题关键是找到单位“1”。
8. 72 162
【分析】小华与小军两人的成绩比是5∶4,把成绩之比看作份数比,已知小华比小军多考了18分,则多的5-4=1份为18,则小军考了18×4=72分,一共考了18×(5+4)=162分,据此解答即可。
【详解】18÷(5-4)×4
=18×4
=72(分)
18×(5+4)
=18×9
=162(分)
【点睛】解答此题关键是把比转化为份数,先求1份数,再求几份数。
9.13
【分析】此题主要考查了鸡兔同笼的应用题,可以列方程解答,设小云答对x题,则答错(15-x)题,用答对一题的得分×答对的题数-答错一题扣的分×答错的题数=实际得分,据此列方程解答。
【详解】解:设小云答对x题,则答错(15-x)题。
10x-5×(15-x)=120
10x-5×15+5x=120
15x-5×15=120
15x-75=120
15x-75+75=120+75
15x=195
15x÷15=195÷15
x=13
【点睛】此题主要考查了学生列方程解答鸡兔同笼问题的能力,设其中一个未知数为x,另一个未知数用含x的式子表示,以此进行解方程。
10. 1 3 200 900
【分析】把这瓶牛奶看作单位“1”,还剩的=1-;表示出已喝的和剩下的牛奶写成比的形式,化到最简;剩下的与已喝的差除以剩下的即可;根据已喝的牛奶和剩下的牛奶的比,还剩的600毫升除以后项得出1份的毫升数,再乘以前项就是喝了的毫升数;根据已喝的牛奶和剩下的牛奶的比,喝的与剩下的毫升数之差除以后项与前项之差,得出1份的量,乘后项即可。
【详解】1-=,一瓶牛奶喝了,还剩;∶化简得1∶3,已喝的牛奶和剩下的牛奶的比是1∶3;(-)÷=÷=,已喝的比剩下的少;600÷3×1=200(毫升),如果还剩600毫升,则喝了200毫升;600÷(3-1)×3=900(毫升),如果喝了的比剩下的少600毫升,则还剩900毫升。
【点睛】解答此题关键是根据已喝的占总数的几分之几,求出已喝的与剩下的之间的比,由题目中所给具体数量找出1份的量,再来求其它的量。
11. 1200 300
【分析】两圆的面积比等于半径平方的比,半径比等于直径比,根据直径比计算出两圆的面积比,再按比例分配求出两圆各自的面积。
【详解】两个圆的直径比是2∶1,则半径比也是2∶1,那么它们的面积比是4∶1,已知两圆面积和是1500平方厘米。
则大圆面积是1500× =1200(平方厘米)
小圆面积是1500×=300(平方厘米)
【点睛】此题考查圆的面积与比的综合应用,根据两圆直径比找出两圆面积比是解题关键。
12. 2 3
【分析】假设阴影部分的面积为1,则长方形A的面积为3,长方形B的面积为,据此表示出长方形A与B的面积之比。
【详解】设阴影部分的面积为1。
长方形A的面积:1÷=3
长方形B的面积:1÷=
长方形A与B的面积之比是:
3∶
=(3×2)∶(×2)
=6∶9
=(6÷3)∶(9÷3)
=2∶3
【点睛】解答此题的关键是根据中间量阴影部分的面积,找出长方形A与B的关系。
13. 45
【分析】把女生人数看作单位“1”,则男生人数为,女生人数除以男生人数是女生人数是男生人数的几分之几,根据男生人数与女生人数的关系,得出女生人数与男生人数的比,从而得出女生人数和总人数的比,根据女生人数和总人数的比,前项除以后项即可;根据女生人数和总人数的比,总人数在40~50之间,后项的倍数即可。
【详解】1÷=,六(1)班男生人数是女生的,女生人数是男生的;女生人数与男生人数的比1∶化简得4∶5,所以女生人数与总人数的比是4∶9,4÷9=,女生人数是总人数的,40~50之间,9的倍数是45,所以那么六(1)班一共有45人。
【点睛】找准单位“1”,进而找出男生、女生以及全班人数之间的关系,是解题关键。
14.;;3;1
【分析】把一本课外书看成是单位“1”,由图可知,把这本课外书平均分成4份,涂色的部分(已看)有3份,空白部分(没看)有1份。据此即可解答。
【详解】已看这本书的3÷4=;还剩:1÷4=;已看和没看的课外书之比是3∶1。
【点睛】熟练掌握一个量占另一个量的几分之几,用除法。此题通过图形中给出信息进行列式解答,体现了数形结合的思想。
15.×
【详解】略
16.√
【分析】两圆的直径比就等于两圆的半径比,而圆的面积比等于半径的平方比,按此计算解答即可。
【详解】由两圆的直径比是3∶1,可得两圆的半径比也为3∶1,而圆的面积比等于半径的平方比,所以它们的面积比是32∶12=9∶1。
故答案为:√
【点睛】此题关键是知道圆的面积比等于半径的平方比这一知识点。也可以设两圆的直径分别是3和1,然后计算它们的面积后相比。
17.×
【详解】略
18.×
【分析】用假设法来解,先把23个头全看成是兔的,多出的腿数的正好是把鸡看成了兔而多出的,一只鸡多算(4-2)条腿,看多出的腿里有多少份(4-2)条腿,也就求出鸡的只数。
【详解】(23×4-56)÷(4-2)
=36÷2
=18(只)
鸡有18只,原题说法错误。
故答案为:×
19.×
【详解】(10×4-28)÷(4-2)
=12÷2
=6(只)
兔:10-6=4(只),原题计算错误。
故答案为:×
【点睛】假设都是兔子,则有10×4只脚,一定比28多,是因为把鸡也当作兔来计算了,用多算的脚的只数除以每只兔子比每只鸡多的脚的只数即可求出鸡的只数,进而求出兔子的只数即可。
20.9;;;;
;0;;;
【详解】略
21.24;;0.5
【分析】第一个算式,根据四则混合运算顺序解答;
第二个算式,运用乘法交换率和乘法结合律进行简算;
第三个算式,运用减法的性质简算。
【详解】24÷
=24÷1
=24
×÷×
=×
=
13.92-(1.19+9.42)-2.81
=13.92-9.42-1.19-2.81
=13.92-9.42-(1.19+2.81)
=4.5-4
=0.5
【点睛】此题是考查四则混合运算,要仔细观察算式的特点,灵活运用一些定律进行简便计算。
22.12朵
【分析】根据图可知,红花x朵,黄花有4个x朵,即4x朵,由于红花的数量+黄花的数量=60,由此即可列方程,再根据等式的性质解方程即可。
【详解】x+4x=60
解:5x=60
x=60÷5
x=12
23.24人
【详解】假设全玩双打:(4×10-32)÷(4-2)=4(组)
10-4=6(组)
6×4=24(人)
答:玩乒乓球双打的一共有24人。
24.如图所示:
;72只
【详解】18÷(5-3)×(5+3)=72(只)答:公鸡和母鸡一共有72只。
25.17道
【详解】(20×5-79)÷(2+5)=3(道)
20-3=17(道)
答:他答对了17道题。
26.男生100人;女生125人。
【详解】4+5=9,因为在220~230之间是9的倍数的数是225,所以跳广场舞的学生总人数是225人。
男生:225×=100(人)
女生:225×=125(人)
答:跳广场舞的男生有100人,女生有125人。
27.10分钟;16.4分钟
【详解】(3600-30×80)÷(200-80)=10(分钟)
10+(3600-10×200)÷250=16.4(分钟)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
