18.3 一次函数[下学期]
图片预览




文档简介
课件22张PPT。 一次函数复习课授课:初二年数学备课组
苏春树一、函数的表示法二、一次函数的表达式正比例函数是一次函数,而一次函数不一定是正比例函数.正比例函数是一次函数的特殊情况. 三、一次函数的图象y=kx+b的图象是一条 。直线画图时,一般取两个点 。 (0,b)和(-b/k,0)你能求出直线y= -5x-16
与坐标轴的交点坐标吗?A·00-3.2-16探索发现
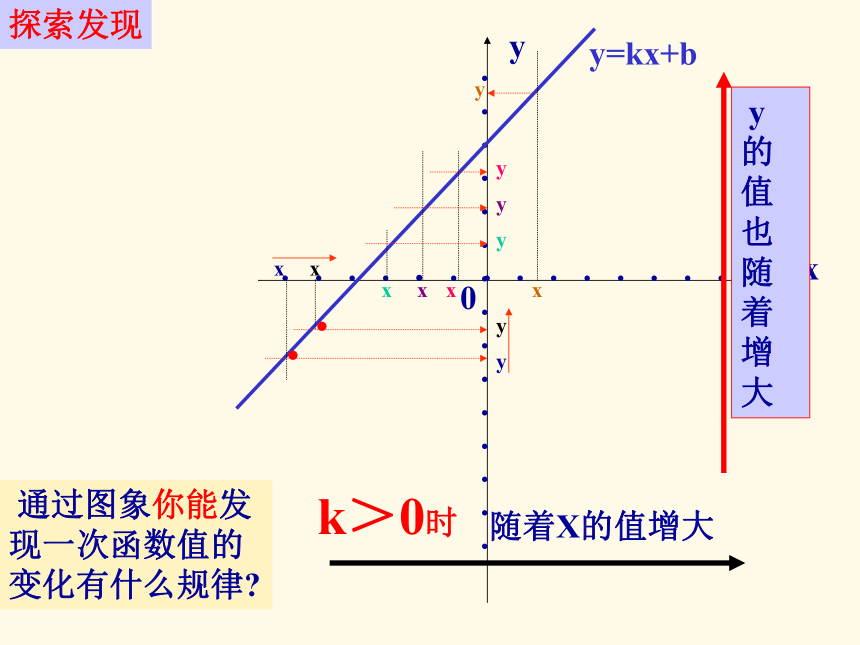
k>0时 通过图象你能发现一次函数值的变化有什么规律?··探索发现
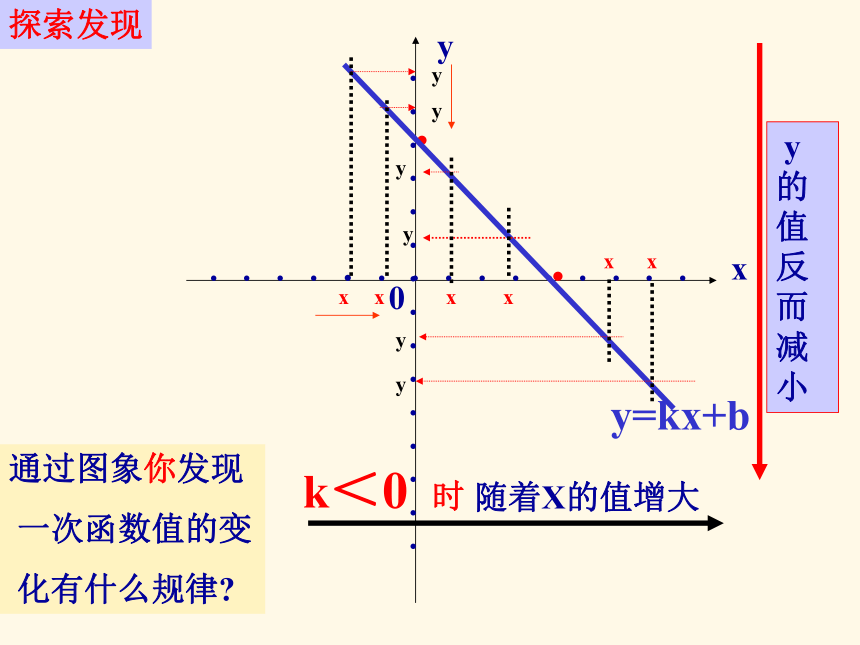
··k<0 时通过图象你发现
一次函数值的变
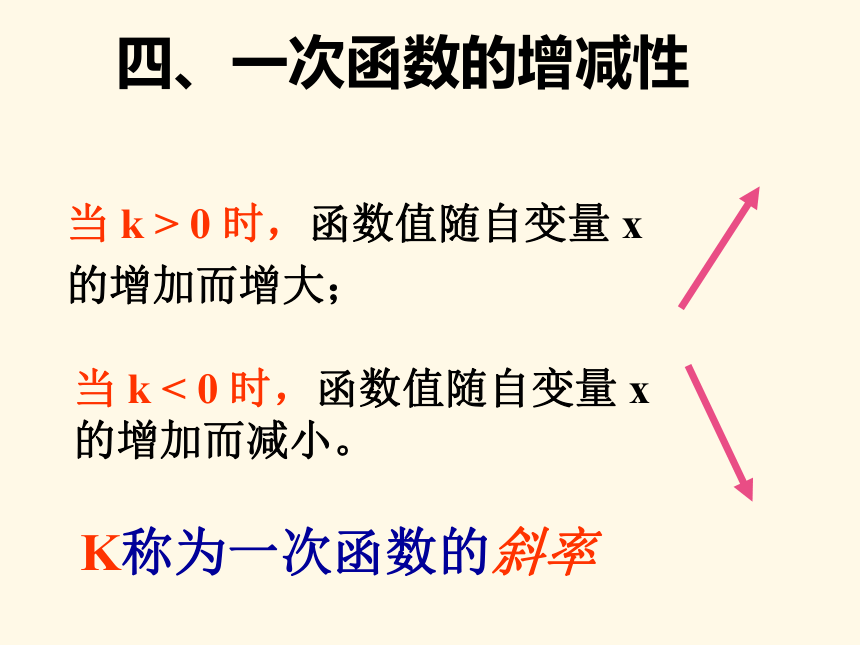
化有什么规律?四、一次函数的增减性当 k < 0 时,函数值随自变量 x 的增加而减小。当 k > 0 时,函数值随自变量 x
的增加而增大;K称为一次函数的斜率
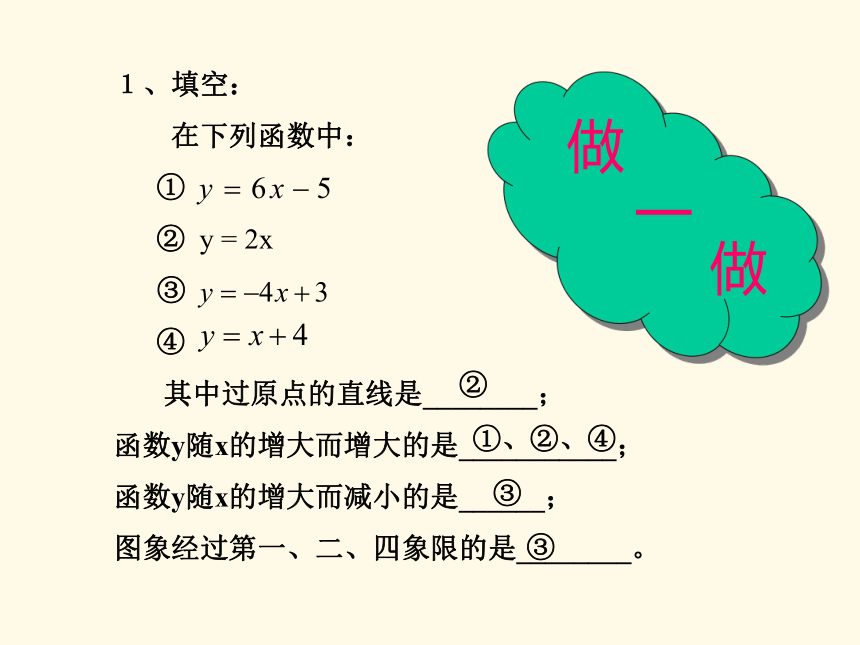
1、填空:
在下列函数中:
①
② y = 2x
③
④
其中过原点的直线是________;
函数y随x的增大而增大的是___________;
函数y随x的增大而减小的是______;
图象经过第一、二、四象限的是________。②①、②、④③③做一做直线y=kx+b 动手做一做 探索发现规律经过画图你
发现一次函
数图象的什
么规律?1-33212-1-2-1-2直线y=kx+b探索发现
····经过画图你发现
直线与x轴所成的
锐角大小与什么有关?1 11-0.5-1y=-2x+1直线y=kx+by=-4x+1y=-x+1探索发现
····y=-1x+1y=-2x+1y=-4x+1经过画图你发现
直线与x轴所成的
锐角大小与什么有关?11这三个函数的图象还有什么共同特点?K叫做斜率, b叫做截距直线y=kx+b2、解:图(1)中k>0,b=0;
图(2)中k<0,b=0;
图(3)中k<0,b>0;
图(4)中k<0,b<0. K和b决定了一次函数的图象和性质思考:若点(2,-1)在函数y=kx+b图象上,你能求出它的解析式吗?如果(0,3)也在它的图象上,那能求吗?y=-2x+3y=-2x+3与y=2x+1的图象的位置有何关系?你能求出交点的坐标吗?(0.5,2)试求y=-2x+3与y=2x+1以及x轴所围成的三角形的面积?11322-1(0.5,2)(1.5,0)(-0.5,0)试求y=-2x+3与y=2x+1以及x轴所围成的三角形的面积?S=1/2×(0.5+1.5)×2
=2学好函数的关键是图象.我们要学会从函数图象中分析、获取有用的信息,来帮助我们解题。某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。(1)服药后______时,血液中含药量最高,
达到每毫升_______毫克,接着逐步衰弱。(2)服药5时,血液中含药量为每毫升____毫克。(3)当x≤2时y与x之间的函数关系式是 。
(4)当x≥2时y与x之间的函数关系式是 。y= 3xy= -x+8(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间范围是 时。.41 一农民带了若干千克自产的土豆进城销售,为了方便,他带了一些零钱备用,按照市场价售出一些后,又降价销售,售出的土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,根据图象回答下列问题:(1)农民自带的零钱是多少?
(2)降价前他每千克土豆的售价是多少?
(3)降价后他按每千克0.4元
将剩余的土豆售完,这时他
手中的钱(含备用零钱)
是26元,他一共带了
多少千克土豆?练习:再见2006年3月李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分种,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校。在课堂上,李老师请学生画出自行车行进路程S(千米)与行进时间t(小时)的函数图象的示意图,同学们画出的示意图如下,你认为正确的是( )
问:(1)如果李老师在修好车后减慢速度,但仍匀速行驶,请问该选哪个答案。(2)请修改题目,使其答案为A(或B)。C再见2006年3月已知y-1与x成正比例,且x=-2时,y=4,
那么y与x之间的函数关系式为___________。对图象的理解和把握是学好函数的关键
苏春树一、函数的表示法二、一次函数的表达式正比例函数是一次函数,而一次函数不一定是正比例函数.正比例函数是一次函数的特殊情况. 三、一次函数的图象y=kx+b的图象是一条 。直线画图时,一般取两个点 。 (0,b)和(-b/k,0)你能求出直线y= -5x-16
与坐标轴的交点坐标吗?A·00-3.2-16探索发现
k>0时 通过图象你能发现一次函数值的变化有什么规律?··探索发现
··k<0 时通过图象你发现
一次函数值的变
化有什么规律?四、一次函数的增减性当 k < 0 时,函数值随自变量 x 的增加而减小。当 k > 0 时,函数值随自变量 x
的增加而增大;K称为一次函数的斜率
1、填空:
在下列函数中:
①
② y = 2x
③
④
其中过原点的直线是________;
函数y随x的增大而增大的是___________;
函数y随x的增大而减小的是______;
图象经过第一、二、四象限的是________。②①、②、④③③做一做直线y=kx+b 动手做一做 探索发现规律经过画图你
发现一次函
数图象的什
么规律?1-33212-1-2-1-2直线y=kx+b探索发现
····经过画图你发现
直线与x轴所成的
锐角大小与什么有关?1 11-0.5-1y=-2x+1直线y=kx+by=-4x+1y=-x+1探索发现
····y=-1x+1y=-2x+1y=-4x+1经过画图你发现
直线与x轴所成的
锐角大小与什么有关?11这三个函数的图象还有什么共同特点?K叫做斜率, b叫做截距直线y=kx+b2、解:图(1)中k>0,b=0;
图(2)中k<0,b=0;
图(3)中k<0,b>0;
图(4)中k<0,b<0. K和b决定了一次函数的图象和性质思考:若点(2,-1)在函数y=kx+b图象上,你能求出它的解析式吗?如果(0,3)也在它的图象上,那能求吗?y=-2x+3y=-2x+3与y=2x+1的图象的位置有何关系?你能求出交点的坐标吗?(0.5,2)试求y=-2x+3与y=2x+1以及x轴所围成的三角形的面积?11322-1(0.5,2)(1.5,0)(-0.5,0)试求y=-2x+3与y=2x+1以及x轴所围成的三角形的面积?S=1/2×(0.5+1.5)×2
=2学好函数的关键是图象.我们要学会从函数图象中分析、获取有用的信息,来帮助我们解题。某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。(1)服药后______时,血液中含药量最高,
达到每毫升_______毫克,接着逐步衰弱。(2)服药5时,血液中含药量为每毫升____毫克。(3)当x≤2时y与x之间的函数关系式是 。
(4)当x≥2时y与x之间的函数关系式是 。y= 3xy= -x+8(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间范围是 时。.41 一农民带了若干千克自产的土豆进城销售,为了方便,他带了一些零钱备用,按照市场价售出一些后,又降价销售,售出的土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,根据图象回答下列问题:(1)农民自带的零钱是多少?
(2)降价前他每千克土豆的售价是多少?
(3)降价后他按每千克0.4元
将剩余的土豆售完,这时他
手中的钱(含备用零钱)
是26元,他一共带了
多少千克土豆?练习:再见2006年3月李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分种,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校。在课堂上,李老师请学生画出自行车行进路程S(千米)与行进时间t(小时)的函数图象的示意图,同学们画出的示意图如下,你认为正确的是( )
问:(1)如果李老师在修好车后减慢速度,但仍匀速行驶,请问该选哪个答案。(2)请修改题目,使其答案为A(或B)。C再见2006年3月已知y-1与x成正比例,且x=-2时,y=4,
那么y与x之间的函数关系式为___________。对图象的理解和把握是学好函数的关键
