18.3 一次函数[下学期]
图片预览



文档简介
课件9张PPT。一次函数复习一、知识要点: 1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。kx +b≠0=0≠0kx★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,⑵、比例系数_____。1K≠0 2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。0,01,k 一条直线b一条直线4、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。一、三增大二、四减小5、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
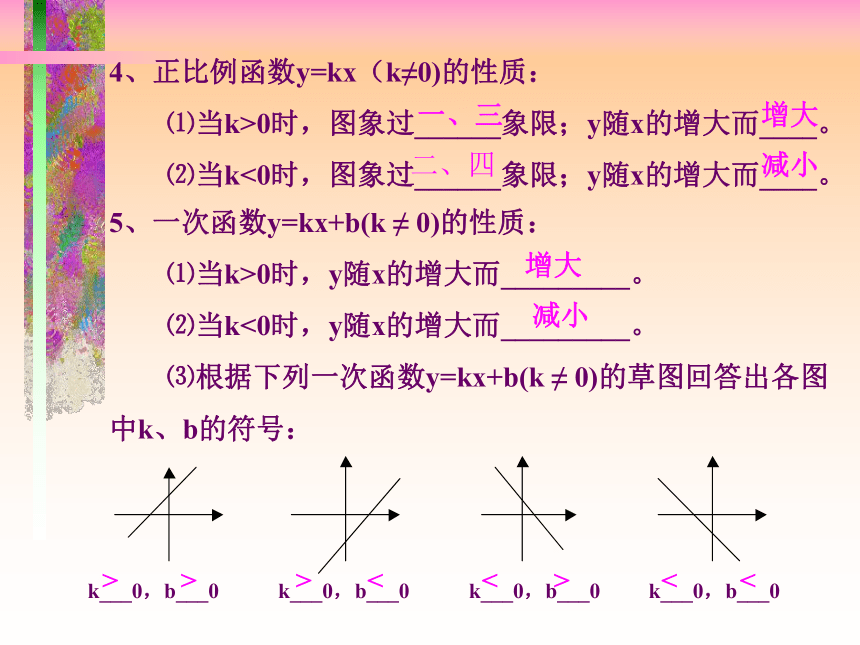
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号:增大减小k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0<<><<>>>②①、②、③④③解:一次函数当x=1时,y=5。且它的图象与x轴交点
是(6,0)。由题意得解得∴一次函数的解析式为 y= - x+6。点评:用待定系数法求一次函数y=kx+b的解析式,可由已知条件给出的两对x、y的值,列出关于k、b的二元一次方程组。由此求出k、b的值,就可以得到所求的一次函数的解析式。例2、已知一次函数y=kx+b(k≠0)在x=1时,y=5,且
它的图象与x轴交点的横坐标是6,求这个一次函数的
解析式。 例3 柴油机在工作时油箱中的余油量Q(千克)
与工作时间t(小时)成一次函数关系,当工作开始时
油箱中有油40千克,工作3.5小时后,油箱中余油22.5
千克(1)写出余油量Q与时间t的函数关系式;(2)画出
这个函数的图象。解:(1)设Q=kt+b。把t=0,Q=40;t=3.5,Q=22.5
分别代入上式,得解得解析式为:Q=-5t+40 (0≤t≤8)(2)、取t=0,得Q=40;取t=8,得Q=0。描出点
A(0,40),B(8,0)。然后连成线段AB即是所
求的图形。点评:(1)求出函数关系式时,
必须找出自变量的取值范围。
(2)画函数图象时,应
根据函数自变量的取值范围来
确定图象的范围。20图象是包括
两端点的线段..AB2,00,1k=2再见
⑴、解析式中自变量x的次数是___次,⑵、比例系数_____。1K≠0 2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。0,01,k 一条直线b一条直线4、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。一、三增大二、四减小5、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号:增大减小k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0<<><<>>>②①、②、③④③解:一次函数当x=1时,y=5。且它的图象与x轴交点
是(6,0)。由题意得解得∴一次函数的解析式为 y= - x+6。点评:用待定系数法求一次函数y=kx+b的解析式,可由已知条件给出的两对x、y的值,列出关于k、b的二元一次方程组。由此求出k、b的值,就可以得到所求的一次函数的解析式。例2、已知一次函数y=kx+b(k≠0)在x=1时,y=5,且
它的图象与x轴交点的横坐标是6,求这个一次函数的
解析式。 例3 柴油机在工作时油箱中的余油量Q(千克)
与工作时间t(小时)成一次函数关系,当工作开始时
油箱中有油40千克,工作3.5小时后,油箱中余油22.5
千克(1)写出余油量Q与时间t的函数关系式;(2)画出
这个函数的图象。解:(1)设Q=kt+b。把t=0,Q=40;t=3.5,Q=22.5
分别代入上式,得解得解析式为:Q=-5t+40 (0≤t≤8)(2)、取t=0,得Q=40;取t=8,得Q=0。描出点
A(0,40),B(8,0)。然后连成线段AB即是所
求的图形。点评:(1)求出函数关系式时,
必须找出自变量的取值范围。
(2)画函数图象时,应
根据函数自变量的取值范围来
确定图象的范围。20图象是包括
两端点的线段..AB2,00,1k=2再见
