一次函数的综合下学期]
图片预览



文档简介
课件14张PPT。一次函数的综合(一)回味练习:
1 函数y=2x-1与x轴交点坐标为_______ ,与y轴交点坐标为____,与两坐标轴围成的三角形面积是______.
2 若直线y=kx+b和直线y=-x平行,与y轴交点的纵坐标为-2,则直线的解析式为_______.
已知一次函数的图象经过点A(2,-1)
和点B,B是另一直线 与y轴的
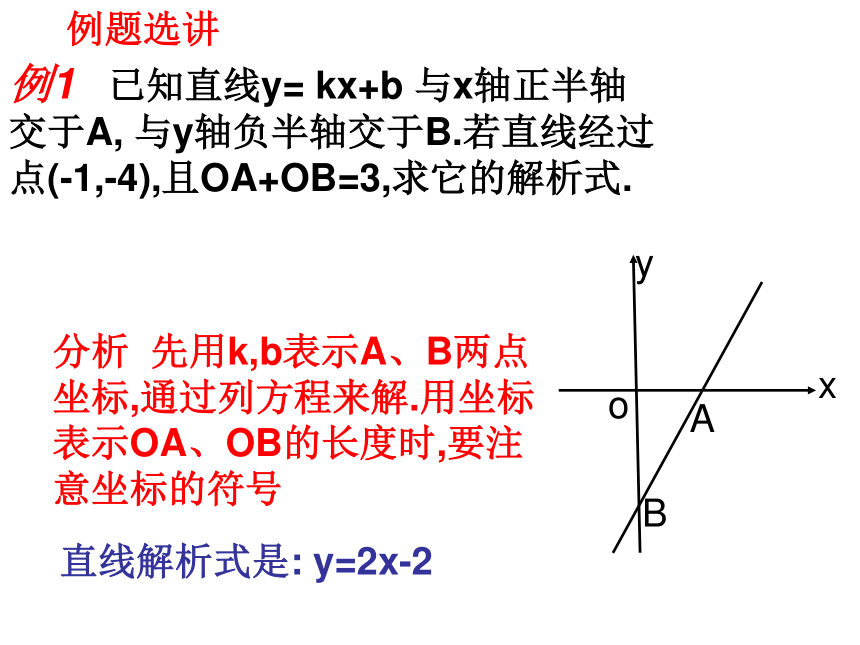
交点,这个一次函数的解析式___________.( ,0)(0,-1)例1 已知直线y= kx+b 与x轴正半轴交于A, 与y轴负半轴交于B.若直线经过点(-1,-4),且OA+OB=3,求它的解析式.
xyoAB直线解析式是: y=2x-2分析 先用k,b表示A、B两点坐标,通过列方程来解.用坐标表示OA、OB的长度时,要注意坐标的符号例题选讲
练习
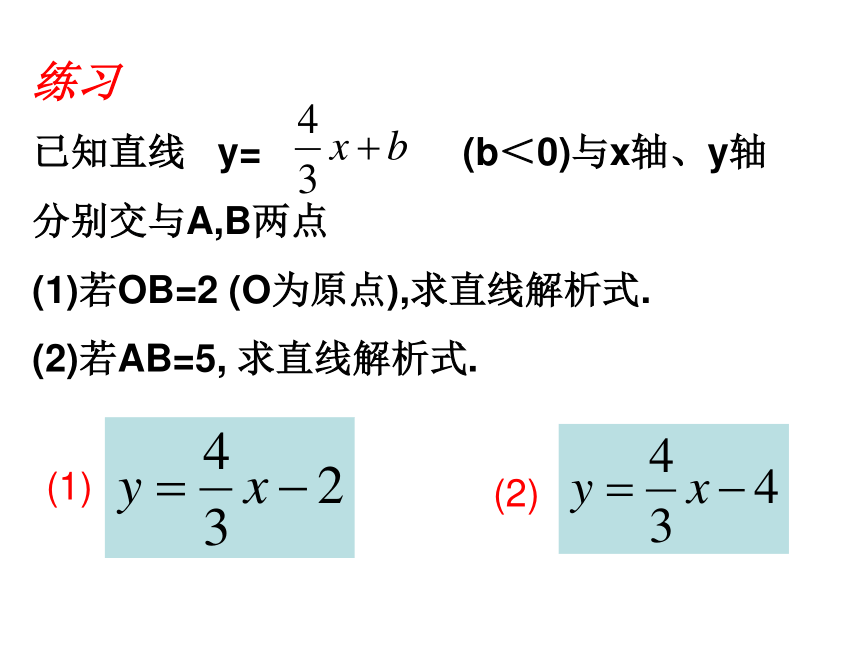
已知直线 y= (b<0)与x轴、y轴
分别交与A,B两点
(1)若OB=2 (O为原点),求直线解析式.
(2)若AB=5, 求直线解析式.(1)(2)例2 如图,△ABC的三个顶点分别在坐标轴上,边长BC=20,∠ABC=45°,∠BAC=15°.
(1)求A点的坐标;
(2)求经过A、C两点的直线解析式.xyABCoCAB已知:直线l的解析式为y=3x-6,求坐标原点O到直线L的距离。(0,-4)(6, )4(3,0)H例4、已知:点P是一次函数y=-2x+8的图象上一点,如果图象与x轴交于Q点,且△OPQ的面积等于6,求P点的坐标。y=-2x+8QP例5、若一次函数的图象交x轴于点A(-6,0),交正比例函数的图象于点B,且点B在第二象限,它的横坐标为- 4,又知:S△AOB=15,求直线AB的解析式。A(-6,0)(-4, ) By例6
已知直线l1:y=kx+2经过A、B两点,其中点A的坐标是( ,1),点B在y轴上.经过点A的直线l2与y轴交于点C,且与y轴的交角为30°.
求:(1)l1、l2的解析式.
(2)S△ABC(1)l1: l2: 或 例7 如图,以O为圆心,作半径为1的圆,AB是直径,和Y轴交与D、E两点, 过B的直线交圆于C,交Y轴正半轴于F,已知:S△ABC=3S△BOF。求直线BC解析式.x例8
如图,已知一次函数 的图象与x轴、
y轴分别交于A、B两点,点C、D都在X轴正半轴上,D点坐标为(2,0),若两钝角∠ABD=∠BCD.
(1)求证:BD2=DC·DA
(2)求直线BC的解析式.
(3)若P为直线BD上一点,
S△CDB=2S△CDP,
求点P的坐标.xyABODC(-3,0)(2,0)(0,1)例9 如图,直线 与x轴的
正半轴和y轴的正半轴交于点B,A两点,C点和P点都在第一象限,并且△ABC是等边三角形,△APD和△ABC的面积相等,求直线PC的解析式。
ABCP(0,1)( ,0)( ,2)思考题 如图:△ABC中, 点A、C在x轴正半轴上,点B在y轴正半轴上,且AB=AC.若此三角形腰长和腰上的高的长分别是关于x的方程x2-(2m-1)x+m2-5=0两个实数根,并且△ABC的面积等于10,求m值和经过B,C两点的直线解析式.oACByx(m=5 , )4553(0,4)(8,0)小结: 在求一次函数解析式时,一般有两个待定系数,因此,只要给出两个独立条件,就可求出它的解析式.当题目中出现角、长度等几何条件时,通常是把它转化为点的坐标后代入解析式,求出未知系数,得出函数解析式.
1 函数y=2x-1与x轴交点坐标为_______ ,与y轴交点坐标为____,与两坐标轴围成的三角形面积是______.
2 若直线y=kx+b和直线y=-x平行,与y轴交点的纵坐标为-2,则直线的解析式为_______.
已知一次函数的图象经过点A(2,-1)
和点B,B是另一直线 与y轴的
交点,这个一次函数的解析式___________.( ,0)(0,-1)例1 已知直线y= kx+b 与x轴正半轴交于A, 与y轴负半轴交于B.若直线经过点(-1,-4),且OA+OB=3,求它的解析式.
xyoAB直线解析式是: y=2x-2分析 先用k,b表示A、B两点坐标,通过列方程来解.用坐标表示OA、OB的长度时,要注意坐标的符号例题选讲
练习
已知直线 y= (b<0)与x轴、y轴
分别交与A,B两点
(1)若OB=2 (O为原点),求直线解析式.
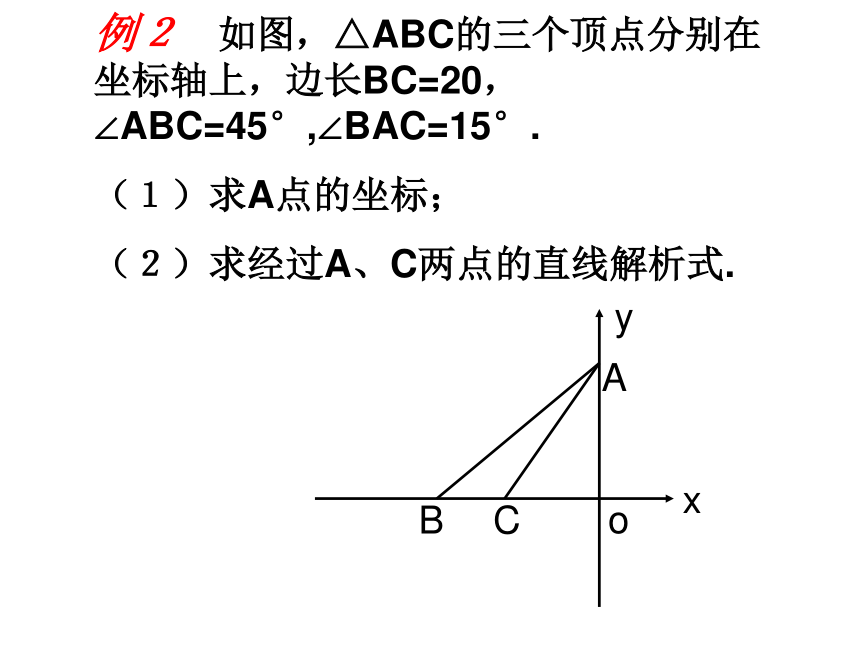
(2)若AB=5, 求直线解析式.(1)(2)例2 如图,△ABC的三个顶点分别在坐标轴上,边长BC=20,∠ABC=45°,∠BAC=15°.
(1)求A点的坐标;
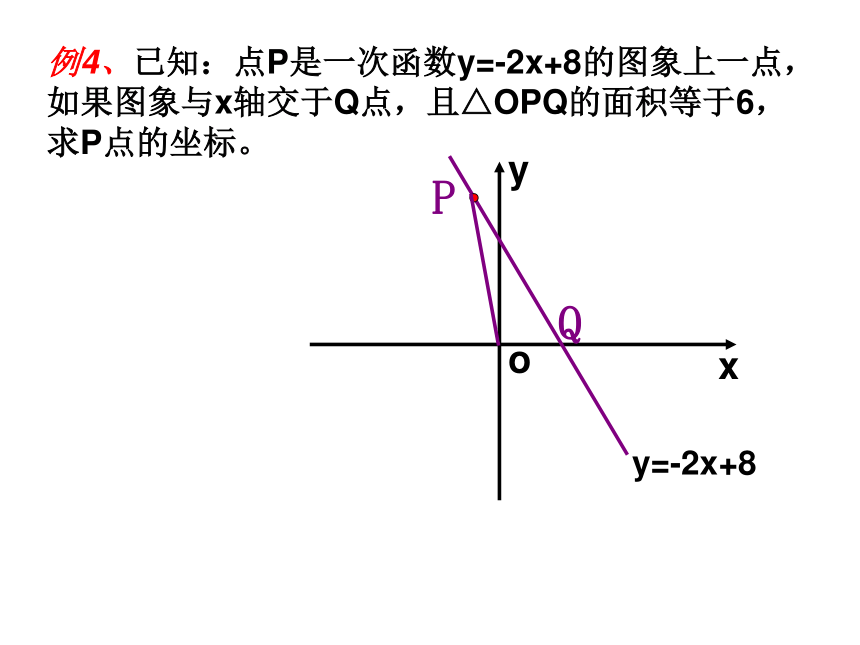
(2)求经过A、C两点的直线解析式.xyABCoCAB已知:直线l的解析式为y=3x-6,求坐标原点O到直线L的距离。(0,-4)(6, )4(3,0)H例4、已知:点P是一次函数y=-2x+8的图象上一点,如果图象与x轴交于Q点,且△OPQ的面积等于6,求P点的坐标。y=-2x+8QP例5、若一次函数的图象交x轴于点A(-6,0),交正比例函数的图象于点B,且点B在第二象限,它的横坐标为- 4,又知:S△AOB=15,求直线AB的解析式。A(-6,0)(-4, ) By例6
已知直线l1:y=kx+2经过A、B两点,其中点A的坐标是( ,1),点B在y轴上.经过点A的直线l2与y轴交于点C,且与y轴的交角为30°.
求:(1)l1、l2的解析式.
(2)S△ABC(1)l1: l2: 或 例7 如图,以O为圆心,作半径为1的圆,AB是直径,和Y轴交与D、E两点, 过B的直线交圆于C,交Y轴正半轴于F,已知:S△ABC=3S△BOF。求直线BC解析式.x例8
如图,已知一次函数 的图象与x轴、
y轴分别交于A、B两点,点C、D都在X轴正半轴上,D点坐标为(2,0),若两钝角∠ABD=∠BCD.
(1)求证:BD2=DC·DA
(2)求直线BC的解析式.
(3)若P为直线BD上一点,
S△CDB=2S△CDP,
求点P的坐标.xyABODC(-3,0)(2,0)(0,1)例9 如图,直线 与x轴的
正半轴和y轴的正半轴交于点B,A两点,C点和P点都在第一象限,并且△ABC是等边三角形,△APD和△ABC的面积相等,求直线PC的解析式。
ABCP(0,1)( ,0)( ,2)思考题 如图:△ABC中, 点A、C在x轴正半轴上,点B在y轴正半轴上,且AB=AC.若此三角形腰长和腰上的高的长分别是关于x的方程x2-(2m-1)x+m2-5=0两个实数根,并且△ABC的面积等于10,求m值和经过B,C两点的直线解析式.oACByx(m=5 , )4553(0,4)(8,0)小结: 在求一次函数解析式时,一般有两个待定系数,因此,只要给出两个独立条件,就可求出它的解析式.当题目中出现角、长度等几何条件时,通常是把它转化为点的坐标后代入解析式,求出未知系数,得出函数解析式.
