一次函数图象的应用[下学期]
图片预览





文档简介
课件14张PPT。 一次函数的图象和性质(应用)知识回顾:1、一次函数 与两数轴的交点坐标分别是:2、一次函数的图象是直线,两条直线两直线平行时:反之,也成立。两直线不平行时,求两直线交点坐标的方法是:解方程组4、一次函数 y=kx+b 的图象可以通过
把y=kx 的图象向上(下)平移 个单位得到.知识回顾:3、当 两个一次函数 ,b相等时,两直线交于同一点(0,b).
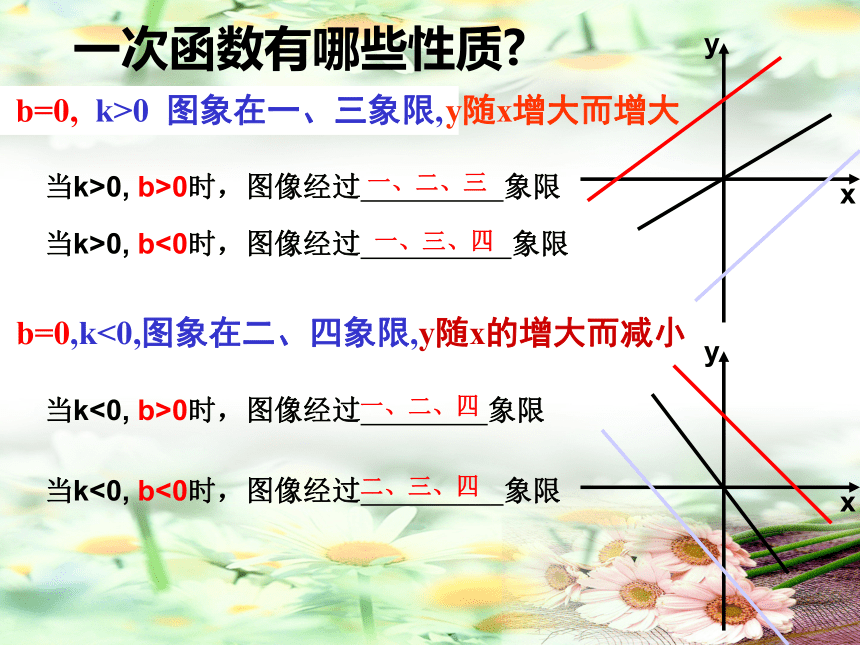
|b|b=0, k>0 图象在一、三象限, y随x增大而增大xyxyb=0,k<0,图象在二、四象限,y随x的增大而减小当k>0, b>0时,图像经过 象限当k>0, b<0时,图像经过 象限当k<0, b>0时,图像经过 象限当k<0, b<0时,图像经过 象限一、二、三一、三、四一、二、四二、三、四一次函数有哪些性质?1、已知一次函数下列四个
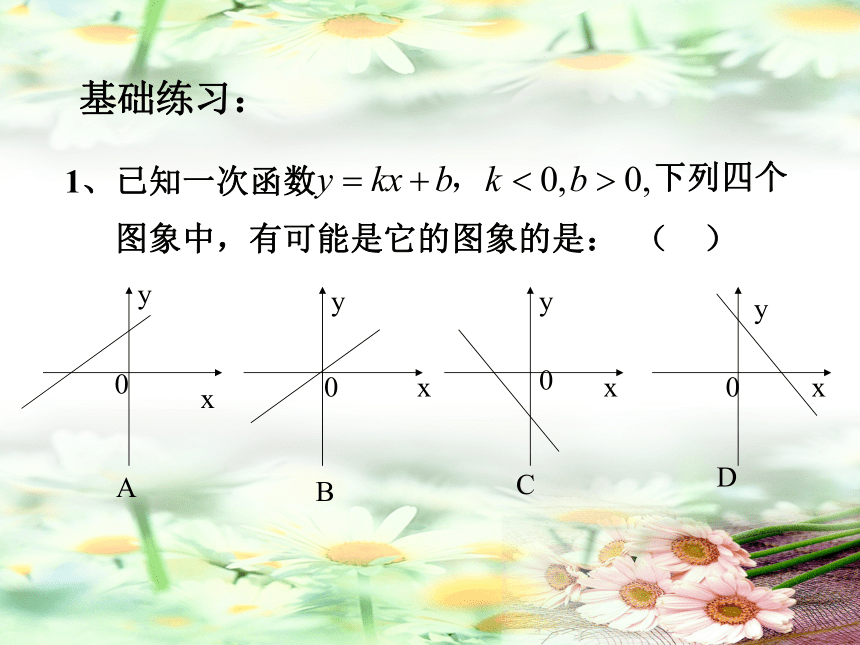
图象中,有可能是它的图象的是: ( )xxxxyyyy0000ABCD基础练习:2、已知一次函数y=(2m+4)x+(3-n),求:(1)m,n是什么数时,y随x的增大而增大?
(2) m,n是什么数时,函数图象与y轴的交点
在x轴的下方?
(3) m,n是什么数时,函数图象经过原点?
(4)若图象经过一、二、三象限,求m,n的取值范围。基础练习:3、已知直线y=x-5和y=2x-1,求它们的交点坐标. 基础练习:4、已知直线x-2y=-k-4和x+3y=4k+1,
若它们的交点在第一象限内,求k的取值范围; 例1、设直线 与x轴交点为A,与y轴交点为B, O为坐标原点,求△AOB的面积.一、面积问题:1、已知直线y=kx+b经过点(2,0),且与y轴的正半轴相交,此直线和坐标轴所围成三角形面积为6,求该直线的解析式。面积问题:2、已知一次函数y=kx+4的图像与两坐标轴围成的三角形的面积为16,求一次函数的解析式。面积问题:3、已知一次函数的图象交正比例函数图象于M点,交x轴于点N(-6,0)又知点M位于第二象限,其横坐标为-4,若△MON的面积为15,求正比例和一次函数解析式。C面积问题:例2、某医院研究所开发一种新药,在试验药效时发现,
如果成人按规定剂量服用,那么服药后2h血液中含药量
最高,达每毫升6微克,接着逐步衰减。每毫升血液中含
药量y(微克)随时间x(h)的变化如图所示,
(1)分别求出x≤2和x≥2时,与的函数关系式。
(2)如果每毫升血液中含药量为4微克或4微克以上时治疗
疾病是有效的,那么这个有效时间是多长?xy063210二、实际应用:实际应用:例2、在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时
剩余部分的高度y(cm)与燃烧时间x(h)之间的关系如图
所示。根据图回答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是多少?
(2)从点燃到燃尽所用的时间分别是多少?
(3)分别求出甲、乙两根蜡烛燃烧时y与x的函数关系式?
(4)燃烧多久时,甲、乙两根蜡烛的高度相等?12.53102530x(h)y(cm)甲乙2已知直线y=-x+2与x,y轴分别交于点A,B,另一直线
y=kx+b(k≠0)经过点C(1,0),且把三角形AOB分成两部分,(1)若三角形AOB被分成的两部分面积相等,求k和b;
(2)若三角形AOB被分成的两部分面积比为1:5,求k和b。聪明题
把y=kx 的图象向上(下)平移 个单位得到.知识回顾:3、当 两个一次函数 ,b相等时,两直线交于同一点(0,b).
|b|b=0, k>0 图象在一、三象限, y随x增大而增大xyxyb=0,k<0,图象在二、四象限,y随x的增大而减小当k>0, b>0时,图像经过 象限当k>0, b<0时,图像经过 象限当k<0, b>0时,图像经过 象限当k<0, b<0时,图像经过 象限一、二、三一、三、四一、二、四二、三、四一次函数有哪些性质?1、已知一次函数下列四个
图象中,有可能是它的图象的是: ( )xxxxyyyy0000ABCD基础练习:2、已知一次函数y=(2m+4)x+(3-n),求:(1)m,n是什么数时,y随x的增大而增大?
(2) m,n是什么数时,函数图象与y轴的交点
在x轴的下方?
(3) m,n是什么数时,函数图象经过原点?
(4)若图象经过一、二、三象限,求m,n的取值范围。基础练习:3、已知直线y=x-5和y=2x-1,求它们的交点坐标. 基础练习:4、已知直线x-2y=-k-4和x+3y=4k+1,
若它们的交点在第一象限内,求k的取值范围; 例1、设直线 与x轴交点为A,与y轴交点为B, O为坐标原点,求△AOB的面积.一、面积问题:1、已知直线y=kx+b经过点(2,0),且与y轴的正半轴相交,此直线和坐标轴所围成三角形面积为6,求该直线的解析式。面积问题:2、已知一次函数y=kx+4的图像与两坐标轴围成的三角形的面积为16,求一次函数的解析式。面积问题:3、已知一次函数的图象交正比例函数图象于M点,交x轴于点N(-6,0)又知点M位于第二象限,其横坐标为-4,若△MON的面积为15,求正比例和一次函数解析式。C面积问题:例2、某医院研究所开发一种新药,在试验药效时发现,
如果成人按规定剂量服用,那么服药后2h血液中含药量
最高,达每毫升6微克,接着逐步衰减。每毫升血液中含
药量y(微克)随时间x(h)的变化如图所示,
(1)分别求出x≤2和x≥2时,与的函数关系式。
(2)如果每毫升血液中含药量为4微克或4微克以上时治疗
疾病是有效的,那么这个有效时间是多长?xy063210二、实际应用:实际应用:例2、在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时
剩余部分的高度y(cm)与燃烧时间x(h)之间的关系如图
所示。根据图回答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是多少?
(2)从点燃到燃尽所用的时间分别是多少?
(3)分别求出甲、乙两根蜡烛燃烧时y与x的函数关系式?
(4)燃烧多久时,甲、乙两根蜡烛的高度相等?12.53102530x(h)y(cm)甲乙2已知直线y=-x+2与x,y轴分别交于点A,B,另一直线
y=kx+b(k≠0)经过点C(1,0),且把三角形AOB分成两部分,(1)若三角形AOB被分成的两部分面积相等,求k和b;
(2)若三角形AOB被分成的两部分面积比为1:5,求k和b。聪明题
