5.2.2同角三角函数的基本关系 课件(共31张PPT)
文档属性
| 名称 | 5.2.2同角三角函数的基本关系 课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 789.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-15 11:51:48 | ||
图片预览









文档简介
(共31张PPT)
5.2.2 同角三角函数的基本关系
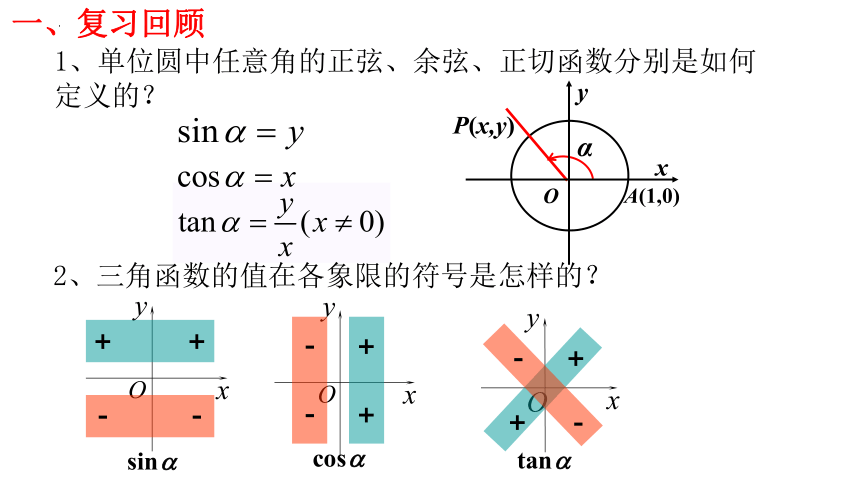
1、单位圆中任意角的正弦、余弦、正切函数分别是如何定义的?
P(x,y)
A(1,0)
x
y
α
O
一、复习回顾
2、三角函数的值在各象限的符号是怎样的?
x
y
O
+ +
- -
x
y
O
+
+
-
-
x
y
O
+
-
+
-
探究!上述诱导公式表明终边相同的角的同一三角函数值相等,那么,终边相同的角的三个三角函数值之间是否也有某种关系呢?
3、诱导公式一:
其中
一、复习回顾
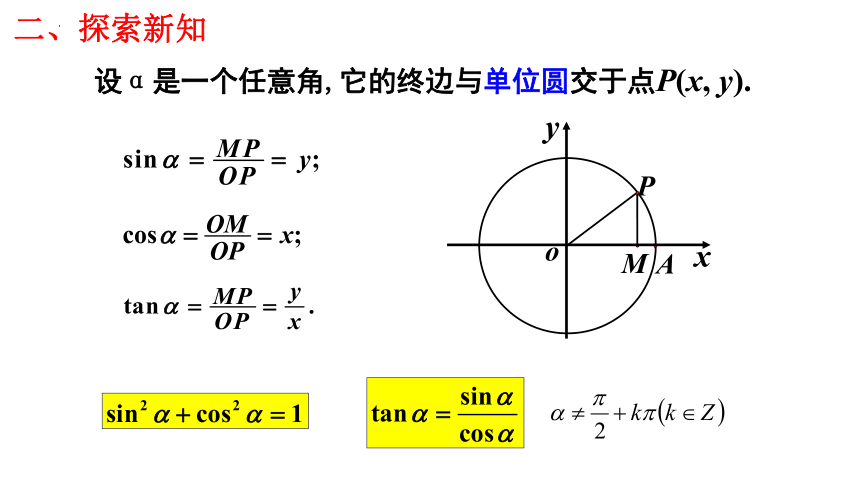
设α是一个任意角,它的终边与单位圆交于点P(x, y).
M
A
P
o
y
x
二、探索新知
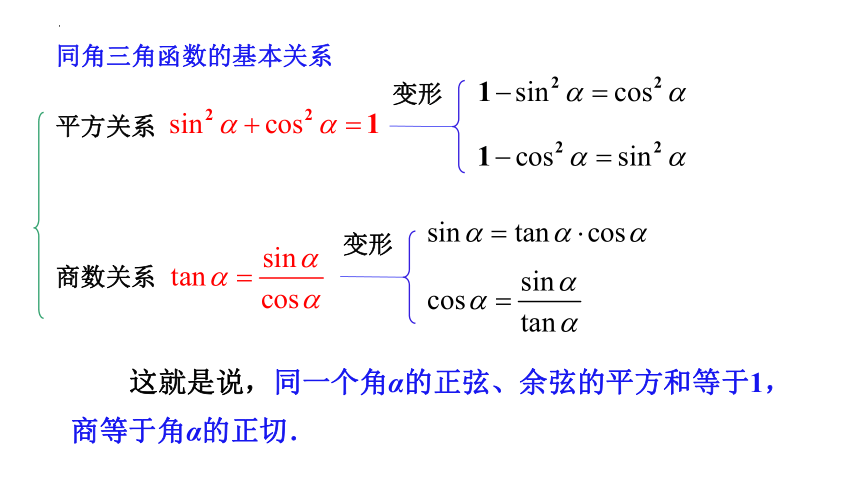
同角三角函数的基本关系
平方关系
商数关系
变形
变形
这就是说,同一个角α的正弦、余弦的平方和等于1,商等于角α的正切.
注意事项:
1. 公式中的角一定是同角,否则公式可能不成立. 如sin230 +cos260 ≠1.
2.同角不要拘泥于形式,关系式中的角可以是具体的度数,也可以是变量,也可以是代数式。比如 :
都是成立的
3. 在运用商数关系时,要注意等式成立的限制条件. 即cos α≠0. α≠kπ + ,k∈Z.
快速回答,判断对错
小试牛刀
不一定
类型一:利用同角三角函数的基本关系求值
解:∵tanα<0
∴α为第二或第四象限角
∴α为第二象限角时
当α为第四象限角时
类型一:利用同角三角函数的基本关系求值
步骤:
1.由已知三角函数的符号,确定其角终边所在的象限;
2.依据角终边所在象限进行分类讨论;
3.利用同角三角函数的基本关系式及其变形公式,求出其余三角函数值;
类型一:利用同角三角函数的基本关系求值
(1)若cosα= ,求tanα的值
(2)若tanα= ,求sinα的值
类型一:利用同角三角函数的基本关系求值
练习:
类型二:求关于sinα,cosα的齐次式的值(弦化切问题)
类型二:求关于sinα,cosα的齐次式的值(弦化切问题)
变式:
思路:
1.是一次齐次式,分子、分母同时除以cosα;
类型二:求关于sinα,cosα的齐次式的值(弦化切问题)
2.是二次齐次式,分子、分母同时除以cos2α;
3.是整式,先添加一个分母“1”并进行1的代换,然后分子、分母再同时除以cos2α;
类型二:求关于sinα,cosα的齐次式的值(弦化切问题)
练习:
已知 =2,计算下列各式的值
1)求的值
2)求 的值
3)求 的值
类型三:利用±
例3:
法一:
或
(舍)
类型三:利用±
例3:
法二:
类型三:利用±
例3:
法二:
类型三:利用±
例3:
法二:
类型三:利用±
思路点拨:
法1.直接联立方程组求值;
法2.利用完全平方公式, 将sinxcosx,sinx+cosx和sinx-cosx联系在一起,利用整体代换的思想求解
类型三:利用±
已知
1)求
2)求的值
3)求的值
练习:
类型四:同角三角函数的化简
例4:化简
类型四:同角三角函数的化简
例4:化简
类型四:同角三角函数的化简
思路点拨:
1.化异为同,通过切化弦减少函数种类;
2.对含有根号的,常把根号下的式子化成完全平方式,然后消去根号;
3.对于化简高次三角函数式,常利用 sin2α +cos2α=1进行降次。
类型五:同角三角函数的证明
例5:求证:
法一(作差法):
类型五:同角三角函数的证明
例5:求证:
法二(左推右):
除特殊注明外,我们假定三角函数恒等式都在两边有意义的情况下的恒等式
类型五:同角三角函数的证明
例5:求证:
法三(分析法):
类型五:同角三角函数的证明
例5:求证:
法1(两边凑):
类型五:同角三角函数的证明
例5:求证:
法2(右推左):
类型五:同角三角函数的证明
思路点拨:
法3.两边证:等式左右两边都比较复杂,证明左右两边等于同一个式子
法2.左推右或右推左:从一边开始,证他等于另一边
法1.作差法
课 堂 小 结
5.2.2 同角三角函数的基本关系
1、单位圆中任意角的正弦、余弦、正切函数分别是如何定义的?
P(x,y)
A(1,0)
x
y
α
O
一、复习回顾
2、三角函数的值在各象限的符号是怎样的?
x
y
O
+ +
- -
x
y
O
+
+
-
-
x
y
O
+
-
+
-
探究!上述诱导公式表明终边相同的角的同一三角函数值相等,那么,终边相同的角的三个三角函数值之间是否也有某种关系呢?
3、诱导公式一:
其中
一、复习回顾
设α是一个任意角,它的终边与单位圆交于点P(x, y).
M
A
P
o
y
x
二、探索新知
同角三角函数的基本关系
平方关系
商数关系
变形
变形
这就是说,同一个角α的正弦、余弦的平方和等于1,商等于角α的正切.
注意事项:
1. 公式中的角一定是同角,否则公式可能不成立. 如sin230 +cos260 ≠1.
2.同角不要拘泥于形式,关系式中的角可以是具体的度数,也可以是变量,也可以是代数式。比如 :
都是成立的
3. 在运用商数关系时,要注意等式成立的限制条件. 即cos α≠0. α≠kπ + ,k∈Z.
快速回答,判断对错
小试牛刀
不一定
类型一:利用同角三角函数的基本关系求值
解:∵tanα<0
∴α为第二或第四象限角
∴α为第二象限角时
当α为第四象限角时
类型一:利用同角三角函数的基本关系求值
步骤:
1.由已知三角函数的符号,确定其角终边所在的象限;
2.依据角终边所在象限进行分类讨论;
3.利用同角三角函数的基本关系式及其变形公式,求出其余三角函数值;
类型一:利用同角三角函数的基本关系求值
(1)若cosα= ,求tanα的值
(2)若tanα= ,求sinα的值
类型一:利用同角三角函数的基本关系求值
练习:
类型二:求关于sinα,cosα的齐次式的值(弦化切问题)
类型二:求关于sinα,cosα的齐次式的值(弦化切问题)
变式:
思路:
1.是一次齐次式,分子、分母同时除以cosα;
类型二:求关于sinα,cosα的齐次式的值(弦化切问题)
2.是二次齐次式,分子、分母同时除以cos2α;
3.是整式,先添加一个分母“1”并进行1的代换,然后分子、分母再同时除以cos2α;
类型二:求关于sinα,cosα的齐次式的值(弦化切问题)
练习:
已知 =2,计算下列各式的值
1)求的值
2)求 的值
3)求 的值
类型三:利用±
例3:
法一:
或
(舍)
类型三:利用±
例3:
法二:
类型三:利用±
例3:
法二:
类型三:利用±
例3:
法二:
类型三:利用±
思路点拨:
法1.直接联立方程组求值;
法2.利用完全平方公式, 将sinxcosx,sinx+cosx和sinx-cosx联系在一起,利用整体代换的思想求解
类型三:利用±
已知
1)求
2)求的值
3)求的值
练习:
类型四:同角三角函数的化简
例4:化简
类型四:同角三角函数的化简
例4:化简
类型四:同角三角函数的化简
思路点拨:
1.化异为同,通过切化弦减少函数种类;
2.对含有根号的,常把根号下的式子化成完全平方式,然后消去根号;
3.对于化简高次三角函数式,常利用 sin2α +cos2α=1进行降次。
类型五:同角三角函数的证明
例5:求证:
法一(作差法):
类型五:同角三角函数的证明
例5:求证:
法二(左推右):
除特殊注明外,我们假定三角函数恒等式都在两边有意义的情况下的恒等式
类型五:同角三角函数的证明
例5:求证:
法三(分析法):
类型五:同角三角函数的证明
例5:求证:
法1(两边凑):
类型五:同角三角函数的证明
例5:求证:
法2(右推左):
类型五:同角三角函数的证明
思路点拨:
法3.两边证:等式左右两边都比较复杂,证明左右两边等于同一个式子
法2.左推右或右推左:从一边开始,证他等于另一边
法1.作差法
课 堂 小 结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
