5.1.1任意角 课件(共28张PPT)
文档属性
| 名称 | 5.1.1任意角 课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 773.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-15 11:53:06 | ||
图片预览






文档简介
(共28张PPT)
5.1.1任意角
复习引入
什么是角?范围是多大?
定义:有公共端点的两射线组成的几何图形叫角.
顶点
边
边
角的范围:0°~360°
初中定义
新知探究
体操——李小鹏跳
2002年在匈牙利世锦赛上,李小鹏在跳马时做出的“踺子后手翻转体180度接直体前空翻转体900度”获得“李小鹏跳”命名.
新知探究
体操中有转体两周或转体两周半,如何度量这些角度呢?
新知探究
高中角的概念拓广以后,我们又有什么样的定义?
任意角的概念
1.角的概念:
角可以看成平面内 绕着它的 旋转所成的图形.
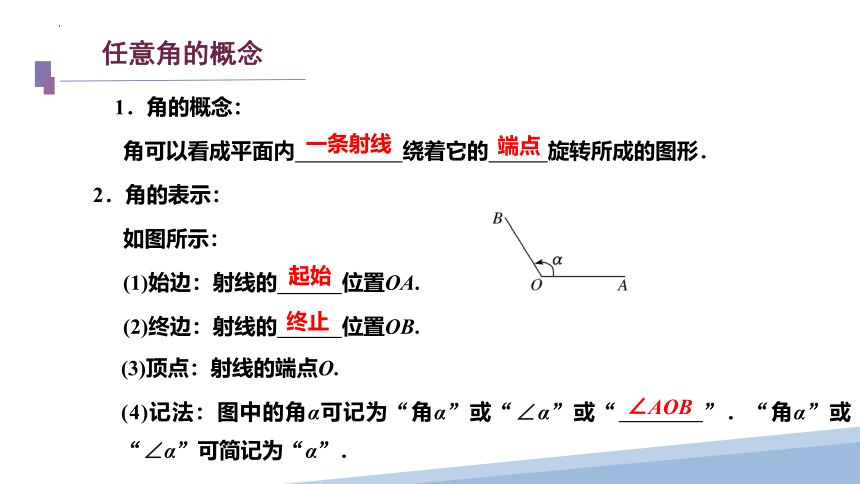
2.角的表示:
如图所示:
(1)始边:射线的 位置OA.
(2)终边:射线的 位置OB.
一条射线
端点
起始
终止
(3)顶点:射线的端点O.
(4)记法:图中的角α可记为“角α”或“∠α”或“ ”.“角α”或“∠α”可简记为“α”.
∠AOB
概念学习
3. 角的分类 :
名称 定义 图示
正角 一条射线绕其端点按________方向旋转形成的角
负角 一条射线绕其端点按________方向旋转形成的角
零角 一条射线_______做任何旋转形成的角
逆时针
顺时针
没有
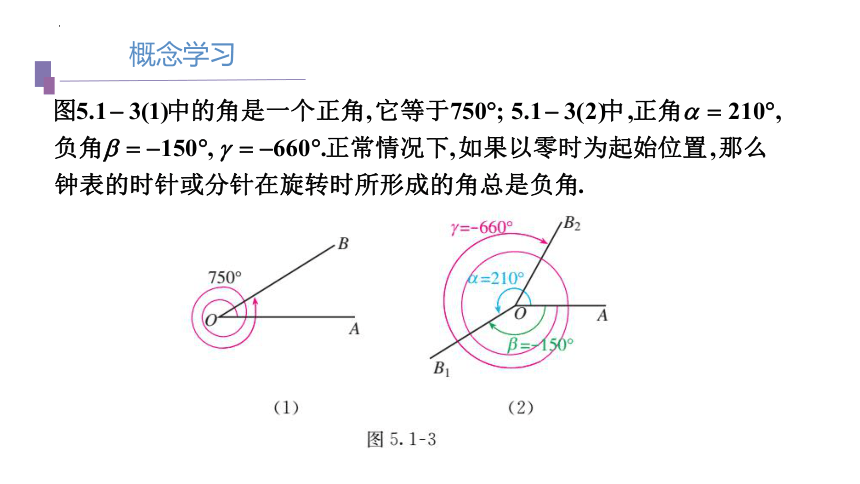
这样,我们就把角的概念推广到了任意角(any angle),包括正角、
负角和零角.
概念学习
概念学习
1.如何判断两个角相等?
2.如果旋转量相同,但旋转方向相反,则两个角之间是什么关系?
互为相反角
概念学习
3.角的加法、减法
练习
3.角的加法、减法
例:60°角的终边顺时针旋转120°,这时终边所对应的角为______;
60°角的终边逆时针旋转两周,这时终边所对应的角为______;
-60°
780°
-60°
60°-120°=-60°
60°+2×360°=780°
概念学习
我们通常在直角坐标系内讨论角.为了方便,使角的顶点与原点重合,角的始边与轴的非负半轴重合.那么,角的终边在第几象限,就说这个角是第几象限角.
如果角的终边落在坐标轴上,那么这个角不属于任何一个象限
轴线角
探究
将角按照上述方法放在直角坐标系中后,给定一个角,就有唯一的一条终边与之对应.反之,对于直角坐标系内任意一条射线OB(图5.1-6),以它为终边的角是否唯一?如果不唯一,那么终边相同的角有什么关系?
探究
1
都可以表示成-32°的角与k(k为整数)个周角的和
-32°=-30°+0×360°
所有与-32°终边相等的角:
探究
典例1
在0°~360°范围内,找出与-950°12′终边相同的角,并判断它是第几象限角
-950°12′+3×360°=129°48′
第二象限角
练习
在0°~360°范围内,找出与下列各角终边相同的角,并判断它是第几象限角
-54°18′+1×360°=305°42′
第四象限角
(1)-54°18′ (2)395°8′
395°8′+(-1)×360°=35°42′
第一象限角
典例2
写出终边在y轴上的角的集合
法一:(周角均分法)
∵y轴把周角(顶点为坐标原点)均分为两部分
∴终边落在y轴上的角的集合为
典例2
法二:(并集法)
在0°~360°范围内,终边在y轴上的角有两个,90°和270°,因此
所有与90°终边相同的角构成集合
所有与270°终边相同的角构成集合
于是终边在y轴上的角的集合为
典例3
例3 如图5-1-1所示.
(1)分别写出终边落在射线OA,OB上的角的集合;
(2)写出终边落在阴影部分(包括边界)的角的集合.
解:(1)终边落在射线OA上的角的集合为{α|α=90°+45°+k·360°,k∈Z}={α|α=135°+k·360°,k∈Z};
终边落在射线OB上的角的集合为{α|α=-30°+k·360°,k∈Z}.
(2)由题图可知,终边落在阴影部分(包括边界)的角的集合为
{α|-30°+k·360°≤α≤135°+k·360°,k∈Z}.
变式 如图5-1-2,分别写出终边落在阴影部分(包括边界)的角α的集合.
解:{α|45°+180°·k≤α≤90°+180°·k,k∈Z},{α|-150°+360°·k≤α≤120°+360°·k,k∈Z}.
图5-1-2
练习
[素养小结]
表示区域角的三个步骤
第一步:先按逆时针的方向找到区域的起始和终止边界.
第二步:按由小到大分别标出起始和终止边界对应的-360°~360°范围内的角α和β,写出最简区间{x|α第三步:将最简区间中的角α,β再加上360°的整数倍,即得区域角的集合.
课 中 探 究
例1 (1)(多选题)给出下列说法:①三角形的内角必是第一、二象限角;②终边与始边重合的角一定是零角;③将表的分针拨慢10分钟,则分针转过的角为60°;④小于90°的角是锐角.
其中错误的是 ( )
A.① B.② C.③ D.④
探究点一 任意角的概念与分类
ABD
课 中 探 究
(2)时间过了2小时30分,则分针转过的角度是 .
(3) 射线OA绕端点O顺时针旋转80°到OB位置,接着逆时针旋转250°到OC位置,然后再顺时针旋转270°到OD位置,则射线OA绕点O旋转到OD形成的角α= .
-900°
课 中 探 究
-100°
[素养小结]
(1)正确理解象限角与锐角、直角、钝角、平角、周角等概念,弄清角的始边与终边及旋转方向与大小.另外需要掌握判断结论正确与否的技巧,判断结论正确需要证明,而判断结论不正确只需举一个反例.
(2)要注意“旋转方向”决定角的“正负”,“旋转幅度”决定角的“绝对值大小”.
课 中 探 究
例2 (1)给出下列四个结论:①-75°角是第四象限角;②225°角是第三象限角;③540°角是第二象限角;④-315°角是第一象限角.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
探究点二 象限角和轴线角的理解及其应用
C
课 中 探 究
角度一 象限角、轴线角的判断
(2)[2022·山东沂水一中高一月考] 若α是第一象限角,则下列各角中是第四象限角的是 ( )
A.90°-α B.90°+α
C.360°-α D.180°+α
C
课 中 探 究
(3)终边与坐标轴重合的角α的集合是 ( )
A.{α|α=k·360°,k∈Z} B.{α|α=k·180°+90°,k∈Z}
C.{α|α=k·180°,k∈Z} D.{α|α=k·90°,k∈Z}
D
石泉县江南中学:子非鱼
谢谢观看
5.1.1任意角
复习引入
什么是角?范围是多大?
定义:有公共端点的两射线组成的几何图形叫角.
顶点
边
边
角的范围:0°~360°
初中定义
新知探究
体操——李小鹏跳
2002年在匈牙利世锦赛上,李小鹏在跳马时做出的“踺子后手翻转体180度接直体前空翻转体900度”获得“李小鹏跳”命名.
新知探究
体操中有转体两周或转体两周半,如何度量这些角度呢?
新知探究
高中角的概念拓广以后,我们又有什么样的定义?
任意角的概念
1.角的概念:
角可以看成平面内 绕着它的 旋转所成的图形.
2.角的表示:
如图所示:
(1)始边:射线的 位置OA.
(2)终边:射线的 位置OB.
一条射线
端点
起始
终止
(3)顶点:射线的端点O.
(4)记法:图中的角α可记为“角α”或“∠α”或“ ”.“角α”或“∠α”可简记为“α”.
∠AOB
概念学习
3. 角的分类 :
名称 定义 图示
正角 一条射线绕其端点按________方向旋转形成的角
负角 一条射线绕其端点按________方向旋转形成的角
零角 一条射线_______做任何旋转形成的角
逆时针
顺时针
没有
这样,我们就把角的概念推广到了任意角(any angle),包括正角、
负角和零角.
概念学习
概念学习
1.如何判断两个角相等?
2.如果旋转量相同,但旋转方向相反,则两个角之间是什么关系?
互为相反角
概念学习
3.角的加法、减法
练习
3.角的加法、减法
例:60°角的终边顺时针旋转120°,这时终边所对应的角为______;
60°角的终边逆时针旋转两周,这时终边所对应的角为______;
-60°
780°
-60°
60°-120°=-60°
60°+2×360°=780°
概念学习
我们通常在直角坐标系内讨论角.为了方便,使角的顶点与原点重合,角的始边与轴的非负半轴重合.那么,角的终边在第几象限,就说这个角是第几象限角.
如果角的终边落在坐标轴上,那么这个角不属于任何一个象限
轴线角
探究
将角按照上述方法放在直角坐标系中后,给定一个角,就有唯一的一条终边与之对应.反之,对于直角坐标系内任意一条射线OB(图5.1-6),以它为终边的角是否唯一?如果不唯一,那么终边相同的角有什么关系?
探究
1
都可以表示成-32°的角与k(k为整数)个周角的和
-32°=-30°+0×360°
所有与-32°终边相等的角:
探究
典例1
在0°~360°范围内,找出与-950°12′终边相同的角,并判断它是第几象限角
-950°12′+3×360°=129°48′
第二象限角
练习
在0°~360°范围内,找出与下列各角终边相同的角,并判断它是第几象限角
-54°18′+1×360°=305°42′
第四象限角
(1)-54°18′ (2)395°8′
395°8′+(-1)×360°=35°42′
第一象限角
典例2
写出终边在y轴上的角的集合
法一:(周角均分法)
∵y轴把周角(顶点为坐标原点)均分为两部分
∴终边落在y轴上的角的集合为
典例2
法二:(并集法)
在0°~360°范围内,终边在y轴上的角有两个,90°和270°,因此
所有与90°终边相同的角构成集合
所有与270°终边相同的角构成集合
于是终边在y轴上的角的集合为
典例3
例3 如图5-1-1所示.
(1)分别写出终边落在射线OA,OB上的角的集合;
(2)写出终边落在阴影部分(包括边界)的角的集合.
解:(1)终边落在射线OA上的角的集合为{α|α=90°+45°+k·360°,k∈Z}={α|α=135°+k·360°,k∈Z};
终边落在射线OB上的角的集合为{α|α=-30°+k·360°,k∈Z}.
(2)由题图可知,终边落在阴影部分(包括边界)的角的集合为
{α|-30°+k·360°≤α≤135°+k·360°,k∈Z}.
变式 如图5-1-2,分别写出终边落在阴影部分(包括边界)的角α的集合.
解:{α|45°+180°·k≤α≤90°+180°·k,k∈Z},{α|-150°+360°·k≤α≤120°+360°·k,k∈Z}.
图5-1-2
练习
[素养小结]
表示区域角的三个步骤
第一步:先按逆时针的方向找到区域的起始和终止边界.
第二步:按由小到大分别标出起始和终止边界对应的-360°~360°范围内的角α和β,写出最简区间{x|α
课 中 探 究
例1 (1)(多选题)给出下列说法:①三角形的内角必是第一、二象限角;②终边与始边重合的角一定是零角;③将表的分针拨慢10分钟,则分针转过的角为60°;④小于90°的角是锐角.
其中错误的是 ( )
A.① B.② C.③ D.④
探究点一 任意角的概念与分类
ABD
课 中 探 究
(2)时间过了2小时30分,则分针转过的角度是 .
(3) 射线OA绕端点O顺时针旋转80°到OB位置,接着逆时针旋转250°到OC位置,然后再顺时针旋转270°到OD位置,则射线OA绕点O旋转到OD形成的角α= .
-900°
课 中 探 究
-100°
[素养小结]
(1)正确理解象限角与锐角、直角、钝角、平角、周角等概念,弄清角的始边与终边及旋转方向与大小.另外需要掌握判断结论正确与否的技巧,判断结论正确需要证明,而判断结论不正确只需举一个反例.
(2)要注意“旋转方向”决定角的“正负”,“旋转幅度”决定角的“绝对值大小”.
课 中 探 究
例2 (1)给出下列四个结论:①-75°角是第四象限角;②225°角是第三象限角;③540°角是第二象限角;④-315°角是第一象限角.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
探究点二 象限角和轴线角的理解及其应用
C
课 中 探 究
角度一 象限角、轴线角的判断
(2)[2022·山东沂水一中高一月考] 若α是第一象限角,则下列各角中是第四象限角的是 ( )
A.90°-α B.90°+α
C.360°-α D.180°+α
C
课 中 探 究
(3)终边与坐标轴重合的角α的集合是 ( )
A.{α|α=k·360°,k∈Z} B.{α|α=k·180°+90°,k∈Z}
C.{α|α=k·180°,k∈Z} D.{α|α=k·90°,k∈Z}
D
石泉县江南中学:子非鱼
谢谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
