2.4.1圆的标准方程 课件(共30张PPT)
文档属性
| 名称 | 2.4.1圆的标准方程 课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-15 11:53:53 | ||
图片预览









文档简介
(共30张PPT)
2.4.1圆的标准方程
第二章 直线和圆的方程
月亮,是中国人心目中的宇宙精灵,古代人们在生活中崇拜、敬畏月亮,在文学作品中也大量描写、如果把天空看作一个平面,月亮当做一个圆,建立一个平面直角坐标系,那么圆的坐标方程如何表示
情境导学
《古朗月行》
唐 李白
小时不识月,
呼作白玉盘。
又疑瑶台镜,
飞在青云端。
思考1 圆是怎样定义的?确定它的要素又是什么呢?各要素与圆有怎样的关系?
探究新知
定义:平面内到定点的距离等于定长的点的集合叫作圆,
定点称为圆心(O),定长称为圆的半径(r).
确定圆的因素:圆心和半径
关系:圆心确定圆的位置,半径确定圆的大小.
O
r
A
M
r
x
O
y
探究新知
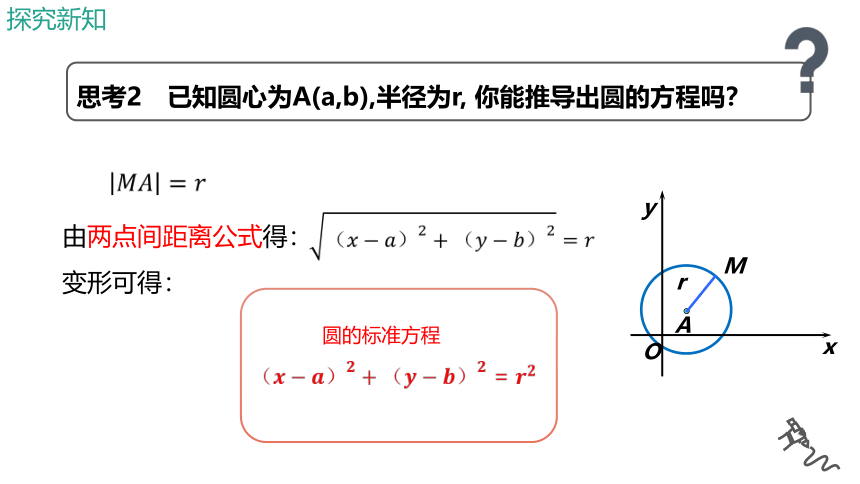
思考2 已知圆心为A(a,b),半径为r, 你能推导出圆的方程吗?
由两点间距离公式得:
变形可得:
圆的标准方程
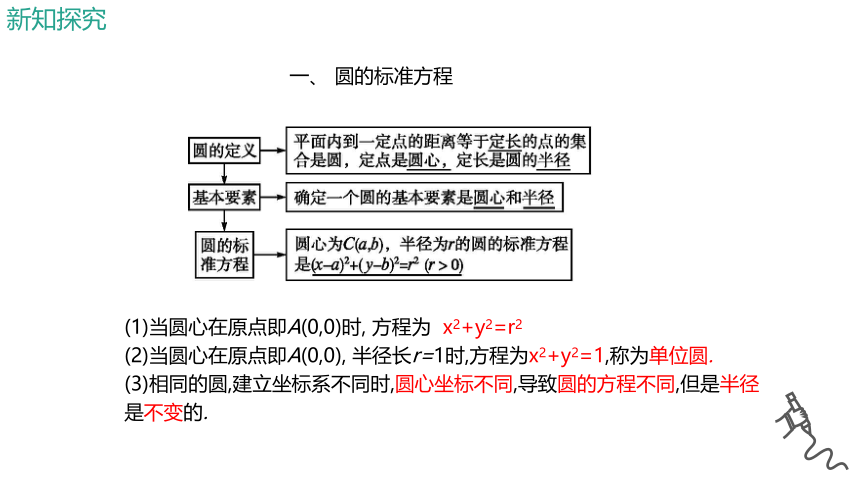
一、 圆的标准方程
(1)当圆心在原点即A(0,0)时, 方程为 x2+y2=r2
(2)当圆心在原点即A(0,0), 半径长r=1时,方程为x2+y2=1,称为单位圆.
(3)相同的圆,建立坐标系不同时,圆心坐标不同,导致圆的方程不同,但是半径是不变的.
新知探究
1.圆心在y轴上,半径为1,且过点(1,2)的圆的方程是( )
A.x2+(y-2)2=1 B.x2+(y+2)2=1
C.(x-1)2+(y-3)2=1 D.x2+(y-3)2=1
小试牛刀
解析:
设圆心为(0,b),则圆的方程为x2+(y-b)2=1,
又点(1,2)在圆上,所以1+(2-b)2=1,b=2,故方程为x2+(y-2)2=1.
答案:A
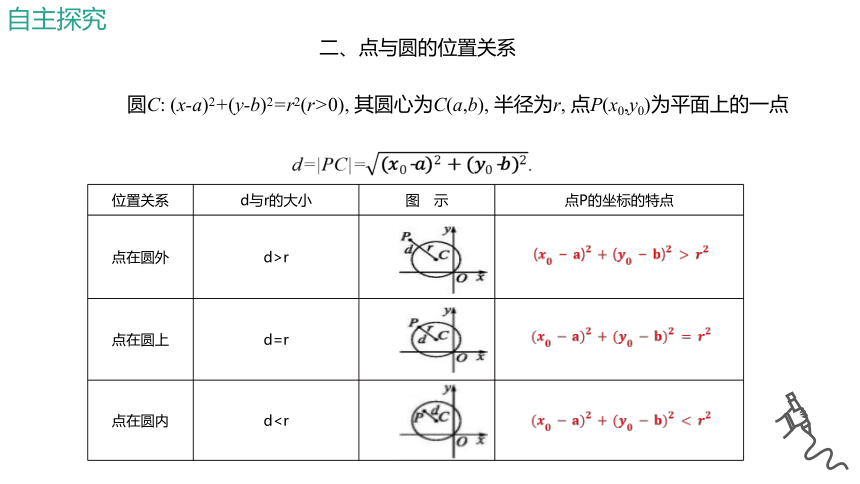
二、点与圆的位置关系
圆C: (x-a)2+(y-b)2=r2(r>0), 其圆心为C(a,b), 半径为r, 点P(x0,y0)为平面上的一点
位置关系 d与r的大小 图 示 点P的坐标的特点
点在圆外 d>r
点在圆上 d=r
点在圆内 d自主探究
小试牛刀
2.点P(-2,-2)和圆x2+y2=4的位置关系是( )
A.在圆上 B.在圆外
C.在圆内 D.以上都不对
解析:将点P的坐标代入圆的方程,则(-2)2+(-2)2=8>4,故点P在圆外.
答案:B
典例解析
例1.求圆心在直线x-2y-3=0上,且过点A(2,-3),B(-2,-5)的圆的标准方程.
思路分析:解答本题可以先根据所给条件确定圆心和半径,再写方程,也可以设出方程用待定系数法求解,也可以利用几何性质求出圆心和半径.
典例解析
例1.求圆心在直线x-2y-3=0上,且过点A(2,-3),B(-2,-5)的圆的标准方程.
解:(方法1)
设点C为圆心,
∵点C在直线:x-2y-3=0上,
∴可设点C的坐标为(2a+3,a).
又∵该圆经过A,B两点,∴|CA|=|CB|.
故所求圆的标准方程为(x+1)2+(y+2)2=10.
典例解析
例1.求圆心在直线x-2y-3=0上,且过点A(2,-3),B(-2,-5)的圆的标准方程.
解:(方法2)
设所求圆的标准方程为(x-a)2+(y-b)2=r2,圆心坐标为(a,b),
故所求圆的标准方程为(x+1)2+(y+2)2=10.
典例解析
例1.求圆心在直线x-2y-3=0上,且过点A(2,-3),B(-2,-5)的圆的标准方程.
归纳小结
圆的标准方程的两种求法
(1)几何法
它是利用图形的几何性质,如圆的性质等,直接求出圆的圆心和半径,代入圆的标准方程,从而得到圆的标准方程.
(2)待定系数法
由三个独立条件得到三个方程,解方程组以得到圆的标准方程中三个参数,从而确定圆的标准方程.它是求圆的方程最常用的方法,一般步骤是:
①设——设所求圆的方程为(x-a)2+(y-b)2=r2;
②列——由已知条件,建立关于a,b,r的方程组;
③解——解方程组,求出a,b,r;
④代——将a,b,r代入所设方程,得所求圆的方程.
跟踪训练
跟踪训练
跟踪训练2. 已知圆过点A(1,-2),B(-1,4),求:
(1)周长最小的圆的方程;
(2)圆心在直线2x-y-4=0上的圆的方程.
(1)解:当AB为直径时,过点A、B的圆的半径最小,从而周长最小,即
跟踪训练
跟踪训练2. 已知圆过点A(1,-2),B(-1,4),求:
(1)周长最小的圆的方程;
(2)圆心在直线2x-y-4=0上的圆的方程.
跟踪训练
跟踪训练3. 若点(1,1)在圆(x-a)2+(y+a)2=4的内部,则a的取值范围是( )
A.a<-1或a>1 B.-1解析:由题意可知,(1-a)2+(1+a)2<4,解得a2<1,
故-1答案:B
典题专栏
典题专栏
典题专栏
典题专栏
典题专栏
典题专栏
归纳小结
1.圆x2+y2=1的圆心到直线3x+4y-25=0的距离是( )
A.5 B.3 C.4 D.2
答案:A
达标检测
2.以C(2,-3)为圆心,且过点B(5,-1)的圆的方程为( )
A.(x-2)2+(y+3)2=25
B.(x+2)2+(y-3)2=65
C.(x+2)2+(y-3)2=53
D.(x-2)2+(y+3)2=13
答案:D
达标检测
3.已知点P(1,-1)在圆(x+2)2+y2=m的外部,则实数m的取值范围是 .
解析:由题意,得(1+2)2+(-1)2>m,即m<10.又m>0,故m的取值范围是(0,10).
答案:(0,10)
解析:已知圆的圆心(-2,0)关于原点的对称点为(2,0),半径不变,故所求对称圆的方程为(x-2)2+y2=5.
答案:(x-2)2+y2=5
4.圆(x+2)2+y2=5关于原点O(0,0)对称的圆的方程为 .
达标检测
达标检测
达标检测
点与圆的位置关系及其应用
点与圆的位置关系有三种:点在圆内、点在圆上、点在圆外.
判断点与圆的位置关系有两种方法:一是用圆心到该点的距离与半径比较,二是代入圆的标准方程,判断与r2的大小关系.通过点与圆的位置关系建立方程或不等式可求参数值或参数的取值范围.
课堂总结
2.4.1圆的标准方程
第二章 直线和圆的方程
月亮,是中国人心目中的宇宙精灵,古代人们在生活中崇拜、敬畏月亮,在文学作品中也大量描写、如果把天空看作一个平面,月亮当做一个圆,建立一个平面直角坐标系,那么圆的坐标方程如何表示
情境导学
《古朗月行》
唐 李白
小时不识月,
呼作白玉盘。
又疑瑶台镜,
飞在青云端。
思考1 圆是怎样定义的?确定它的要素又是什么呢?各要素与圆有怎样的关系?
探究新知
定义:平面内到定点的距离等于定长的点的集合叫作圆,
定点称为圆心(O),定长称为圆的半径(r).
确定圆的因素:圆心和半径
关系:圆心确定圆的位置,半径确定圆的大小.
O
r
A
M
r
x
O
y
探究新知
思考2 已知圆心为A(a,b),半径为r, 你能推导出圆的方程吗?
由两点间距离公式得:
变形可得:
圆的标准方程
一、 圆的标准方程
(1)当圆心在原点即A(0,0)时, 方程为 x2+y2=r2
(2)当圆心在原点即A(0,0), 半径长r=1时,方程为x2+y2=1,称为单位圆.
(3)相同的圆,建立坐标系不同时,圆心坐标不同,导致圆的方程不同,但是半径是不变的.
新知探究
1.圆心在y轴上,半径为1,且过点(1,2)的圆的方程是( )
A.x2+(y-2)2=1 B.x2+(y+2)2=1
C.(x-1)2+(y-3)2=1 D.x2+(y-3)2=1
小试牛刀
解析:
设圆心为(0,b),则圆的方程为x2+(y-b)2=1,
又点(1,2)在圆上,所以1+(2-b)2=1,b=2,故方程为x2+(y-2)2=1.
答案:A
二、点与圆的位置关系
圆C: (x-a)2+(y-b)2=r2(r>0), 其圆心为C(a,b), 半径为r, 点P(x0,y0)为平面上的一点
位置关系 d与r的大小 图 示 点P的坐标的特点
点在圆外 d>r
点在圆上 d=r
点在圆内 d
小试牛刀
2.点P(-2,-2)和圆x2+y2=4的位置关系是( )
A.在圆上 B.在圆外
C.在圆内 D.以上都不对
解析:将点P的坐标代入圆的方程,则(-2)2+(-2)2=8>4,故点P在圆外.
答案:B
典例解析
例1.求圆心在直线x-2y-3=0上,且过点A(2,-3),B(-2,-5)的圆的标准方程.
思路分析:解答本题可以先根据所给条件确定圆心和半径,再写方程,也可以设出方程用待定系数法求解,也可以利用几何性质求出圆心和半径.
典例解析
例1.求圆心在直线x-2y-3=0上,且过点A(2,-3),B(-2,-5)的圆的标准方程.
解:(方法1)
设点C为圆心,
∵点C在直线:x-2y-3=0上,
∴可设点C的坐标为(2a+3,a).
又∵该圆经过A,B两点,∴|CA|=|CB|.
故所求圆的标准方程为(x+1)2+(y+2)2=10.
典例解析
例1.求圆心在直线x-2y-3=0上,且过点A(2,-3),B(-2,-5)的圆的标准方程.
解:(方法2)
设所求圆的标准方程为(x-a)2+(y-b)2=r2,圆心坐标为(a,b),
故所求圆的标准方程为(x+1)2+(y+2)2=10.
典例解析
例1.求圆心在直线x-2y-3=0上,且过点A(2,-3),B(-2,-5)的圆的标准方程.
归纳小结
圆的标准方程的两种求法
(1)几何法
它是利用图形的几何性质,如圆的性质等,直接求出圆的圆心和半径,代入圆的标准方程,从而得到圆的标准方程.
(2)待定系数法
由三个独立条件得到三个方程,解方程组以得到圆的标准方程中三个参数,从而确定圆的标准方程.它是求圆的方程最常用的方法,一般步骤是:
①设——设所求圆的方程为(x-a)2+(y-b)2=r2;
②列——由已知条件,建立关于a,b,r的方程组;
③解——解方程组,求出a,b,r;
④代——将a,b,r代入所设方程,得所求圆的方程.
跟踪训练
跟踪训练
跟踪训练2. 已知圆过点A(1,-2),B(-1,4),求:
(1)周长最小的圆的方程;
(2)圆心在直线2x-y-4=0上的圆的方程.
(1)解:当AB为直径时,过点A、B的圆的半径最小,从而周长最小,即
跟踪训练
跟踪训练2. 已知圆过点A(1,-2),B(-1,4),求:
(1)周长最小的圆的方程;
(2)圆心在直线2x-y-4=0上的圆的方程.
跟踪训练
跟踪训练3. 若点(1,1)在圆(x-a)2+(y+a)2=4的内部,则a的取值范围是( )
A.a<-1或a>1 B.-1
故-1
典题专栏
典题专栏
典题专栏
典题专栏
典题专栏
典题专栏
归纳小结
1.圆x2+y2=1的圆心到直线3x+4y-25=0的距离是( )
A.5 B.3 C.4 D.2
答案:A
达标检测
2.以C(2,-3)为圆心,且过点B(5,-1)的圆的方程为( )
A.(x-2)2+(y+3)2=25
B.(x+2)2+(y-3)2=65
C.(x+2)2+(y-3)2=53
D.(x-2)2+(y+3)2=13
答案:D
达标检测
3.已知点P(1,-1)在圆(x+2)2+y2=m的外部,则实数m的取值范围是 .
解析:由题意,得(1+2)2+(-1)2>m,即m<10.又m>0,故m的取值范围是(0,10).
答案:(0,10)
解析:已知圆的圆心(-2,0)关于原点的对称点为(2,0),半径不变,故所求对称圆的方程为(x-2)2+y2=5.
答案:(x-2)2+y2=5
4.圆(x+2)2+y2=5关于原点O(0,0)对称的圆的方程为 .
达标检测
达标检测
达标检测
点与圆的位置关系及其应用
点与圆的位置关系有三种:点在圆内、点在圆上、点在圆外.
判断点与圆的位置关系有两种方法:一是用圆心到该点的距离与半径比较,二是代入圆的标准方程,判断与r2的大小关系.通过点与圆的位置关系建立方程或不等式可求参数值或参数的取值范围.
课堂总结
