12.1 算术平方根(2)[上学期]
文档属性
| 名称 | 12.1 算术平方根(2)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 131.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-21 00:00:00 | ||
图片预览











文档简介
课件30张PPT。 算术平方根3、若x2=25,则x=____,若x2=2.25,则负数x=____.2、4的平方根是____,4是___的平方根.
一、复习巩固:
1、如果________,那么___是___的平方根.
x2=axa±216±5-1.5
二、新知探究:
1、1的正的平方根为_____,
2的正的平方根为_____,
3的正的平方根为_____,
4的正的平方根为_____,
正数a的正的平方根为_____.
我们把正数a的正的平方根叫做a的算术平方根。
零的平方根也叫做零的算术平方根。
正数a的算术平方根记作:
它的另一个平方根是它的相反数,记作:
因此一个正数a的平方根表示为:0的平方根还是0那么求一个正数的平方根,只要求出它的算术平方根后,就可以写出它的平方根了。 36的算术平方根记作 ,平方根记作 ,
36的算术平方根是 ,平方根是 ,7的算术平方根记作 ,平方根记作 ,★ 一个正数有 个平方根,它们互
为 。一个正数有 个
算术平方根求下列各数的算术平方根:
(1)100 (2) (3)0.0001解:(1)因为 =100,所以100的算术平方根为10,即 =10。(2)因为 = ,所以 的算
术平方根是 即 =
求下列各数的算术平方根:
81 9 0 (-2)2 3-2解:(1)∵92=81
∴81的算术平方根是9
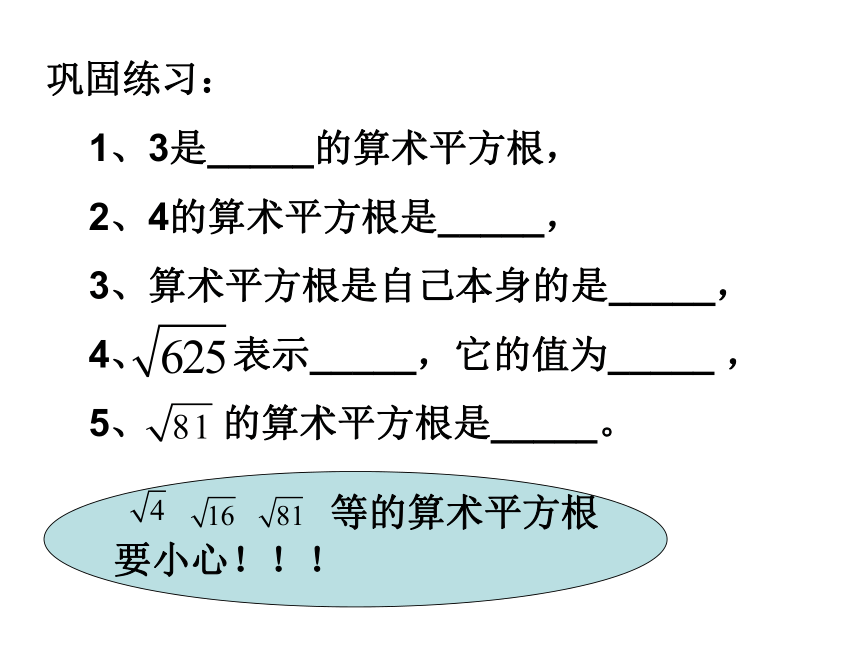
即以下请同学们自己解答求出下列各式的算术平方根.你会做吗?(4) 0.0025(5) 121(6) 32(7) 试一试求下列各式的值:⑴⑵⑶⑷巩固练习:
1、3是_____的算术平方根,
2、4的算术平方根是_____,
3、算术平方根是自己本身的是_____,
4、 表示_____,它的值为_____ ,
5、 的算术平方根是_____。等的算术平方根要小心!!! 并不是所有的正数我们都可以口算得出它的平方根的,如:5的平方根,8的平方根等怎么来计算它们的结果呢?我们要用到计数器来运算结果.例4:用计数器求下列各数的算术平方根:
(1) 529 (2) 1225 (3) 5 (4)44.81试一试:请尝试完成书本第5页练习第2、3题拓展思维:2、若一个正数的平方根为a+5和a+1,求a的值和这个正数。
3、若 有算术平方根,求x。1、求 和 的平方根和算术平方根。
2、说出下列各数开平方的结果。
(1)49 (2)1.69 (3)529 (4)44.81练一练:3、用计算器求下列各数的算术平方根(1) 529; (2)1225; (3)44.814.求x的值判断下列说法是否正确.1. 的平方根是±16. ( ) 2. 一定是正数. ( ) 3.a2的算术平方根是a. ( )4.若 , 则a=-5. ( )5. ( )6.-6是(-6)2的平方根. ( ) 7.若x2=36,则x= ( ) ×××××√√例1. 已知 有意义,则x一定是 ( )
A.正数 B. 负数
C. 非负数 D. 非正数例2.求下列各式的值D解:(1)原式=25(2)原式=(3)原式=要使式子有意义,必须满足: 解:所以,x 的取值范围是.(4)、正数a的正的平方根为_____,负的平方根是________. (3)、如果正数m满足9m2-16=0,那么3m+5的负的平方根是________.
(2)、式子 中x的取值范围是________.(1)、式子 中x的取值范围是________.解:根据非负数 的性质得:已知,(4x-4y+1)2+ + =0
求x-y+z的平方根。解:由题意,得4x-4y+1=02y+z=0
=0z-解得x-y+z=∴∴
(1)(-5)2的平方根是 ,算术平方根 是 ;±55±22±3(4)若(x-1)2=2,则x= ,练习:(5)若一个数的一个平方根为-7,则另一个平方根为 ,这个数是 。749(6)若一个正数的两个平方根为2a-6、3a+1,则a= ,这个正数为 ;116(7)平方根等于本身的数是 ,
算术平方根等于它本身的数是 ,算术平方根和平方根相等的数是 ;00、10D0202005
再练习课堂小结2、平方根与算术平方根的求法。3、非负数的性质的简单的运用。1、平方根与算术平方根区别。如果一个正数的算术平方根为m,则比这个数大2的数的算术平方根是多少?跟我练 (1)要做一个面积为2平方米的正方形桌面,它的边长为多少? (2)某展览馆要布置一个50平方米的正方形展厅,问展厅的边长为多少?
应用(3)小刚同学的房间地板面积为16平方米,恰好由64块正方形的地板砖铺成,求每块地板砖的边长是多少?应 用(-0.01)2=--------------2 =--------------2 =--------------探索 & 交流-a若 有意义,那么a的范围是--------- a若 有意义,那么a的范围是--------- 5( )2=--------------a( )2=--------------0.015a2=--------------2 =--------------(-5)结论
一、复习巩固:
1、如果________,那么___是___的平方根.
x2=axa±216±5-1.5
二、新知探究:
1、1的正的平方根为_____,
2的正的平方根为_____,
3的正的平方根为_____,
4的正的平方根为_____,
正数a的正的平方根为_____.
我们把正数a的正的平方根叫做a的算术平方根。
零的平方根也叫做零的算术平方根。
正数a的算术平方根记作:
它的另一个平方根是它的相反数,记作:
因此一个正数a的平方根表示为:0的平方根还是0那么求一个正数的平方根,只要求出它的算术平方根后,就可以写出它的平方根了。 36的算术平方根记作 ,平方根记作 ,
36的算术平方根是 ,平方根是 ,7的算术平方根记作 ,平方根记作 ,★ 一个正数有 个平方根,它们互
为 。一个正数有 个
算术平方根求下列各数的算术平方根:
(1)100 (2) (3)0.0001解:(1)因为 =100,所以100的算术平方根为10,即 =10。(2)因为 = ,所以 的算
术平方根是 即 =
求下列各数的算术平方根:
81 9 0 (-2)2 3-2解:(1)∵92=81
∴81的算术平方根是9
即以下请同学们自己解答求出下列各式的算术平方根.你会做吗?(4) 0.0025(5) 121(6) 32(7) 试一试求下列各式的值:⑴⑵⑶⑷巩固练习:
1、3是_____的算术平方根,
2、4的算术平方根是_____,
3、算术平方根是自己本身的是_____,
4、 表示_____,它的值为_____ ,
5、 的算术平方根是_____。等的算术平方根要小心!!! 并不是所有的正数我们都可以口算得出它的平方根的,如:5的平方根,8的平方根等怎么来计算它们的结果呢?我们要用到计数器来运算结果.例4:用计数器求下列各数的算术平方根:
(1) 529 (2) 1225 (3) 5 (4)44.81试一试:请尝试完成书本第5页练习第2、3题拓展思维:2、若一个正数的平方根为a+5和a+1,求a的值和这个正数。
3、若 有算术平方根,求x。1、求 和 的平方根和算术平方根。
2、说出下列各数开平方的结果。
(1)49 (2)1.69 (3)529 (4)44.81练一练:3、用计算器求下列各数的算术平方根(1) 529; (2)1225; (3)44.814.求x的值判断下列说法是否正确.1. 的平方根是±16. ( ) 2. 一定是正数. ( ) 3.a2的算术平方根是a. ( )4.若 , 则a=-5. ( )5. ( )6.-6是(-6)2的平方根. ( ) 7.若x2=36,则x= ( ) ×××××√√例1. 已知 有意义,则x一定是 ( )
A.正数 B. 负数
C. 非负数 D. 非正数例2.求下列各式的值D解:(1)原式=25(2)原式=(3)原式=要使式子有意义,必须满足: 解:所以,x 的取值范围是.(4)、正数a的正的平方根为_____,负的平方根是________. (3)、如果正数m满足9m2-16=0,那么3m+5的负的平方根是________.
(2)、式子 中x的取值范围是________.(1)、式子 中x的取值范围是________.解:根据非负数 的性质得:已知,(4x-4y+1)2+ + =0
求x-y+z的平方根。解:由题意,得4x-4y+1=02y+z=0
=0z-解得x-y+z=∴∴
(1)(-5)2的平方根是 ,算术平方根 是 ;±55±22±3(4)若(x-1)2=2,则x= ,练习:(5)若一个数的一个平方根为-7,则另一个平方根为 ,这个数是 。749(6)若一个正数的两个平方根为2a-6、3a+1,则a= ,这个正数为 ;116(7)平方根等于本身的数是 ,
算术平方根等于它本身的数是 ,算术平方根和平方根相等的数是 ;00、10D0202005
再练习课堂小结2、平方根与算术平方根的求法。3、非负数的性质的简单的运用。1、平方根与算术平方根区别。如果一个正数的算术平方根为m,则比这个数大2的数的算术平方根是多少?跟我练 (1)要做一个面积为2平方米的正方形桌面,它的边长为多少? (2)某展览馆要布置一个50平方米的正方形展厅,问展厅的边长为多少?
应用(3)小刚同学的房间地板面积为16平方米,恰好由64块正方形的地板砖铺成,求每块地板砖的边长是多少?应 用(-0.01)2=--------------2 =--------------2 =--------------探索 & 交流-a若 有意义,那么a的范围是--------- a若 有意义,那么a的范围是--------- 5( )2=--------------a( )2=--------------0.015a2=--------------2 =--------------(-5)结论
