12.1 平方根[上学期]
图片预览








文档简介
课件21张PPT。 第16章 数的开方
16.1.1 平方根(1) 授课教师: 梁文昌
第一周第一节八年级数学(下) 华师版教材南头初级中学初二级数学备课组一、教学目标1、掌握平方根及算术平方根的概念。
2、能够通过平方运算求一个非负数的平方根及算术平方根。
3、培养学生观察能力和概括问题的力。二、重点:平方根和算术平方根的 概念和性质。三、难点:平方根与算术平方根的
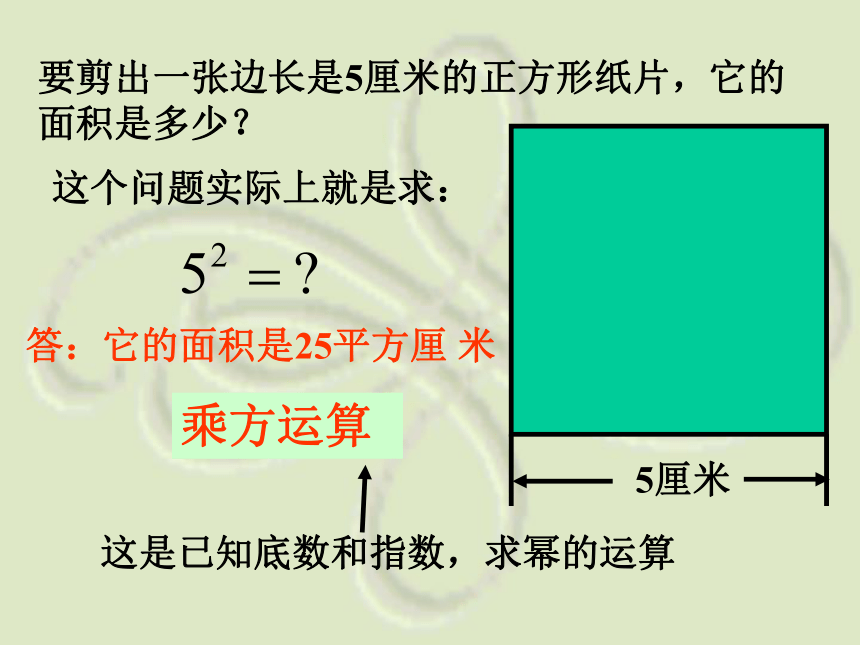
区别与联系。我们已学过了有理数的加法、减法、乘法、除法、乘方这五种运算。在这五种运算中那些是逆运算呢?★加法与减法互为逆运算;★乘法与除法互为逆运算;★那么乘方与谁互为逆运算呢?回忆与思考:我们先来复习乘方的有关内容:底数幂指数要剪出一张边长是5厘米的正方形纸片,它的面积是多少?这个问题实际上就是求:答:它的面积是25平方厘 米这是已知底数和指数,求幂的运算乘方运算我们把问题反过来,要做一张面积是25平方厘米的方桌面,它的边长是多少厘米? 实际上就是要求出一个数,使它的平方等于25,即:显然,括号里应是±5,但-5不符题意。∴方桌面的边长应是5厘米。25平方厘米认真观察下式可知:这是已知指数和幂求底数的运算,叫做开方运算。我们把括号里的±5叫做25的平方根(二次方根)。例如:∴3 和 -3 都是9的平方根。又例如:∴ 0.4 和 -0.4 都是0.16的平方根。 即0.16的平方根有两个,一个是+0.4;另一个是-0.4。 一个正数有两个平方根,这两个平方根互为相反数。∴ 零的平方根是零。这两个平方根互为相反数。∵任何数的平方都不可能是负数∴负数没有平方根通过上面的学习可以得到平方根的性质:★一个正数有两个平方根,它们互为相反数。★零的平方根是零。★负数没有平方根。 例1:判断下列各数有没有平方根,如果有平方根,试求出它的平方根;如果没有平方根,说明理由。我们来试一试,请看书中第2页试一试及课后练习1有,81的平方根是±9没有,因为负数没有平方根有,0的平方根是0有,49的平方根是±7没有,因为负数没有平方根想一想 “负数没有平方根”与“一个正数的平方根不能为负数”这两种说法正确吗? 求一个数的平方根(二次方根)的运算,叫做开平方,开平方运算的结果就是平方根。 根据乘方和开方的意义,我们已知道:乘方和开方运算互为逆运算。平方和开平方互为逆运算。求平方根的写法如下:
正数x的两个平方根可分别写作
(正号一般省略),我们可以合并成为
读作:正负根号x 例2:求下列各数的平方根。解: 我们可以这样考虑∴100的平方根是±10请你妨照上面的例子完成其余三个小题。我们定义正数a的正的平方根,叫做a的算术平方根.例如:100的算术平方根为10,记作 例3:求下列各数的算术平方根。
(1)144 (2)49 (3)2.25
0的算术平方根是多少呢?负数有算术平方根吗?算术平方根和平方根的关系是怎样的?问题:拓展思维:2、若一个正数的平方根为a+5和a+1,求a的值和这个正数。
1、求 和 的平方根和算术平方根。小结:这节课我们学到了哪些知识(1)如果一个数的平方等于a,这个数叫做a的平方根;
(2)正数a的平方根有两个,它们互为相反数,零的平方根是零,负数没有平方根;
(3)求一个数的平方根的运算叫做开平方,平方和开平方互为逆运算.作业 P7习题16.1 第1题课堂小测1、说出121、144、169、225、256、289、324、361的平方根。
2、求下列各式的值
3、求下列各式的x
下课
16.1.1 平方根(1) 授课教师: 梁文昌
第一周第一节八年级数学(下) 华师版教材南头初级中学初二级数学备课组一、教学目标1、掌握平方根及算术平方根的概念。
2、能够通过平方运算求一个非负数的平方根及算术平方根。
3、培养学生观察能力和概括问题的力。二、重点:平方根和算术平方根的 概念和性质。三、难点:平方根与算术平方根的
区别与联系。我们已学过了有理数的加法、减法、乘法、除法、乘方这五种运算。在这五种运算中那些是逆运算呢?★加法与减法互为逆运算;★乘法与除法互为逆运算;★那么乘方与谁互为逆运算呢?回忆与思考:我们先来复习乘方的有关内容:底数幂指数要剪出一张边长是5厘米的正方形纸片,它的面积是多少?这个问题实际上就是求:答:它的面积是25平方厘 米这是已知底数和指数,求幂的运算乘方运算我们把问题反过来,要做一张面积是25平方厘米的方桌面,它的边长是多少厘米? 实际上就是要求出一个数,使它的平方等于25,即:显然,括号里应是±5,但-5不符题意。∴方桌面的边长应是5厘米。25平方厘米认真观察下式可知:这是已知指数和幂求底数的运算,叫做开方运算。我们把括号里的±5叫做25的平方根(二次方根)。例如:∴3 和 -3 都是9的平方根。又例如:∴ 0.4 和 -0.4 都是0.16的平方根。 即0.16的平方根有两个,一个是+0.4;另一个是-0.4。 一个正数有两个平方根,这两个平方根互为相反数。∴ 零的平方根是零。这两个平方根互为相反数。∵任何数的平方都不可能是负数∴负数没有平方根通过上面的学习可以得到平方根的性质:★一个正数有两个平方根,它们互为相反数。★零的平方根是零。★负数没有平方根。 例1:判断下列各数有没有平方根,如果有平方根,试求出它的平方根;如果没有平方根,说明理由。我们来试一试,请看书中第2页试一试及课后练习1有,81的平方根是±9没有,因为负数没有平方根有,0的平方根是0有,49的平方根是±7没有,因为负数没有平方根想一想 “负数没有平方根”与“一个正数的平方根不能为负数”这两种说法正确吗? 求一个数的平方根(二次方根)的运算,叫做开平方,开平方运算的结果就是平方根。 根据乘方和开方的意义,我们已知道:乘方和开方运算互为逆运算。平方和开平方互为逆运算。求平方根的写法如下:
正数x的两个平方根可分别写作
(正号一般省略),我们可以合并成为
读作:正负根号x 例2:求下列各数的平方根。解: 我们可以这样考虑∴100的平方根是±10请你妨照上面的例子完成其余三个小题。我们定义正数a的正的平方根,叫做a的算术平方根.例如:100的算术平方根为10,记作 例3:求下列各数的算术平方根。
(1)144 (2)49 (3)2.25
0的算术平方根是多少呢?负数有算术平方根吗?算术平方根和平方根的关系是怎样的?问题:拓展思维:2、若一个正数的平方根为a+5和a+1,求a的值和这个正数。
1、求 和 的平方根和算术平方根。小结:这节课我们学到了哪些知识(1)如果一个数的平方等于a,这个数叫做a的平方根;
(2)正数a的平方根有两个,它们互为相反数,零的平方根是零,负数没有平方根;
(3)求一个数的平方根的运算叫做开平方,平方和开平方互为逆运算.作业 P7习题16.1 第1题课堂小测1、说出121、144、169、225、256、289、324、361的平方根。
2、求下列各式的值
3、求下列各式的x
下课
