《名师学典·数学》课件新人教19.1变量与函数第2课时
文档属性
| 名称 | 《名师学典·数学》课件新人教19.1变量与函数第2课时 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-23 12:32:37 | ||
图片预览






文档简介
(共16张PPT)
欢迎使用《名师学典·数学》学案配套课件
原创:xx22pp
1.如果水的流速量 3米/分(定量),那么每分钟的进水量
Q(立方米)与所选择的水管直径 D(米)之间的函数关系
是 .其中变量是 ,常量是 .
2.寄一封质量在20 g以内的市内平信,需邮资0.80元,则寄 x 封
这样的信所需邮资 y(元).试用含 x 的式子表示 y 是 ,
其中的常量是 ,变量是 .
3.如下表:
n 1 2 3 4 ······
y 2×1 4×3 6×5 8×7 ······
试研讨这里的 y 与 n 的关系式,并指出其中的变量.
答案:
1.
D,Q;
2.
y=0.8x;
0.8是常量,
x、y是变量
3.
y=2n(2n-1);
变量是y、n
19.1 变量与函数——函数
问题1~3中是否各有两个变量?同一个问题中的变量之间有
什么联系?
问题1 问题2 问题3
变量 D,Q x,y y,n
联系
y=0.8x
y=2n(2n-1)
归纳:
(1)上面几变化过程中,都有两个变量;
(2)当其中一个变量取定一个值时,另一个变量就有唯一确定的值与其对应
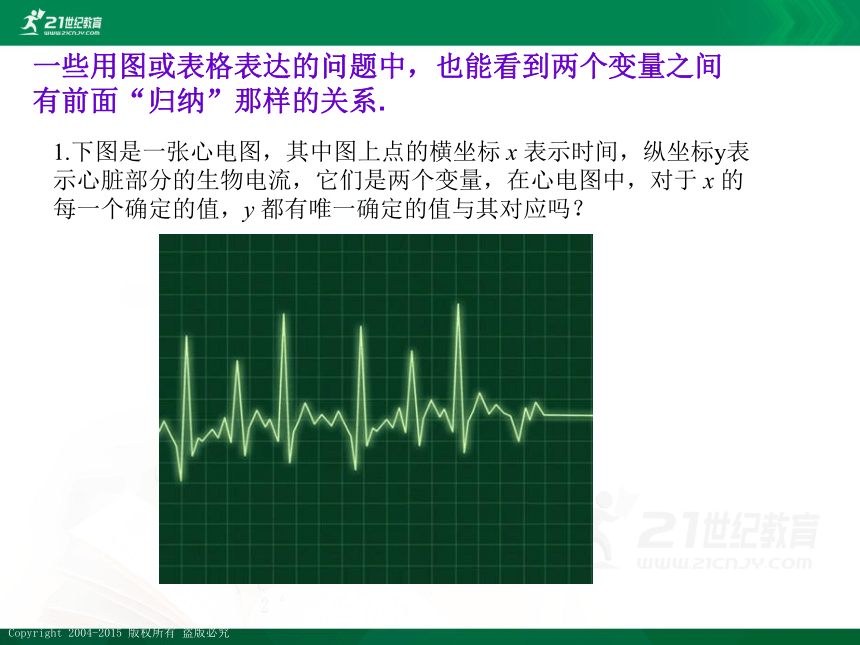
1.下图是一张心电图,其中图上点的横坐标 x 表示时间,纵坐标y表示心脏部分的生物电流,它们是两个变量,在心电图中,对于 x 的每一个确定的值,y 都有唯一确定的值与其对应吗?
一些用图或表格表达的问题中,也能看到两个变量之间有前面“归纳”那样的关系.
2.下面的我国人口数统计表中,年份与人口数可以分别记作两个变量x 与 y,对于表中每一个确定的年份 x,都对应着一个确定的人口数 y吗?
年份 人口数/亿
1984 10.34
1989 11.06
1994 11.76
1999 12.52
2010 13.71
总结:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y 都有唯一的值与其对应,那我们就说 x 是自变量,y 是 x的函数.如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
思考:如何判断一个函数呢?
前面的 , , ,也都是函数;心电图中的生物电流y是时间x的函数;从口数统计表中,人口数y是年份x的函数.
y=0.8x
y=2n(2n-1)
判定: 是否是函数,如果是请指出自变量.
请同学们判定以下哪些是函数,并指出自变量;
哪些不是函数?为什么?
自变量和函数
例1
在一个关系式 中,有两个变量为:Q、D,
∵当D=2时,函数值
∴当D为一个确定值时,Q有唯一的值与其对应,
所以x 是自变量,y 是 x的函数.
判断
(1)y=0.8x;(2)y=2n(2n-1);(3)y=±x;
(4)y=|x|;(5)x2+y2=1;(6)2x -3y=0;(7)y=x2
(1)(2)(4)(6)(7)是函数,(3)(5)不是函数
注意:(1)函数中的自变量的值确定时,函数值一定是唯一的.
(2)当函数值确定时,自变量的值可以有一个或有多个.
通过例题,进一步认识函数
例2
汽车油箱中有汽油50 L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程 x(单位:km)的增加而减少,
平均耗油量为0.1 L/km.
(1)写出表示 y 与 x 的函数关系的式子.
解:行驶路程 x 是自变量,油箱中的油量y是x的函数,
根据:油箱中的油量=原有汽油量-行驶消耗的油量
得到它们的关系为:y=50-0.1x
用x的代数式表示y
(2)指出自变量 x 的取值范围.
解:仅从式子根据题意,可得x≥0,y≥0,
仅从式子y=20-0.1x看,x可以取任何实数.
但x代表的实际意义为行驶路程,因此x不能取负数.
行驶中的耗油量为0.1x,它不能超过油箱中现有汽油量50,即0.1x≤50,
因此,自变量x的取值范围是0≤x≤500.
自变量x能取任何实数吗?
(3)当汽车行驶200km时,油箱中还有多少汽油?
当汽车行驶200km时,油箱中的汽油量是函数y=50-0.1x在x=200时的函数值.
解:将x=200代入y=20-0.1x,得
y=50-0.1×200=30.
当汽车行驶200km时,油箱中还有30L汽油.
概念
像y=50-0.1x这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述常用方法.这种式子叫做函数的解析式.
练一练
1.下列关系中,y不是x函数的是( )
A. B. C. D.
2.火车以40千米/时的速度行驶,它走过的路程s(千米)与时间
t(小时)的函数解析式是 ,其中自变量是 .
3.学校举行校园歌手大奖赛,参加决赛的6名选手最后取得的成绩如
下表所示:
选手序号 1 2 3 4 5 6
成绩 97.7 98.4 96.5 97.3 96.5 98.1
下列的两个说法:
(1)成绩是序号的函数. (2)序号是成绩的函数.
说法正确的是(填序号即可) .
4.一石激起千层浪,一枚石头投入水中,会在水面上激起一圈圈圆形涟漪,
如图所示(这些圆的圆心相同).
(1)在这个变化过程中,自变量是 .
(2)如果圆的半径为r,面积为S,则S与r的函数解析式是 .
(3)当圆的半径由1cm增加到5cm时,面积增加了 cm2.
5.写出下列函数中自变量x的取值范围:
(1)y=2x-3;(2) ;(3) ; (4)
答案:1.D 2.s=40t ,t 3.(2) 4.(1)r (2) (3)
5.(1)x取任何实数;(2)x≠1;(3)x≤4; (4)x≥1且x≠2.
方法总结
1
写函数解析式时,就是用自变量的代数示来表示函数.
2
求自变量的范围时,首先从函数解析式看,再从自变量所代表的意义看,再从函数值看.
3
当已知自变量的值或函数值时,将其代入函数解析式,化成一个一元一次方程,求出即可.
课内练习
1.下面每个选项中给出了某个变化过程中的两个变量x和y,其中
y不是x的函数的选项是( )
A.y:正方形的面积,x:这个正方形的周长
B.y:某班学生的身高,x:这个班学生的学号
C.y:圆的面积,x:这个圆的直径
D.y:一个正数的平方根,x:这个正数
2.下列函数中,自变量x的取值范围是x≥3的是( )
A. B. C. D.
3.下列函数中,与y=|x|表示同一个函数的是( )
A. B. C. D.
4.当x=0时,函数y=2x2+1的值是( )
A.1 B.0 C.3 D.-1
5.已知方程x-3y=12,用含x的代数式表示y是 .
6.邓教师设计一个计算程序,输入和输出的数据如下表所示:
那么当输入数据是正整数n时,输出的数据是 .
输入数据 1 2 3 4 5 6 ······
输出数据 ······
7.按图示的运算程序,输入一个实数x,便可输出一个相应的实
数y,写出y与x之间的函数关系式:y= .
输入x
输入y
-4
×5
+2
9.我们把y(x)和y(-x)相等的函数称为奇函数.看下面一道例题求证:
例题:已知y=3x+3,求证y=3x+3的奇偶性.
解:y(x)=3x+3,y(-x)=-3x+3,∵y(x)≠y(-x),∴y=3x+3为奇函数.
已知y=3x2+2x-1,判断y=3x2+2x-1的奇偶性,并说明理由.
8.如图,长方形ABCD中,AB=4,BC=8.点P在AB上运动,设
PB=x,图中阴影部分的面积为y.
(1)写出阴影部分的面积y与x之间的函数解析式和自变量x的取值范围;
(2)点P在什么位置时,阴影部分的面积等于20?
课时总结
1.理解自变量、函数、函数值和解析式的概念;
2.会求自变量的取值范围;
3.会求函数角析式;
4.会求函数值 或自变量.
谢谢观赏
《名师学典·数学》 课件
让数学更有趣!——xx22pp
欢迎使用《名师学典·数学》学案配套课件
原创:xx22pp
1.如果水的流速量 3米/分(定量),那么每分钟的进水量
Q(立方米)与所选择的水管直径 D(米)之间的函数关系
是 .其中变量是 ,常量是 .
2.寄一封质量在20 g以内的市内平信,需邮资0.80元,则寄 x 封
这样的信所需邮资 y(元).试用含 x 的式子表示 y 是 ,
其中的常量是 ,变量是 .
3.如下表:
n 1 2 3 4 ······
y 2×1 4×3 6×5 8×7 ······
试研讨这里的 y 与 n 的关系式,并指出其中的变量.
答案:
1.
D,Q;
2.
y=0.8x;
0.8是常量,
x、y是变量
3.
y=2n(2n-1);
变量是y、n
19.1 变量与函数——函数
问题1~3中是否各有两个变量?同一个问题中的变量之间有
什么联系?
问题1 问题2 问题3
变量 D,Q x,y y,n
联系
y=0.8x
y=2n(2n-1)
归纳:
(1)上面几变化过程中,都有两个变量;
(2)当其中一个变量取定一个值时,另一个变量就有唯一确定的值与其对应
1.下图是一张心电图,其中图上点的横坐标 x 表示时间,纵坐标y表示心脏部分的生物电流,它们是两个变量,在心电图中,对于 x 的每一个确定的值,y 都有唯一确定的值与其对应吗?
一些用图或表格表达的问题中,也能看到两个变量之间有前面“归纳”那样的关系.
2.下面的我国人口数统计表中,年份与人口数可以分别记作两个变量x 与 y,对于表中每一个确定的年份 x,都对应着一个确定的人口数 y吗?
年份 人口数/亿
1984 10.34
1989 11.06
1994 11.76
1999 12.52
2010 13.71
总结:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y 都有唯一的值与其对应,那我们就说 x 是自变量,y 是 x的函数.如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
思考:如何判断一个函数呢?
前面的 , , ,也都是函数;心电图中的生物电流y是时间x的函数;从口数统计表中,人口数y是年份x的函数.
y=0.8x
y=2n(2n-1)
判定: 是否是函数,如果是请指出自变量.
请同学们判定以下哪些是函数,并指出自变量;
哪些不是函数?为什么?
自变量和函数
例1
在一个关系式 中,有两个变量为:Q、D,
∵当D=2时,函数值
∴当D为一个确定值时,Q有唯一的值与其对应,
所以x 是自变量,y 是 x的函数.
判断
(1)y=0.8x;(2)y=2n(2n-1);(3)y=±x;
(4)y=|x|;(5)x2+y2=1;(6)2x -3y=0;(7)y=x2
(1)(2)(4)(6)(7)是函数,(3)(5)不是函数
注意:(1)函数中的自变量的值确定时,函数值一定是唯一的.
(2)当函数值确定时,自变量的值可以有一个或有多个.
通过例题,进一步认识函数
例2
汽车油箱中有汽油50 L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程 x(单位:km)的增加而减少,
平均耗油量为0.1 L/km.
(1)写出表示 y 与 x 的函数关系的式子.
解:行驶路程 x 是自变量,油箱中的油量y是x的函数,
根据:油箱中的油量=原有汽油量-行驶消耗的油量
得到它们的关系为:y=50-0.1x
用x的代数式表示y
(2)指出自变量 x 的取值范围.
解:仅从式子根据题意,可得x≥0,y≥0,
仅从式子y=20-0.1x看,x可以取任何实数.
但x代表的实际意义为行驶路程,因此x不能取负数.
行驶中的耗油量为0.1x,它不能超过油箱中现有汽油量50,即0.1x≤50,
因此,自变量x的取值范围是0≤x≤500.
自变量x能取任何实数吗?
(3)当汽车行驶200km时,油箱中还有多少汽油?
当汽车行驶200km时,油箱中的汽油量是函数y=50-0.1x在x=200时的函数值.
解:将x=200代入y=20-0.1x,得
y=50-0.1×200=30.
当汽车行驶200km时,油箱中还有30L汽油.
概念
像y=50-0.1x这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述常用方法.这种式子叫做函数的解析式.
练一练
1.下列关系中,y不是x函数的是( )
A. B. C. D.
2.火车以40千米/时的速度行驶,它走过的路程s(千米)与时间
t(小时)的函数解析式是 ,其中自变量是 .
3.学校举行校园歌手大奖赛,参加决赛的6名选手最后取得的成绩如
下表所示:
选手序号 1 2 3 4 5 6
成绩 97.7 98.4 96.5 97.3 96.5 98.1
下列的两个说法:
(1)成绩是序号的函数. (2)序号是成绩的函数.
说法正确的是(填序号即可) .
4.一石激起千层浪,一枚石头投入水中,会在水面上激起一圈圈圆形涟漪,
如图所示(这些圆的圆心相同).
(1)在这个变化过程中,自变量是 .
(2)如果圆的半径为r,面积为S,则S与r的函数解析式是 .
(3)当圆的半径由1cm增加到5cm时,面积增加了 cm2.
5.写出下列函数中自变量x的取值范围:
(1)y=2x-3;(2) ;(3) ; (4)
答案:1.D 2.s=40t ,t 3.(2) 4.(1)r (2) (3)
5.(1)x取任何实数;(2)x≠1;(3)x≤4; (4)x≥1且x≠2.
方法总结
1
写函数解析式时,就是用自变量的代数示来表示函数.
2
求自变量的范围时,首先从函数解析式看,再从自变量所代表的意义看,再从函数值看.
3
当已知自变量的值或函数值时,将其代入函数解析式,化成一个一元一次方程,求出即可.
课内练习
1.下面每个选项中给出了某个变化过程中的两个变量x和y,其中
y不是x的函数的选项是( )
A.y:正方形的面积,x:这个正方形的周长
B.y:某班学生的身高,x:这个班学生的学号
C.y:圆的面积,x:这个圆的直径
D.y:一个正数的平方根,x:这个正数
2.下列函数中,自变量x的取值范围是x≥3的是( )
A. B. C. D.
3.下列函数中,与y=|x|表示同一个函数的是( )
A. B. C. D.
4.当x=0时,函数y=2x2+1的值是( )
A.1 B.0 C.3 D.-1
5.已知方程x-3y=12,用含x的代数式表示y是 .
6.邓教师设计一个计算程序,输入和输出的数据如下表所示:
那么当输入数据是正整数n时,输出的数据是 .
输入数据 1 2 3 4 5 6 ······
输出数据 ······
7.按图示的运算程序,输入一个实数x,便可输出一个相应的实
数y,写出y与x之间的函数关系式:y= .
输入x
输入y
-4
×5
+2
9.我们把y(x)和y(-x)相等的函数称为奇函数.看下面一道例题求证:
例题:已知y=3x+3,求证y=3x+3的奇偶性.
解:y(x)=3x+3,y(-x)=-3x+3,∵y(x)≠y(-x),∴y=3x+3为奇函数.
已知y=3x2+2x-1,判断y=3x2+2x-1的奇偶性,并说明理由.
8.如图,长方形ABCD中,AB=4,BC=8.点P在AB上运动,设
PB=x,图中阴影部分的面积为y.
(1)写出阴影部分的面积y与x之间的函数解析式和自变量x的取值范围;
(2)点P在什么位置时,阴影部分的面积等于20?
课时总结
1.理解自变量、函数、函数值和解析式的概念;
2.会求自变量的取值范围;
3.会求函数角析式;
4.会求函数值 或自变量.
谢谢观赏
《名师学典·数学》 课件
让数学更有趣!——xx22pp
