12.1 平方根[上学期]

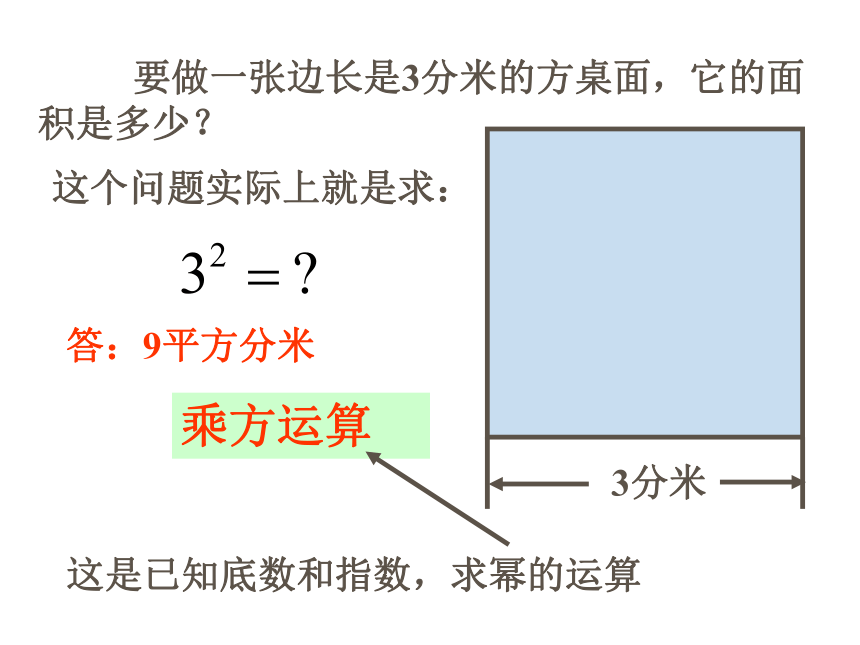
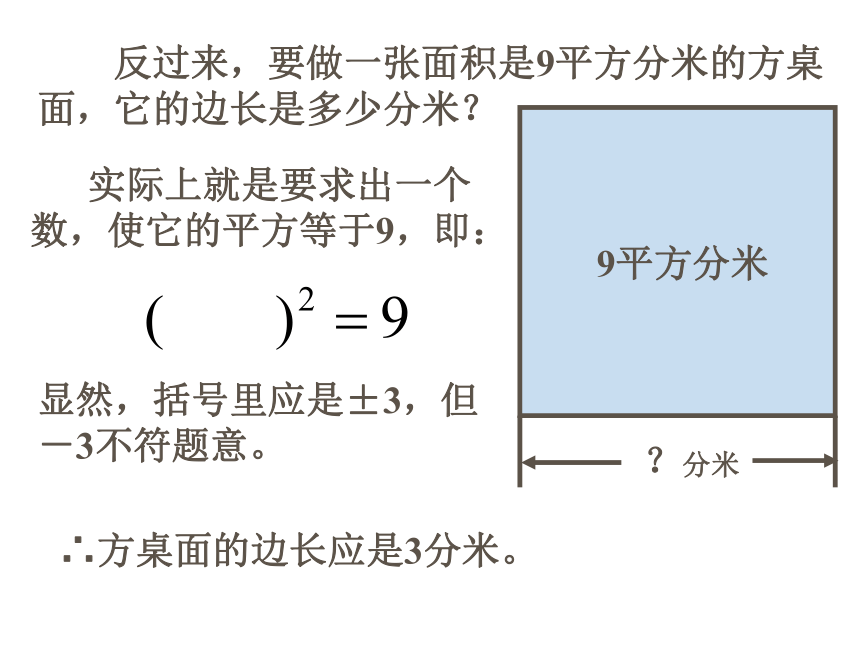
课件17张PPT。平方根的意义 我们已学过了有理数的加法、减法、乘法、除法、乘方这五种运算。在这五种运算中：★加法与减法互为逆运算；★乘法与除法互为逆运算；★那么乘方与谁互为逆运算呢？回忆与思考：本节课我们就来学习研究这个问题。先复习有关内容：底数幂指数 要做一张边长是3分米的方桌面，它的面积是多少？这个问题实际上就是求：答：9平方分米这是已知底数和指数，求幂的运算乘方运算 反过来，要做一张面积是9平方分米的方桌面，它的边长是多少分米？ 实际上就是要求出一个数，使它的平方等于9，即：显然，括号里应是±3，但－3不符题意。∴方桌面的边长应是3分米。9平方分米认真观察下式可知：这是已知指数和幂求底数的运算，叫做开方运算。我们把括号里的±3叫做9的平方根（二次方根）。例如：∴5 和 －5 都是25的平方根。又例如：∴ 0.4 和 －0.4 都是0.16的平方根。 即0.16的平方根有两个，一个是＋0.4；另一个是－0.4，这两个平方根互为相反数。 注意：一个正数有两个平方根，这两个平方根互为相反数。∴ 零的平方根是零。∵任何数的平方都不可能是负数∴负数没有平方根通过上面的学习可以得到平方根的性质：★一个正数有两个平方根，它们互为相反数。★零的平方根是零。★负数没有平方根。想一想 “负数没有平方根”与“一个数的平方根不能为负数”意义是否一样？现在我们更加明确开方运算的意义了 求一个数的平方根（二次方根）的运算，叫做开平方，开平方运算的结果就是平方根。 根据乘方和开方的意义，我们已知道：乘方和开方运算互为逆运算。当然，平方和开平方互为逆运算。平方根的表示法：被开方数平方根根指数注意：根指数是2 时，通常省略不写。举一个实际例子吧！ 例1：判断下列各数有没有平方根，如果有平方根，试求出它的平方根；如果没有平方根，说明理由。 例2：求下列各数的平方根。解： （1）∴100的平方根是±10请你妨照上面的例子完成其余三个小题。作业习题16.1 1题 、4题 ；
同步训练与测评 第一页 1—8小题。再见！