平方根(一)[上学期]
图片预览










文档简介
课件31张PPT。心有多大,
舞台就有多大!!!
放飞你的思想,
好好学习吧!!!第12章 数的开方§1.平方根与立方根
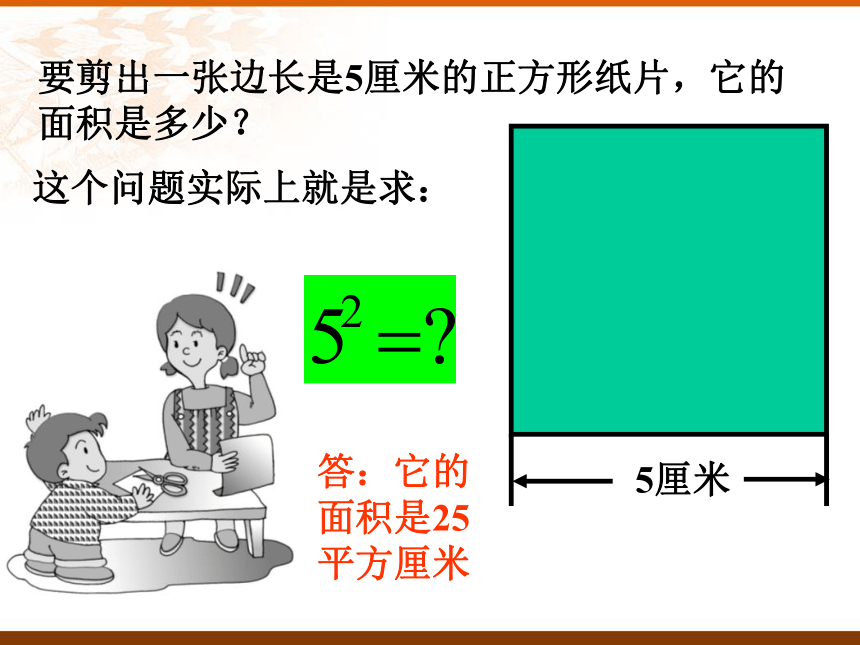
——平方根我们已学过了有理数的加法、减法、乘法、除法、乘方这五种运算。在这五种运算中那些是逆运算呢?★加法与减法互为逆运算;★乘法与除法互为逆运算;★那么乘方与谁互为逆运算呢?回忆与思考:我们先来复习乘方的有关内容:底数幂指数要剪出一张边长是5厘米的正方形纸片,它的面积是多少?这个问题实际上就是求:答:它的面积是25平方厘米情景问题: 邻居张大爷家新买了25只羊,要用栅栏围成一个正方形羊圈,如果每只羊占用1平方米,那么这个羊圈的边长需要多长? 本章将学习有关数的
一种新的运算——开方; 观察与概括上面的问题实质上就是找一个数,这个数的平方等于25。平方根:如果一个数的平方等于a,那么这个数
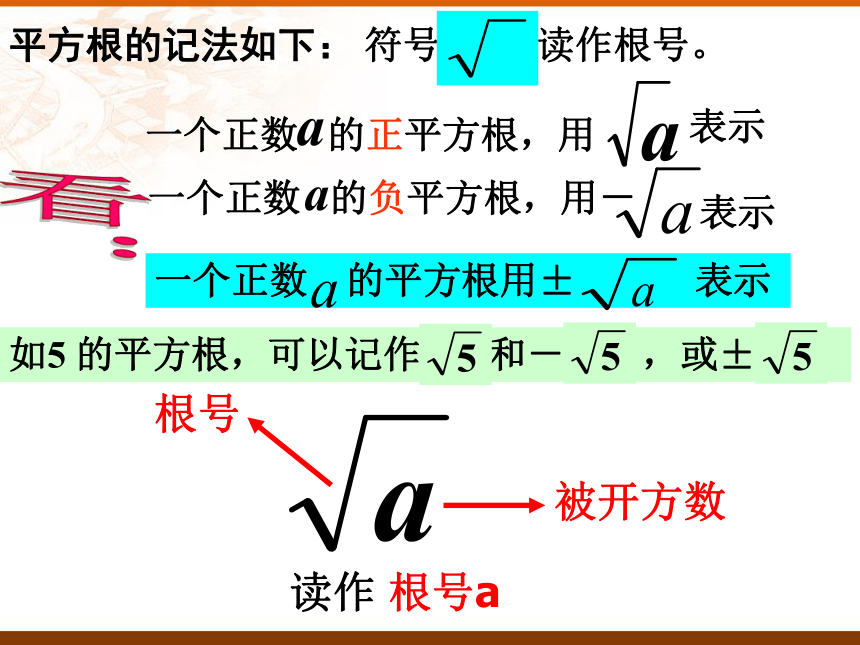
叫做a的平方根 。思考: (1)25的平方根只有一个5吗?表示看:平方根的记法如下:读作 根号a例如:∴3 和 -3 都是9的平方根。又例如:∴ 0.4 和 -0.4 都是0.16的平方根。∴ 零的平方根是零。∵任何数的平方都不可能是负数∴负数没有平方根思考:负数有平方根吗?试一试
(1) 144的平方根是什么?(4) -4有没有平方根?(2) 0的平方根是什么?为什么?∵122=144, (-12)2=144 ∴144的平方根是±12.∵02=0, ∴0的平方根是0.思考:解决以上问题后,你能说说一个数的平方根有什么特征吗?通过上面的学习可以得到:★一个正数有正、负两个平方根,它们互为相反数。★零的平方根是零。★负数没有平方根。平方根的性质 例1:判断下列各数有没有平方根,如果有平方根,试求出它的平方根;如果没有平方根,说明理由。有,81的平方根是±9没有,因为负数没有平方根有,0的平方根是0有,49的平方根是±7没有,因为负数没有平方根 例2:求下列各数的平方根。解:∴100的平方根是±10请你妨照上面的例子完成其余三个小题。★ 一个正数有两个平方根,它们互为相反数。★ 零的平方根是零。★ 负数没有平方根。小结:一个正数有两个平方根,它们互为相反数。如: +3 和-3都是9的平方根+3是9正的平方根,我们把它叫做9的算术平方根 正数a的正的平方根,叫做a的算术平方根 正数a的正的平方根,叫做a的算术平方根 a称为被开方数. 0的平方根只有一个,就是0.我们规定:7的算术平方根记作 ,平方根记作 , 例3:求下列各数的算术平方根。
(1)144 (2)49 (3)2.25
0的算术平方根是多少呢?负数有算术平方根吗?算术平方根和平方根的关系是怎样的?想一想求一个数a的平方根的运算,叫做开平方。149+1-1+2-2+3-3149+1-1+2-2+3-3开平方平方将一个正数开平方,关键是找出它的一个算术平方根.巩固练习:例1、将下列各数开平方:(1)49 (2)1.69 (×)(×)(×)(×)(√)(√)判断下列说法是否正确.1. 的平方根是±16. ( ) 2. 一定是正数. ( ) 3.a2的算术平方根是a. ( )4.若 , 则a=-5. ( )5. ( )6.-6是(-6)2的平方根. ( ) 7.若x2=36,则x= ( ) ×××××√√练习:求下列各数有没有平方根?如果有的话,求出它的平方根;如果没有平方根,请说明理由。25,0.09,-0.36,49,0.01,0练 习
说出下列各数的平方根;
(1)64;(2)0.25;(3) ; (4)61、写出下列各数的平方根:
(1)49; (2)1600;
(3)169; (4)0.81;
(5)0.0036; (6)1.44;
练一练*2、写出下列各数的平方根:
(1)50; (2)1000.如果一个数X的平方等于a,即 X2 = a,
那么这个数X叫做a的平方根(二次方根)a的平方根表示为x2 = a求数a的平方根的运算叫做开平方? 今天你学到了什么 ? ★ 一个正数有两个平方根,它们互为相反数。★ 零的平方根是零。★ 负数没有平方根。如果一个数的平方等于a,那么这个数叫做a的平方根。正数a的正的平方根,叫做a的算术平方根 求一个数的平方根的运算叫做开平方.非负数的非负平方根叫做算术平方根.你记住平方根与算术平方根的区别和联系了吗? 算术平方根的双非负性课堂小测1、说出121、144、169、225、256、289、324、361的平方根。
2、求下列各式的值
比一比——看谁最聪明? 如图,求左圈和右圈中的“?”表示的数: 作业习题12.1 1题 ;再见祝学习快乐
舞台就有多大!!!
放飞你的思想,
好好学习吧!!!第12章 数的开方§1.平方根与立方根
——平方根我们已学过了有理数的加法、减法、乘法、除法、乘方这五种运算。在这五种运算中那些是逆运算呢?★加法与减法互为逆运算;★乘法与除法互为逆运算;★那么乘方与谁互为逆运算呢?回忆与思考:我们先来复习乘方的有关内容:底数幂指数要剪出一张边长是5厘米的正方形纸片,它的面积是多少?这个问题实际上就是求:答:它的面积是25平方厘米情景问题: 邻居张大爷家新买了25只羊,要用栅栏围成一个正方形羊圈,如果每只羊占用1平方米,那么这个羊圈的边长需要多长? 本章将学习有关数的
一种新的运算——开方; 观察与概括上面的问题实质上就是找一个数,这个数的平方等于25。平方根:如果一个数的平方等于a,那么这个数
叫做a的平方根 。思考: (1)25的平方根只有一个5吗?表示看:平方根的记法如下:读作 根号a例如:∴3 和 -3 都是9的平方根。又例如:∴ 0.4 和 -0.4 都是0.16的平方根。∴ 零的平方根是零。∵任何数的平方都不可能是负数∴负数没有平方根思考:负数有平方根吗?试一试
(1) 144的平方根是什么?(4) -4有没有平方根?(2) 0的平方根是什么?为什么?∵122=144, (-12)2=144 ∴144的平方根是±12.∵02=0, ∴0的平方根是0.思考:解决以上问题后,你能说说一个数的平方根有什么特征吗?通过上面的学习可以得到:★一个正数有正、负两个平方根,它们互为相反数。★零的平方根是零。★负数没有平方根。平方根的性质 例1:判断下列各数有没有平方根,如果有平方根,试求出它的平方根;如果没有平方根,说明理由。有,81的平方根是±9没有,因为负数没有平方根有,0的平方根是0有,49的平方根是±7没有,因为负数没有平方根 例2:求下列各数的平方根。解:∴100的平方根是±10请你妨照上面的例子完成其余三个小题。★ 一个正数有两个平方根,它们互为相反数。★ 零的平方根是零。★ 负数没有平方根。小结:一个正数有两个平方根,它们互为相反数。如: +3 和-3都是9的平方根+3是9正的平方根,我们把它叫做9的算术平方根 正数a的正的平方根,叫做a的算术平方根 正数a的正的平方根,叫做a的算术平方根 a称为被开方数. 0的平方根只有一个,就是0.我们规定:7的算术平方根记作 ,平方根记作 , 例3:求下列各数的算术平方根。
(1)144 (2)49 (3)2.25
0的算术平方根是多少呢?负数有算术平方根吗?算术平方根和平方根的关系是怎样的?想一想求一个数a的平方根的运算,叫做开平方。149+1-1+2-2+3-3149+1-1+2-2+3-3开平方平方将一个正数开平方,关键是找出它的一个算术平方根.巩固练习:例1、将下列各数开平方:(1)49 (2)1.69 (×)(×)(×)(×)(√)(√)判断下列说法是否正确.1. 的平方根是±16. ( ) 2. 一定是正数. ( ) 3.a2的算术平方根是a. ( )4.若 , 则a=-5. ( )5. ( )6.-6是(-6)2的平方根. ( ) 7.若x2=36,则x= ( ) ×××××√√练习:求下列各数有没有平方根?如果有的话,求出它的平方根;如果没有平方根,请说明理由。25,0.09,-0.36,49,0.01,0练 习
说出下列各数的平方根;
(1)64;(2)0.25;(3) ; (4)61、写出下列各数的平方根:
(1)49; (2)1600;
(3)169; (4)0.81;
(5)0.0036; (6)1.44;
练一练*2、写出下列各数的平方根:
(1)50; (2)1000.如果一个数X的平方等于a,即 X2 = a,
那么这个数X叫做a的平方根(二次方根)a的平方根表示为x2 = a求数a的平方根的运算叫做开平方? 今天你学到了什么 ? ★ 一个正数有两个平方根,它们互为相反数。★ 零的平方根是零。★ 负数没有平方根。如果一个数的平方等于a,那么这个数叫做a的平方根。正数a的正的平方根,叫做a的算术平方根 求一个数的平方根的运算叫做开平方.非负数的非负平方根叫做算术平方根.你记住平方根与算术平方根的区别和联系了吗? 算术平方根的双非负性课堂小测1、说出121、144、169、225、256、289、324、361的平方根。
2、求下列各式的值
比一比——看谁最聪明? 如图,求左圈和右圈中的“?”表示的数: 作业习题12.1 1题 ;再见祝学习快乐
