第2课时 反比例-人教版数学六年级下册第四单元课件(共21张PPT)
文档属性
| 名称 | 第2课时 反比例-人教版数学六年级下册第四单元课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-16 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
第 2 课时
反比例
2.正比例和反比例
第4单元 比 例
复习导入
1.说一说什么是成正比例的量。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量。
2.判断下面各题中的两种量是否成正比例关系。
(1)长方形的长一定,它的宽和面积。
(2)圆的周长和半径。
(3)一个人的年龄和他的身高。
成正比例关系
成正比例关系
不成比例
探究新知
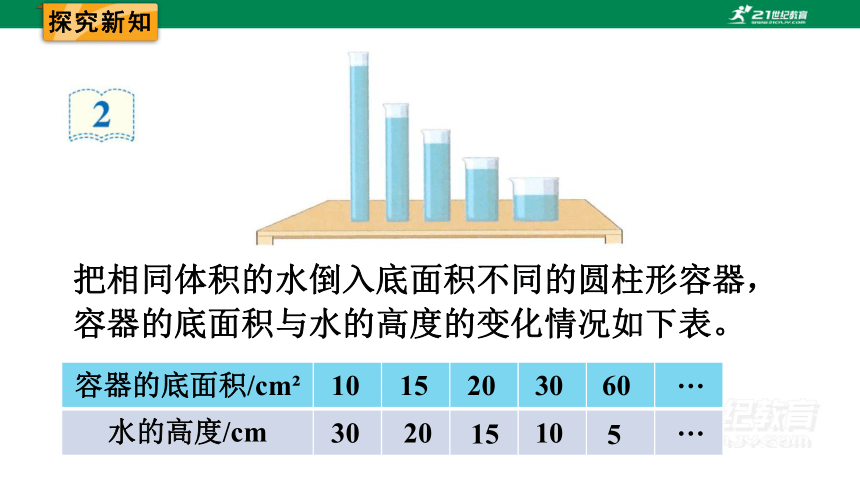
把相同体积的水倒入底面积不同的圆柱形容器,
容器的底面积与水的高度的变化情况如下表。
容器的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
容器的底面积/cm 10 15 20 30 60 ...
水的高度/cm 30 20 15 10 5 ...
根据上表,回答下面的问题。
(1)表中有哪两种量?
容器的底面积和水的高度。
(2)水的高度是怎样随着容器底面积的大小变化而变化的?
水的高度随着容器底面积的增大而减小。
容器的底面积/cm 10 15 20 30 60 ...
水的高度/cm 30 20 15 10 5 ...
容器的底面积/cm 10 15 20 30 60 ...
水的高度/cm 30 20 15 10 5 ...
(3)相对应的容器的底面积与水的高度的乘积分别是多少?
300
300
300
300
300
300
体积/cm3
水的高度和底面积的变化有什么规律?
底面积×高度=体积
(一定)
归纳总结
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系。
如果用字母 x 和 y 表示两种相关联的量,用 k 表示它们的积(一定),反比例关系可以用下面的式子表示:
x y=k
(一定)
如果长方形的面积一定,长与宽成反比例关系。
你能举出生活中反比例关系的例子吗?
如果总价一定,单价与数量成反比例关系。
填一填。
名称 共同点 不同点
特征 关系式
正比例 关系 两种( )的量,一种量( ),另一种量也随着( )。 两种量中相对应的两个数的( )一定。
反比例 关系 两种量中相对应的两个数的( )一定。
一定
( )×( )
=
( )
一定
相关联
变化
变化
比值
乘积
y
x
k
x
y
k
巩固运用
每天运的质量/t
运货的天数/天
(1)表中有哪两种量?它们是不是相关联的量?
这两种量是相关联的量。
1.运输队要运一批货物,每天运的质量和运货的天数之间的关系如下。
50
6
300
1
150
2
100
3
75
4
60
5
(教材P46 做一做)
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说一说这个积表示什么。
300×1=300 150×2=300 100×3=300 75×4=300 60×5=300 50×6=300
每天运的质量/吨
运货的天数/天
300
1
150
2
100
3
75
4
60
5
50
6
乘积都相等(一定),这个积表示这批货的总量。
(3)运货的天数与每天运的吨数成反比例关系吗?为什么?
x
运货的天数
每天运的吨数
y
x×y=300
(一定)
成反比例关系
每天运的质量/吨
运货的天数/天
300
1
150
2
100
3
75
4
60
5
50
6
2.给一间长9m、宽6m的教室铺地砖,每块地砖的面积与所需地砖数量如下表。
所需地砖数量与每块地砖的面积是否成反比例关系?为什么?
成反比例关系,因为教室的面积一定,而每块地砖的面积与所需地砖数量的乘积都等于教室的面积。
(教材P49 练习九T8)
3.判断下面各题中的两种量是否成反比例关系,并说明理由。
(1)煤的数量一定,使用天数与平均每天的用煤量。
成反比例关系。因为平均每天的用煤量×使用天数=煤的数量(一定),所以使用天数与平均每天的用煤量成反比例关系。
(教材P49 练习九T11)
(2)全班的人数一定,按各组人数相等的要求分组,组数与每组的人数。
成反比例关系。因为每组的人数×组数=全班的人数(一定),所以组数与每组的人数成反比例关系。
(3)圆柱的体积一定,圆柱的底面积与高。
成反比例关系。因为圆柱的底面积×高=圆柱体积(一定),所以圆柱的底面积与高成反比例关系。
(4)在一块菜地上只种黄瓜与西红柿两种作物,
这两种作物的种植面积。
不成反比例关系。因为种黄瓜的面积与种西红柿的面积的和一定,而它们的乘积不一定,所以种黄瓜的面积与种西红柿的面积不成反比例关系。
(5)书的总册数一定,按每包册数相等的规定包装书,包数与每包的册数。
成反比例关系。因为每包的册数×包数=书的总册数(一定),所以包数与每包的册数成反比例关系。
课堂总结
通过这节课的学习,
你有什么收获
第 2 课时
反比例
2.正比例和反比例
第4单元 比 例
复习导入
1.说一说什么是成正比例的量。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量。
2.判断下面各题中的两种量是否成正比例关系。
(1)长方形的长一定,它的宽和面积。
(2)圆的周长和半径。
(3)一个人的年龄和他的身高。
成正比例关系
成正比例关系
不成比例
探究新知
把相同体积的水倒入底面积不同的圆柱形容器,
容器的底面积与水的高度的变化情况如下表。
容器的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
容器的底面积/cm 10 15 20 30 60 ...
水的高度/cm 30 20 15 10 5 ...
根据上表,回答下面的问题。
(1)表中有哪两种量?
容器的底面积和水的高度。
(2)水的高度是怎样随着容器底面积的大小变化而变化的?
水的高度随着容器底面积的增大而减小。
容器的底面积/cm 10 15 20 30 60 ...
水的高度/cm 30 20 15 10 5 ...
容器的底面积/cm 10 15 20 30 60 ...
水的高度/cm 30 20 15 10 5 ...
(3)相对应的容器的底面积与水的高度的乘积分别是多少?
300
300
300
300
300
300
体积/cm3
水的高度和底面积的变化有什么规律?
底面积×高度=体积
(一定)
归纳总结
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系。
如果用字母 x 和 y 表示两种相关联的量,用 k 表示它们的积(一定),反比例关系可以用下面的式子表示:
x y=k
(一定)
如果长方形的面积一定,长与宽成反比例关系。
你能举出生活中反比例关系的例子吗?
如果总价一定,单价与数量成反比例关系。
填一填。
名称 共同点 不同点
特征 关系式
正比例 关系 两种( )的量,一种量( ),另一种量也随着( )。 两种量中相对应的两个数的( )一定。
反比例 关系 两种量中相对应的两个数的( )一定。
一定
( )×( )
=
( )
一定
相关联
变化
变化
比值
乘积
y
x
k
x
y
k
巩固运用
每天运的质量/t
运货的天数/天
(1)表中有哪两种量?它们是不是相关联的量?
这两种量是相关联的量。
1.运输队要运一批货物,每天运的质量和运货的天数之间的关系如下。
50
6
300
1
150
2
100
3
75
4
60
5
(教材P46 做一做)
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说一说这个积表示什么。
300×1=300 150×2=300 100×3=300 75×4=300 60×5=300 50×6=300
每天运的质量/吨
运货的天数/天
300
1
150
2
100
3
75
4
60
5
50
6
乘积都相等(一定),这个积表示这批货的总量。
(3)运货的天数与每天运的吨数成反比例关系吗?为什么?
x
运货的天数
每天运的吨数
y
x×y=300
(一定)
成反比例关系
每天运的质量/吨
运货的天数/天
300
1
150
2
100
3
75
4
60
5
50
6
2.给一间长9m、宽6m的教室铺地砖,每块地砖的面积与所需地砖数量如下表。
所需地砖数量与每块地砖的面积是否成反比例关系?为什么?
成反比例关系,因为教室的面积一定,而每块地砖的面积与所需地砖数量的乘积都等于教室的面积。
(教材P49 练习九T8)
3.判断下面各题中的两种量是否成反比例关系,并说明理由。
(1)煤的数量一定,使用天数与平均每天的用煤量。
成反比例关系。因为平均每天的用煤量×使用天数=煤的数量(一定),所以使用天数与平均每天的用煤量成反比例关系。
(教材P49 练习九T11)
(2)全班的人数一定,按各组人数相等的要求分组,组数与每组的人数。
成反比例关系。因为每组的人数×组数=全班的人数(一定),所以组数与每组的人数成反比例关系。
(3)圆柱的体积一定,圆柱的底面积与高。
成反比例关系。因为圆柱的底面积×高=圆柱体积(一定),所以圆柱的底面积与高成反比例关系。
(4)在一块菜地上只种黄瓜与西红柿两种作物,
这两种作物的种植面积。
不成反比例关系。因为种黄瓜的面积与种西红柿的面积的和一定,而它们的乘积不一定,所以种黄瓜的面积与种西红柿的面积不成反比例关系。
(5)书的总册数一定,按每包册数相等的规定包装书,包数与每包的册数。
成反比例关系。因为每包的册数×包数=书的总册数(一定),所以包数与每包的册数成反比例关系。
课堂总结
通过这节课的学习,
你有什么收获
