平方根[上学期]
图片预览


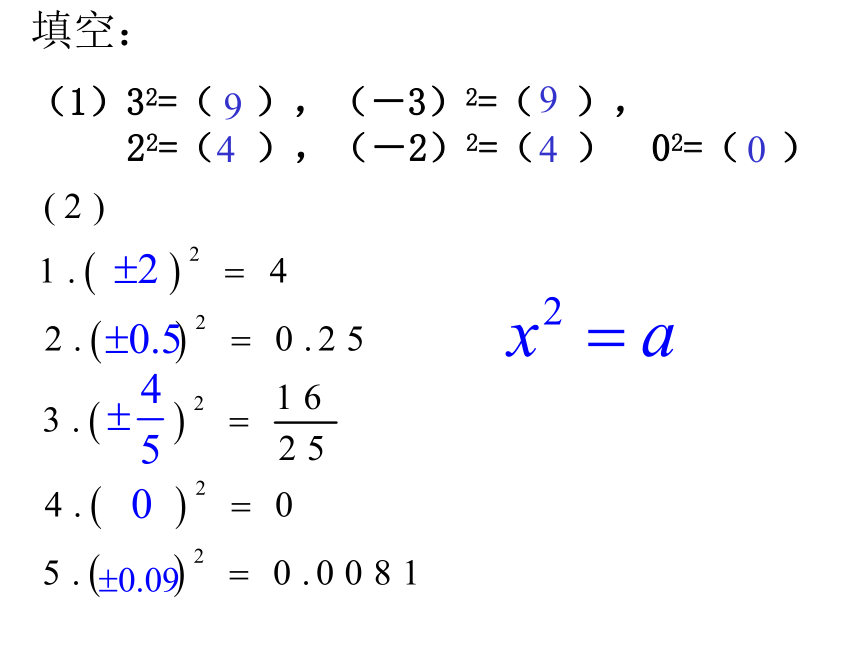


文档简介
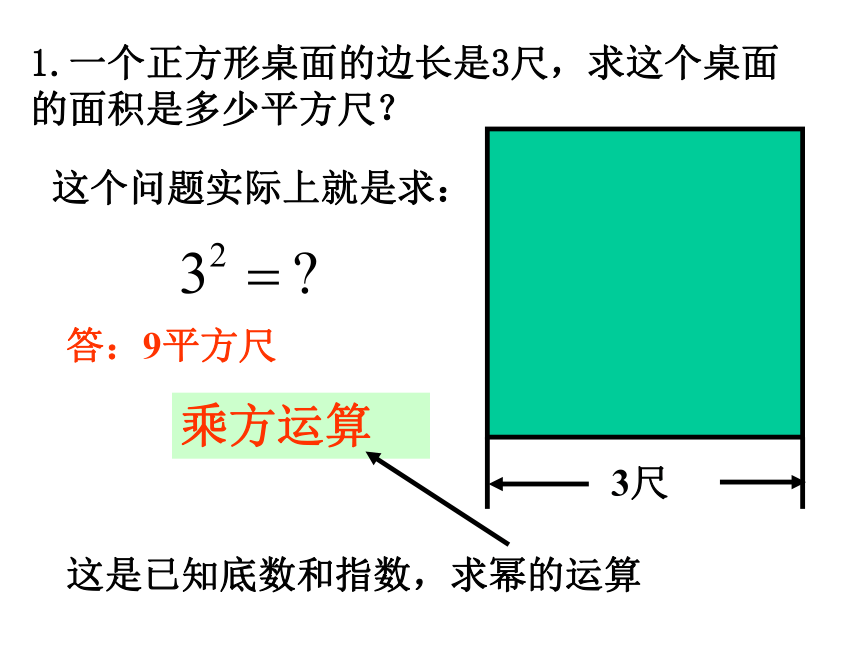
课件15张PPT。10.1平方根1.一个正方形桌面的边长是3尺,求这个桌面的面积是多少平方尺?
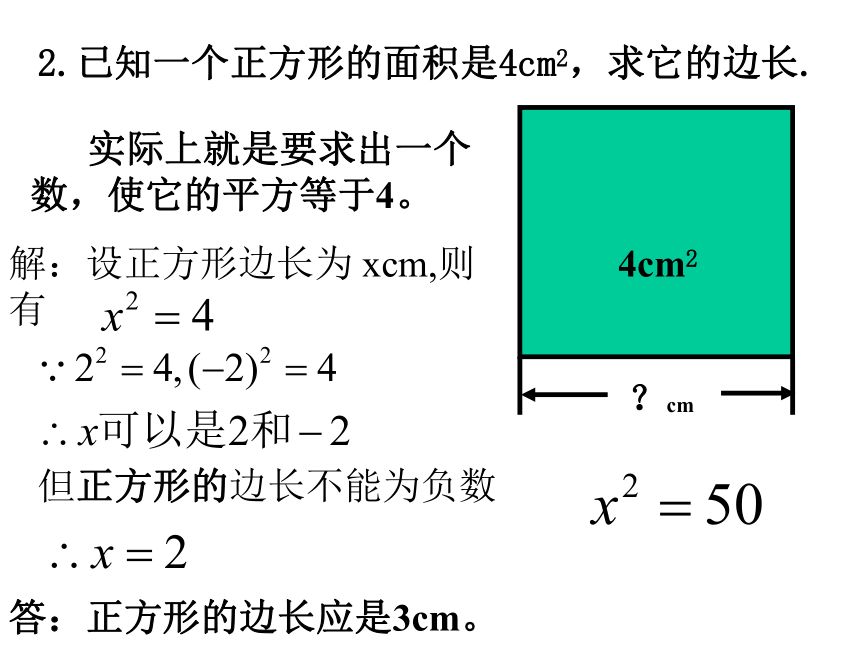
2.已知一个正方形的面积是4cm2,求它的边长.
1.一个正方形桌面的边长是3尺,求这个桌面的面积是多少平方尺?这个问题实际上就是求:答:9平方尺这是已知底数和指数,求幂的运算乘方运算2.已知一个正方形的面积是4cm2,求它的边长. 实际上就是要求出一个数,使它的平方等于4。答:正方形的边长应是3cm。4cm2解:设正方形边长为 xcm,则有但正方形的边长不能为负数填空:
(1)32=( ),(-3)2=( ),
22=( ),(-2)2=( ) 02=( )99440 如果一个数的平方等于a,这个数叫做a的平方根(也叫做二次方根) 如:22=4,2是4的平方根;(一2)2=4,(一2)也是4的平方根.即 4的平方根是±2. 练习:1、请分别说出49, ,0的平方根.
2、-4有没有平方根,为什么?
一个正数有正、负两个平方根,它们互为相反数;零的平方根是零;负数没有平方根. 思考:是不是每个数有平方根?如果有的话,有几个?它们之间有什么关系?让学生自学课文中间部分的内容,并完成下列问题:
试一试
(1)正数a的正的平方根用符号( )表示.读作___________
(2)正数a的负的平方根用符号( )表示.读作________
(3)正数a的平方根用符号( )表示。读作____________.
(4)x2= a 中,x 叫___,2 叫______; 中,2叫______,a 叫_____
(5) 中的a 应是_________数,能是负数吗? 一个正数a的正平方根,用“ ”表示,读作“根号a”,“ ”是“2 ”的简写.根指数“2”省略不写;
它的负平方根,用“- ”表示,读作“负根号a”.
合起来,一个正数a的平方根就用“± ”表示,读作正、负根号a,其中a叫做被开方数.如4的平方根记做± 练习:1.用正确的符号表示下列各数的平方根: ①26? ②247? ③0.2? ④3? ⑤求一个数的平方根的运算叫做开平方. 例1 求下列各数的平方根:
(l)9 (2)0.36 (3) (4)
解: (1)∴9的平方根是±3请你妨照上面的例子完成其余三个小题。想一想 “负数没有平方根”与“一个数的平方根不能为负数”意义是否一样? 求一个数的平方根(二次方根)的运算,叫做开平方,开平方运算的结果就是平方根。当然,平方和开平方互为逆运算。判断正误,并且改错:
(l)100的平方根是10;
(2)非负数(正数和零统称非负数)一定有2个平方根;
(3)
(4)2的平方根是± .
例2:判断下列各数有没有平方根,如果有平方根,试求出它的平方根;如果没有平方根,说明理由。(1)81(2)-81(3)0 (4) (5) 注意:因为负数没有平方根,所以在式子
中的被开方数 a ≥0 ,否则式子 没有意义。即式子 中的 a 是一个非负数。
(1)如果一个数的平方等于a,这个数叫做a的平方根;
(2)正数a的平方根有两个,它们互为相反数,零的平方根是零,负数没有平方根;
(3)求一个数的平方根的运算叫做开平方,平方和开平方互为逆运算.
谈谈你的收获1、知识方面:这节课我们学习了平方根的概念、表 示方法、求法及平方根的性质。
2、思维方法:平方运算和开平方运算互为逆运算,可以互相检验。
3、探究策略:由特殊到一般,再由一般到特殊,是发现问题和解决问题的基本方法和途径。
4、用定义解决问题也是的常用方法和有力工具。
本节课你学习了哪些知识?在 探索知识的过程中,你用了哪些方法?对你今后的学习有什么帮助?
2.已知一个正方形的面积是4cm2,求它的边长.
1.一个正方形桌面的边长是3尺,求这个桌面的面积是多少平方尺?这个问题实际上就是求:答:9平方尺这是已知底数和指数,求幂的运算乘方运算2.已知一个正方形的面积是4cm2,求它的边长. 实际上就是要求出一个数,使它的平方等于4。答:正方形的边长应是3cm。4cm2解:设正方形边长为 xcm,则有但正方形的边长不能为负数填空:
(1)32=( ),(-3)2=( ),
22=( ),(-2)2=( ) 02=( )99440 如果一个数的平方等于a,这个数叫做a的平方根(也叫做二次方根) 如:22=4,2是4的平方根;(一2)2=4,(一2)也是4的平方根.即 4的平方根是±2. 练习:1、请分别说出49, ,0的平方根.
2、-4有没有平方根,为什么?
一个正数有正、负两个平方根,它们互为相反数;零的平方根是零;负数没有平方根. 思考:是不是每个数有平方根?如果有的话,有几个?它们之间有什么关系?让学生自学课文中间部分的内容,并完成下列问题:
试一试
(1)正数a的正的平方根用符号( )表示.读作___________
(2)正数a的负的平方根用符号( )表示.读作________
(3)正数a的平方根用符号( )表示。读作____________.
(4)x2= a 中,x 叫___,2 叫______; 中,2叫______,a 叫_____
(5) 中的a 应是_________数,能是负数吗? 一个正数a的正平方根,用“ ”表示,读作“根号a”,“ ”是“2 ”的简写.根指数“2”省略不写;
它的负平方根,用“- ”表示,读作“负根号a”.
合起来,一个正数a的平方根就用“± ”表示,读作正、负根号a,其中a叫做被开方数.如4的平方根记做± 练习:1.用正确的符号表示下列各数的平方根: ①26? ②247? ③0.2? ④3? ⑤求一个数的平方根的运算叫做开平方. 例1 求下列各数的平方根:
(l)9 (2)0.36 (3) (4)
解: (1)∴9的平方根是±3请你妨照上面的例子完成其余三个小题。想一想 “负数没有平方根”与“一个数的平方根不能为负数”意义是否一样? 求一个数的平方根(二次方根)的运算,叫做开平方,开平方运算的结果就是平方根。当然,平方和开平方互为逆运算。判断正误,并且改错:
(l)100的平方根是10;
(2)非负数(正数和零统称非负数)一定有2个平方根;
(3)
(4)2的平方根是± .
例2:判断下列各数有没有平方根,如果有平方根,试求出它的平方根;如果没有平方根,说明理由。(1)81(2)-81(3)0 (4) (5) 注意:因为负数没有平方根,所以在式子
中的被开方数 a ≥0 ,否则式子 没有意义。即式子 中的 a 是一个非负数。
(1)如果一个数的平方等于a,这个数叫做a的平方根;
(2)正数a的平方根有两个,它们互为相反数,零的平方根是零,负数没有平方根;
(3)求一个数的平方根的运算叫做开平方,平方和开平方互为逆运算.
谈谈你的收获1、知识方面:这节课我们学习了平方根的概念、表 示方法、求法及平方根的性质。
2、思维方法:平方运算和开平方运算互为逆运算,可以互相检验。
3、探究策略:由特殊到一般,再由一般到特殊,是发现问题和解决问题的基本方法和途径。
4、用定义解决问题也是的常用方法和有力工具。
本节课你学习了哪些知识?在 探索知识的过程中,你用了哪些方法?对你今后的学习有什么帮助?
