6.2立方根(第一课时)课件_人教新课标版
文档属性
| 名称 | 6.2立方根(第一课时)课件_人教新课标版 |  | |
| 格式 | zip | ||
| 文件大小 | 650.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-25 10:23:26 | ||
图片预览







文档简介
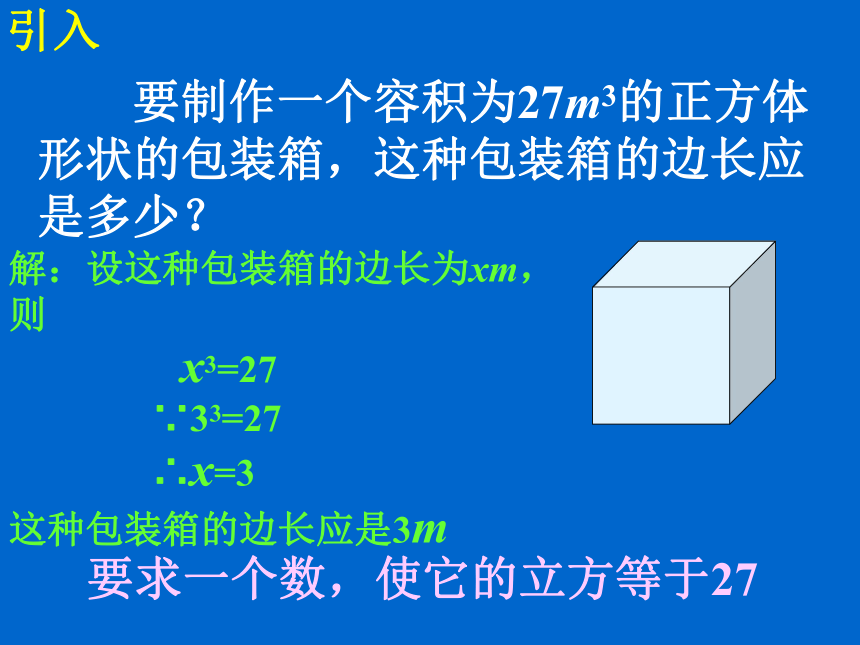
课件25张PPT。第六章 实数 立方根第1课时引入 要制作一个容积为27m3的正方体
形状的包装箱,这种包装箱的边长应
是多少?解:设这种包装箱的边长为xm,则
x3=27
∵33=27
∴x=3
这种包装箱的边长应是3m要求一个数,使它的立方等于27探究(1) ( )3=8; (2) ( )3= -8;
(3) ( )3= ; (4) ( )3= ;立方根的定义:如果x3=a , 那么x就叫做a的立方根(三次方根). a叫做x的三次幂。归纳开立方的定义:求一个数a的立方根的
运算,叫做开立方.如:3是27的立方根∴27的立方根是3如果 ,那么 。如何表示一个数的立方根?一个数a的立方根可以表示为:读作:三次根号 a
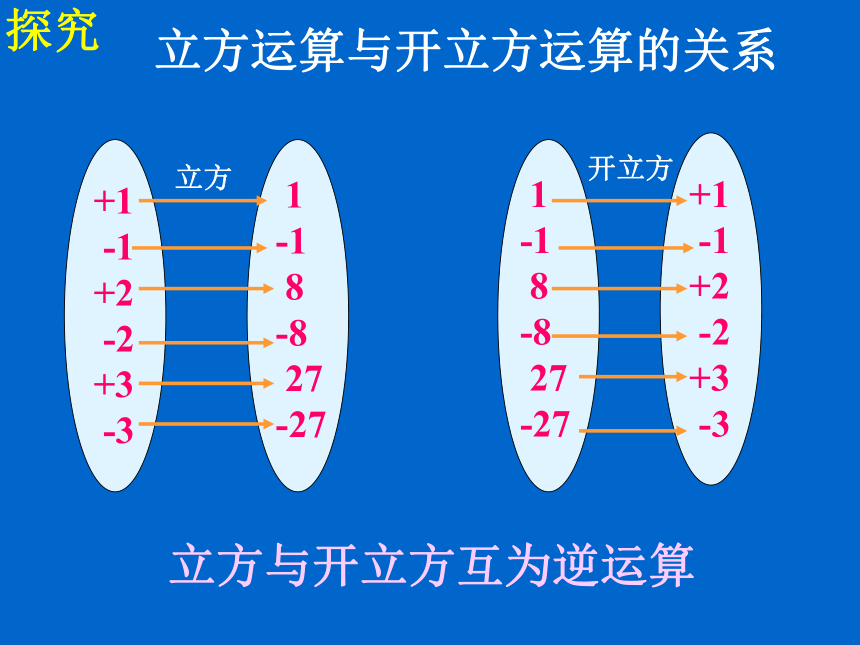
其中a是被开方数,3是根指数,不能省略。a3被开方数探究 1
-1
8
-8
27
-27立方开立方立方运算与开立方运算的关系立方与开立方互为逆运算 1
-1
8
-8
27
-27归纳立方根的表示方法:如果x3=a ,那么x = .探究1、正数的立方根是正数,
2、负数的立方根是负数;
3、0的立方根是0; 例2:求下列各式的值。解:(1)(2)(3)方法点拨:先定符号,再定值。 例2:求下列各式的值。解:(4)(5)
(1)1的平方根是____;立方根为____;算术平方根为_ _.
(2)平方根是它本身的数是____
(3)立方根是其本身的数是____
(4)算术平方根是其本身的数是____.(5) 的立方根为 . (6) 的平方根为 . (7) 的立方根为 . 填空练习:±11 100,1,-10,1-2±2-8范例例2、求下列方程:方法:
1、把x3当作一个整体,求出x3=a;
2、再根据立方根的定义求x.巩固求下列方程:1. 判断正误:
(1)、25的立方根是 5 ;( )
(2)、互为相反数的两个数,它们的立方根也互为相反数;( )
(3)、任何数的立方根只有一个;( )
(4)、如果一个数的平方根与其立方根相同,则 这个数是1;( )
(5)、如果一个数的立方根是这个数的本身,那么这个数一定是零;( )
(6)、一个数的立方根不是正数就是负数.( )
(7)、–64没有立方根.( ) √√√××××检测2、填空:(1) 的立方根是 ;(2) 的立方根是 ;53、填空:(1) 的立方根是 ;(2) 的立方根是 ;6-6
(1)1的平方根是____;立方根为____;算术平方根为_ _.
(2)平方根是它本身的数是____
(3)立方根是其本身的数是____
(4)算术平方根是其本身的数是____.(5) 的立方根为 . (6) 的平方根为 . (7) 的立方根为 . 填空练习:±11 100,1,-10,1-2±2-81、下列等式正确的是( )
A B
C D检测 D3、若一个数的立方根和它的算术平方
根相等,则这个数是( )
A.1 B. 0
C.0或1 D. 1、0或-1检测 C3、若一个数的立方根和它的算术平方
根相等,则这个数是( )
A.1 B. 0
C.0或1 D. 1、0或-1检测 C1、已知x-2的平方根是,的立方根是4,求的值.
2 、思考:一个正方体的体积变为原来的n倍,它的棱长变为原来的多少倍? 如果一个数X的立方等于a,即X3=a,那么,这个数X就叫做a的立方根。 ∵ (-2)3=-8,
∴ -2是-8的立方根。二、比对:
1、立方根的定义:2、立方根的性质与表示 每个数都只有一个立方根。正数的立方根是正数;0的立方根是0;负数的立方根是负数。3、开立方求一个数a的立方根的运算,叫做开立方。 ①它与立方互为逆运算;
②它是一种运算,而不是结果,它的结果是立方根。小结1、本节课你学了什么知识?2、你有什么体会?立方根的定义立方根的表示求一个数的立方根的方法立方根与平方根的区别、联系
形状的包装箱,这种包装箱的边长应
是多少?解:设这种包装箱的边长为xm,则
x3=27
∵33=27
∴x=3
这种包装箱的边长应是3m要求一个数,使它的立方等于27探究(1) ( )3=8; (2) ( )3= -8;
(3) ( )3= ; (4) ( )3= ;立方根的定义:如果x3=a , 那么x就叫做a的立方根(三次方根). a叫做x的三次幂。归纳开立方的定义:求一个数a的立方根的
运算,叫做开立方.如:3是27的立方根∴27的立方根是3如果 ,那么 。如何表示一个数的立方根?一个数a的立方根可以表示为:读作:三次根号 a
其中a是被开方数,3是根指数,不能省略。a3被开方数探究 1
-1
8
-8
27
-27立方开立方立方运算与开立方运算的关系立方与开立方互为逆运算 1
-1
8
-8
27
-27归纳立方根的表示方法:如果x3=a ,那么x = .探究1、正数的立方根是正数,
2、负数的立方根是负数;
3、0的立方根是0; 例2:求下列各式的值。解:(1)(2)(3)方法点拨:先定符号,再定值。 例2:求下列各式的值。解:(4)(5)
(1)1的平方根是____;立方根为____;算术平方根为_ _.
(2)平方根是它本身的数是____
(3)立方根是其本身的数是____
(4)算术平方根是其本身的数是____.(5) 的立方根为 . (6) 的平方根为 . (7) 的立方根为 . 填空练习:±11 100,1,-10,1-2±2-8范例例2、求下列方程:方法:
1、把x3当作一个整体,求出x3=a;
2、再根据立方根的定义求x.巩固求下列方程:1. 判断正误:
(1)、25的立方根是 5 ;( )
(2)、互为相反数的两个数,它们的立方根也互为相反数;( )
(3)、任何数的立方根只有一个;( )
(4)、如果一个数的平方根与其立方根相同,则 这个数是1;( )
(5)、如果一个数的立方根是这个数的本身,那么这个数一定是零;( )
(6)、一个数的立方根不是正数就是负数.( )
(7)、–64没有立方根.( ) √√√××××检测2、填空:(1) 的立方根是 ;(2) 的立方根是 ;53、填空:(1) 的立方根是 ;(2) 的立方根是 ;6-6
(1)1的平方根是____;立方根为____;算术平方根为_ _.
(2)平方根是它本身的数是____
(3)立方根是其本身的数是____
(4)算术平方根是其本身的数是____.(5) 的立方根为 . (6) 的平方根为 . (7) 的立方根为 . 填空练习:±11 100,1,-10,1-2±2-81、下列等式正确的是( )
A B
C D检测 D3、若一个数的立方根和它的算术平方
根相等,则这个数是( )
A.1 B. 0
C.0或1 D. 1、0或-1检测 C3、若一个数的立方根和它的算术平方
根相等,则这个数是( )
A.1 B. 0
C.0或1 D. 1、0或-1检测 C1、已知x-2的平方根是,的立方根是4,求的值.
2 、思考:一个正方体的体积变为原来的n倍,它的棱长变为原来的多少倍? 如果一个数X的立方等于a,即X3=a,那么,这个数X就叫做a的立方根。 ∵ (-2)3=-8,
∴ -2是-8的立方根。二、比对:
1、立方根的定义:2、立方根的性质与表示 每个数都只有一个立方根。正数的立方根是正数;0的立方根是0;负数的立方根是负数。3、开立方求一个数a的立方根的运算,叫做开立方。 ①它与立方互为逆运算;
②它是一种运算,而不是结果,它的结果是立方根。小结1、本节课你学了什么知识?2、你有什么体会?立方根的定义立方根的表示求一个数的立方根的方法立方根与平方根的区别、联系
