数的开方复习课[上学期]
图片预览








文档简介
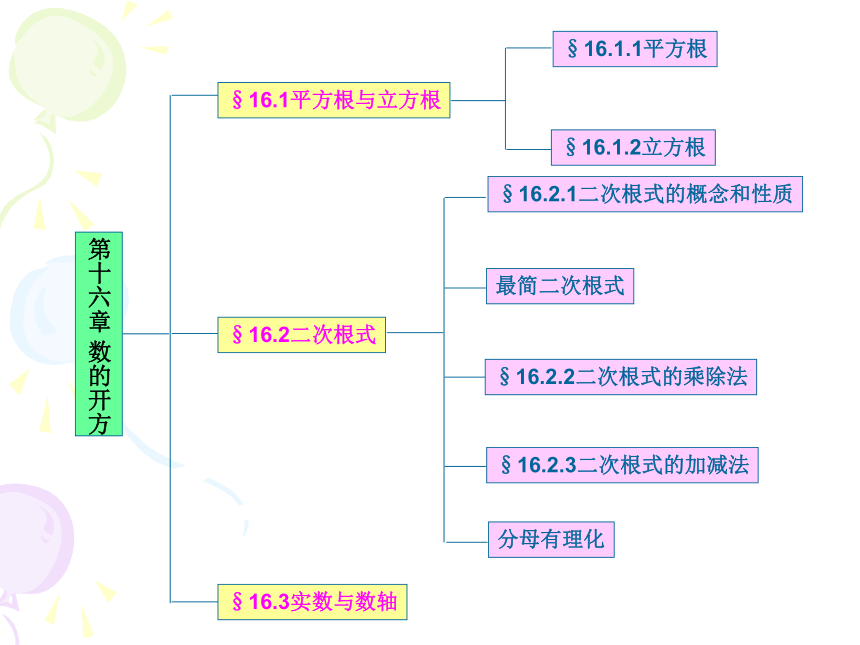
课件21张PPT。第十六章 数的开方§16.1平方根与立方根§16.2二次根式§16.3实数与数轴§16.2.1二次根式的概念和性质最简二次根式§16.2.2二次根式的乘除法§16.2.3二次根式的加减法§16.1.1平方根§16.1.2立方根分母有理化16.1 平方根与立方根如果一个数的平方等于a,2、平方根的性质:
*一个正数有( )个平方根,且它们( );
*零只有( )个平方根;
*负数( )。2互为相反数1没有平方根正数a的正的平方根注:0的算术平方根是0。一、平方根4、开平方
叫做开平方。
其关键是 。求一个非负数的平方根的运算找出它的算术平方根互为逆运算 1、立方根的概念
一般地,如果一个数x的立方等于a,即x3=a,那么这个数x就叫做a的立方根. 表示方法 数a的立方根用符号 表示,读作“三次根号a”,其中a是被开方数,3是根指数. 2、开立方
——求一个数的立方根的运算.二、立方根立方与开立方互为逆运算.3、立方根的性质
性质一:正数的立方根只有一个,仍是正数;
0的立方根就是0;
负数的立方根只有一个,仍是负数.性质二性质三 也就是可以把根号里的“负号”直接从根号里面提 到了根号“外面” 。二次根式的基本性质(一)二次根式的特征: (1)含有二次根号(2)被开方数(或式)必须非负(双重非负性)16.2 二次根式二次根式.2、1、思维体操0或102c满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数中的因数是整数,因式是整式;
(2)被开方数中不含能开得尽方的因数或因式;
(3)分母中不含根号。最简二次根式的定义3、最简二次根式(2) ( );(7) ( );判断下列各式是否为最简二次根式? (5) ( );(3) ( );(4) ( ); (1) ( );(6) ( );√×××××√辨析训练 议一议:
如果最简根式 与 是同类二次根式,求ab的值.分析:最简二次根式是同类二次根式,所以根指数都等于2,被开方数相同,列二元一次方程组.解:由题意,得
2a-b=2
a+5=9-b,所以ab=4.4、二次根式的四则运算(1)、乘法的运算法则:(2)、除法的运算法则: 商的算术平方根:
①数学表达式:
②语言叙述:商的算术平方根等于被除式的算术平方根除以除式的算术平方根。注意:
如果被开方数是带分数,应先化成假分数。解:商的算术平方根的性质的应用
例1:化简下列各式(以前课堂上做过的题,你现在觉得很简单了吧?)
二次根式的除法公式的应用:例2. 计算:
解:如果根号前有系数,就把系数相除,仍旧作为二
次根号前的系数。①同类二次根式判断是否为同类二次根式的步骤是什么?(1)化成最简二次根式;
(2)看被开方数是否相同;
(3)看根指数是否相同(都等于2).几个二次根式化成最简二次根式后,如果被开方数相同,那么这几个二次根式就叫做同类二次根式.(3)、加减法的运算法则:②如何合并同类二次根式与合并同类项类似,把同类二次根式的系数相加减,做为结果的系数,根号及根号内部都不变.③二次根式加减运算的步骤:(1)把各个二次根式化成最简二次根式
(2)把各个同类二次根式合并.5、分母有理化的概念:
把分母中的根号化去,使分母变成有理数,这个过程叫做分母有理化。
看看我们曾经做过的题目例5:化简返回 1. 叫做无理数.16.3 实数和数轴无限不循环小数注意:(2)无理数不一定都是用根号表示的数.如:π (3)无理数有无数多个.(4)无理数可分为正无理数和负无理数.(1)用根号表示的数不一定是无理数.如:(5)请同学们试着记忆以下无理数的近似值,它们将会给我们将来的计算带来很多便利:2、4、每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数。即:统称实数.有理数和无理数3、实数如何分类?实数和数轴上的点是一 一对应的.乘法交换律:ab=ba
乘法结合律:(ab)c=a(bc)
乘法分配律:a(b+c)=ab+ac
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
平方差公式:(a+b)(a-b)=a2-b2
完全平方公式:(a±b)2= a2±2ab+b2
相反数:a —— -a
倒数:a ——
a(a≥0)
绝对值:a —— |a|=
-a(a<0)5、有理数范围中成立,
在实数范围
中同样成立答案:(1)2(2)- 6(4)3练习拓展1、按从小到大的顺序排序:
2、计算并将结果化简:
*一个正数有( )个平方根,且它们( );
*零只有( )个平方根;
*负数( )。2互为相反数1没有平方根正数a的正的平方根注:0的算术平方根是0。一、平方根4、开平方
叫做开平方。
其关键是 。求一个非负数的平方根的运算找出它的算术平方根互为逆运算 1、立方根的概念
一般地,如果一个数x的立方等于a,即x3=a,那么这个数x就叫做a的立方根. 表示方法 数a的立方根用符号 表示,读作“三次根号a”,其中a是被开方数,3是根指数. 2、开立方
——求一个数的立方根的运算.二、立方根立方与开立方互为逆运算.3、立方根的性质
性质一:正数的立方根只有一个,仍是正数;
0的立方根就是0;
负数的立方根只有一个,仍是负数.性质二性质三 也就是可以把根号里的“负号”直接从根号里面提 到了根号“外面” 。二次根式的基本性质(一)二次根式的特征: (1)含有二次根号(2)被开方数(或式)必须非负(双重非负性)16.2 二次根式二次根式.2、1、思维体操0或102c满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数中的因数是整数,因式是整式;
(2)被开方数中不含能开得尽方的因数或因式;
(3)分母中不含根号。最简二次根式的定义3、最简二次根式(2) ( );(7) ( );判断下列各式是否为最简二次根式? (5) ( );(3) ( );(4) ( ); (1) ( );(6) ( );√×××××√辨析训练 议一议:
如果最简根式 与 是同类二次根式,求ab的值.分析:最简二次根式是同类二次根式,所以根指数都等于2,被开方数相同,列二元一次方程组.解:由题意,得
2a-b=2
a+5=9-b,所以ab=4.4、二次根式的四则运算(1)、乘法的运算法则:(2)、除法的运算法则: 商的算术平方根:
①数学表达式:
②语言叙述:商的算术平方根等于被除式的算术平方根除以除式的算术平方根。注意:
如果被开方数是带分数,应先化成假分数。解:商的算术平方根的性质的应用
例1:化简下列各式(以前课堂上做过的题,你现在觉得很简单了吧?)
二次根式的除法公式的应用:例2. 计算:
解:如果根号前有系数,就把系数相除,仍旧作为二
次根号前的系数。①同类二次根式判断是否为同类二次根式的步骤是什么?(1)化成最简二次根式;
(2)看被开方数是否相同;
(3)看根指数是否相同(都等于2).几个二次根式化成最简二次根式后,如果被开方数相同,那么这几个二次根式就叫做同类二次根式.(3)、加减法的运算法则:②如何合并同类二次根式与合并同类项类似,把同类二次根式的系数相加减,做为结果的系数,根号及根号内部都不变.③二次根式加减运算的步骤:(1)把各个二次根式化成最简二次根式
(2)把各个同类二次根式合并.5、分母有理化的概念:
把分母中的根号化去,使分母变成有理数,这个过程叫做分母有理化。
看看我们曾经做过的题目例5:化简返回 1. 叫做无理数.16.3 实数和数轴无限不循环小数注意:(2)无理数不一定都是用根号表示的数.如:π (3)无理数有无数多个.(4)无理数可分为正无理数和负无理数.(1)用根号表示的数不一定是无理数.如:(5)请同学们试着记忆以下无理数的近似值,它们将会给我们将来的计算带来很多便利:2、4、每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数。即:统称实数.有理数和无理数3、实数如何分类?实数和数轴上的点是一 一对应的.乘法交换律:ab=ba
乘法结合律:(ab)c=a(bc)
乘法分配律:a(b+c)=ab+ac
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
平方差公式:(a+b)(a-b)=a2-b2
完全平方公式:(a±b)2= a2±2ab+b2
相反数:a —— -a
倒数:a ——
a(a≥0)
绝对值:a —— |a|=
-a(a<0)5、有理数范围中成立,
在实数范围
中同样成立答案:(1)2(2)- 6(4)3练习拓展1、按从小到大的顺序排序:
2、计算并将结果化简:
