北京四中2022~2023学年九年级下数学统练(pdf、无答案)
文档属性
| 名称 | 北京四中2022~2023学年九年级下数学统练(pdf、无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-17 09:23:17 | ||
图片预览


文档简介
数学练习 3(3 月 14 日)
班级: 姓名: 成绩:
一. 选择题
1. 自 2019 年底, 由新型冠状病毒 SARS-Cov-2 引发的新冠肺炎席卷全球, 截止 2020 年
4 月 10 日, 全球共有 185 个国家或地区报告发现了确诊者, 累积确诊约 1600000 人.
将 1600000 用科学记数法表示应为( )
A. 160 万 B. 160 × 10 C. 1.6 × 10 D. 1.6 × 10
2. 如图是某个几何体的三视图, 该几何体是( )
A. 圆锥 B. 四棱锥
C. 圆柱 D. 四棱柱
3. 实数 a,b,c,d 在数轴上的对应点的位置如图所示.
若 + = 0,则下列结论中正确的是( )
A. + > 0 B. > 1 C. > D. | | > | |
4. 如果 + 2 2 = 0, 那么代数式( + ) 的值是( )
A. 2 B. 1 C. 2 D. 3
5. 若正多边形的一个外角是40°, 则这个正多边形是( )
A. 正七边形 B. 正八边形 C. 正九边形 D. 正十边形
6. 如图, 点 A, B, C 在⊙ 上, CO 的延长线交 AB 于点 D,
∠ = 50°, ∠ = 30°, 则∠ 的度数为( )
A. 70° B. 90°
C. 110° D. 120°
7. 定点投篮是同学们喜爱的体育项目之一, 某位同学投出篮球的飞行路线可以看作是
抛物线的一部分, 篮球飞行的竖直高度 (单位: m)与水平距离 (单位: m)近似满足
函数关系 = + + ( ≠ 0). 下表记录了该同学将篮球投出后的 x 与 y 的三
组数据, 根据上述函数模型和数据, 可推断出篮球飞行到最高点时, 水平距离为( )
A. 1.5m B. 2m C. 2.5m D. 3m
第 1页 /共 8页
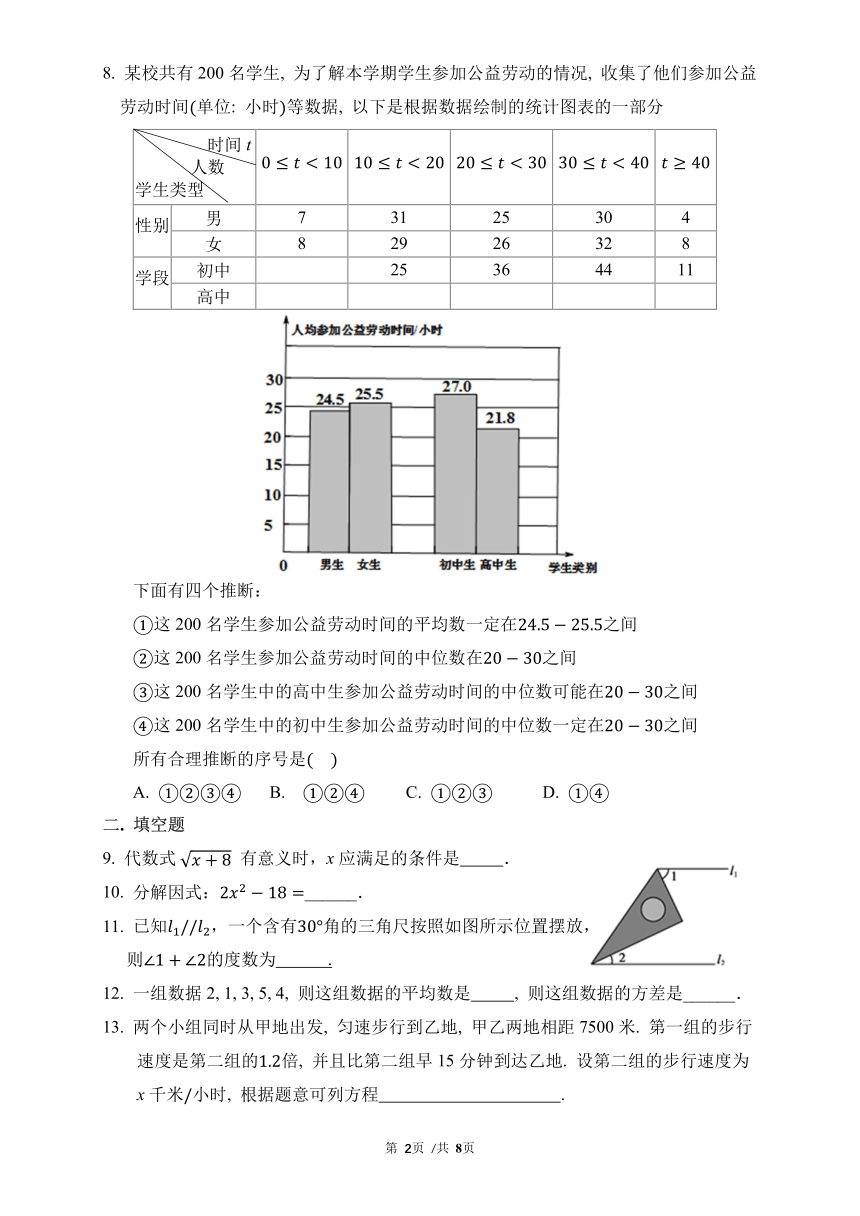
8. 某校共有 200 名学生, 为了解本学期学生参加公益劳动的情况, 收集了他们参加公益
劳动时间(单位: 小时)等数据, 以下是根据数据绘制的统计图表的一部分
时间 t
人数 0 ≤ < 10 10 ≤ < 20 20 ≤ < 30 30 ≤ < 40 ≥ 40
学生类型
性别 男 7 31 25 30 4
女 8 29 26 32 8
初中 25 36 44 11 学段
高中
下面有四个推断:
①这 200 名学生参加公益劳动时间的平均数一定在24.5 25.5之间
②这 200 名学生参加公益劳动时间的中位数在20 30之间
③这 200 名学生中的高中生参加公益劳动时间的中位数可能在20 30之间
④这 200 名学生中的初中生参加公益劳动时间的中位数一定在20 30之间
所有合理推断的序号是( )
A. ①②③④ B. ①②④ C. ①②③ D. ①④
二. 填空题
9. 代数式 √ + 8 有意义时,x 应满足的条件是 .
10. 分解因式:2 18 =______.
11. 已知 // ,一个含有30°角的三角尺按照如图所示位置摆放,
则∠1 + ∠2的度数为 .
12. 一组数据 2, 1, 3, 5, 4, 则这组数据的平均数是 , 则这组数据的方差是______.
13. 两个小组同时从甲地出发, 匀速步行到乙地, 甲乙两地相距 7500 米. 第一组的步行
速度是第二组的1.2倍, 并且比第二组早 15 分钟到达乙地. 设第二组的步行速度为
x 千米/小时, 根据题意可列方程 .
第 2页 /共 8页
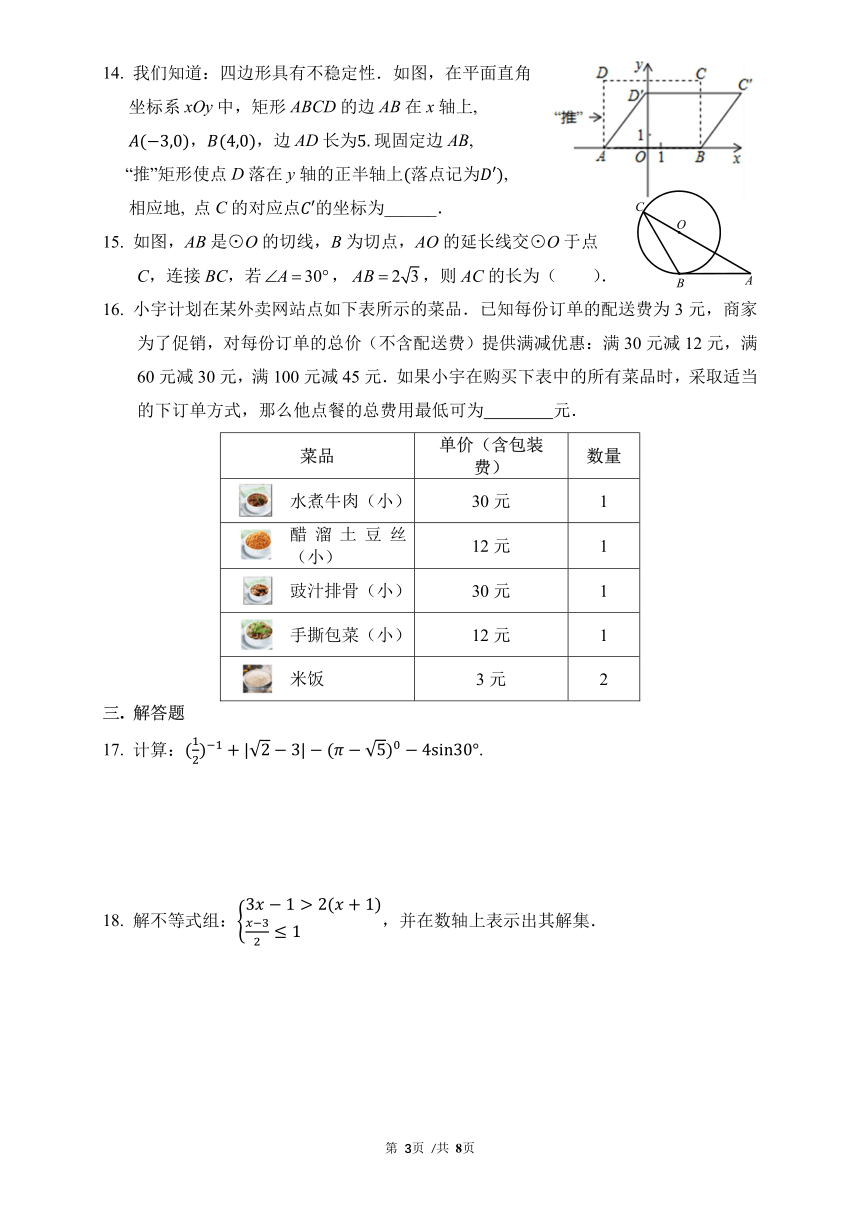
14. 我们知道:四边形具有不稳定性.如图,在平面直角
坐标系 xOy 中,矩形 ABCD 的边 AB 在 x 轴上,
( 3,0), (4,0),边 AD 长为5. 现固定边 AB,
“推”矩形使点 D 落在 y 轴的正半轴上(落点记为 ′),
相应地, 点 C 的对应点 ′的坐标为______. C
O
15. 如图,AB 是⊙O 的切线,B 为切点,AO 的延长线交⊙O 于点
C,连接 BC,若 A 30 , AB 2 3,则 AC 的长为( ). B A
16. 小宇计划在某外卖网站点如下表所示的菜品.已知每份订单的配送费为 3 元,商家
为了促销,对每份订单的总价(不含配送费)提供满减优惠:满 30 元减 12 元,满
60 元减 30 元,满 100 元减 45 元.如果小宇在购买下表中的所有菜品时,采取适当
的下订单方式,那么他点餐的总费用最低可为 元.
单价(含包装
菜品 数量
费)
水煮牛肉(小) 30 元 1
醋 溜 土 豆 丝
12 元 1
(小)
豉汁排骨(小) 30 元 1
手撕包菜(小) 12 元 1
米饭 3 元 2
三. 解答题
17. 计算:( ) + |√2 3| ( √5) 4sin30°.
3 1 > 2( + 1)
18. 解不等式组: ,并在数轴上表示出其解集.
≤ 1
第 3页 /共 8页
19. 已知关于 x 的一元二次方程 ( 2) + 2 + + 3 = 0 有两个不相等实数根.
(1) 求 m 的取值范围;
(2) 当 m 取满足条件的最大整数时, 求方程的根.
20. 如图, 在□ABCD 中, = 2 . E, F 分别是 BC, AD 的中点, AE 和 BF 交于点 O,
连接 EF, OC.
(1)求证:四边形 ABEF 是菱形;
(2)若 = 8, ∠ = 60°, 求 OC 的长.
21. 北京世界园艺博览会(以下简称“世园会”)于 2019 年 4 月 29 日至 10 月 7 日在北京
市延庆区举行. 世园会为满足大家的游览需求, 倾情打造了 4 条各具特色的游玩路
线, 如下表:
A B C D
漫步世园会 爱家乡,爱园艺 清新园艺之旅 车览之旅
小美和小红都计划去世园会游玩,她们各自在这 4 条路线中任意选择一条,每条线
路被选择的可能性相同.
(1) 求小美选择路线“清新园艺之旅”的概率是多少?
(2) 用画树状图或列表的方法,求小美和小红恰好选择同一条路线的概率.
第 4页 /共 8页
22. 某商场销售一种进价为每件 10 元的日用商品, 经调查发现, 该商品每天的销售量
(件)与销售单价 (元)满足 = 10 + 400, 设销售这种商品每天的利润为 (元).
(1) 求 W 关于 x 的函数解析式;
(2) 在保证销售量尽可能大的前提下,若该商场每天想获得 2000 元的利润,应将销售
单价定为多少元
(3) 当每天销售量不少于 50 件,且销售单价至少为 32 元时,该商场每天获得的最大
利润是多少
23. 在平面直角坐标系 xOy 中,直线 = + ( < 0),经过点(6,0),且与坐标轴围
成的三角形的面积是 9,与函数 = ( > 0)的图象 G 交于 A,B 两点.
(1)求直线的表达式;
(2)横、纵坐标都是整数的点叫作整点.记图象 G 在点 A、B 之间的部分与线段 AB 围
成的区域(不含边界)为 W.
①当 = 2时,直接写出区域 W 内的整点的坐标______;
②若区域 W 内恰有 3 个整数点,结合函数图象,求 m 的取值范围.
第 5页 /共 8页
24. 如图, AB 是⊙O 的直径, 点 C 在⊙O 上, 点 P 是⊙O 上一动点, 且与点 C 分别位于
4
直径 AB 的两侧, tan∠CPB , 过点 C 作CQ⊥CP 交 PB 的延长线于点 Q;
3
(1) 当点 P 运动到什么位置时, CQ 恰好是⊙O 的切线?画出图形并加以说明。
(2) 若点 P 与点 C 关于直径 AB 对称, 且 AB=5, 画出图形求此时 CQ 的长.
C C
A B A B
O O
备用图
25. 如图, 在矩形 ABCD 中, E 是 BA 延长线上的定点,
M 为 BC 边上的一个动点, 连接 ME, 将射线 ME
绕点 M 顺时针旋转 76 , 交射线 CD 于点 F, 连接 MD.
小东根据学习函数的经验, 对线段 BM, DF, DM 的长度之间的关系进行了探究.
下面是小东探究的过程, 请补充完整:
(1) 对于点 M 在 BC 上的不同位置, 画图、测量, 得到了线段 BM, DF, DM 的长度的
几组值, 如下表:
位置 位置 位置 位置 位置 位置 位置 位置 位置
1 2 3 4 5 6 7 8 9
BM/cm 0.00 0.53 1.00 1.69 2.17 2.96 3.46 3.79. 4.00
DF/cm 0.00 1.00 1.74 2.49 2.69 2.21 1.14 0.00 1.00
DM/cm 4.12 3.61 3.16 2.52 2.09 1.44 1.14 1.02 1.00
第 6页 /共 8页
在 BM, DF, DM 的长度这三个量中, 确定
的长度是自变量, 的长度
和 的长度都是这个自变量的函数;
(2) 在同一平面直角坐标系 xOy 中, 画出 (1)
中所确定的两个函数的图象;
(3) 结合画出的函数图象, 解决问题: 当
DF=2cm 时, DM 的长度约为 cm.
26. 在平面直角坐标系 xOy 中, 有抛物线 = 3 4 + 3 和直线 y=3x+6.
其中, 直线与 x 轴, y 轴分别交于点 A, B. 将点 B 向右平移 6 个单位长度, 得到点 C.
(1) 求点 C 的坐标和抛物线的对称轴;
(2) 若抛物线与折线段 A-B-C 恰有两个公共点, 结合函数图象, 求 m 的取值范围.
27. 在△ 中, ∠ = 120°, = , = √3 , 设∠ = , ∠ = .
(1)如图 1, 当点 P 在△ 内,
① 若 = 153°, 求 的度数;
小明同学通过分析已知条件发现: △ 是顶角为120°的等腰三角形, 且 = √3 ,
从而容易联想到构造一个顶角为120°的等腰三角形. 于是, 他过点 A 作∠DAP=120°,
且 = , 连接 DP, DB, 发现两个不同的三角形全等: ≌ , 再利用全
等三角形及等腰三角形的相关知识可求出 的度数.
请利用小王同学分析的思路, 通过计算求得 的度数为______;
② 小王在①的基础上进一步进行探索, 发现 、 之间存在一种特殊的等量关系, 请写
出这个等量关系, 并加以证明.
第 7页 /共 8页
(2)如图 2, 点 P 在△ 外, 那么 、 之间的数量关系是否改变 若改变, 请直接写出
P
它们的数量关系; 若不变, 请说明理由.
A
D
AP
B C
B C
图 1 图 2
28. 对于平面直角坐标系 xOy 上的点 P 和⊙C, 定义如下: 若⊙C 上存在两个点 A, B,
使得点 P 在射线 BC 上, 且∠ = ∠ (0° < ∠ < 180°), 则称 P 为⊙C 的依附
点.
(1) 当⊙O 的半径为 1 时
① 已知点 ( 2.5,0), (0, 2), (1,0), 在点 D, E, F 中, ⊙O 的依附点是______;
② 点 T 在直线 = 上, 若 T 为⊙O 的依附点, 求点 T 的横坐标 t 的取值范围;
(2) ⊙C 的圆心在 x 轴上, 半径为 1,直线 = 2 + 2与 x 轴、y 轴分别交于点 M、N,
若线段 MN 上的所有点都是⊙C 的依附点, 请求出圆心 C 的横坐标 的取值范围.
第 8页 /共 8页
班级: 姓名: 成绩:
一. 选择题
1. 自 2019 年底, 由新型冠状病毒 SARS-Cov-2 引发的新冠肺炎席卷全球, 截止 2020 年
4 月 10 日, 全球共有 185 个国家或地区报告发现了确诊者, 累积确诊约 1600000 人.
将 1600000 用科学记数法表示应为( )
A. 160 万 B. 160 × 10 C. 1.6 × 10 D. 1.6 × 10
2. 如图是某个几何体的三视图, 该几何体是( )
A. 圆锥 B. 四棱锥
C. 圆柱 D. 四棱柱
3. 实数 a,b,c,d 在数轴上的对应点的位置如图所示.
若 + = 0,则下列结论中正确的是( )
A. + > 0 B. > 1 C. > D. | | > | |
4. 如果 + 2 2 = 0, 那么代数式( + ) 的值是( )
A. 2 B. 1 C. 2 D. 3
5. 若正多边形的一个外角是40°, 则这个正多边形是( )
A. 正七边形 B. 正八边形 C. 正九边形 D. 正十边形
6. 如图, 点 A, B, C 在⊙ 上, CO 的延长线交 AB 于点 D,
∠ = 50°, ∠ = 30°, 则∠ 的度数为( )
A. 70° B. 90°
C. 110° D. 120°
7. 定点投篮是同学们喜爱的体育项目之一, 某位同学投出篮球的飞行路线可以看作是
抛物线的一部分, 篮球飞行的竖直高度 (单位: m)与水平距离 (单位: m)近似满足
函数关系 = + + ( ≠ 0). 下表记录了该同学将篮球投出后的 x 与 y 的三
组数据, 根据上述函数模型和数据, 可推断出篮球飞行到最高点时, 水平距离为( )
A. 1.5m B. 2m C. 2.5m D. 3m
第 1页 /共 8页
8. 某校共有 200 名学生, 为了解本学期学生参加公益劳动的情况, 收集了他们参加公益
劳动时间(单位: 小时)等数据, 以下是根据数据绘制的统计图表的一部分
时间 t
人数 0 ≤ < 10 10 ≤ < 20 20 ≤ < 30 30 ≤ < 40 ≥ 40
学生类型
性别 男 7 31 25 30 4
女 8 29 26 32 8
初中 25 36 44 11 学段
高中
下面有四个推断:
①这 200 名学生参加公益劳动时间的平均数一定在24.5 25.5之间
②这 200 名学生参加公益劳动时间的中位数在20 30之间
③这 200 名学生中的高中生参加公益劳动时间的中位数可能在20 30之间
④这 200 名学生中的初中生参加公益劳动时间的中位数一定在20 30之间
所有合理推断的序号是( )
A. ①②③④ B. ①②④ C. ①②③ D. ①④
二. 填空题
9. 代数式 √ + 8 有意义时,x 应满足的条件是 .
10. 分解因式:2 18 =______.
11. 已知 // ,一个含有30°角的三角尺按照如图所示位置摆放,
则∠1 + ∠2的度数为 .
12. 一组数据 2, 1, 3, 5, 4, 则这组数据的平均数是 , 则这组数据的方差是______.
13. 两个小组同时从甲地出发, 匀速步行到乙地, 甲乙两地相距 7500 米. 第一组的步行
速度是第二组的1.2倍, 并且比第二组早 15 分钟到达乙地. 设第二组的步行速度为
x 千米/小时, 根据题意可列方程 .
第 2页 /共 8页
14. 我们知道:四边形具有不稳定性.如图,在平面直角
坐标系 xOy 中,矩形 ABCD 的边 AB 在 x 轴上,
( 3,0), (4,0),边 AD 长为5. 现固定边 AB,
“推”矩形使点 D 落在 y 轴的正半轴上(落点记为 ′),
相应地, 点 C 的对应点 ′的坐标为______. C
O
15. 如图,AB 是⊙O 的切线,B 为切点,AO 的延长线交⊙O 于点
C,连接 BC,若 A 30 , AB 2 3,则 AC 的长为( ). B A
16. 小宇计划在某外卖网站点如下表所示的菜品.已知每份订单的配送费为 3 元,商家
为了促销,对每份订单的总价(不含配送费)提供满减优惠:满 30 元减 12 元,满
60 元减 30 元,满 100 元减 45 元.如果小宇在购买下表中的所有菜品时,采取适当
的下订单方式,那么他点餐的总费用最低可为 元.
单价(含包装
菜品 数量
费)
水煮牛肉(小) 30 元 1
醋 溜 土 豆 丝
12 元 1
(小)
豉汁排骨(小) 30 元 1
手撕包菜(小) 12 元 1
米饭 3 元 2
三. 解答题
17. 计算:( ) + |√2 3| ( √5) 4sin30°.
3 1 > 2( + 1)
18. 解不等式组: ,并在数轴上表示出其解集.
≤ 1
第 3页 /共 8页
19. 已知关于 x 的一元二次方程 ( 2) + 2 + + 3 = 0 有两个不相等实数根.
(1) 求 m 的取值范围;
(2) 当 m 取满足条件的最大整数时, 求方程的根.
20. 如图, 在□ABCD 中, = 2 . E, F 分别是 BC, AD 的中点, AE 和 BF 交于点 O,
连接 EF, OC.
(1)求证:四边形 ABEF 是菱形;
(2)若 = 8, ∠ = 60°, 求 OC 的长.
21. 北京世界园艺博览会(以下简称“世园会”)于 2019 年 4 月 29 日至 10 月 7 日在北京
市延庆区举行. 世园会为满足大家的游览需求, 倾情打造了 4 条各具特色的游玩路
线, 如下表:
A B C D
漫步世园会 爱家乡,爱园艺 清新园艺之旅 车览之旅
小美和小红都计划去世园会游玩,她们各自在这 4 条路线中任意选择一条,每条线
路被选择的可能性相同.
(1) 求小美选择路线“清新园艺之旅”的概率是多少?
(2) 用画树状图或列表的方法,求小美和小红恰好选择同一条路线的概率.
第 4页 /共 8页
22. 某商场销售一种进价为每件 10 元的日用商品, 经调查发现, 该商品每天的销售量
(件)与销售单价 (元)满足 = 10 + 400, 设销售这种商品每天的利润为 (元).
(1) 求 W 关于 x 的函数解析式;
(2) 在保证销售量尽可能大的前提下,若该商场每天想获得 2000 元的利润,应将销售
单价定为多少元
(3) 当每天销售量不少于 50 件,且销售单价至少为 32 元时,该商场每天获得的最大
利润是多少
23. 在平面直角坐标系 xOy 中,直线 = + ( < 0),经过点(6,0),且与坐标轴围
成的三角形的面积是 9,与函数 = ( > 0)的图象 G 交于 A,B 两点.
(1)求直线的表达式;
(2)横、纵坐标都是整数的点叫作整点.记图象 G 在点 A、B 之间的部分与线段 AB 围
成的区域(不含边界)为 W.
①当 = 2时,直接写出区域 W 内的整点的坐标______;
②若区域 W 内恰有 3 个整数点,结合函数图象,求 m 的取值范围.
第 5页 /共 8页
24. 如图, AB 是⊙O 的直径, 点 C 在⊙O 上, 点 P 是⊙O 上一动点, 且与点 C 分别位于
4
直径 AB 的两侧, tan∠CPB , 过点 C 作CQ⊥CP 交 PB 的延长线于点 Q;
3
(1) 当点 P 运动到什么位置时, CQ 恰好是⊙O 的切线?画出图形并加以说明。
(2) 若点 P 与点 C 关于直径 AB 对称, 且 AB=5, 画出图形求此时 CQ 的长.
C C
A B A B
O O
备用图
25. 如图, 在矩形 ABCD 中, E 是 BA 延长线上的定点,
M 为 BC 边上的一个动点, 连接 ME, 将射线 ME
绕点 M 顺时针旋转 76 , 交射线 CD 于点 F, 连接 MD.
小东根据学习函数的经验, 对线段 BM, DF, DM 的长度之间的关系进行了探究.
下面是小东探究的过程, 请补充完整:
(1) 对于点 M 在 BC 上的不同位置, 画图、测量, 得到了线段 BM, DF, DM 的长度的
几组值, 如下表:
位置 位置 位置 位置 位置 位置 位置 位置 位置
1 2 3 4 5 6 7 8 9
BM/cm 0.00 0.53 1.00 1.69 2.17 2.96 3.46 3.79. 4.00
DF/cm 0.00 1.00 1.74 2.49 2.69 2.21 1.14 0.00 1.00
DM/cm 4.12 3.61 3.16 2.52 2.09 1.44 1.14 1.02 1.00
第 6页 /共 8页
在 BM, DF, DM 的长度这三个量中, 确定
的长度是自变量, 的长度
和 的长度都是这个自变量的函数;
(2) 在同一平面直角坐标系 xOy 中, 画出 (1)
中所确定的两个函数的图象;
(3) 结合画出的函数图象, 解决问题: 当
DF=2cm 时, DM 的长度约为 cm.
26. 在平面直角坐标系 xOy 中, 有抛物线 = 3 4 + 3 和直线 y=3x+6.
其中, 直线与 x 轴, y 轴分别交于点 A, B. 将点 B 向右平移 6 个单位长度, 得到点 C.
(1) 求点 C 的坐标和抛物线的对称轴;
(2) 若抛物线与折线段 A-B-C 恰有两个公共点, 结合函数图象, 求 m 的取值范围.
27. 在△ 中, ∠ = 120°, = , = √3 , 设∠ = , ∠ = .
(1)如图 1, 当点 P 在△ 内,
① 若 = 153°, 求 的度数;
小明同学通过分析已知条件发现: △ 是顶角为120°的等腰三角形, 且 = √3 ,
从而容易联想到构造一个顶角为120°的等腰三角形. 于是, 他过点 A 作∠DAP=120°,
且 = , 连接 DP, DB, 发现两个不同的三角形全等: ≌ , 再利用全
等三角形及等腰三角形的相关知识可求出 的度数.
请利用小王同学分析的思路, 通过计算求得 的度数为______;
② 小王在①的基础上进一步进行探索, 发现 、 之间存在一种特殊的等量关系, 请写
出这个等量关系, 并加以证明.
第 7页 /共 8页
(2)如图 2, 点 P 在△ 外, 那么 、 之间的数量关系是否改变 若改变, 请直接写出
P
它们的数量关系; 若不变, 请说明理由.
A
D
AP
B C
B C
图 1 图 2
28. 对于平面直角坐标系 xOy 上的点 P 和⊙C, 定义如下: 若⊙C 上存在两个点 A, B,
使得点 P 在射线 BC 上, 且∠ = ∠ (0° < ∠ < 180°), 则称 P 为⊙C 的依附
点.
(1) 当⊙O 的半径为 1 时
① 已知点 ( 2.5,0), (0, 2), (1,0), 在点 D, E, F 中, ⊙O 的依附点是______;
② 点 T 在直线 = 上, 若 T 为⊙O 的依附点, 求点 T 的横坐标 t 的取值范围;
(2) ⊙C 的圆心在 x 轴上, 半径为 1,直线 = 2 + 2与 x 轴、y 轴分别交于点 M、N,
若线段 MN 上的所有点都是⊙C 的依附点, 请求出圆心 C 的横坐标 的取值范围.
第 8页 /共 8页
同课章节目录
