5.4平移 期中复习知识点分类练习题(含解析) 人教版七年级数学下册
文档属性
| 名称 | 5.4平移 期中复习知识点分类练习题(含解析) 人教版七年级数学下册 |

|
|
| 格式 | zip | ||
| 文件大小 | 243.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-17 09:25:11 | ||
图片预览

文档简介
人教版七年级数学下册《5.4平移》期中复习知识点分类练习题(附答案)
一.生活中的平移现象
1.下列生活中的物体的运动情况可以看成平移的是( )
A.钟摆的摆动 B.随风摆动的旗帜
C.在笔直的公路上行驶的汽车 D.在荡秋千的小朋友
2.小明乘电梯从一楼到六楼,向上平移了15米,若每层楼的高度相同,则她乘电梯从十三楼到一楼( )
A.向下平移28.8米 B.向下平移33米
C.向下平移26.4米 D.向下平移36米
3.如图所示:某公园里有一处长方形风景欣赏区ABCD,AB长50米,BC宽25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小明同学在假期沿着小路的中间行走(图中虚线),则:小明同学所走的路径长约为( )米.(小路的宽度忽略不计)
A.150米 B.125米 C.100米 D.75米
4.如图,在长为xm,宽为ym的长方形草地ABCD中有两条小路l1和l2.l1为W状,l2为平行四边形状,每条小路的右边线都是由小路左边线右移1m得到的两条小路l1、l2占地面积的情况是( )
A.l1占地面积大 B.l2占地面积大
C.l2和l1占地面积一样大 D.无法确定
5.如图,长方形ABCD的对角线AC=5,AB=3,BC=4,则图中五个小长方形的周长之和为( )
A.7 B.9 C.14 D.18
6.如图,在一块长20m,宽10m的长方形草地上,修建两条宽为1m的长方形小路,则这块草地的绿地面积(图中空白部分)为 m2.
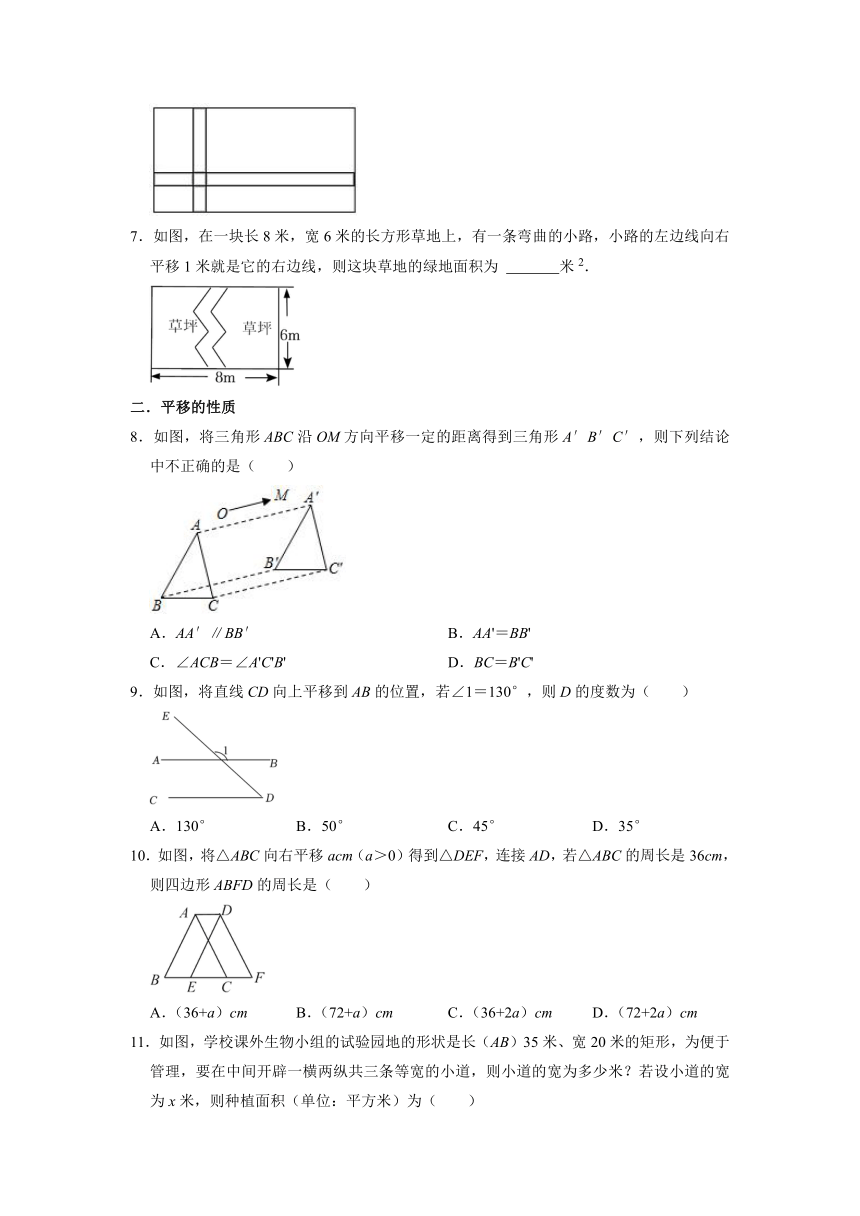
7.如图,在一块长8米,宽6米的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1米就是它的右边线,则这块草地的绿地面积为 米2.
二.平移的性质
8.如图,将三角形ABC沿OM方向平移一定的距离得到三角形A′B′C′,则下列结论中不正确的是( )
A.AA′∥BB′ B.AA'=BB'
C.∠ACB=∠A'C'B' D.BC=B'C'
9.如图,将直线CD向上平移到AB的位置,若∠1=130°,则D的度数为( )
A.130° B.50° C.45° D.35°
10.如图,将△ABC向右平移acm(a>0)得到△DEF,连接AD,若△ABC的周长是36cm,则四边形ABFD的周长是( )
A.(36+a)cm B.(72+a)cm C.(36+2a)cm D.(72+2a)cm
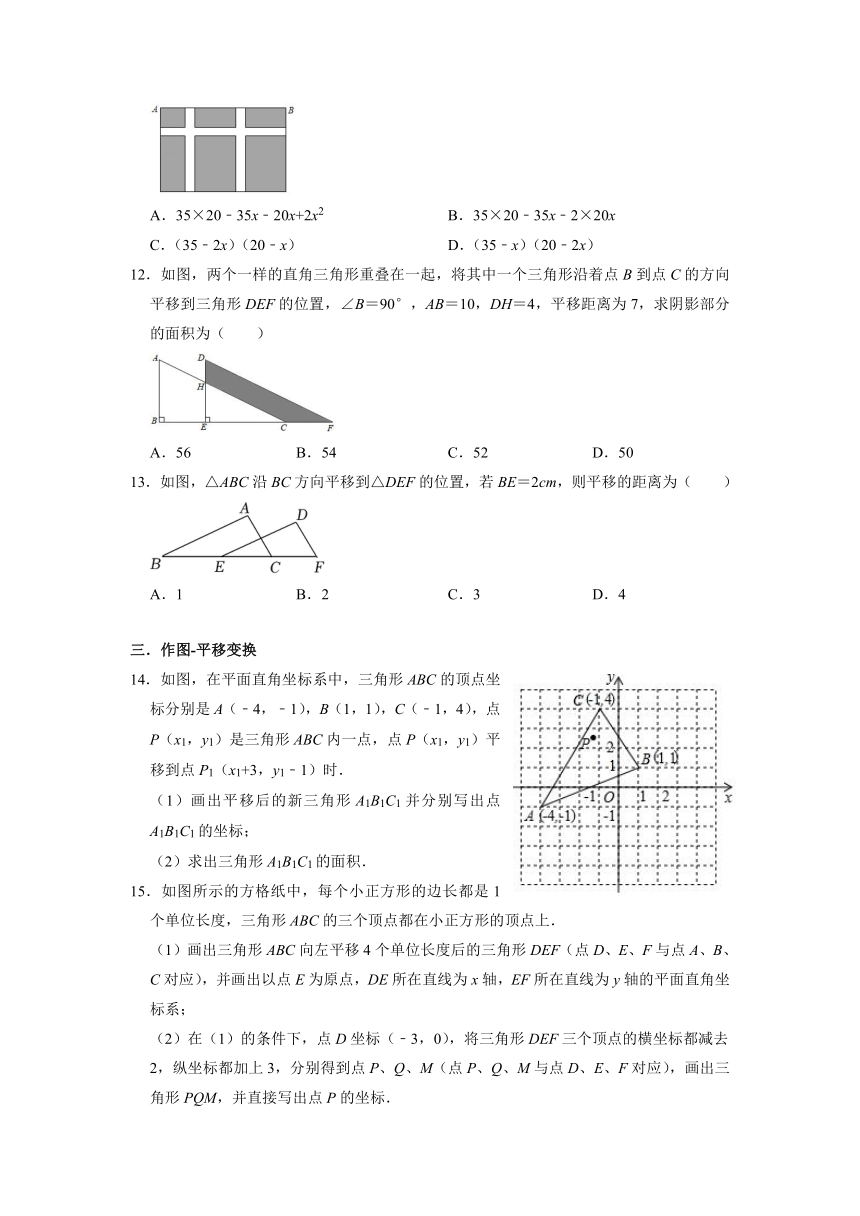
11.如图,学校课外生物小组的试验园地的形状是长(AB)35米、宽20米的矩形,为便于管理,要在中间开辟一横两纵共三条等宽的小道,则小道的宽为多少米?若设小道的宽为x米,则种植面积(单位:平方米)为( )
A.35×20﹣35x﹣20x+2x2 B.35×20﹣35x﹣2×20x
C.(35﹣2x)(20﹣x) D.(35﹣x)(20﹣2x)
12.如图,两个一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到三角形DEF的位置,∠B=90°,AB=10,DH=4,平移距离为7,求阴影部分的面积为( )
A.56 B.54 C.52 D.50
13.如图,△ABC沿BC方向平移到△DEF的位置,若BE=2cm,则平移的距离为( )
A.1 B.2 C.3 D.4
三.作图-平移变换
14.如图,在平面直角坐标系中,三角形ABC的顶点坐标分别是A(﹣4,﹣1),B(1,1),C(﹣1,4),点P(x1,y1)是三角形ABC内一点,点P(x1,y1)平移到点P1(x1+3,y1﹣1)时.
(1)画出平移后的新三角形A1B1C1并分别写出点A1B1C1的坐标;
(2)求出三角形A1B1C1的面积.
15.如图所示的方格纸中,每个小正方形的边长都是1个单位长度,三角形ABC的三个顶点都在小正方形的顶点上.
(1)画出三角形ABC向左平移4个单位长度后的三角形DEF(点D、E、F与点A、B、C对应),并画出以点E为原点,DE所在直线为x轴,EF所在直线为y轴的平面直角坐标系;
(2)在(1)的条件下,点D坐标(﹣3,0),将三角形DEF三个顶点的横坐标都减去2,纵坐标都加上3,分别得到点P、Q、M(点P、Q、M与点D、E、F对应),画出三角形PQM,并直接写出点P的坐标.
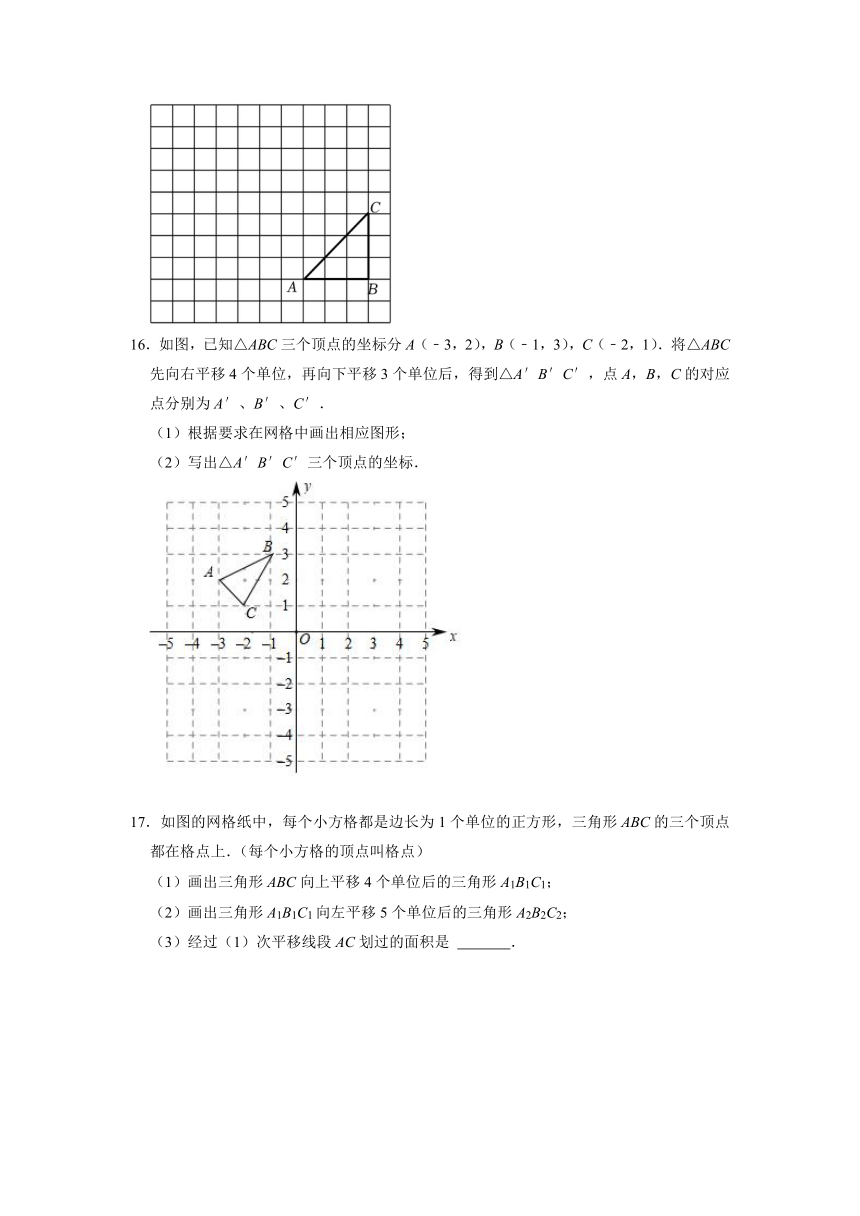
16.如图,已知△ABC三个顶点的坐标分A(﹣3,2),B(﹣1,3),C(﹣2,1).将△ABC先向右平移4个单位,再向下平移3个单位后,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′.
(1)根据要求在网格中画出相应图形;
(2)写出△A′B′C′三个顶点的坐标.
17.如图的网格纸中,每个小方格都是边长为1个单位的正方形,三角形ABC的三个顶点都在格点上.(每个小方格的顶点叫格点)
(1)画出三角形ABC向上平移4个单位后的三角形A1B1C1;
(2)画出三角形A1B1C1向左平移5个单位后的三角形A2B2C2;
(3)经过(1)次平移线段AC划过的面积是 .
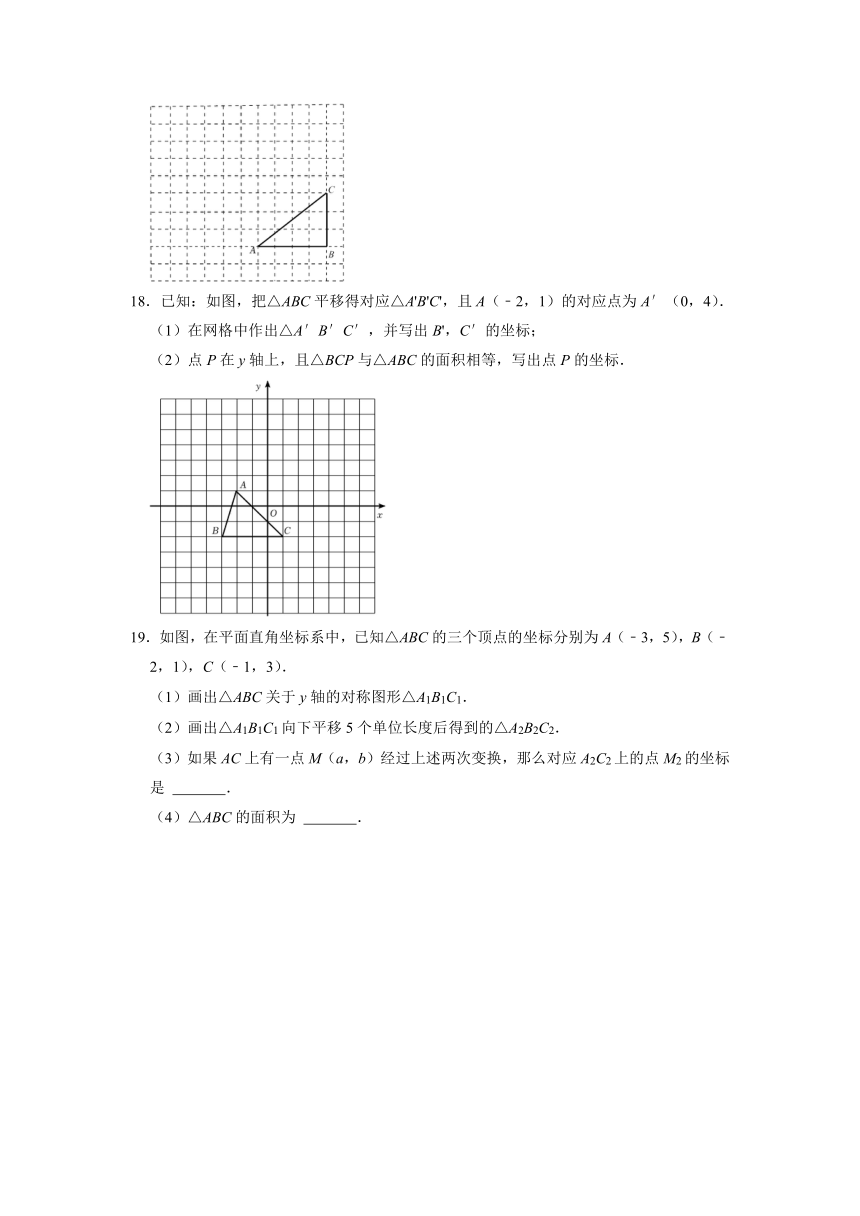
18.已知:如图,把△ABC平移得对应△A'B'C',且A(﹣2,1)的对应点为A′(0,4).
(1)在网格中作出△A′B′C′,并写出B',C′的坐标;
(2)点P在y轴上,且△BCP与△ABC的面积相等,写出点P的坐标.
19.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)画出△ABC关于y轴的对称图形△A1B1C1.
(2)画出△A1B1C1向下平移5个单位长度后得到的△A2B2C2.
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .
(4)△ABC的面积为 .
20.如图,点A,B,C,D,E,F,G均在单位正方形网格的格点(小正方形的顶点)上,建立平面直角坐标系,使得A,B的坐标分别为(﹣2,0)和(1,2).
(1)在图中画出该平面直角坐标系.
(2)指出点C,D,E,F,G所在的象限或坐标轴.
(3)平移四边形BEFG,使得点E与点C重合,得到四边形CF'G'B'(点F,G,B的对应点分别为点F',G',B'),画出四边形CF'G'B',并写出点C,F',G',B'的坐标.
参考答案
一.生活中的平移现象
1.解:A、改变了方向,不是平移,故此选项不符合题意;
B、改变了方向,不是平移,故此选项不符合题意;
C、符合平移的定义,是平移,故此选项符合题意;
D、改变了方向,不是平移,故此选项不符合题意.
故选:C.
2.解:∵从1楼到六楼,向上平移了15米.
∴每层楼高:15÷(6﹣1)=3(米)
∴从13楼到1楼需要向下平移:(13﹣1)×3=36(米).
故选:D.
3.解:由平移的性质可知,由于小路的宽度忽略不计,因此说行走的路程为AD+AB+BC=25+50+25=100(米),
故选:C.
4.解:小路l1的面积为:xy﹣(x﹣1)y=xy﹣xy+y=y;
小路l2的面积为:xy﹣(x﹣1)y=xy﹣xy+y=y.
所以l2和l1占地面积一样大.
故选:C.
5.解:图中五个小长方形的周长之和=AB+BC+CD+AD=3+4+3+4=14.
故选:C.
6.解:由题意得:
(20﹣1)×(10﹣1)
=19×9
=171(平方米),
答:这块草地的绿地面积(图中空白部分)为171平方米,
故答案为:171.
7.解:由题意得:
(8﹣1)×6
=7×6
=42(平方米),
所以:这块草地的绿地面积为42平方米,
故答案为:42.
二.平移的性质
8.解:∵三角形ABC沿OM方向平移一定的距离得到三角形A'B'C',
∴AA'∥BB',故A正确;
AA'=BB',故B正确;
∠ACB=∠A′C′B′,故C错误;
BC=B'C',故D正确,
故选:C.
9.解:∵∠1和∠2是邻补角,
∴∠1+∠2=180°,
∵∠1=130°,
∴∠2=180°﹣∠1=50°,
∵AB∥CD,
∴∠D=∠2=50°,
故选:B.
10.解:∵将周长为36cm的△ABC沿边BC向右平移a个单位得到△DEF,
∴AD=a,BF=BC+CF=BC+a,DF=AC,
又∵AB+BC+AC=36cm,
∴四边形ABFD的周长=AD+AB+BF+DF=a+AB+BC+a+AC=(36+2a)(cm).
故选:C.
11.解:依题意,得:(35﹣2x)(20﹣x),
故选:C.
12.解:∵平移距离为7,
∴BE=7,DE=AB,
∵AB=10,DH=4,
∴EH=10﹣4=6,
∵S△ABC=S△DEF,
∴S四边形ABEH=S阴,
∴阴影部分的面积为=×(10+6)×7=56,
故选:A.
13.解:△ABC沿BC方向平移到△DEF的位置,若BE=2cm,
则平移的距离为2cm,
故选:B.
三.作图-平移变换
14.解:(1)∵点P(x1,y1)平移到点P1(x1+3,y1﹣1),
∴平移的规律为:向右平移3个单位,向下平移1个单位,
∴A1为(﹣1,﹣2),B1为(4,0),C1为(2,3),
平移后的三角形如图所示:
(2)三角形A1B1C1面积为:5×5﹣×5×2﹣×5×3﹣×3×2=.
15.解:(1)△DEF如图所示;
(2)△PQM如图所示;P(﹣5,3).
16.解:(1)如图,△A′B′C′为所作;
(2)A′(1,﹣1),B′(3,0),C′(2,﹣2).
17.解:(1)如图,A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)经过(1)次平移线段AC划过的面积=4×4=16.
故答案为:16.
18.解:(1)如图,△A′B′C′为所作,B'(﹣1,1),C′(3,1);
(2)设P(0,t),
∵△BCP与△ABC的面积相等,
∴P点和A点到BC的距离相等,
而A点到BC的距离为3,
∴P点到BC的距离为3,
∴点P的坐标为(0,1)或(0,﹣5).
19.解:(1)如图所示,△A1B1C1即为所求;
(2)如上图所示,△A2B2C2即为所求;
(3)点M经过第一次变换后坐标为(﹣a,b),经过第二次变换后的坐标为(﹣a,b﹣5),
故答案为:(﹣a,b﹣5);
(4)S△ABC=4×2﹣=3,
故答案为:3.
20.解:(1)如图,
(2)C点、D点都在第二象限,点E、F、G都在第一象限;
(3)如图,四边形CF'G'B'为所作,C(﹣1,5),F'(1,7),G'(﹣1,9),B'(﹣3,7).
一.生活中的平移现象
1.下列生活中的物体的运动情况可以看成平移的是( )
A.钟摆的摆动 B.随风摆动的旗帜
C.在笔直的公路上行驶的汽车 D.在荡秋千的小朋友
2.小明乘电梯从一楼到六楼,向上平移了15米,若每层楼的高度相同,则她乘电梯从十三楼到一楼( )
A.向下平移28.8米 B.向下平移33米
C.向下平移26.4米 D.向下平移36米
3.如图所示:某公园里有一处长方形风景欣赏区ABCD,AB长50米,BC宽25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小明同学在假期沿着小路的中间行走(图中虚线),则:小明同学所走的路径长约为( )米.(小路的宽度忽略不计)
A.150米 B.125米 C.100米 D.75米
4.如图,在长为xm,宽为ym的长方形草地ABCD中有两条小路l1和l2.l1为W状,l2为平行四边形状,每条小路的右边线都是由小路左边线右移1m得到的两条小路l1、l2占地面积的情况是( )
A.l1占地面积大 B.l2占地面积大
C.l2和l1占地面积一样大 D.无法确定
5.如图,长方形ABCD的对角线AC=5,AB=3,BC=4,则图中五个小长方形的周长之和为( )
A.7 B.9 C.14 D.18
6.如图,在一块长20m,宽10m的长方形草地上,修建两条宽为1m的长方形小路,则这块草地的绿地面积(图中空白部分)为 m2.
7.如图,在一块长8米,宽6米的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1米就是它的右边线,则这块草地的绿地面积为 米2.
二.平移的性质
8.如图,将三角形ABC沿OM方向平移一定的距离得到三角形A′B′C′,则下列结论中不正确的是( )
A.AA′∥BB′ B.AA'=BB'
C.∠ACB=∠A'C'B' D.BC=B'C'
9.如图,将直线CD向上平移到AB的位置,若∠1=130°,则D的度数为( )
A.130° B.50° C.45° D.35°
10.如图,将△ABC向右平移acm(a>0)得到△DEF,连接AD,若△ABC的周长是36cm,则四边形ABFD的周长是( )
A.(36+a)cm B.(72+a)cm C.(36+2a)cm D.(72+2a)cm
11.如图,学校课外生物小组的试验园地的形状是长(AB)35米、宽20米的矩形,为便于管理,要在中间开辟一横两纵共三条等宽的小道,则小道的宽为多少米?若设小道的宽为x米,则种植面积(单位:平方米)为( )
A.35×20﹣35x﹣20x+2x2 B.35×20﹣35x﹣2×20x
C.(35﹣2x)(20﹣x) D.(35﹣x)(20﹣2x)
12.如图,两个一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到三角形DEF的位置,∠B=90°,AB=10,DH=4,平移距离为7,求阴影部分的面积为( )
A.56 B.54 C.52 D.50
13.如图,△ABC沿BC方向平移到△DEF的位置,若BE=2cm,则平移的距离为( )
A.1 B.2 C.3 D.4
三.作图-平移变换
14.如图,在平面直角坐标系中,三角形ABC的顶点坐标分别是A(﹣4,﹣1),B(1,1),C(﹣1,4),点P(x1,y1)是三角形ABC内一点,点P(x1,y1)平移到点P1(x1+3,y1﹣1)时.
(1)画出平移后的新三角形A1B1C1并分别写出点A1B1C1的坐标;
(2)求出三角形A1B1C1的面积.
15.如图所示的方格纸中,每个小正方形的边长都是1个单位长度,三角形ABC的三个顶点都在小正方形的顶点上.
(1)画出三角形ABC向左平移4个单位长度后的三角形DEF(点D、E、F与点A、B、C对应),并画出以点E为原点,DE所在直线为x轴,EF所在直线为y轴的平面直角坐标系;
(2)在(1)的条件下,点D坐标(﹣3,0),将三角形DEF三个顶点的横坐标都减去2,纵坐标都加上3,分别得到点P、Q、M(点P、Q、M与点D、E、F对应),画出三角形PQM,并直接写出点P的坐标.
16.如图,已知△ABC三个顶点的坐标分A(﹣3,2),B(﹣1,3),C(﹣2,1).将△ABC先向右平移4个单位,再向下平移3个单位后,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′.
(1)根据要求在网格中画出相应图形;
(2)写出△A′B′C′三个顶点的坐标.
17.如图的网格纸中,每个小方格都是边长为1个单位的正方形,三角形ABC的三个顶点都在格点上.(每个小方格的顶点叫格点)
(1)画出三角形ABC向上平移4个单位后的三角形A1B1C1;
(2)画出三角形A1B1C1向左平移5个单位后的三角形A2B2C2;
(3)经过(1)次平移线段AC划过的面积是 .
18.已知:如图,把△ABC平移得对应△A'B'C',且A(﹣2,1)的对应点为A′(0,4).
(1)在网格中作出△A′B′C′,并写出B',C′的坐标;
(2)点P在y轴上,且△BCP与△ABC的面积相等,写出点P的坐标.
19.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)画出△ABC关于y轴的对称图形△A1B1C1.
(2)画出△A1B1C1向下平移5个单位长度后得到的△A2B2C2.
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .
(4)△ABC的面积为 .
20.如图,点A,B,C,D,E,F,G均在单位正方形网格的格点(小正方形的顶点)上,建立平面直角坐标系,使得A,B的坐标分别为(﹣2,0)和(1,2).
(1)在图中画出该平面直角坐标系.
(2)指出点C,D,E,F,G所在的象限或坐标轴.
(3)平移四边形BEFG,使得点E与点C重合,得到四边形CF'G'B'(点F,G,B的对应点分别为点F',G',B'),画出四边形CF'G'B',并写出点C,F',G',B'的坐标.
参考答案
一.生活中的平移现象
1.解:A、改变了方向,不是平移,故此选项不符合题意;
B、改变了方向,不是平移,故此选项不符合题意;
C、符合平移的定义,是平移,故此选项符合题意;
D、改变了方向,不是平移,故此选项不符合题意.
故选:C.
2.解:∵从1楼到六楼,向上平移了15米.
∴每层楼高:15÷(6﹣1)=3(米)
∴从13楼到1楼需要向下平移:(13﹣1)×3=36(米).
故选:D.
3.解:由平移的性质可知,由于小路的宽度忽略不计,因此说行走的路程为AD+AB+BC=25+50+25=100(米),
故选:C.
4.解:小路l1的面积为:xy﹣(x﹣1)y=xy﹣xy+y=y;
小路l2的面积为:xy﹣(x﹣1)y=xy﹣xy+y=y.
所以l2和l1占地面积一样大.
故选:C.
5.解:图中五个小长方形的周长之和=AB+BC+CD+AD=3+4+3+4=14.
故选:C.
6.解:由题意得:
(20﹣1)×(10﹣1)
=19×9
=171(平方米),
答:这块草地的绿地面积(图中空白部分)为171平方米,
故答案为:171.
7.解:由题意得:
(8﹣1)×6
=7×6
=42(平方米),
所以:这块草地的绿地面积为42平方米,
故答案为:42.
二.平移的性质
8.解:∵三角形ABC沿OM方向平移一定的距离得到三角形A'B'C',
∴AA'∥BB',故A正确;
AA'=BB',故B正确;
∠ACB=∠A′C′B′,故C错误;
BC=B'C',故D正确,
故选:C.
9.解:∵∠1和∠2是邻补角,
∴∠1+∠2=180°,
∵∠1=130°,
∴∠2=180°﹣∠1=50°,
∵AB∥CD,
∴∠D=∠2=50°,
故选:B.
10.解:∵将周长为36cm的△ABC沿边BC向右平移a个单位得到△DEF,
∴AD=a,BF=BC+CF=BC+a,DF=AC,
又∵AB+BC+AC=36cm,
∴四边形ABFD的周长=AD+AB+BF+DF=a+AB+BC+a+AC=(36+2a)(cm).
故选:C.
11.解:依题意,得:(35﹣2x)(20﹣x),
故选:C.
12.解:∵平移距离为7,
∴BE=7,DE=AB,
∵AB=10,DH=4,
∴EH=10﹣4=6,
∵S△ABC=S△DEF,
∴S四边形ABEH=S阴,
∴阴影部分的面积为=×(10+6)×7=56,
故选:A.
13.解:△ABC沿BC方向平移到△DEF的位置,若BE=2cm,
则平移的距离为2cm,
故选:B.
三.作图-平移变换
14.解:(1)∵点P(x1,y1)平移到点P1(x1+3,y1﹣1),
∴平移的规律为:向右平移3个单位,向下平移1个单位,
∴A1为(﹣1,﹣2),B1为(4,0),C1为(2,3),
平移后的三角形如图所示:
(2)三角形A1B1C1面积为:5×5﹣×5×2﹣×5×3﹣×3×2=.
15.解:(1)△DEF如图所示;
(2)△PQM如图所示;P(﹣5,3).
16.解:(1)如图,△A′B′C′为所作;
(2)A′(1,﹣1),B′(3,0),C′(2,﹣2).
17.解:(1)如图,A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)经过(1)次平移线段AC划过的面积=4×4=16.
故答案为:16.
18.解:(1)如图,△A′B′C′为所作,B'(﹣1,1),C′(3,1);
(2)设P(0,t),
∵△BCP与△ABC的面积相等,
∴P点和A点到BC的距离相等,
而A点到BC的距离为3,
∴P点到BC的距离为3,
∴点P的坐标为(0,1)或(0,﹣5).
19.解:(1)如图所示,△A1B1C1即为所求;
(2)如上图所示,△A2B2C2即为所求;
(3)点M经过第一次变换后坐标为(﹣a,b),经过第二次变换后的坐标为(﹣a,b﹣5),
故答案为:(﹣a,b﹣5);
(4)S△ABC=4×2﹣=3,
故答案为:3.
20.解:(1)如图,
(2)C点、D点都在第二象限,点E、F、G都在第一象限;
(3)如图,四边形CF'G'B'为所作,C(﹣1,5),F'(1,7),G'(﹣1,9),B'(﹣3,7).
