2022-2023学年北师大版七年级数学下册4.5 利用三角形全等测距离 练习题(无答案)
文档属性
| 名称 | 2022-2023学年北师大版七年级数学下册4.5 利用三角形全等测距离 练习题(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 396.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-17 00:00:00 | ||
图片预览


文档简介
4.5 利用三角形全等测距离(练习题)-北师大版七年级下册
一.选择题
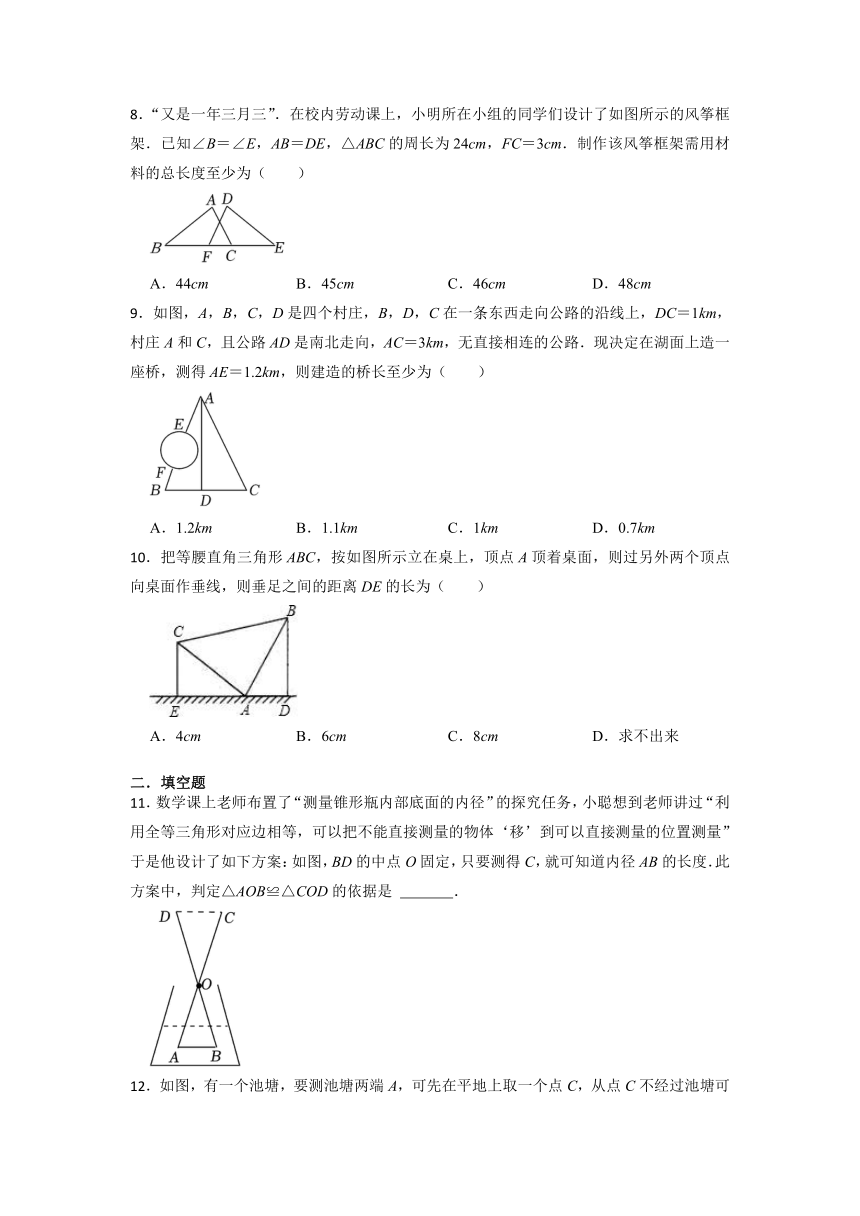
.如图,小亮要测量水池AB的宽度,但没有足够长的绳子,请将方案补充完整,并说明方案成立的理由,( )
(1)先在地上取一个可以直接到达A点和B点的点C;
(2)连接BC并延长到E,使得△;
(3)连接AC并延长到D,使得▽;
(4)连接O并测量出它的长度,就是AB的长;
(5)上述方案的依据是◇.
A.△代表CE=BC B.▽代表CD=CA C.〇代表DE D.◇代表SSS
.李老师一块教学用的三角形玻璃不小心打破了,他想再到玻璃店划一块同样大小的三角形玻璃,为了方便他只要带哪一块就可以( )
A.③ B.② C.① D.都不行
.如图,小健家的仿古家具有一块三角形形状的玻璃坏了,需要重新配一块.将该三角形记为△ABC,则提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( )
A.AB,BC,CA B.∠B,BC,CA C.∠A,AB,CA D.∠A,∠B,CA
.如图,小亮要测量水池AB的宽度,但没有足够长的绳子,并说明方案成立的理由.
(1)先在地上取一个可以直接到达A点和B点的点C;
(2)连接BC并延长到E,使得△,
(3)连接AC并延长到D,使得▽;
(4)连接〇并测量出它的长度,就是AB的长.
(5)上述方案的依据是◇.
错误的选项是( )
A.△代表CE=BC B.▽代表CD=CA C.〇代表DE D.◇代表SSS
.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等( )
A.60° B.75° C.90° D.120°
.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,测得AB=5厘米,EF=6厘米( )
A.5厘米 B.6厘米 C.1厘米 D.厘米
.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角中∠ABC=32°( )
A.32° B.62° C.58° D.68°
.“又是一年三月三”.在校内劳动课上,小明所在小组的同学们设计了如图所示的风筝框架.已知∠B=∠E,AB=DE,△ABC的周长为24cm,FC=3cm.制作该风筝框架需用材料的总长度至少为( )
A.44cm B.45cm C.46cm D.48cm
.如图,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,DC=1km,村庄A和C,且公路AD是南北走向,AC=3km,无直接相连的公路.现决定在湖面上造一座桥,测得AE=1.2km,则建造的桥长至少为( )
A.1.2km B.1.1km C.1km D.0.7km
.把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
A.4cm B.6cm C.8cm D.求不出来
二.填空题
.数学课上老师布置了“测量锥形瓶内部底面的内径”的探究任务,小聪想到老师讲过“利用全等三角形对应边相等,可以把不能直接测量的物体‘移’到可以直接测量的位置测量”于是他设计了如下方案:如图,BD的中点O固定,只要测得C,就可知道内径AB的长度.此方案中,判定△AOB≌△COD的依据是 .
.如图,有一个池塘,要测池塘两端A,可先在平地上取一个点C,从点C不经过池塘可以直接达到点A和B,使CD=CA,连接BC并延长到点E,连接DE,量出DE=8 .
.如图,要测量池塘两岸相对的两点A,B的距离,D,使BC=CD,再画出BF的垂线DE,C在一条直线上.若想知道两点A,B的距离 的长度即可,其中△ABC≌△EDC的理论依据是 .
.小明利用一根长3m的竿子CD来测量路灯杆AB的高度,方法如下:如图,在地面上选一点P,并测得∠APB=70°,然后把CD在BP的延长线上左右移动,此时测得BD=11.2m.
(1)此时∠C的度数为 ;
(2)路灯杆AB的高度为 m.
.嘉淇为了测量建筑物墙壁AB的高度,采用了如图所示的方法:
①把一根足够长的竹竿AC的顶端对齐建筑物顶端A,末端落在地面C处;
②把竹竿顶端沿AB下滑至点D,使DB= ,此时竹竿末端落在地面E处;
③测得EB的长度,就是AB的高度.
以上测量方法直接利用了全等三角形的判定方法 (用字母表示).
三.解答题
.明明同学用10块高度都是3cm的相同长方体小木块垒了两堵与地面垂直的木墙,木墙上面刚好可以放进一个等腰直角三角形(AC=BC,∠ACB=90°)点C在DE上,求两堵木墙之间的距离.
.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,你能帮他想个办法吗?
(1)把你的方法写出来.
(2)写出其中的道理.
.小明与爸爸妈妈在操场上荡秋千.小明坐在秋千上的起始位置A处,起始位置OA与地面垂直,两脚在地面上用力一蹬,妈妈用力一推,爸爸在C处接住他.若妈妈与爸爸到秋千起始位置OA的水平距离BF,∠BOC=90°.
(1)△CGO与△OFB全等吗?请说明理由;
(2)请直接写出爸爸在距离地面多高的地方接住小明.
.如图,某段河流的两岸是平行的,八(1)班数学兴趣小组在张老师带领下不用涉水过河就测得河的宽度
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走25m有一树C,继续前行25m到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处时停止行走;
④测得DE的长为20米.
根据他们的做法,回答下列问题:
(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
.如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若EF=10m,BF=3m,求FC的长度.
一.选择题
.如图,小亮要测量水池AB的宽度,但没有足够长的绳子,请将方案补充完整,并说明方案成立的理由,( )
(1)先在地上取一个可以直接到达A点和B点的点C;
(2)连接BC并延长到E,使得△;
(3)连接AC并延长到D,使得▽;
(4)连接O并测量出它的长度,就是AB的长;
(5)上述方案的依据是◇.
A.△代表CE=BC B.▽代表CD=CA C.〇代表DE D.◇代表SSS
.李老师一块教学用的三角形玻璃不小心打破了,他想再到玻璃店划一块同样大小的三角形玻璃,为了方便他只要带哪一块就可以( )
A.③ B.② C.① D.都不行
.如图,小健家的仿古家具有一块三角形形状的玻璃坏了,需要重新配一块.将该三角形记为△ABC,则提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( )
A.AB,BC,CA B.∠B,BC,CA C.∠A,AB,CA D.∠A,∠B,CA
.如图,小亮要测量水池AB的宽度,但没有足够长的绳子,并说明方案成立的理由.
(1)先在地上取一个可以直接到达A点和B点的点C;
(2)连接BC并延长到E,使得△,
(3)连接AC并延长到D,使得▽;
(4)连接〇并测量出它的长度,就是AB的长.
(5)上述方案的依据是◇.
错误的选项是( )
A.△代表CE=BC B.▽代表CD=CA C.〇代表DE D.◇代表SSS
.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等( )
A.60° B.75° C.90° D.120°
.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,测得AB=5厘米,EF=6厘米( )
A.5厘米 B.6厘米 C.1厘米 D.厘米
.如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角中∠ABC=32°( )
A.32° B.62° C.58° D.68°
.“又是一年三月三”.在校内劳动课上,小明所在小组的同学们设计了如图所示的风筝框架.已知∠B=∠E,AB=DE,△ABC的周长为24cm,FC=3cm.制作该风筝框架需用材料的总长度至少为( )
A.44cm B.45cm C.46cm D.48cm
.如图,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,DC=1km,村庄A和C,且公路AD是南北走向,AC=3km,无直接相连的公路.现决定在湖面上造一座桥,测得AE=1.2km,则建造的桥长至少为( )
A.1.2km B.1.1km C.1km D.0.7km
.把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
A.4cm B.6cm C.8cm D.求不出来
二.填空题
.数学课上老师布置了“测量锥形瓶内部底面的内径”的探究任务,小聪想到老师讲过“利用全等三角形对应边相等,可以把不能直接测量的物体‘移’到可以直接测量的位置测量”于是他设计了如下方案:如图,BD的中点O固定,只要测得C,就可知道内径AB的长度.此方案中,判定△AOB≌△COD的依据是 .
.如图,有一个池塘,要测池塘两端A,可先在平地上取一个点C,从点C不经过池塘可以直接达到点A和B,使CD=CA,连接BC并延长到点E,连接DE,量出DE=8 .
.如图,要测量池塘两岸相对的两点A,B的距离,D,使BC=CD,再画出BF的垂线DE,C在一条直线上.若想知道两点A,B的距离 的长度即可,其中△ABC≌△EDC的理论依据是 .
.小明利用一根长3m的竿子CD来测量路灯杆AB的高度,方法如下:如图,在地面上选一点P,并测得∠APB=70°,然后把CD在BP的延长线上左右移动,此时测得BD=11.2m.
(1)此时∠C的度数为 ;
(2)路灯杆AB的高度为 m.
.嘉淇为了测量建筑物墙壁AB的高度,采用了如图所示的方法:
①把一根足够长的竹竿AC的顶端对齐建筑物顶端A,末端落在地面C处;
②把竹竿顶端沿AB下滑至点D,使DB= ,此时竹竿末端落在地面E处;
③测得EB的长度,就是AB的高度.
以上测量方法直接利用了全等三角形的判定方法 (用字母表示).
三.解答题
.明明同学用10块高度都是3cm的相同长方体小木块垒了两堵与地面垂直的木墙,木墙上面刚好可以放进一个等腰直角三角形(AC=BC,∠ACB=90°)点C在DE上,求两堵木墙之间的距离.
.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,你能帮他想个办法吗?
(1)把你的方法写出来.
(2)写出其中的道理.
.小明与爸爸妈妈在操场上荡秋千.小明坐在秋千上的起始位置A处,起始位置OA与地面垂直,两脚在地面上用力一蹬,妈妈用力一推,爸爸在C处接住他.若妈妈与爸爸到秋千起始位置OA的水平距离BF,∠BOC=90°.
(1)△CGO与△OFB全等吗?请说明理由;
(2)请直接写出爸爸在距离地面多高的地方接住小明.
.如图,某段河流的两岸是平行的,八(1)班数学兴趣小组在张老师带领下不用涉水过河就测得河的宽度
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走25m有一树C,继续前行25m到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处时停止行走;
④测得DE的长为20米.
根据他们的做法,回答下列问题:
(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
.如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若EF=10m,BF=3m,求FC的长度.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
