苏科版七年级数学下册 9.3 多项式乘多项式 同步练习(含解析)
文档属性
| 名称 | 苏科版七年级数学下册 9.3 多项式乘多项式 同步练习(含解析) | 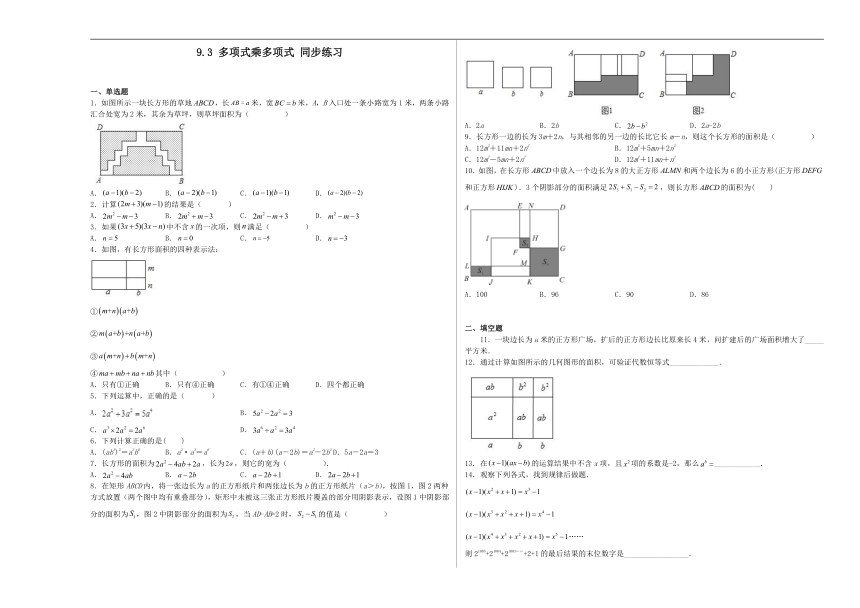 | |
| 格式 | zip | ||
| 文件大小 | 279.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-18 07:50:55 | ||
图片预览



文档简介
9.3 多项式乘多项式 同步练习
一、单选题
1.如图所示一块长方形的草地,长米,宽米,A,B入口处一条小路宽为1米,两条小路汇合处宽为2米,其余为草坪,则草坪面积为( )
A. B. C. D.
2.计算的结果是( )
A. B. C. D.
3.如果中不含的一次项,则满足( )
A. B. C. D.
4.如图,有长方形面积的四种表示法:
①
②
③
④其中( )
A.只有①正确 B.只有④正确 C.有①④正确 D.四个都正确
5.下列运算中,正确的是( )
A. B.
C. D.
6.下列计算正确的是( )
A.(ab3)2=a2b6 B.a2·a3=a6 C.(a+b)(a-2b)=a2-2b2 D.5a-2a=3
7.长方形的面积为,长为,则它的宽为( ).
A. B. C. D.
8.在矩形ABCD内,将一张边长为a的正方形纸片和两张边长为b的正方形纸片(a>b),按图1,图2两种方式放置(两个图中均有重叠部分),矩形中未被这三张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为,图2中阴影部分的面积为,当AD-AB=2时,的值是( )
A.2a B.2b C. D.2a-2b
9.长方形一边的长为3m+2n,与其相邻的另一边的长比它长m-n,则这个长方形的面积是( )
A.12m2+11mn+2n2 B.12m2+5mn+2n2
C.12m2-5mn+2n2 D.12m2+11mn+n2
10.如图,在长方形中放入一个边长为8的大正方形和两个边长为6的小正方形(正方形和正方形).3个阴影部分的面积满足,则长方形的面积为( )
A.100 B.96 C.90 D.86
二、填空题
11.一块边长为a米的正方形广场,扩后的正方形边长比原来长4米,问扩建后的广场面积增大了_____平方米.
12.通过计算如图所示的几何图形的面积,可验证代数恒等式_____________.
13.在的运算结果中不含x项,且项的系数是-2,那么____________.
14.观察下列各式,找到规律后做题.
……
则21005+21004+21003……+2+1的最后结果的末位数字是_________________.
15.若(x+2y)(2x﹣ky﹣1)的结果中不含xy项,则k的值为_____.
三、解答题
16.化简求值:(2x+y)2﹣(2x﹣y)(x+y)﹣2(x﹣2y)(x+2y),其中 x=,y=﹣2.
17.
18.化简求值:,其中.
参考答案
1.B
【详解】解:通过平移可将图中纵向的小路移到中间,将横向的小路平移到底边,如图所示:
∵AB=a米,宽BC=b米,
∴草坪面积为:(a-2)(b-1)(平方米).
故选:B.
2.B
【详解】.
故选B.
3.A
【详解】解:
∵中不含的一次项
∴
∴.
故选:A.
4.D
【详解】解:根据大长方形可求的面积为(m+n)(a+b),故①正确;
根据乘法分配律可知(m+n)(a+b)=m(a+b)+n(a+b)或(m+n)(a+b)=a(m+n)+b(m+n),故②③正确;
根据分解后的图形,可得面积为:an+bn+am+bm,故④正确.
故选:D
5.D
【详解】试题分析:根据合并同类项,同底幂乘法,同底幂乘除法运算法则逐一计算作出判断:
A.,选项错误;
B.,选项错误;
C.,选项错误;
D.,选项正确.
故选D.
6.A
详解:A.(ab3)2=a2b6,故本选项正确;
B.a2 a3=a5,故本选项错误;
C.(a+b)(a﹣2b)=a2﹣ab﹣2b2,故本选项错误;
D.5a﹣2a=3a,故本选项错误.
故选A.
7.C
【详解】解:由题意得:
(2a2-4ab+2a)÷(2a)=a-2b+1,
∴长方形的面积为2a2-4ab+2a,长为2a,则它的宽为:a-2b+1,
故选:C.
8.C
【详解】解:由图可得,
由图1得:,
由图2得:,
=
=
=
=,
∵ADAB=2,
∴原式=,
即=,
故选:C.
9.A
【详解】由题意得,长方形的另一边长为:3m+2n+m-n=4m+n,
所以长方形的面积为:
(3m+2n)(4m+n)
=12m2+3mn+8mn+2n2
=12m2+11mn+2n2,
故选A.
10.C
【详解】解:设长方形的长为,宽为,则由已知及图形可得:
的长为:,宽为:,故
的长为:,宽为:,故;
的长为:,宽为:,故.
∵,
整理得
故选:.
11.(8a+16).
【详解】解:由题意可得:(a+4)2﹣a2=(8a+16)平方米.
故答案为:(8a+16).
12.
【详解】解:如图,,,
则,即大长方形的另一条边的长为,
因此有,
即,
故答案为:.
13.4
【详解】解:
∵运算结果中不含x项,且项的系数是-2,
∴-(a+b)=0,a=-2
解得a=-2,b=2
∴,
故答案为:4.
14.3
【详解】解:
=
=,
∵,
∴2的指数幂的末位数字是以2、4、8、6为循环的,
∵1006÷4=251…2,
∴的末尾数字是4,的末尾数字是3,
故答案为:3.
15.4
【详解】解:(x+2y)(2x﹣ky﹣1)
=2x2﹣kxy﹣x+4xy﹣2ky2﹣2y
=2x2+(﹣k+4)xy﹣2ky2﹣2y﹣x,
∵(x+2y)(2x﹣ky﹣1)的结果中不含xy项,
∴﹣k+4=0,
解得:k=4,
故答案为4.
16.3xy+10y2;37.
【详解】解:原式=4x2+4xy+y2﹣(2x2+xy﹣y2)﹣2(x2﹣4y2)
=3xy+10y2;
将其中 ,y=﹣2代入,原式=3×(﹣2)× +10×(﹣2)2=37.
17.
【详解】解:原式
18.;
【详解】解:原式
.
当时,原式.
一、单选题
1.如图所示一块长方形的草地,长米,宽米,A,B入口处一条小路宽为1米,两条小路汇合处宽为2米,其余为草坪,则草坪面积为( )
A. B. C. D.
2.计算的结果是( )
A. B. C. D.
3.如果中不含的一次项,则满足( )
A. B. C. D.
4.如图,有长方形面积的四种表示法:
①
②
③
④其中( )
A.只有①正确 B.只有④正确 C.有①④正确 D.四个都正确
5.下列运算中,正确的是( )
A. B.
C. D.
6.下列计算正确的是( )
A.(ab3)2=a2b6 B.a2·a3=a6 C.(a+b)(a-2b)=a2-2b2 D.5a-2a=3
7.长方形的面积为,长为,则它的宽为( ).
A. B. C. D.
8.在矩形ABCD内,将一张边长为a的正方形纸片和两张边长为b的正方形纸片(a>b),按图1,图2两种方式放置(两个图中均有重叠部分),矩形中未被这三张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为,图2中阴影部分的面积为,当AD-AB=2时,的值是( )
A.2a B.2b C. D.2a-2b
9.长方形一边的长为3m+2n,与其相邻的另一边的长比它长m-n,则这个长方形的面积是( )
A.12m2+11mn+2n2 B.12m2+5mn+2n2
C.12m2-5mn+2n2 D.12m2+11mn+n2
10.如图,在长方形中放入一个边长为8的大正方形和两个边长为6的小正方形(正方形和正方形).3个阴影部分的面积满足,则长方形的面积为( )
A.100 B.96 C.90 D.86
二、填空题
11.一块边长为a米的正方形广场,扩后的正方形边长比原来长4米,问扩建后的广场面积增大了_____平方米.
12.通过计算如图所示的几何图形的面积,可验证代数恒等式_____________.
13.在的运算结果中不含x项,且项的系数是-2,那么____________.
14.观察下列各式,找到规律后做题.
……
则21005+21004+21003……+2+1的最后结果的末位数字是_________________.
15.若(x+2y)(2x﹣ky﹣1)的结果中不含xy项,则k的值为_____.
三、解答题
16.化简求值:(2x+y)2﹣(2x﹣y)(x+y)﹣2(x﹣2y)(x+2y),其中 x=,y=﹣2.
17.
18.化简求值:,其中.
参考答案
1.B
【详解】解:通过平移可将图中纵向的小路移到中间,将横向的小路平移到底边,如图所示:
∵AB=a米,宽BC=b米,
∴草坪面积为:(a-2)(b-1)(平方米).
故选:B.
2.B
【详解】.
故选B.
3.A
【详解】解:
∵中不含的一次项
∴
∴.
故选:A.
4.D
【详解】解:根据大长方形可求的面积为(m+n)(a+b),故①正确;
根据乘法分配律可知(m+n)(a+b)=m(a+b)+n(a+b)或(m+n)(a+b)=a(m+n)+b(m+n),故②③正确;
根据分解后的图形,可得面积为:an+bn+am+bm,故④正确.
故选:D
5.D
【详解】试题分析:根据合并同类项,同底幂乘法,同底幂乘除法运算法则逐一计算作出判断:
A.,选项错误;
B.,选项错误;
C.,选项错误;
D.,选项正确.
故选D.
6.A
详解:A.(ab3)2=a2b6,故本选项正确;
B.a2 a3=a5,故本选项错误;
C.(a+b)(a﹣2b)=a2﹣ab﹣2b2,故本选项错误;
D.5a﹣2a=3a,故本选项错误.
故选A.
7.C
【详解】解:由题意得:
(2a2-4ab+2a)÷(2a)=a-2b+1,
∴长方形的面积为2a2-4ab+2a,长为2a,则它的宽为:a-2b+1,
故选:C.
8.C
【详解】解:由图可得,
由图1得:,
由图2得:,
=
=
=
=,
∵ADAB=2,
∴原式=,
即=,
故选:C.
9.A
【详解】由题意得,长方形的另一边长为:3m+2n+m-n=4m+n,
所以长方形的面积为:
(3m+2n)(4m+n)
=12m2+3mn+8mn+2n2
=12m2+11mn+2n2,
故选A.
10.C
【详解】解:设长方形的长为,宽为,则由已知及图形可得:
的长为:,宽为:,故
的长为:,宽为:,故;
的长为:,宽为:,故.
∵,
整理得
故选:.
11.(8a+16).
【详解】解:由题意可得:(a+4)2﹣a2=(8a+16)平方米.
故答案为:(8a+16).
12.
【详解】解:如图,,,
则,即大长方形的另一条边的长为,
因此有,
即,
故答案为:.
13.4
【详解】解:
∵运算结果中不含x项,且项的系数是-2,
∴-(a+b)=0,a=-2
解得a=-2,b=2
∴,
故答案为:4.
14.3
【详解】解:
=
=,
∵,
∴2的指数幂的末位数字是以2、4、8、6为循环的,
∵1006÷4=251…2,
∴的末尾数字是4,的末尾数字是3,
故答案为:3.
15.4
【详解】解:(x+2y)(2x﹣ky﹣1)
=2x2﹣kxy﹣x+4xy﹣2ky2﹣2y
=2x2+(﹣k+4)xy﹣2ky2﹣2y﹣x,
∵(x+2y)(2x﹣ky﹣1)的结果中不含xy项,
∴﹣k+4=0,
解得:k=4,
故答案为4.
16.3xy+10y2;37.
【详解】解:原式=4x2+4xy+y2﹣(2x2+xy﹣y2)﹣2(x2﹣4y2)
=3xy+10y2;
将其中 ,y=﹣2代入,原式=3×(﹣2)× +10×(﹣2)2=37.
17.
【详解】解:原式
18.;
【详解】解:原式
.
当时,原式.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
