第六章:实数练习题2021-2022学年福建省七年级下学期人教版数学期末试题选编(含解析)
文档属性
| 名称 | 第六章:实数练习题2021-2022学年福建省七年级下学期人教版数学期末试题选编(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 473.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-18 08:41:02 | ||
图片预览




文档简介
第六章:实数
一、单选题
1.(2022春·福建南平·七年级统考期末)4 的算术平方根是( )
A.2 B.±2 C.16 D.±16
2.(2022春·福建龙岩·七年级统考期末)下列说法中,正确的是( )
A.是的算术平方根 B.是的算术平方根
C.9的平方根是 D.是9的一个平方根
3.(2022春·福建福州·七年级统考期末)把2个面积为5的正方形纸片沿着对角线剪开,拼成如图所示的一个大正方形纸片,那么大正方形纸片的边长大小在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
4.(2022春·福建厦门·七年级统考期末)用式子表示“4的平方根是”,正确的是( )
A. B. C. D.
5.(2022春·福建龙岩·七年级统考期末)2的平方根是( )
A. B. C.±2 D.2
6.(2022春·福建莆田·七年级统考期末)若2022的两个平方根是m和n,则的值是( )
A.0 B.2022 C. D.4044
7.(2022春·福建福州·七年级统考期末)下列说法正确的是( )
A.4的算术平方根为 B.的立方根是
C.的平方根是 D.9的平方根是
8.(2022春·福建厦门·七年级统考期末)下列各式中正确的是( )
A. B. C. D.
9.(2022春·福建厦门·七年级统考期末)下列实数中无理数是( )
A. B. C. D.
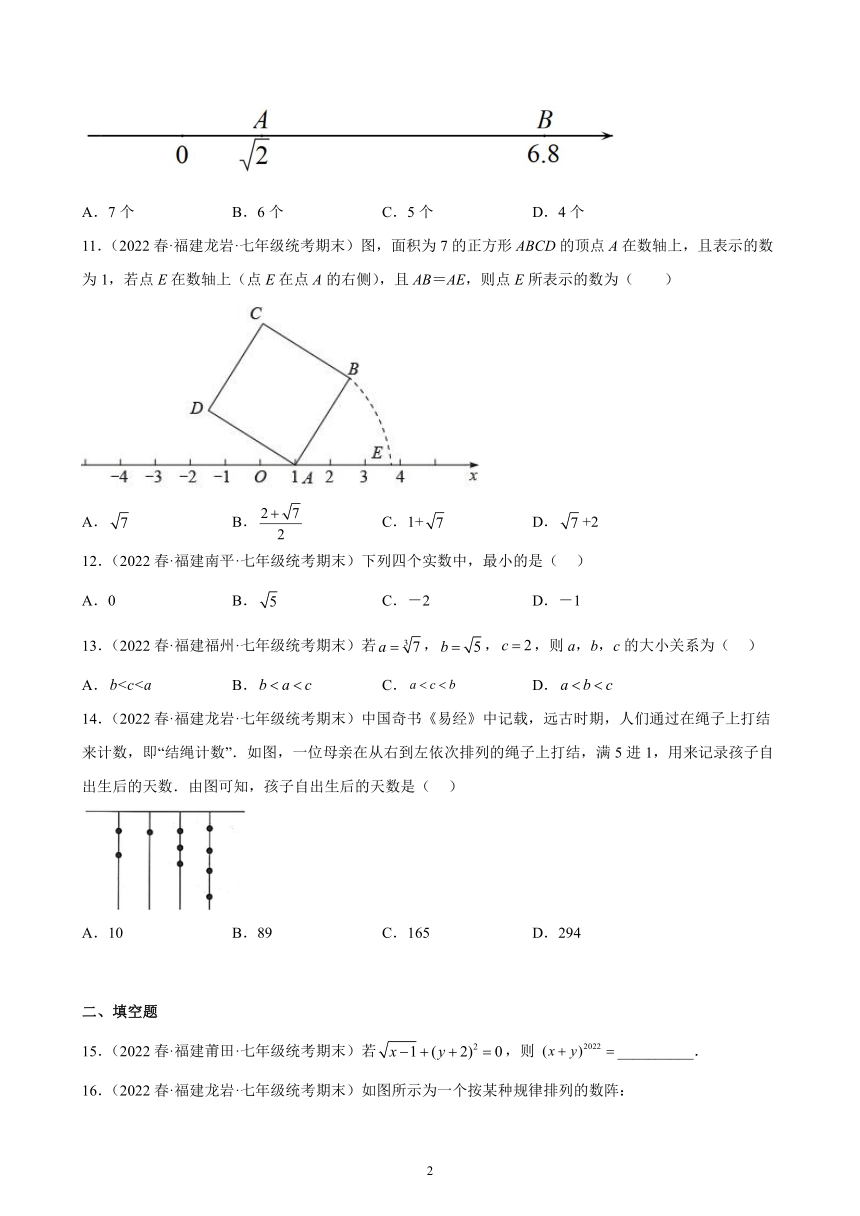
10.(2022春·福建莆田·七年级统考期末)如图,数轴上A,B两为表示的数分别为和6.8,则在点A和点B之间表示整数的点共有( )
A.7个 B.6个 C.5个 D.4个
11.(2022春·福建龙岩·七年级统考期末)图,面积为7的正方形ABCD的顶点A在数轴上,且表示的数为1,若点E在数轴上(点E在点A的右侧),且AB=AE,则点E所表示的数为( )
A. B. C.1+ D.+2
12.(2022春·福建南平·七年级统考期末)下列四个实数中,最小的是( )
A.0 B. C.-2 D.-1
13.(2022春·福建福州·七年级统考期末)若,,,则a,b,c的大小关系为( )
A. B. C. D.
14.(2022春·福建龙岩·七年级统考期末)中国奇书《易经》中记载,远古时期,人们通过在绳子上打结来计数,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满5进1,用来记录孩子自出生后的天数.由图可知,孩子自出生后的天数是( )
A.10 B.89 C.165 D.294
二、填空题
15.(2022春·福建莆田·七年级统考期末)若,则__________.
16.(2022春·福建龙岩·七年级统考期末)如图所示为一个按某种规律排列的数阵:
第1行 1
第2行 2
第3行 3
第4行 4
…… ……
根据数阵的规律,第8行倒数第二个数是___________.
17.(2022春·福建厦门·七年级统考期末)(1)若,那么______.(2)若,则______.
18.(2022春·福建厦门·七年级统考期末)计算下列各题:
(1)______;(2)______;(3)______;(4)______.
19.(2022春·福建福州·七年级统考期末)已知表示取三个数中最小的数.例如:当时,,当时,则______.
20.(2022春·福建龙岩·七年级统考期末)数轴上A,两点表示的数分别是和,则,两点间表示的整数的点共有______ 个.
三、解答题
21.(2022春·福建福州·七年级统考期末)计算:.
22.(2022春·福建福州·七年级统考期末)某学校有一块长、宽分别为38m和16m的长方形空地,计划沿边建造一个长宽之比为且面积为的长方形标准篮球场,请判断该学校能否用这块长方形空地建造符合要求的篮球场?并说明理由.
23.(2022春·福建福州·七年级统考期末)计算:
24.(2022春·福建厦门·七年级统考期末)数学家华罗庚在一次出国访问途中,看到飞机上的乘客阅读的杂志上有道智力题:求59319的立方根,华罗庚脱口而出“39”,邻座的乘客十分惊奇,忙问其中的奥妙.你知道怎样迅速地求出计算结果吗?请你按下面的步骤试一试.
第一步:∵,,且1000<59319<1000000
∴,即59319的立方根是一个两位数.
第二步:∵59319的个位数字是9,而.
∴能确定的个位数字是9.
第三步:如果划除59319后面的三位数,得到数59,而27<59<64.
∴,可得.
∴59319的立方根的十位数字是3.
∴59319的立方根是39.
根据上面的材料解答下面的问题:
(1)填空:1728的立方根是一个______位数,其个位数字是______;
(2)仿照上面的方法求157464的立方根a,并验证a是157464的立方根.
25.(2022春·福建福州·七年级统考期末)计算:.
26.(2022春·福建南平·七年级统考期末)计算:.
27.(2022春·福建莆田·七年级统考期末)如图为一个数值转换器.
(1)若输入的x值为3,则输出的y值为________;若输入的x值为9,则输出的y值为________;
(2)若输入x值后,经过两次取算术平方根运算,输出的y值为,求输入的x的值.
(3)尚进同学输入非负数x值后,却始终输不出y值.请你分析,他输入的x值是_______.
28.(2022秋·福建厦门·七年级统考期末)某小区在抗击新冠肺炎期间,为居民设计了一种身份识别图案.即在4×4的正方形网格中,白色正方形表示数字1,黑色正方形表示数字0,将第行第列表示的数记为(其中,都是不大于4的正整数),对第行使用公式进行计算,所得结果分别表示居民楼号、单元号、楼层和房间号.
(1)图1是居民甲的身份识别图案,.,说明居民甲居住在11号楼.试问图2中,______;居民甲居住在_______单元;
(2)若居民乙住在9号楼2单元4层01号,请借助图9画出其身份识别图案即可.
参考答案:
1.A
【分析】试题分析:利用算术平方根的定义计算即可得到结果.
【详解】解:∵22=4,
∴4的算术平方根是2.
故选:A.
2.D
【分析】根据平方根、算术平方根的定义解答即可.
【详解】解:A、3是(-3)2的算术平方根,故此选项不符合题意;
B、3是(-3)2的算术平方根,故此选项不符合题意;
C、9的平方根是±3,故此选项不符合题意;
D、-3是9的一个平方根,正确,故此选项符合题意;
故选:D.
【点睛】本题考查平方根,算术平方根的概念,掌握相关定义,注意符号是解题关键.
3.C
【分析】算出大正方形面积,利用正方形的面积等于边长的平方,判断边长的范围.
【详解】大正方形面积为,
,
故选:C.
【点睛】本题利用正方形的面积进行计算,也可以理解为对的值的范围的判断.
4.D
【分析】根据的平方根是求出即可.
【详解】解:4的平方根是,用数学式子表示为:,
故答案为:D.
【点睛】本题考查平方根,主要考查学生的理解能力和计算能力.
5.B
【分析】直接利用平方根的定义求解即可.
【详解】解:的平方根是,
故选:B.
【点睛】本题考查了平方根的定义,解题关键是牢记平方根的定义,其中一个正数的平方根有两个,它们互为相反数.
6.C
【分析】根据平方根的定义即可求解,正数的平方根互为相反数.
【详解】解:∵2022的两个平方根是m和n,
∴
故选:C
【点睛】本题考查了平方根的定义,掌握平方根的定义是解题的关键,平方根:如果x2=a,则x叫做a的平方根,记作“±”.
7.D
【分析】根据平方根定义、立方根定义、算术平方根定义进行判断即可.
【详解】A.4的算术平方根为2,故A错误;
B.的立方根是,故B错误;
C.的平方根是,故C错误;
D.9的平方根是,故D正确;
故选:D.
【点睛】本题主要考查了平方根、算术平方根和立方根的定义,熟练掌握一个正数的平方根有2个,一个数的立方根有一个,是解题的关键.
8.D
【分析】根据平方根、算术平方根和立方根的意义逐个判断即可.
【详解】解:A、,故A选项错误;
B、,故B选项错误;
C、∵,∴无意义,故C选项错误;
D、,故D选项正确,
故选:D.
【点睛】本题考查了平方根、算术平方根和立方根的意义,熟练掌握平方根、算术平方根和立方根的意义是解决本题的关键,尤其要注意平方根与算术平方根的区别与联系.
9.A
【分析】无限不循环小数叫做无理数,根据无理数的概念进行解答即可.
【详解】解:A.是开方开不尽的数,是无理数,故选项符合题意;
B.是分数,属于有理数,故选项不符合题意;
C.是无限循环小数,是有理数,故选项不符合题意;
D.=﹣3,是有理数,故选项不符合题意.
故选:A.
【点睛】此题考查的是无理数,熟知无理数的定义是解答此题的关键.
10.C
【分析】根据无理数的估算、结合数轴求解即可
【详解】解:∵
∴在到6.8之间有2,3,4,5,6这5个整数
故选C.
【点睛】本题考查了无理数的估算、实数与数轴,掌握无理数的估算方法是解题关键.
11.C
【分析】因为面积为7的正方形ABCD边长为,所以AB=,而AB=AE,得AE=,A点的坐标为1,故E点的坐标为+1.
【详解】∵面积为7的正方形ABCD为7,
∴AB=,
∵AB=AE,
∴AE=,
∵A点表示的数为1,
∴E点表示的数为+1,
故选:C.
【点睛】本题考查了数轴与实数、平方根的应用,关键是结合题意求出AB=AE=.
12.C
【分析】由于正数大于0,0大于负数,再利用两个负数比较大小,绝对值大的反而小,可求出最小值.
【详解】,
这四个数按照从小到大排序为:,
最小的是,
故选:C.
【点睛】本题主要考查实数大小的比较,掌握两个负数大小的比较方法是解题的关键.
13.C
【分析】根据无理数的估算进行大小比较.
【详解】解:∵,
又∵,
∴
故选:C.
【点睛】本题考查求一个数的算术平方根,求一个数的立方根及无理数的估算,理解相关概念是解题关键.
14.D
【分析】类比十进制“满十进一”,可以表示满5进1的数从左到右依次为:2×5×5×5,1×5×5,3×5,4,然后把它们相加即可.
【详解】依题意,还在自出生后的天数是:
2×5×5×5+1×5×5+3×5+4=250+25+15+4=294,
故选:D.
【点睛】本题考查了实数运算的实际应用,解答的关键是运用类比的方法找出满5进1的规律列式计算.
15.1
【分析】根据算术平方根的非负性、偶次方的非负性求出x、y,计算即可.
【详解】解:∵(y+2)2=0,0,(y+2)2≥0,
∴x﹣1=0,y+2=0,
解得:x=1,y=﹣2,
则(x+y)2022=(﹣1)2022=1,
故答案为:1.
【点睛】本题考查的是非负数的性质,掌握二次根式的被开方数是非负数、偶次方的非负性是解题的关键.
16.
【分析】根据数阵的规律可知:被开方数是连续的正整数,根据每一行的最后一个数的被开方数是所在的行数乘比行数大1的数,可得结论.
【详解】第1行的最后一个数是,
第2行的最后一个数是,
第3行的最后一个数是,
……
第8行最后一个数字为,
∴第8行倒数第二个数是,
故答案为:.
【点睛】本题考查了数字的变化,算术平方根,观察题目找出解题点是解题的关键.
17. ±9 4
【分析】(1)根据平方根的定义进行求解即可;
(2)根据算术平方根进行求解即可.
【详解】(1)解:∵(±9)2=81,
∴x==±9;
故答案为:±9
(2)解:∵,
∴,
∴x=4.
故答案为:4
【点睛】此题考查了平方根和算术平方根,熟练掌握平方根和算术平方根的定义是解题的关键.
18. 3 ##
【分析】根据算术平方根的定义、立方根的定义、绝对值的意义进行计算即可.
【详解】解:(1);
(2);
(3);
(4).
故答案为:3;;;.
【点睛】本题主要考查了算术平方根、立方根和绝对值的计算,解题的关键是熟练掌握算术平方根的定义、立方根的定义、绝对值的意义,准确计算.
19.
【分析】比较、、的大小,最小的等于,在求出的值即可.
【详解】解:由题意可知的取值范围是,
①当0②当x≥1时,,此时,x=不符合题意舍去.
∴x=,
故答案为:.
【点睛】本题考查了实数的大小比较,算术平方根及其最值问题,解此类题关键要注意分类思想的运用.
20.4
【分析】首先分别估算出和的大小,然后根据数轴的特征,判断出A,两点间表示的整数的点共有多少个即可.
【详解】解:,,
∴A,两点间表示的整数的点共有个:、、、.
故答案为:.
【点睛】此题主要考查了实数与数轴问题,要熟练掌握,解答此题的关键是要明确:实数与数轴上的点是一一对应关系.任意一个实数都可以用数轴上的点表示;反之,数轴上的任意一个点都表示一个实数.数轴上的任一点表示的数,不是有理数,就是无理数.
此题还考查了估算无理数的大小的方法,要熟练掌握
21.
【分析】由绝对值、乘方、算术平方根的运算法则进行计算,即可求出答案.
【详解】解:原式
;
【点睛】本题考查了绝对值、乘方、算术平方根的运算法则,解题的关键是掌握运算法则,正确的进行化简.
22.不能,理由见解析
【分析】通过用同一未知数表示出篮球场的长和宽,列方程进行求解.
【详解】解:不能,理由如下:
设长方形标准篮球场的长为5x m.宽为3x m,
由题意得:5x×3x=540,
解得:x= 6(舍去)或6,
即长方形标准篮球场的长为30m,宽为18m,
∵18m>16m,
∴该学校不能用这块长方形空地建造符合要求的篮球场.
【点睛】此题主要考查了算术平方根,正确得出x的值是解题的关键.
23.
【分析】根据立方根的计算,绝对值的化简计算即可.
【详解】
.
【点睛】本题考查了实数的运算,立方根的计算,绝对值的化简,熟练掌握运算法则是解题的关键.
24.(1)两;2
(2)a=54
【分析】(1)根据上面的材料所给的方法确定1728的立方根的位数及个位数字即可.
(2)仿照上面材料所给的方法先确定a的位数,再确定个位数字,再确定十位数字即可求出a的值.
【详解】(1)解:∵,,且1000<1728<1000000
∴,即1728的立方根是一个两位数.
∵1728的个位数字是8,而,
∴能确定的个位数字是2.
故答案为:两,2
(2)解:∵,,且1000<157464<1000000
∴,即157464的立方根是一个两位数.
∵157464的个位数字是4,而,
∴能确定的个位数字是4.
如果划除157464后面的三位数,得到数157,而125<157<216.
∴,可得.
∴157464的立方根的十位数字是5.
∴157464的立方根是54.
即a=54
经过验证
【点睛】本题主要考查了学生的阅读理解能力,能够读懂材料并能熟练计算1-10的立方是解题的关键.
25.
【分析】根据算术平方根、立方根和绝对值的性质计算即可.
【详解】解:
【点睛】本题考查了实数运算,熟练掌握算术平方根、立方根和绝对值的性质是解题关键.
26.
【分析】根据绝对值的性质、立方根及二次根式的性质进行化简,再按照从左到右的顺序进行计算即可.
【详解】解:原式=
=
【点睛】本题考查了实数的混合运算,涉及绝对值的性质、立方根及二次根式的性质,熟练掌握运算法则是解题的关键.
27.(1)
(2)36
(3)0或1
【分析】(1)根据运算规则即可求解;
(2)根据两次取算术平方根运算,输出的y值为,返回运算两次平方可得x的值;
(3)根据0和1的算术平方根分别是0和1,可得结论.
【详解】(1)当时,取算术平方根为,为无理数,则输出的y值为;
当,取算术平方根为3,3 是有理数,继续计算,取算术平方根为,为无理数,则输出的y值为;
故答案为:,
(2)当时,,,
则
(3)当x=0,1时,始终输不出y值,
∵0,1的算术平方根是0,1,一定是有理数,
∴他输入的x值是0或1.
故答案为:0或1.
【点睛】本题考查了程序与实数计算,理解题意是解题的关键.
28.(1)0;2
(2)见解析
【分析】(1)根据白色正方形表示数字1,黑色正方形表示数字0,第行第列表示的数记为,观察图形可得答案,按题中公式计算即可;
(2)按题中公式及9号楼2单元4层01号画图即可.
(1)
根据题意,表示第四行第一个,为黑色,黑色表示0,从而得出
则居民甲居住在2单元
故答案为:0,2;
(2)
9号楼2单元4层01号居民的身份识别图案如图:
A1=1×23+0×22+0×2+1×1=8+1=9
A2=0×23+0×22+1×2+0×1=2,
A3=0×33+1×22+0×2+0×1=4,
A4=0×23+0×22+0×2+1×1=1,
【点睛】本题考查实数与图形,理解题意,将所求问题转化为实数运算时解题的关键.
一、单选题
1.(2022春·福建南平·七年级统考期末)4 的算术平方根是( )
A.2 B.±2 C.16 D.±16
2.(2022春·福建龙岩·七年级统考期末)下列说法中,正确的是( )
A.是的算术平方根 B.是的算术平方根
C.9的平方根是 D.是9的一个平方根
3.(2022春·福建福州·七年级统考期末)把2个面积为5的正方形纸片沿着对角线剪开,拼成如图所示的一个大正方形纸片,那么大正方形纸片的边长大小在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
4.(2022春·福建厦门·七年级统考期末)用式子表示“4的平方根是”,正确的是( )
A. B. C. D.
5.(2022春·福建龙岩·七年级统考期末)2的平方根是( )
A. B. C.±2 D.2
6.(2022春·福建莆田·七年级统考期末)若2022的两个平方根是m和n,则的值是( )
A.0 B.2022 C. D.4044
7.(2022春·福建福州·七年级统考期末)下列说法正确的是( )
A.4的算术平方根为 B.的立方根是
C.的平方根是 D.9的平方根是
8.(2022春·福建厦门·七年级统考期末)下列各式中正确的是( )
A. B. C. D.
9.(2022春·福建厦门·七年级统考期末)下列实数中无理数是( )
A. B. C. D.
10.(2022春·福建莆田·七年级统考期末)如图,数轴上A,B两为表示的数分别为和6.8,则在点A和点B之间表示整数的点共有( )
A.7个 B.6个 C.5个 D.4个
11.(2022春·福建龙岩·七年级统考期末)图,面积为7的正方形ABCD的顶点A在数轴上,且表示的数为1,若点E在数轴上(点E在点A的右侧),且AB=AE,则点E所表示的数为( )
A. B. C.1+ D.+2
12.(2022春·福建南平·七年级统考期末)下列四个实数中,最小的是( )
A.0 B. C.-2 D.-1
13.(2022春·福建福州·七年级统考期末)若,,,则a,b,c的大小关系为( )
A. B. C. D.
14.(2022春·福建龙岩·七年级统考期末)中国奇书《易经》中记载,远古时期,人们通过在绳子上打结来计数,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满5进1,用来记录孩子自出生后的天数.由图可知,孩子自出生后的天数是( )
A.10 B.89 C.165 D.294
二、填空题
15.(2022春·福建莆田·七年级统考期末)若,则__________.
16.(2022春·福建龙岩·七年级统考期末)如图所示为一个按某种规律排列的数阵:
第1行 1
第2行 2
第3行 3
第4行 4
…… ……
根据数阵的规律,第8行倒数第二个数是___________.
17.(2022春·福建厦门·七年级统考期末)(1)若,那么______.(2)若,则______.
18.(2022春·福建厦门·七年级统考期末)计算下列各题:
(1)______;(2)______;(3)______;(4)______.
19.(2022春·福建福州·七年级统考期末)已知表示取三个数中最小的数.例如:当时,,当时,则______.
20.(2022春·福建龙岩·七年级统考期末)数轴上A,两点表示的数分别是和,则,两点间表示的整数的点共有______ 个.
三、解答题
21.(2022春·福建福州·七年级统考期末)计算:.
22.(2022春·福建福州·七年级统考期末)某学校有一块长、宽分别为38m和16m的长方形空地,计划沿边建造一个长宽之比为且面积为的长方形标准篮球场,请判断该学校能否用这块长方形空地建造符合要求的篮球场?并说明理由.
23.(2022春·福建福州·七年级统考期末)计算:
24.(2022春·福建厦门·七年级统考期末)数学家华罗庚在一次出国访问途中,看到飞机上的乘客阅读的杂志上有道智力题:求59319的立方根,华罗庚脱口而出“39”,邻座的乘客十分惊奇,忙问其中的奥妙.你知道怎样迅速地求出计算结果吗?请你按下面的步骤试一试.
第一步:∵,,且1000<59319<1000000
∴,即59319的立方根是一个两位数.
第二步:∵59319的个位数字是9,而.
∴能确定的个位数字是9.
第三步:如果划除59319后面的三位数,得到数59,而27<59<64.
∴,可得.
∴59319的立方根的十位数字是3.
∴59319的立方根是39.
根据上面的材料解答下面的问题:
(1)填空:1728的立方根是一个______位数,其个位数字是______;
(2)仿照上面的方法求157464的立方根a,并验证a是157464的立方根.
25.(2022春·福建福州·七年级统考期末)计算:.
26.(2022春·福建南平·七年级统考期末)计算:.
27.(2022春·福建莆田·七年级统考期末)如图为一个数值转换器.
(1)若输入的x值为3,则输出的y值为________;若输入的x值为9,则输出的y值为________;
(2)若输入x值后,经过两次取算术平方根运算,输出的y值为,求输入的x的值.
(3)尚进同学输入非负数x值后,却始终输不出y值.请你分析,他输入的x值是_______.
28.(2022秋·福建厦门·七年级统考期末)某小区在抗击新冠肺炎期间,为居民设计了一种身份识别图案.即在4×4的正方形网格中,白色正方形表示数字1,黑色正方形表示数字0,将第行第列表示的数记为(其中,都是不大于4的正整数),对第行使用公式进行计算,所得结果分别表示居民楼号、单元号、楼层和房间号.
(1)图1是居民甲的身份识别图案,.,说明居民甲居住在11号楼.试问图2中,______;居民甲居住在_______单元;
(2)若居民乙住在9号楼2单元4层01号,请借助图9画出其身份识别图案即可.
参考答案:
1.A
【分析】试题分析:利用算术平方根的定义计算即可得到结果.
【详解】解:∵22=4,
∴4的算术平方根是2.
故选:A.
2.D
【分析】根据平方根、算术平方根的定义解答即可.
【详解】解:A、3是(-3)2的算术平方根,故此选项不符合题意;
B、3是(-3)2的算术平方根,故此选项不符合题意;
C、9的平方根是±3,故此选项不符合题意;
D、-3是9的一个平方根,正确,故此选项符合题意;
故选:D.
【点睛】本题考查平方根,算术平方根的概念,掌握相关定义,注意符号是解题关键.
3.C
【分析】算出大正方形面积,利用正方形的面积等于边长的平方,判断边长的范围.
【详解】大正方形面积为,
,
故选:C.
【点睛】本题利用正方形的面积进行计算,也可以理解为对的值的范围的判断.
4.D
【分析】根据的平方根是求出即可.
【详解】解:4的平方根是,用数学式子表示为:,
故答案为:D.
【点睛】本题考查平方根,主要考查学生的理解能力和计算能力.
5.B
【分析】直接利用平方根的定义求解即可.
【详解】解:的平方根是,
故选:B.
【点睛】本题考查了平方根的定义,解题关键是牢记平方根的定义,其中一个正数的平方根有两个,它们互为相反数.
6.C
【分析】根据平方根的定义即可求解,正数的平方根互为相反数.
【详解】解:∵2022的两个平方根是m和n,
∴
故选:C
【点睛】本题考查了平方根的定义,掌握平方根的定义是解题的关键,平方根:如果x2=a,则x叫做a的平方根,记作“±”.
7.D
【分析】根据平方根定义、立方根定义、算术平方根定义进行判断即可.
【详解】A.4的算术平方根为2,故A错误;
B.的立方根是,故B错误;
C.的平方根是,故C错误;
D.9的平方根是,故D正确;
故选:D.
【点睛】本题主要考查了平方根、算术平方根和立方根的定义,熟练掌握一个正数的平方根有2个,一个数的立方根有一个,是解题的关键.
8.D
【分析】根据平方根、算术平方根和立方根的意义逐个判断即可.
【详解】解:A、,故A选项错误;
B、,故B选项错误;
C、∵,∴无意义,故C选项错误;
D、,故D选项正确,
故选:D.
【点睛】本题考查了平方根、算术平方根和立方根的意义,熟练掌握平方根、算术平方根和立方根的意义是解决本题的关键,尤其要注意平方根与算术平方根的区别与联系.
9.A
【分析】无限不循环小数叫做无理数,根据无理数的概念进行解答即可.
【详解】解:A.是开方开不尽的数,是无理数,故选项符合题意;
B.是分数,属于有理数,故选项不符合题意;
C.是无限循环小数,是有理数,故选项不符合题意;
D.=﹣3,是有理数,故选项不符合题意.
故选:A.
【点睛】此题考查的是无理数,熟知无理数的定义是解答此题的关键.
10.C
【分析】根据无理数的估算、结合数轴求解即可
【详解】解:∵
∴在到6.8之间有2,3,4,5,6这5个整数
故选C.
【点睛】本题考查了无理数的估算、实数与数轴,掌握无理数的估算方法是解题关键.
11.C
【分析】因为面积为7的正方形ABCD边长为,所以AB=,而AB=AE,得AE=,A点的坐标为1,故E点的坐标为+1.
【详解】∵面积为7的正方形ABCD为7,
∴AB=,
∵AB=AE,
∴AE=,
∵A点表示的数为1,
∴E点表示的数为+1,
故选:C.
【点睛】本题考查了数轴与实数、平方根的应用,关键是结合题意求出AB=AE=.
12.C
【分析】由于正数大于0,0大于负数,再利用两个负数比较大小,绝对值大的反而小,可求出最小值.
【详解】,
这四个数按照从小到大排序为:,
最小的是,
故选:C.
【点睛】本题主要考查实数大小的比较,掌握两个负数大小的比较方法是解题的关键.
13.C
【分析】根据无理数的估算进行大小比较.
【详解】解:∵,
又∵,
∴
故选:C.
【点睛】本题考查求一个数的算术平方根,求一个数的立方根及无理数的估算,理解相关概念是解题关键.
14.D
【分析】类比十进制“满十进一”,可以表示满5进1的数从左到右依次为:2×5×5×5,1×5×5,3×5,4,然后把它们相加即可.
【详解】依题意,还在自出生后的天数是:
2×5×5×5+1×5×5+3×5+4=250+25+15+4=294,
故选:D.
【点睛】本题考查了实数运算的实际应用,解答的关键是运用类比的方法找出满5进1的规律列式计算.
15.1
【分析】根据算术平方根的非负性、偶次方的非负性求出x、y,计算即可.
【详解】解:∵(y+2)2=0,0,(y+2)2≥0,
∴x﹣1=0,y+2=0,
解得:x=1,y=﹣2,
则(x+y)2022=(﹣1)2022=1,
故答案为:1.
【点睛】本题考查的是非负数的性质,掌握二次根式的被开方数是非负数、偶次方的非负性是解题的关键.
16.
【分析】根据数阵的规律可知:被开方数是连续的正整数,根据每一行的最后一个数的被开方数是所在的行数乘比行数大1的数,可得结论.
【详解】第1行的最后一个数是,
第2行的最后一个数是,
第3行的最后一个数是,
……
第8行最后一个数字为,
∴第8行倒数第二个数是,
故答案为:.
【点睛】本题考查了数字的变化,算术平方根,观察题目找出解题点是解题的关键.
17. ±9 4
【分析】(1)根据平方根的定义进行求解即可;
(2)根据算术平方根进行求解即可.
【详解】(1)解:∵(±9)2=81,
∴x==±9;
故答案为:±9
(2)解:∵,
∴,
∴x=4.
故答案为:4
【点睛】此题考查了平方根和算术平方根,熟练掌握平方根和算术平方根的定义是解题的关键.
18. 3 ##
【分析】根据算术平方根的定义、立方根的定义、绝对值的意义进行计算即可.
【详解】解:(1);
(2);
(3);
(4).
故答案为:3;;;.
【点睛】本题主要考查了算术平方根、立方根和绝对值的计算,解题的关键是熟练掌握算术平方根的定义、立方根的定义、绝对值的意义,准确计算.
19.
【分析】比较、、的大小,最小的等于,在求出的值即可.
【详解】解:由题意可知的取值范围是,
①当0
∴x=,
故答案为:.
【点睛】本题考查了实数的大小比较,算术平方根及其最值问题,解此类题关键要注意分类思想的运用.
20.4
【分析】首先分别估算出和的大小,然后根据数轴的特征,判断出A,两点间表示的整数的点共有多少个即可.
【详解】解:,,
∴A,两点间表示的整数的点共有个:、、、.
故答案为:.
【点睛】此题主要考查了实数与数轴问题,要熟练掌握,解答此题的关键是要明确:实数与数轴上的点是一一对应关系.任意一个实数都可以用数轴上的点表示;反之,数轴上的任意一个点都表示一个实数.数轴上的任一点表示的数,不是有理数,就是无理数.
此题还考查了估算无理数的大小的方法,要熟练掌握
21.
【分析】由绝对值、乘方、算术平方根的运算法则进行计算,即可求出答案.
【详解】解:原式
;
【点睛】本题考查了绝对值、乘方、算术平方根的运算法则,解题的关键是掌握运算法则,正确的进行化简.
22.不能,理由见解析
【分析】通过用同一未知数表示出篮球场的长和宽,列方程进行求解.
【详解】解:不能,理由如下:
设长方形标准篮球场的长为5x m.宽为3x m,
由题意得:5x×3x=540,
解得:x= 6(舍去)或6,
即长方形标准篮球场的长为30m,宽为18m,
∵18m>16m,
∴该学校不能用这块长方形空地建造符合要求的篮球场.
【点睛】此题主要考查了算术平方根,正确得出x的值是解题的关键.
23.
【分析】根据立方根的计算,绝对值的化简计算即可.
【详解】
.
【点睛】本题考查了实数的运算,立方根的计算,绝对值的化简,熟练掌握运算法则是解题的关键.
24.(1)两;2
(2)a=54
【分析】(1)根据上面的材料所给的方法确定1728的立方根的位数及个位数字即可.
(2)仿照上面材料所给的方法先确定a的位数,再确定个位数字,再确定十位数字即可求出a的值.
【详解】(1)解:∵,,且1000<1728<1000000
∴,即1728的立方根是一个两位数.
∵1728的个位数字是8,而,
∴能确定的个位数字是2.
故答案为:两,2
(2)解:∵,,且1000<157464<1000000
∴,即157464的立方根是一个两位数.
∵157464的个位数字是4,而,
∴能确定的个位数字是4.
如果划除157464后面的三位数,得到数157,而125<157<216.
∴,可得.
∴157464的立方根的十位数字是5.
∴157464的立方根是54.
即a=54
经过验证
【点睛】本题主要考查了学生的阅读理解能力,能够读懂材料并能熟练计算1-10的立方是解题的关键.
25.
【分析】根据算术平方根、立方根和绝对值的性质计算即可.
【详解】解:
【点睛】本题考查了实数运算,熟练掌握算术平方根、立方根和绝对值的性质是解题关键.
26.
【分析】根据绝对值的性质、立方根及二次根式的性质进行化简,再按照从左到右的顺序进行计算即可.
【详解】解:原式=
=
【点睛】本题考查了实数的混合运算,涉及绝对值的性质、立方根及二次根式的性质,熟练掌握运算法则是解题的关键.
27.(1)
(2)36
(3)0或1
【分析】(1)根据运算规则即可求解;
(2)根据两次取算术平方根运算,输出的y值为,返回运算两次平方可得x的值;
(3)根据0和1的算术平方根分别是0和1,可得结论.
【详解】(1)当时,取算术平方根为,为无理数,则输出的y值为;
当,取算术平方根为3,3 是有理数,继续计算,取算术平方根为,为无理数,则输出的y值为;
故答案为:,
(2)当时,,,
则
(3)当x=0,1时,始终输不出y值,
∵0,1的算术平方根是0,1,一定是有理数,
∴他输入的x值是0或1.
故答案为:0或1.
【点睛】本题考查了程序与实数计算,理解题意是解题的关键.
28.(1)0;2
(2)见解析
【分析】(1)根据白色正方形表示数字1,黑色正方形表示数字0,第行第列表示的数记为,观察图形可得答案,按题中公式计算即可;
(2)按题中公式及9号楼2单元4层01号画图即可.
(1)
根据题意,表示第四行第一个,为黑色,黑色表示0,从而得出
则居民甲居住在2单元
故答案为:0,2;
(2)
9号楼2单元4层01号居民的身份识别图案如图:
A1=1×23+0×22+0×2+1×1=8+1=9
A2=0×23+0×22+1×2+0×1=2,
A3=0×33+1×22+0×2+0×1=4,
A4=0×23+0×22+0×2+1×1=1,
【点睛】本题考查实数与图形,理解题意,将所求问题转化为实数运算时解题的关键.
