第十章:数据的收集、整理与描述练习题2021-2022学年福建省七年级下学期人教版数学期末试题选编(含解析)
文档属性
| 名称 | 第十章:数据的收集、整理与描述练习题2021-2022学年福建省七年级下学期人教版数学期末试题选编(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 660.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-18 08:45:33 | ||
图片预览




文档简介
第十章:数据的收集、整理与描述
一、单选题
1.(2022春·福建龙岩·七年级统考期末)下列调查中,适合用普查的是( )
A.新冠疫情期间检测地铁乘客的体温
B.调查全中国中学生的近视率
C.调查某品牌电视机的使用寿命
D.调查长江中现有鱼的种类
2.(2022春·福建厦门·七年级统考期末)为了了解某初中学校学生的视力情况,需要抽取部分学生进行调查.下列抽取学生的方法最合适的是( )
A.随机抽取该校一个班级的学生 B.随机抽取该校一个年级的学生
C.随机抽取该校一部分男生 D.分别从该校初一、初二、初三年级中各随机抽取10%的学生
3.(2022春·福建厦门·七年级统考期末)某校全体学生中随机抽取部分学生进行问卷调查,了解每周的劳动时间,按平均劳动时间t(单位:h)分为四组:A组“t<5”,B组“5≤t<7”,C组“7≤t<9”,D组“t>9”.将收集到的数据整理后,绘制成两幅不完整的统计图,如图所示.则下列说法错误的是( )
A.本次接受问卷调查的学生有100人
B.在扇形统计图中,B组占比为45%
C.在扇形统计图中,C组所占圆心角的度数为108°
D.该校共有1500名学生,估计该校平均每周劳动时间不少于7h的学生人数为675人
4.(2022春·福建福州·七年级统考期末)为了直观了解我国近十年人口增长率的变化趋势,最适合使用的统计图是( )
A.条形图 B.折线图 C.扇形图 D.频数分布直方图
5.(2022春·福建福州·七年级统考期末)已知样本数据个数为30,且被分成4组,各组数据个数之比为2:3:4:1,则第二小组频数和第三小组的频率分别为( )
A.0.4和0.3 B.0.4和9 C.9和0.4 D.12和9
6.(2022春·福建龙岩·七年级统考期末)有40个数据,其中最大值为45,最小值为12,若取组距为5,对数据进行分组,则应分为( )
A.7组 B.6组 C.5组 D.4组
二、填空题
7.(2022秋·福建漳州·七年级统考期末)中国北斗卫星导航系统是中国自行研制的全球卫星导航系统.是继美国全球定位系统()、俄罗斯格洛纳斯卫星导航系统()之后第三个成熟的卫星导航系统.在发射前,对我国最后一颗北斗卫星各零部件的调查,最适合采用的调查方式是__________.(填“普查”或“抽样调查”)
8.(2022春·福建福州·七年级统考期末)如图,整个圆表示某班参加课外活动的总人数,跳绳的人数占30%,表示踢毽的扇形圆心角是60°,踢毽和打篮球的人数比是12,那么表示参加“其它”活动的人数占总人数的____%.
9.(2022春·福建厦门·七年级统考期末)记录某足球队全年比赛结果(“胜”、“负”、“平”)的条形统计图和扇形统计图(不完整)如下:
根据图中信息,该足球队全年比赛胜了_____场.
10.(2022春·福建福州·七年级统考期末)某小区五月份1日至5日每天用水量变化情况如图所示,那么这天中用水量最多的一天比最少的一天多_______吨
11.(2022春·福建厦门·七年级统考期末)如图是2018年参加PISA测试(国际学生评估项目)的79个国家学生的数学平均成绩(x)的3个统计图,能最直观地说明一半以上国家的学生成绩在60≤x<70之间的统计图是 _____.(填“直方图”,“扇形统计图”,“折线统计图”)
12.(2022春·福建福州·七年级统考期末)体育老师从七年级学生中抽取40名参加全校的健身操比赛.这些学生身高(单位:)的最大值为186,最小值为155.若取组距为3,则可以分成__________组.
13.(2022春·福建莆田·七年级统考期末)某中学积极开展体育锻炼,一次跳绳活动后,七年一班体育委员统计了全班1分钟跳绳的次数,其中次数最多为216,最少为62.若取组距为20,则可以分成__________组.
14.(2022春·福建厦门·七年级统考期末)某中学九年级甲、乙两个班参加了一次数学考试,考试人数每班都为40人,每个班的考试成绩分为A、B、C、D、E五个等级,绘制的统计图如下:
根据以上统计图提供的信息,则D等级这一组人数较多的班是________
三、解答题
15.(2022春·福建莆田·七年级统考期末)2022年3月23日“天宫课堂”第二课在中国空间站正式开讲,“太空教师”翟志刚、王亚平、叶光富再次给大家带来一堂精彩的太空科普课.某校组织全校学生同步观看,直播结束后,教务处随机抽取了名学生,将他们最喜欢的太空实验分成四组,组:太空“冰雪”实验;B组:液桥演示实验;C组:水油分离实验;D组:太空抛物实验,并得到如下不完整的统计图表.请利用统计图表提供的信息回答下列问题:
学生最喜欢的太空实验人数统计表
分组 A组 B组 C组 D组
人数 a 15 20 b
(1)________,________,________;
(2)补全条形统计图;
(3)若全校同步观看直播的学生共有800人,请估计该校最喜欢太空抛物实验的人数.
16.(2022春·福建南平·七年级统考期末)2022年北京成功举办了第24届冬季奥林匹克运动会.为了调查同学们对冬奥知识的了解情况,某学校组织了“冬奥知识知多少”竞赛活动,随机抽取了部分学生的竞赛成绩进行分析,共分为四个等级:A,B,C,D,并绘制了如下不完整的统计图.请结合统计图表,回答下列问题:
(1)本次抽样的学生人数为多少人?
(2)扇形统计图中“C等级”所在扇形的圆心角是多少度?
(3)若该校共有学生3000人,请估计该校学生对冬奥知识了解情况的程度为“A和B等级”的学生约有多少人?
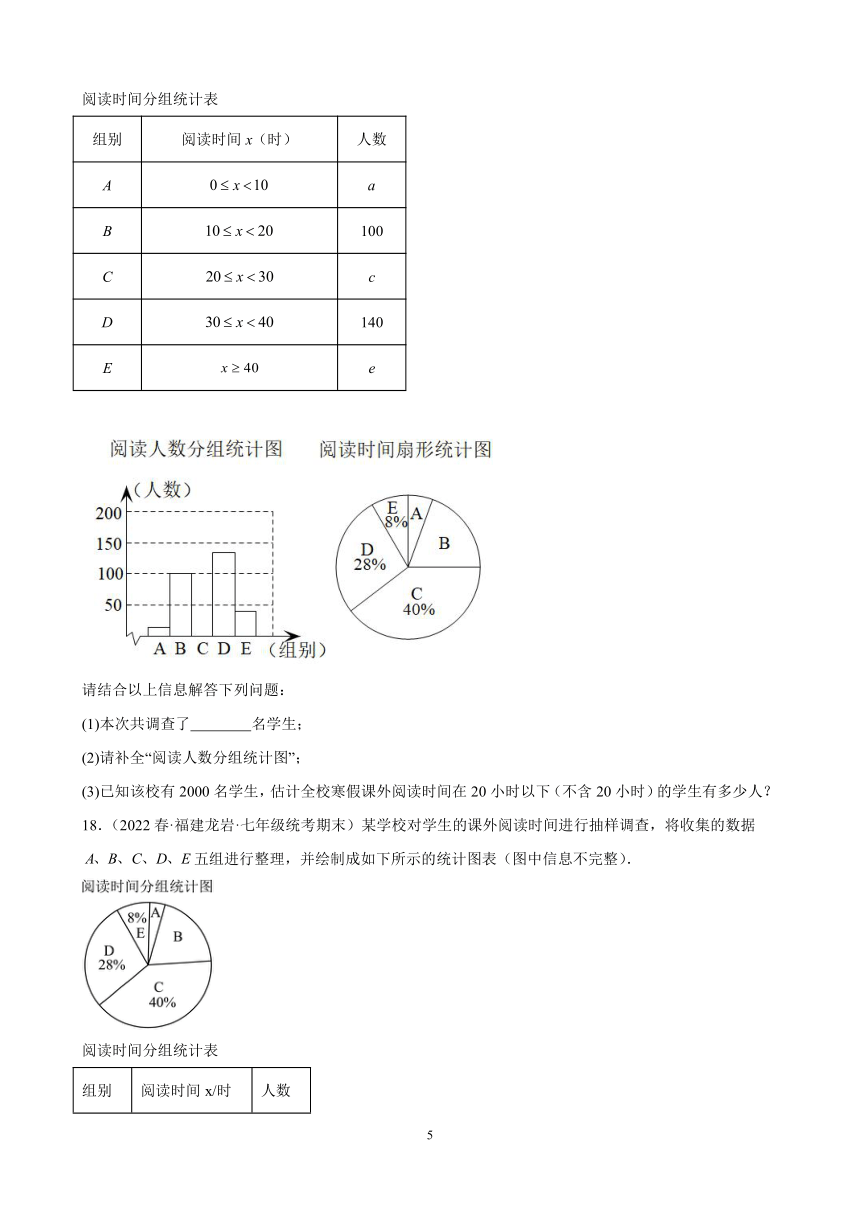
17.(2022春·福建厦门·七年级统考期末)某学校对学生寒假课外阅读时间进行抽样调查,将收集的数据分成A,B,C,D,E五组进行整理,并绘制成如下的统计图表(图中信息不完整).
阅读时间分组统计表
组别 阅读时间x(时) 人数
A a
B 100
C c
D 140
E e
请结合以上信息解答下列问题:
(1)本次共调查了 名学生;
(2)请补全“阅读人数分组统计图”;
(3)已知该校有2000名学生,估计全校寒假课外阅读时间在20小时以下(不含20小时)的学生有多少人?
18.(2022春·福建龙岩·七年级统考期末)某学校对学生的课外阅读时间进行抽样调查,将收集的数据五组进行整理,并绘制成如下所示的统计图表(图中信息不完整).
阅读时间分组统计表
组别 阅读时间x/时 人数
A a
B 100
C b
D 140
E c
请结合以上信息解答下列问题:
(1)求的值;
(2)求扇形统计图中B的圆心角的度数;
(3)估计全校课外阅读时间在20小时以下(不含20小时)的学生所占的比例.
19.(2022春·福建龙岩·七年级统考期末)022年3月23日下午,中国空间站“天宫课堂”再度开课,“太空教师”翟志刚、王亚平、叶光富演示了太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验.某校学生全员观看了太空授课直播,为了了解学生心中“最受启发的实验”的情况,随机抽取了部分学生(每人只选择一个实验)进行调查,以下是根据调查结果绘制的统计图表的一部分.
最受启发的实验 频数(人) 频率
A.“冰雪”实验 6 0.15
B.液桥演示实验
C.水油分离实验
D.太空抛物实验 0.35
根据以上信息,回答下列问题:
(1)被调查的学生中,认为最受启发的实验是A的学生人数为______人,认为最受启发的实验是C的学生人数占被调查学生总人数的百分比为______%;
(2)本次调查的样本容量为______,样本中认为最受启发的实验是D的学生人数为______人;
(3)若该校共有1200名学生,请根据调查结果,估计认为最受启发的实验是B的学生人数.
20.(2022春·福建厦门·七年级统考期末)2020年是脱贫攻坚年,为实现全员脱贫目标,某村贫困户在当地政府支持帮助下,办起了养鸡场,经过一段时间精心饲养,总量为3000只的一批鸡可以出售.现从中随机抽取50只,得到它们质量的统计数据如下:
质量 组中值 数量(只)
1.0 6
1.2 9
1.4 a
1.6 15
1.8 8
根据以上信息,解答下列问题:
(1)表中______,补全频数分布直方图;
(2)这批鸡中质量不小于的大约有多少只?
(3)这些贫困户的总收入达到54000元,就能实现全员脱贫目标.按15元的价格售出这批鸡后,该村贫困户能否脱贫?
21.(2022春·福建福州·七年级统考期末)某学校环保志者协会对该市城区的空气质量进行调查,从全年365天中随机抽取了80天的空气质量指数(AQI)数据,绘制出三幅不完整的统计图表.请根据图表中提供的信息解答下列问题:
AQI指数 质量等级 天数(天)
0-50 优
51-100 良 44
101-150 轻度污染
151-200 中度污染 4
201-300 重度污染 2
300以上 严重污染 2
(1)统计表中m=______,n=______.扇形统计图中,空气质量等级为“良”的天数占_____%;
(2)补全直方图,并通过计算估计该市城区的空气质量等级为“中度污染”和“重度污染”的天数共多少天?(结果保留整数)
参考答案:
1.A
【分析】根据全面调查和抽样调查的概念解答.
【详解】解:A、新冠疫情期间检测地铁乘客的体温,适合用普查;
B、调查全中国中学生的近视率,适合用抽查;
C、调查某品牌电视机的使用寿命,适合用抽查;
D、调查长江中现有鱼的种类,适合用抽查;
故选:A.
【点睛】本题考查的是全面调查和抽样调查,通过普查可以直接得到较为全面、可靠的信息,但花费的时间较长,耗费大,且一些调查项目并不适合普查.其一,调查者能力有限,不能进行普查.其二,调查过程带有破坏性.其三,有些被调查的对象无法进行普查.
2.D
【详解】因为要了解初中的视力情况范围较大、难度较大,所以应采取抽样调查的方法比较合适,本题考查的是调查方法的选择,正确选择调查方式要根据全面调查的优缺点再结合实际情况去分析,故只有D符合实际并具有普遍性,故选D.
3.D
【分析】根据C组的人数和所占的百分比求出调查的总人数,用B组的人数除以总人数求出B所占的百分比,用360°乘以C组所占的百分比,求出C组所占圆心角的度数,再用该校的总人数乘以该校平均每周劳动时间不少于7h的学生人数所占的百分比即可得出答案.
【详解】解:A、本次接受问卷调查的学生有30÷30%=100(人),故本选项正确,不符合题意;
B、在扇形统计图中,B组占比为×100%=45%,故本选项正确,不符合题意;
C、在扇形统计图中,C组所占圆心角的度数为:360°×=108°,故本选项正确,不符合题意;
D、该校共有1500名学生,估计该校平均每周劳动时间不少于7h的学生人数:1500×=600(人),故本选项错误,符合题意;
故选:D.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
4.B
【分析】由扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目,据此可得答案.
【详解】解:为了直观了解我国近十年人口增长率的变化趋势,
结合统计图各自的特点,应选择折线统计图.
故选:B.
【点睛】本题主要考查统计图的选择,根据扇形统计图、折线统计图、条形统计图各自的特点来判断.
5.C
【分析】根据“各组数据个数之比为2:3:4:1”可求出第二小组的频数占30的,第三小组的频率为,计算得出答案.
【详解】解:因为各组数据个数之比为2:3:4:1,样本数据个数为30,
所以第二小组的频数为30×=9,
第三小组的频率为=0.4,
故选:C.
【点睛】本题考查了频率的计算方法,熟练掌握频率=频数÷总数是解答本题的关键.
6.A
【分析】根据频数分布直方图的组数的确定方法,用极差除以组距,然后根据组数比商的整数部分大1确定组数.
【详解】解:最大值为45,最小值为12,
极差为,
,
应分为7组.
故选A.
【点睛】本题考查频数分布直方图的组数的确定,解题的关键是注意组数比商的整数部分大1,不能四舍五入.
7.普查
【分析】根据抽样调查与普查的特点及被调查的事情的精度与难度,可行性等可得答案.
【详解】解:中国自行研制的全球卫星导航系统,对各部件的要求:必须百分百符合要求,
所以对我国最后一颗北斗卫星各零部件的调查,最适合采用的调查方式是普查.
故答案为:普查.
【点睛】本题考查的是抽样调查与普查的含义,掌握选择抽样调查与普查的依据是解题的关键.
8.20
【详解】试题分析:由“踢毽的扇形圆心角是60°,踢毽和打篮球的人数比是1:2”可得,踢毽的人数占总人数的比例以及打篮球的人数占的比例,由“各部分占总体的百分比之和为1”可得:参加“其它”活动的人数占总人数的比例.
解:由题意知,踢毽的人数占总人数的比例=60°÷360°=,
则打篮球的人数占的比例=×2=,
∴表示参加“其它”活动的人数占总人数的比例=1﹣﹣﹣30%=20%.
故答案为20%.
考点:扇形统计图.
9.27
【分析】根据统计图中的数据可以求得比赛总场数,从而可以求得足球队全年比赛胜的场数.
【详解】由统计图可得,
比赛场数为:10÷20%=50,
胜的场数为:50×(1﹣26%﹣20%)=50×54%=27,
故答案为27.
【点睛】主要考查条形统计图和扇形统计图,找出它们之间的关系式解题的关键.
10.8
【分析】观察统计图,得到最多的用水量和最少的用水量,求差即可.
【详解】根据图形可得:最多的用水量为36吨,最少的用水量为28吨.
36-28=8(吨)
故答案为:8
【点睛】本题考查从图形中读取信息,解题的关键在于准确找到最多的用水量和最少的用水量,
11.扇形统计图
【分析】根据扇形统计图和频数分布直方图的意义选择.
【详解】解:根据扇形统计图直接反映部分占总体的百分比大小,
可知学生成绩在60≤x<70之间的占一半以上,
所以能很好地说明一半以上国家的学生成绩在60≤x<70之间的是扇形统计图;
故答案为:扇形统计图.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
12.11
【分析】计算最大值与最小值的差,除以组距即可求得.
【详解】解:∵极差为:186-155=31,且组距为3,
则组数为31÷3≈11(组),
故答案为:11.
【点睛】此题考查的是组数的确定方法,掌握组数=极差÷组距是关键.
13.8
【分析】根据极差除以组距,取不小于该值的最小的整数即可得出组数.
【详解】解:∵次数最多为216,最少为62.若取组距为20,
∴,
故可以分成8组.
故答案为:8.
【点睛】本题考查了求频数分布组数,根据极差除以组距,取不小于该值的最小的整数得组数是解题的关键.
14.甲班
【分析】分别求出甲班与乙班成绩为D等级的人数进行比较即可.
【详解】解:由频数分布直方图知甲班成绩为D等级的人数为13人,
由扇形统计图知乙班成绩为D等级的人数为40×30%=12,
∴D等级较多的人数是甲班,
故答案为甲班.
【点睛】本题考查了频数分布直方图,扇形统计图,读懂统计图,从中找到必要的信息是解题的关键.
15.(1)50;5;10;
(2)见详解
(3)160
【分析】(1)根据频率=可求出n的值,进而求出a、b的值;
(2)根据(1)中的频数即可补全条形统计图;
(3)求出样本中,“喜欢太空抛物”的学生所占调查学生的百分比即可估计总体中的百分比,进而计算相应的人数.
【详解】(1)解:根据题意,;
;;
故答案为:50;5;10;
(2)解:补全条形图如下:
(3)解:该校最喜欢太空抛物实验的人数为:
(人);
【点睛】本题考查条形统计图、统计表以及样本估计总体,掌握频率=是解决问题的关键.
16.(1)200人
(2)108°
(3)1920人
【分析】(1)用B等级的人数除以B等级所占的百分比即可求解;
(2)用360度乘以C等级所占的百分比即可求解;
(3)用总人数乘以A和B等级所占的百分比即可.
【详解】(1)80÷40%=200(人)
答:本次抽样的学生人数为200人.
(2)360°×30%=108°,
答:扇形统计图中“C等级”所在扇形的圆心角是108°.
(3)(人),
答:估计该校学生对冬奥知识的了解程度为“A和B等级”的学生约有1920人.
【点睛】本题考查了条形统计图和扇形统计图,用样本估计总体,准确理解题意,熟练掌握知识点是解题的关键.
17.(1)500
(2)见解析
(3)480人
【分析】(1)根据类的人数是140,所占的比例是,即可求出总人数;
(2)根据(1)的结果即可求出的值,同理求得、两类的总人数,则的值即可求得,进而求得的值,进一步补全“阅读人数分组统计图”;
(3)直接利用样本估计总体计算即可.
(1)
解:总人数是:(人,
故答案为:500;
(2)
解:由题意,
、两类的人数的和是:(人,
则,
;
补全“阅读人数分组统计图”如下:
(3)
解:(人,
答:估计全校寒假课外阅读时间在20小时以下(不含20小时)的学生有480人.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;解题的关键是掌握利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
18.(1)
(2)
(3)
【分析】(1)先求出总人数,再利用扇形图中的数据分别求出b和c,最后求出a即可;
(2)把B中的百分比乘以即可求解;
(3)直接求出A和B的总人数占全体人数的百分比即可.
【详解】(1)总人数是:(人),
则,;
两类的人数之和是:,
则.
∴.
(2),
∴扇形统计图中的圆心角的度数是.
(3),
∴全校课外阅读时间在20小时以下(不含20小时)的学生大约占.
【点睛】本题考查了统计表和扇形统计图,解题关键是读懂题意,能从图表中获取相应信息进行求解.
19.(1)6,30;
(2)40,14;
(3)240人.
【分析】(1)分析图表即可知正确答案;
(2)利用A所占的频数为:6,频率为:0.15,可以求出样本容量,利用D所占的频率为:0.35,可以求出样本中认为最受启发的实验是D的学生人数;
(3)利用A、C、D各自所占的频数,求出B所占的频数,进一步估计出全校认为最受启发的实验是B的学生人数.
(1)
解:由图表可知:
认为最受启发的实验是A的学生人数为6人,认为最受启发的实验是C的学生人数占被调查学生总人数的百分比为30%;
(2)
解:∵A所占的频数为:6,频率为:0.15,
∴本次调查的样本容量为,
∵D所占的频率为:0.35,
∴样本中认为最受启发的实验是D的学生人数为(人);
(3)
解:∵A所占的频数为6,C所占的频数为:,D所占的频数为:14,
∴B所占的频数为:,
∴认为最受启发的实验是B的学生人数为:(人)
【点睛】本题考查频数,频率,样本容量,样本所占比求总体数量.比较简单,解题的关键是理解题意,结合图表进行分析计算.
20.(1)12,补全频数分布图见解析;(2)480只;(3)该村贫困户能脱贫.
【分析】(1)用总数量减去其它组的数量即为a的值;
(2)先求出随机抽取的50只中质量不小于的鸡占的比值,再乘以3000即可;
(3)先求出50只鸡的平均质量,根据市场价格,利润是15元/kg,再利用每千克利润×只数×每只的平均质量求出总利润,再进行比较即可.
【详解】(1)(只);
频数分布图如下:
故答案为:12;
(2)(只);
(3)(千克),
(元),
∵64800>54000,
∴该村贫困户能脱贫.
【点睛】本题考查由样本估计总体以及频数分布表和分布图,根据已知表格得出总体重与频数之间的关系是解题的关键.
21.(1)20,8,55
(2)补全直方图见解析,该市城区的空气质量等级为“中度污染”和“重度污染”的天数共27天
【分析】(1)用总天数乘以优的百分比即可得到m,总天数减去其他的天使即可得到n,用空气“良”的天数除以总天数再乘以百分百可得;
(2)根据m值补全图形,用365乘以空气质量等级为“中度污染”和“重度污染”的天数与80的比即可.
(1)
,
,
空气质量等级为“良”的天数占;
(2)
估计该市城区全年空气质量等级丙“中度污染”和“严重污染”的天数共(天),
补全统计图如图所示:
【点睛】本题考查的是直方图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.直方图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
一、单选题
1.(2022春·福建龙岩·七年级统考期末)下列调查中,适合用普查的是( )
A.新冠疫情期间检测地铁乘客的体温
B.调查全中国中学生的近视率
C.调查某品牌电视机的使用寿命
D.调查长江中现有鱼的种类
2.(2022春·福建厦门·七年级统考期末)为了了解某初中学校学生的视力情况,需要抽取部分学生进行调查.下列抽取学生的方法最合适的是( )
A.随机抽取该校一个班级的学生 B.随机抽取该校一个年级的学生
C.随机抽取该校一部分男生 D.分别从该校初一、初二、初三年级中各随机抽取10%的学生
3.(2022春·福建厦门·七年级统考期末)某校全体学生中随机抽取部分学生进行问卷调查,了解每周的劳动时间,按平均劳动时间t(单位:h)分为四组:A组“t<5”,B组“5≤t<7”,C组“7≤t<9”,D组“t>9”.将收集到的数据整理后,绘制成两幅不完整的统计图,如图所示.则下列说法错误的是( )
A.本次接受问卷调查的学生有100人
B.在扇形统计图中,B组占比为45%
C.在扇形统计图中,C组所占圆心角的度数为108°
D.该校共有1500名学生,估计该校平均每周劳动时间不少于7h的学生人数为675人
4.(2022春·福建福州·七年级统考期末)为了直观了解我国近十年人口增长率的变化趋势,最适合使用的统计图是( )
A.条形图 B.折线图 C.扇形图 D.频数分布直方图
5.(2022春·福建福州·七年级统考期末)已知样本数据个数为30,且被分成4组,各组数据个数之比为2:3:4:1,则第二小组频数和第三小组的频率分别为( )
A.0.4和0.3 B.0.4和9 C.9和0.4 D.12和9
6.(2022春·福建龙岩·七年级统考期末)有40个数据,其中最大值为45,最小值为12,若取组距为5,对数据进行分组,则应分为( )
A.7组 B.6组 C.5组 D.4组
二、填空题
7.(2022秋·福建漳州·七年级统考期末)中国北斗卫星导航系统是中国自行研制的全球卫星导航系统.是继美国全球定位系统()、俄罗斯格洛纳斯卫星导航系统()之后第三个成熟的卫星导航系统.在发射前,对我国最后一颗北斗卫星各零部件的调查,最适合采用的调查方式是__________.(填“普查”或“抽样调查”)
8.(2022春·福建福州·七年级统考期末)如图,整个圆表示某班参加课外活动的总人数,跳绳的人数占30%,表示踢毽的扇形圆心角是60°,踢毽和打篮球的人数比是12,那么表示参加“其它”活动的人数占总人数的____%.
9.(2022春·福建厦门·七年级统考期末)记录某足球队全年比赛结果(“胜”、“负”、“平”)的条形统计图和扇形统计图(不完整)如下:
根据图中信息,该足球队全年比赛胜了_____场.
10.(2022春·福建福州·七年级统考期末)某小区五月份1日至5日每天用水量变化情况如图所示,那么这天中用水量最多的一天比最少的一天多_______吨
11.(2022春·福建厦门·七年级统考期末)如图是2018年参加PISA测试(国际学生评估项目)的79个国家学生的数学平均成绩(x)的3个统计图,能最直观地说明一半以上国家的学生成绩在60≤x<70之间的统计图是 _____.(填“直方图”,“扇形统计图”,“折线统计图”)
12.(2022春·福建福州·七年级统考期末)体育老师从七年级学生中抽取40名参加全校的健身操比赛.这些学生身高(单位:)的最大值为186,最小值为155.若取组距为3,则可以分成__________组.
13.(2022春·福建莆田·七年级统考期末)某中学积极开展体育锻炼,一次跳绳活动后,七年一班体育委员统计了全班1分钟跳绳的次数,其中次数最多为216,最少为62.若取组距为20,则可以分成__________组.
14.(2022春·福建厦门·七年级统考期末)某中学九年级甲、乙两个班参加了一次数学考试,考试人数每班都为40人,每个班的考试成绩分为A、B、C、D、E五个等级,绘制的统计图如下:
根据以上统计图提供的信息,则D等级这一组人数较多的班是________
三、解答题
15.(2022春·福建莆田·七年级统考期末)2022年3月23日“天宫课堂”第二课在中国空间站正式开讲,“太空教师”翟志刚、王亚平、叶光富再次给大家带来一堂精彩的太空科普课.某校组织全校学生同步观看,直播结束后,教务处随机抽取了名学生,将他们最喜欢的太空实验分成四组,组:太空“冰雪”实验;B组:液桥演示实验;C组:水油分离实验;D组:太空抛物实验,并得到如下不完整的统计图表.请利用统计图表提供的信息回答下列问题:
学生最喜欢的太空实验人数统计表
分组 A组 B组 C组 D组
人数 a 15 20 b
(1)________,________,________;
(2)补全条形统计图;
(3)若全校同步观看直播的学生共有800人,请估计该校最喜欢太空抛物实验的人数.
16.(2022春·福建南平·七年级统考期末)2022年北京成功举办了第24届冬季奥林匹克运动会.为了调查同学们对冬奥知识的了解情况,某学校组织了“冬奥知识知多少”竞赛活动,随机抽取了部分学生的竞赛成绩进行分析,共分为四个等级:A,B,C,D,并绘制了如下不完整的统计图.请结合统计图表,回答下列问题:
(1)本次抽样的学生人数为多少人?
(2)扇形统计图中“C等级”所在扇形的圆心角是多少度?
(3)若该校共有学生3000人,请估计该校学生对冬奥知识了解情况的程度为“A和B等级”的学生约有多少人?
17.(2022春·福建厦门·七年级统考期末)某学校对学生寒假课外阅读时间进行抽样调查,将收集的数据分成A,B,C,D,E五组进行整理,并绘制成如下的统计图表(图中信息不完整).
阅读时间分组统计表
组别 阅读时间x(时) 人数
A a
B 100
C c
D 140
E e
请结合以上信息解答下列问题:
(1)本次共调查了 名学生;
(2)请补全“阅读人数分组统计图”;
(3)已知该校有2000名学生,估计全校寒假课外阅读时间在20小时以下(不含20小时)的学生有多少人?
18.(2022春·福建龙岩·七年级统考期末)某学校对学生的课外阅读时间进行抽样调查,将收集的数据五组进行整理,并绘制成如下所示的统计图表(图中信息不完整).
阅读时间分组统计表
组别 阅读时间x/时 人数
A a
B 100
C b
D 140
E c
请结合以上信息解答下列问题:
(1)求的值;
(2)求扇形统计图中B的圆心角的度数;
(3)估计全校课外阅读时间在20小时以下(不含20小时)的学生所占的比例.
19.(2022春·福建龙岩·七年级统考期末)022年3月23日下午,中国空间站“天宫课堂”再度开课,“太空教师”翟志刚、王亚平、叶光富演示了太空“冰雪”实验、液桥演示实验、水油分离实验、太空抛物实验.某校学生全员观看了太空授课直播,为了了解学生心中“最受启发的实验”的情况,随机抽取了部分学生(每人只选择一个实验)进行调查,以下是根据调查结果绘制的统计图表的一部分.
最受启发的实验 频数(人) 频率
A.“冰雪”实验 6 0.15
B.液桥演示实验
C.水油分离实验
D.太空抛物实验 0.35
根据以上信息,回答下列问题:
(1)被调查的学生中,认为最受启发的实验是A的学生人数为______人,认为最受启发的实验是C的学生人数占被调查学生总人数的百分比为______%;
(2)本次调查的样本容量为______,样本中认为最受启发的实验是D的学生人数为______人;
(3)若该校共有1200名学生,请根据调查结果,估计认为最受启发的实验是B的学生人数.
20.(2022春·福建厦门·七年级统考期末)2020年是脱贫攻坚年,为实现全员脱贫目标,某村贫困户在当地政府支持帮助下,办起了养鸡场,经过一段时间精心饲养,总量为3000只的一批鸡可以出售.现从中随机抽取50只,得到它们质量的统计数据如下:
质量 组中值 数量(只)
1.0 6
1.2 9
1.4 a
1.6 15
1.8 8
根据以上信息,解答下列问题:
(1)表中______,补全频数分布直方图;
(2)这批鸡中质量不小于的大约有多少只?
(3)这些贫困户的总收入达到54000元,就能实现全员脱贫目标.按15元的价格售出这批鸡后,该村贫困户能否脱贫?
21.(2022春·福建福州·七年级统考期末)某学校环保志者协会对该市城区的空气质量进行调查,从全年365天中随机抽取了80天的空气质量指数(AQI)数据,绘制出三幅不完整的统计图表.请根据图表中提供的信息解答下列问题:
AQI指数 质量等级 天数(天)
0-50 优
51-100 良 44
101-150 轻度污染
151-200 中度污染 4
201-300 重度污染 2
300以上 严重污染 2
(1)统计表中m=______,n=______.扇形统计图中,空气质量等级为“良”的天数占_____%;
(2)补全直方图,并通过计算估计该市城区的空气质量等级为“中度污染”和“重度污染”的天数共多少天?(结果保留整数)
参考答案:
1.A
【分析】根据全面调查和抽样调查的概念解答.
【详解】解:A、新冠疫情期间检测地铁乘客的体温,适合用普查;
B、调查全中国中学生的近视率,适合用抽查;
C、调查某品牌电视机的使用寿命,适合用抽查;
D、调查长江中现有鱼的种类,适合用抽查;
故选:A.
【点睛】本题考查的是全面调查和抽样调查,通过普查可以直接得到较为全面、可靠的信息,但花费的时间较长,耗费大,且一些调查项目并不适合普查.其一,调查者能力有限,不能进行普查.其二,调查过程带有破坏性.其三,有些被调查的对象无法进行普查.
2.D
【详解】因为要了解初中的视力情况范围较大、难度较大,所以应采取抽样调查的方法比较合适,本题考查的是调查方法的选择,正确选择调查方式要根据全面调查的优缺点再结合实际情况去分析,故只有D符合实际并具有普遍性,故选D.
3.D
【分析】根据C组的人数和所占的百分比求出调查的总人数,用B组的人数除以总人数求出B所占的百分比,用360°乘以C组所占的百分比,求出C组所占圆心角的度数,再用该校的总人数乘以该校平均每周劳动时间不少于7h的学生人数所占的百分比即可得出答案.
【详解】解:A、本次接受问卷调查的学生有30÷30%=100(人),故本选项正确,不符合题意;
B、在扇形统计图中,B组占比为×100%=45%,故本选项正确,不符合题意;
C、在扇形统计图中,C组所占圆心角的度数为:360°×=108°,故本选项正确,不符合题意;
D、该校共有1500名学生,估计该校平均每周劳动时间不少于7h的学生人数:1500×=600(人),故本选项错误,符合题意;
故选:D.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
4.B
【分析】由扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目,据此可得答案.
【详解】解:为了直观了解我国近十年人口增长率的变化趋势,
结合统计图各自的特点,应选择折线统计图.
故选:B.
【点睛】本题主要考查统计图的选择,根据扇形统计图、折线统计图、条形统计图各自的特点来判断.
5.C
【分析】根据“各组数据个数之比为2:3:4:1”可求出第二小组的频数占30的,第三小组的频率为,计算得出答案.
【详解】解:因为各组数据个数之比为2:3:4:1,样本数据个数为30,
所以第二小组的频数为30×=9,
第三小组的频率为=0.4,
故选:C.
【点睛】本题考查了频率的计算方法,熟练掌握频率=频数÷总数是解答本题的关键.
6.A
【分析】根据频数分布直方图的组数的确定方法,用极差除以组距,然后根据组数比商的整数部分大1确定组数.
【详解】解:最大值为45,最小值为12,
极差为,
,
应分为7组.
故选A.
【点睛】本题考查频数分布直方图的组数的确定,解题的关键是注意组数比商的整数部分大1,不能四舍五入.
7.普查
【分析】根据抽样调查与普查的特点及被调查的事情的精度与难度,可行性等可得答案.
【详解】解:中国自行研制的全球卫星导航系统,对各部件的要求:必须百分百符合要求,
所以对我国最后一颗北斗卫星各零部件的调查,最适合采用的调查方式是普查.
故答案为:普查.
【点睛】本题考查的是抽样调查与普查的含义,掌握选择抽样调查与普查的依据是解题的关键.
8.20
【详解】试题分析:由“踢毽的扇形圆心角是60°,踢毽和打篮球的人数比是1:2”可得,踢毽的人数占总人数的比例以及打篮球的人数占的比例,由“各部分占总体的百分比之和为1”可得:参加“其它”活动的人数占总人数的比例.
解:由题意知,踢毽的人数占总人数的比例=60°÷360°=,
则打篮球的人数占的比例=×2=,
∴表示参加“其它”活动的人数占总人数的比例=1﹣﹣﹣30%=20%.
故答案为20%.
考点:扇形统计图.
9.27
【分析】根据统计图中的数据可以求得比赛总场数,从而可以求得足球队全年比赛胜的场数.
【详解】由统计图可得,
比赛场数为:10÷20%=50,
胜的场数为:50×(1﹣26%﹣20%)=50×54%=27,
故答案为27.
【点睛】主要考查条形统计图和扇形统计图,找出它们之间的关系式解题的关键.
10.8
【分析】观察统计图,得到最多的用水量和最少的用水量,求差即可.
【详解】根据图形可得:最多的用水量为36吨,最少的用水量为28吨.
36-28=8(吨)
故答案为:8
【点睛】本题考查从图形中读取信息,解题的关键在于准确找到最多的用水量和最少的用水量,
11.扇形统计图
【分析】根据扇形统计图和频数分布直方图的意义选择.
【详解】解:根据扇形统计图直接反映部分占总体的百分比大小,
可知学生成绩在60≤x<70之间的占一半以上,
所以能很好地说明一半以上国家的学生成绩在60≤x<70之间的是扇形统计图;
故答案为:扇形统计图.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
12.11
【分析】计算最大值与最小值的差,除以组距即可求得.
【详解】解:∵极差为:186-155=31,且组距为3,
则组数为31÷3≈11(组),
故答案为:11.
【点睛】此题考查的是组数的确定方法,掌握组数=极差÷组距是关键.
13.8
【分析】根据极差除以组距,取不小于该值的最小的整数即可得出组数.
【详解】解:∵次数最多为216,最少为62.若取组距为20,
∴,
故可以分成8组.
故答案为:8.
【点睛】本题考查了求频数分布组数,根据极差除以组距,取不小于该值的最小的整数得组数是解题的关键.
14.甲班
【分析】分别求出甲班与乙班成绩为D等级的人数进行比较即可.
【详解】解:由频数分布直方图知甲班成绩为D等级的人数为13人,
由扇形统计图知乙班成绩为D等级的人数为40×30%=12,
∴D等级较多的人数是甲班,
故答案为甲班.
【点睛】本题考查了频数分布直方图,扇形统计图,读懂统计图,从中找到必要的信息是解题的关键.
15.(1)50;5;10;
(2)见详解
(3)160
【分析】(1)根据频率=可求出n的值,进而求出a、b的值;
(2)根据(1)中的频数即可补全条形统计图;
(3)求出样本中,“喜欢太空抛物”的学生所占调查学生的百分比即可估计总体中的百分比,进而计算相应的人数.
【详解】(1)解:根据题意,;
;;
故答案为:50;5;10;
(2)解:补全条形图如下:
(3)解:该校最喜欢太空抛物实验的人数为:
(人);
【点睛】本题考查条形统计图、统计表以及样本估计总体,掌握频率=是解决问题的关键.
16.(1)200人
(2)108°
(3)1920人
【分析】(1)用B等级的人数除以B等级所占的百分比即可求解;
(2)用360度乘以C等级所占的百分比即可求解;
(3)用总人数乘以A和B等级所占的百分比即可.
【详解】(1)80÷40%=200(人)
答:本次抽样的学生人数为200人.
(2)360°×30%=108°,
答:扇形统计图中“C等级”所在扇形的圆心角是108°.
(3)(人),
答:估计该校学生对冬奥知识的了解程度为“A和B等级”的学生约有1920人.
【点睛】本题考查了条形统计图和扇形统计图,用样本估计总体,准确理解题意,熟练掌握知识点是解题的关键.
17.(1)500
(2)见解析
(3)480人
【分析】(1)根据类的人数是140,所占的比例是,即可求出总人数;
(2)根据(1)的结果即可求出的值,同理求得、两类的总人数,则的值即可求得,进而求得的值,进一步补全“阅读人数分组统计图”;
(3)直接利用样本估计总体计算即可.
(1)
解:总人数是:(人,
故答案为:500;
(2)
解:由题意,
、两类的人数的和是:(人,
则,
;
补全“阅读人数分组统计图”如下:
(3)
解:(人,
答:估计全校寒假课外阅读时间在20小时以下(不含20小时)的学生有480人.
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;解题的关键是掌握利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
18.(1)
(2)
(3)
【分析】(1)先求出总人数,再利用扇形图中的数据分别求出b和c,最后求出a即可;
(2)把B中的百分比乘以即可求解;
(3)直接求出A和B的总人数占全体人数的百分比即可.
【详解】(1)总人数是:(人),
则,;
两类的人数之和是:,
则.
∴.
(2),
∴扇形统计图中的圆心角的度数是.
(3),
∴全校课外阅读时间在20小时以下(不含20小时)的学生大约占.
【点睛】本题考查了统计表和扇形统计图,解题关键是读懂题意,能从图表中获取相应信息进行求解.
19.(1)6,30;
(2)40,14;
(3)240人.
【分析】(1)分析图表即可知正确答案;
(2)利用A所占的频数为:6,频率为:0.15,可以求出样本容量,利用D所占的频率为:0.35,可以求出样本中认为最受启发的实验是D的学生人数;
(3)利用A、C、D各自所占的频数,求出B所占的频数,进一步估计出全校认为最受启发的实验是B的学生人数.
(1)
解:由图表可知:
认为最受启发的实验是A的学生人数为6人,认为最受启发的实验是C的学生人数占被调查学生总人数的百分比为30%;
(2)
解:∵A所占的频数为:6,频率为:0.15,
∴本次调查的样本容量为,
∵D所占的频率为:0.35,
∴样本中认为最受启发的实验是D的学生人数为(人);
(3)
解:∵A所占的频数为6,C所占的频数为:,D所占的频数为:14,
∴B所占的频数为:,
∴认为最受启发的实验是B的学生人数为:(人)
【点睛】本题考查频数,频率,样本容量,样本所占比求总体数量.比较简单,解题的关键是理解题意,结合图表进行分析计算.
20.(1)12,补全频数分布图见解析;(2)480只;(3)该村贫困户能脱贫.
【分析】(1)用总数量减去其它组的数量即为a的值;
(2)先求出随机抽取的50只中质量不小于的鸡占的比值,再乘以3000即可;
(3)先求出50只鸡的平均质量,根据市场价格,利润是15元/kg,再利用每千克利润×只数×每只的平均质量求出总利润,再进行比较即可.
【详解】(1)(只);
频数分布图如下:
故答案为:12;
(2)(只);
(3)(千克),
(元),
∵64800>54000,
∴该村贫困户能脱贫.
【点睛】本题考查由样本估计总体以及频数分布表和分布图,根据已知表格得出总体重与频数之间的关系是解题的关键.
21.(1)20,8,55
(2)补全直方图见解析,该市城区的空气质量等级为“中度污染”和“重度污染”的天数共27天
【分析】(1)用总天数乘以优的百分比即可得到m,总天数减去其他的天使即可得到n,用空气“良”的天数除以总天数再乘以百分百可得;
(2)根据m值补全图形,用365乘以空气质量等级为“中度污染”和“重度污染”的天数与80的比即可.
(1)
,
,
空气质量等级为“良”的天数占;
(2)
估计该市城区全年空气质量等级丙“中度污染”和“严重污染”的天数共(天),
补全统计图如图所示:
【点睛】本题考查的是直方图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.直方图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
