有理数的乘法(1)[上学期]
文档属性
| 名称 | 有理数的乘法(1)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 153.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-09-24 08:09:00 | ||
图片预览


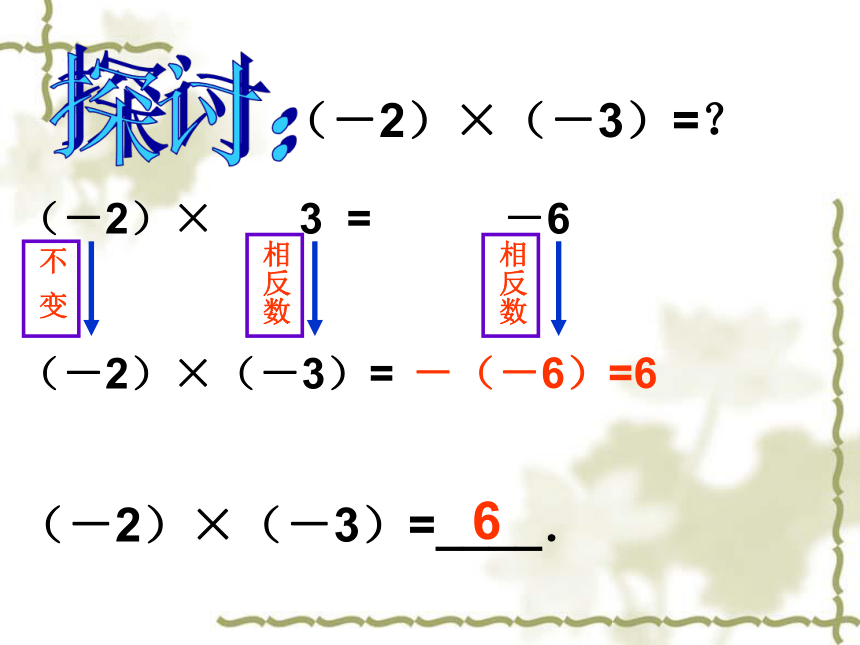

文档简介
课件13张PPT。有理数的乘法算一算⑴ 2× ⑵ 0 ×7.5
⑶ 1×56 ⑷ 2×3
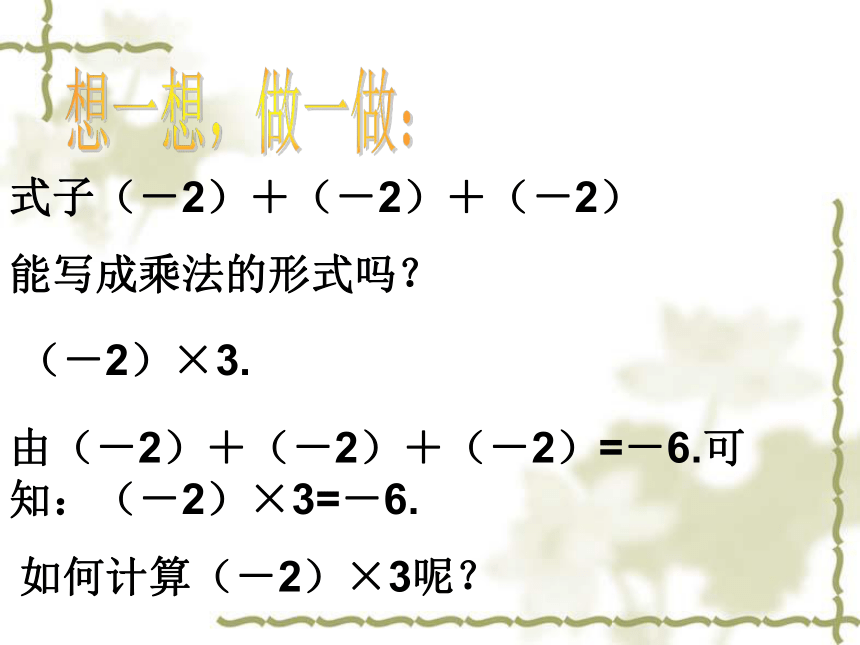
⑸ (-2)+(-2)+(-2)=-6式子(-2)+(-2)+(-2)
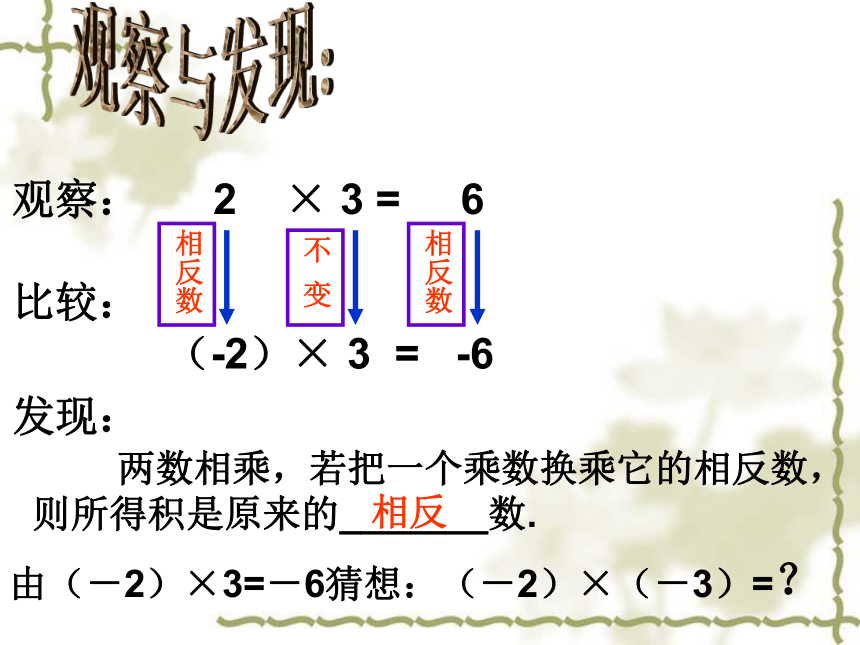
能写成乘法的形式吗?想一想,做一做:(-2)×3.如何计算(-2)×3呢?由(-2)+(-2)+(-2)=-6.可知:(-2)×3=-6.观察与发现:观察: 2 × 3 = 6
比较:
(-2)× 3 = -6相反数相反数不 变发现:由(-2)×3=-6猜想:(-2)×(-3)=? 两数相乘,若把一个乘数换乘它的相反数,则所得积是原来的_______数.相反(-2)× 3 = -6
(-2)×(-3)=-(-6)=6 探讨:(-2)×(-3)=?不 变相反数相反数(-2)×(-3)=____.6积的符号与两乘数符号的关系:正数乘正数积为————————数,负数乘正数积为————————数,正数乘负数积为————————数,负数乘负数积为————————数。积的绝对值与两乘数绝对值的关系:乘积的绝对值等于各乘数绝对值的_______。正正负负乘积思考:任意数与0相乘,得数是多少?例 题 解 析例1 计算:
(1) (?4)×5 (2) (?4)×(?7)
(3) (4)解:(1) (?4)×5 (2) (?4)×(?7)
= ?(4×5) =+(4×7)
=?20 =28(3) (4)=1=1 求解中的第一步是 ;确定积的符号 第二步
是 。绝对值相乘看谁做得又对又快:⑴6×(-9); ⑵(-4)×6;
⑶(-6)×(-1);⑷(-6)×9;
⑸ × ; ⑹ × .倒 数 的 定 义 由例 1 的 (3) 、(4)的求解:? 解题后的反思 ? (3) (4)=1=1可知 我们把乘积为 1 的两个有理数称为互为倒数.1.写出下列各数的倒数:
1,-1, , ,5, -5, , .动手又动脑2.观察并讨论:
⑴0有没有倒数?
⑵一个数的倒数等于它的本身,那么这个数是_____.
⑶如果两数互为相反数(0除外),那么它们的倒数也是互为相反数吗? 用正负数表示气温的变化量,上升为正,下降为负,
登山队攀登一座山峰,每登高1km,气温的变化量为
-60C,向上攀登3km后,气温有什么变化? 继续向上攀
登-3km之后 ,气温又如何变化?此时登山队位于何处?
hkm(h+3)km解:(1) (- 6) ×3= - 18答:气温下降180C。(2)(-6)×(-3)=18答:气温上升180C ,此时
登山队回到原出发点。例二:1.本节课你最大的收获是什么?
2.有理数的乘法与小学的(正数)的乘法有什么联系和不同点?
小结 思考 GOODBYE!
⑶ 1×56 ⑷ 2×3
⑸ (-2)+(-2)+(-2)=-6式子(-2)+(-2)+(-2)
能写成乘法的形式吗?想一想,做一做:(-2)×3.如何计算(-2)×3呢?由(-2)+(-2)+(-2)=-6.可知:(-2)×3=-6.观察与发现:观察: 2 × 3 = 6
比较:
(-2)× 3 = -6相反数相反数不 变发现:由(-2)×3=-6猜想:(-2)×(-3)=? 两数相乘,若把一个乘数换乘它的相反数,则所得积是原来的_______数.相反(-2)× 3 = -6
(-2)×(-3)=-(-6)=6 探讨:(-2)×(-3)=?不 变相反数相反数(-2)×(-3)=____.6积的符号与两乘数符号的关系:正数乘正数积为————————数,负数乘正数积为————————数,正数乘负数积为————————数,负数乘负数积为————————数。积的绝对值与两乘数绝对值的关系:乘积的绝对值等于各乘数绝对值的_______。正正负负乘积思考:任意数与0相乘,得数是多少?例 题 解 析例1 计算:
(1) (?4)×5 (2) (?4)×(?7)
(3) (4)解:(1) (?4)×5 (2) (?4)×(?7)
= ?(4×5) =+(4×7)
=?20 =28(3) (4)=1=1 求解中的第一步是 ;确定积的符号 第二步
是 。绝对值相乘看谁做得又对又快:⑴6×(-9); ⑵(-4)×6;
⑶(-6)×(-1);⑷(-6)×9;
⑸ × ; ⑹ × .倒 数 的 定 义 由例 1 的 (3) 、(4)的求解:? 解题后的反思 ? (3) (4)=1=1可知 我们把乘积为 1 的两个有理数称为互为倒数.1.写出下列各数的倒数:
1,-1, , ,5, -5, , .动手又动脑2.观察并讨论:
⑴0有没有倒数?
⑵一个数的倒数等于它的本身,那么这个数是_____.
⑶如果两数互为相反数(0除外),那么它们的倒数也是互为相反数吗? 用正负数表示气温的变化量,上升为正,下降为负,
登山队攀登一座山峰,每登高1km,气温的变化量为
-60C,向上攀登3km后,气温有什么变化? 继续向上攀
登-3km之后 ,气温又如何变化?此时登山队位于何处?
hkm(h+3)km解:(1) (- 6) ×3= - 18答:气温下降180C。(2)(-6)×(-3)=18答:气温上升180C ,此时
登山队回到原出发点。例二:1.本节课你最大的收获是什么?
2.有理数的乘法与小学的(正数)的乘法有什么联系和不同点?
小结 思考 GOODBYE!
