高中物理人教版(2019)必修第二册同步课件:6.4 生活中的圆周运动(90张PPT)
文档属性
| 名称 | 高中物理人教版(2019)必修第二册同步课件:6.4 生活中的圆周运动(90张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 46.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-16 13:34:51 | ||
图片预览









文档简介
(共90张PPT)
第六章 圆周运动
6.4 生活中的圆周运动
人教版(2019)
2022-2023学年高中物理同步备课必修第二册
目录
contents
火车转弯
01
02
汽车过拱形桥
03
航天器中的失重现象
04
离心运动
物体做圆周运动时需要什么力?谁来提供?
向心力,合力提供
向心力的特点?
方向:
大小:
时刻指向圆心
物体做匀速圆周运动时,所受合外力有何特点?
合外力全部提供向心力,合外力的大小不变,方向始终指向圆心
知识回顾
提供物体做圆周运动的力
做圆周运动的物体所需的力
从“供” “需”两方面研究生活中做圆周运动的物体
由物体受力情况决定
由物体的运动情况决定
=
“供需”平衡 物体做匀速圆周运动
本节课
牛顿第二定律F=ma的应用
向心力公式深化理解
导入新课
在铁路弯道处,稍微留意一下,就能发现内、外轨道的高度略有不同。你能解释其中的原因吗
内侧轨道
外侧轨道
水平线
假设内、外轨道的倾斜程度与水平线之间的角度为。
火车转弯时的轨迹可以视为一段小圆弧,故我们可以将火车的转弯视为很小的一段圆周运动。
火车转弯时的轨迹可以视为一段小圆弧,故我们可以将火车的转弯视为很小的一段圆周运动,满足圆周运动的规律,可以用圆周运动的方法分析。
转弯的轨迹
火车转弯是什么力提供向心力?
想一想
火车转弯
01
铁轨
踏面
轮缘
车轮的构造
铁轨模型
结论
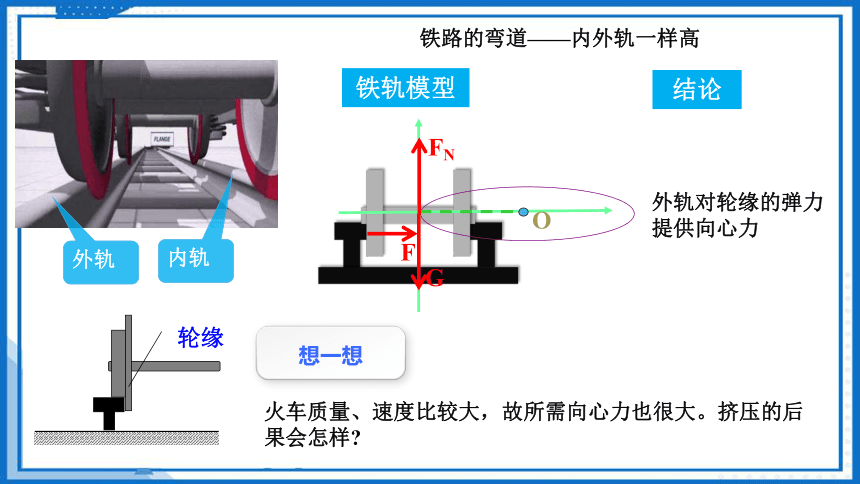
外轨
内轨
外轨对轮缘的弹力提供向心力
铁路的弯道——内外轨一样高
火车质量、速度比较大,故所需向心力也很大。挤压的后果会怎样
O
F
G
FN
轮缘
想一想
FN
F
G
内外轨道一样高时转弯
火车车轮受三个力:重力、支持力、外轨对轮缘的弹力.
外轨对轮缘的弹力F提供向心力F=F向
由于该弹力是由轮缘和外轨的挤压产生的,且由于火车质量很大,故轮缘和外轨间的相互作用力很大,易损坏铁轨.
怎么办
请同学们仔细观看视频,观察真实的火车轨道是怎样的?
铁路的弯道——外轨高于内轨
铁路的弯道
θ
FN
在转弯处外轨略高于内轨
火车转弯所需的向心力的方向是在水平方向上还是在与斜面平行的方向上?
G
O
F合
θ
O
G
FN
F合
θ
θ
F合=mg tanθ
轨道对轮缘无挤压,此时火车的速度为多大?
火车转弯时所需的向心力
Fn = m
v2
R
v= gR tanθ
若火车的速度大于或小于这个值时,轨道对轮缘有挤压吗?
2、当 v< gR tanθ :
1、当 v> gR tanθ :
G
FN
θ
轮缘受到外轨向内的弹力
G
FN
θ
F
F
轮缘受到内轨向外的弹力
想一想
若火车的速度大于或小于这个值时,会怎么样呢?
G
Fn
N
h
L
θ
θ
R
此为火车转弯时的安全速度
h、R越大,火车转弯越安全
θ很小时,sinθ=tanθ
此时轮缘与铁轨无弹力作用
(1)、当火车行驶速率 时,Fn=F合,内外轨道都不受挤压,对两轮缘都没有压力
(3)、当火车行驶速率 时, Fn=F合-F侧,内轨道受到挤压对轮缘有侧压力
(2)、当火车行驶速率 时,Fn=F合+F侧,外轨道受到挤压对轮缘有侧压力
在实际生活中,铁路修好后θ(h、L)、r是确定的,所以火车转弯的安全速度也为定值
F合=mg tanθ
总 结
西班牙超速列车脱轨事件
O
mg
FN
f
汽车在水平地面上转弯是什么力提供向心力的呢
汽车转弯
想一想
汽车在水平地面上转弯是什么力提供向心力的呢
O
mg
FN
Ff
汽车在水平路面上转弯所需要的向心力来源:汽车侧向所受的静摩擦力。
O
mg
FN
Ff
当汽车转弯的半径一定时,汽车的速度v越大,所需的向心力也越大,静摩擦力也越大,当静摩擦力为最大静摩擦力时:
O
mg
FN
Ff
由此可见:当汽车转弯时,存在一个安全通过的最大速度,如果超过了这个速度,汽车将发生侧滑现象。
改进措施:
(1)增大转弯半径
(2)增加路面的粗糙程度
(3)最重要的一点:司机应该减速慢行!
(4)增加路面高度差——外高内低
汽车转弯时的措施:
把转弯处的道路修成外高内低。(高速路和赛道)
G
FN
F向
观察下面两幅图片,赛道及告诉公路弯道有什么特点?为什么要这样设计?
路面是倾斜的
外高内低
赛道的设计
N
Fn
mg
思考与赛道类似的例题
例:球沿光滑圆锥内壁在水平面内做匀速圆周运动,如图。试分析向心力的来源。(圆锥摆模型)
N
G
θ
将路面倾斜的原因是让支持力与竖直方向成一角度,这样支持力的水平分力就可以提供部分向心力,减小静摩擦力的负担。
讨论:如果倾斜路面是光滑的,汽车还能转弯吗?
如果能,对速度有什么要求?
结 论
问题:如果倾斜路面是光滑的,汽车还能转弯吗?
如果能,对速度有什么要求?
能,根据上面例题可知,即使没有摩擦力,只靠重力与支持力的合力充当向心力也可以做圆周运动,此时的速度是个定值,假设路面与水平面夹角为θ,则有
问题:如果汽车转弯速度大于这个值呢?或者小于这个值呢?
如果大于这个值,则汽车向上滑,如果小于这个值,则向下滑。
飞机转弯:类似于火车转弯
G
F
Fn
例1、火车以半径R= 900 m转弯,火车质量为8×105kg ,速度为30m/s,火车轨距l=1.4 m,要使火车通过弯道时仅受重力与轨道的支持力,轨道应该垫的高度h?(θ较小时tanθ=sinθ)
FN
mg
F
θ
h
由力的关系得:
由向心力公式得:
由几何关系得:
解:
=0.14m
例2 . 有一列重为100 t的火车,以72 km/h的速率匀速通过一个内外轨一样高的弯道,轨道半径为400 m.(g取10 m/s2)
(1)试计算铁轨受到的侧压力;
(2)若要使火车以此速率通过弯道,且使铁轨受到的侧压力为零,我们可以适当倾斜路基,试计算路基倾斜角度θ的正切值.
FN
mg
汽车过拱形桥
02
拱形桥
(凸形桥)
凹形桥
水平桥
生活中为什么我们经常见到凸桥,很少见到凹桥,相比之下凸桥有哪些优点呢?
凸桥可以让更大的船只通过,利于通航。
发洪水的时候,凸桥在相同的时间内可以流过更多的水,利于泄洪。
更加坚固、美观……
黄石长江大桥
泸定桥
问题1:汽车静止在桥上与通过平桥时,受力怎样?
F压=FN=mg
思考与讨论
问题2:汽车过拱形桥时,在最高点时,车对凸桥的压力又怎样?
mg
FN
v2
R
mg-FN=m
v2
R
FN =mg-m
v2
R
F压=FN =mg-m
汽车对桥的压力小于其所受重力,即处于失重
FN <mg
思考与讨论
v2
R
mg=m
当 FN = 0 时,汽车脱离桥面,做平抛运动,汽车及其中的物体处于完全失重状态。
FN=0 时,汽车的速度为多大?
v2
R
FN =mg-m
问题3:汽车过拱形桥时,运动速度变大,车对凸桥的压力如何变化?
mg
FN
临界速度
思考与讨论
总结:重力及支持力沿半径方向的合力提供向心力。若汽车的速度过大,将会离开桥面做斜抛运动。
若汽车即将离开桥面时,则有FN =0,故
若汽车不在拱形桥的最高点或最低点时,如何分析汽车的运动情况呢?
θ
v2
R
mgcosθ-FN =m
v2
R
FN =mgcosθ-m
v2
R
F压=FN =mgcosθ -m
FN <mg (失重)
v= gR cosθ
可知:桥面所受的压力与夹角θ、车速v都有关;
故汽车过凸形桥时,汽车对桥的压力总小于重力。
问题4:汽车过凹形桥时,在最低点时,车对凹形桥的压力又怎样?
FN
mg
v2
R
FN =mg + m
v2
R
F压=FN =mg + m
v2
R
FN-mg=m
汽车对桥的压力大于其所受重力,即处于超重
若汽车通过凹桥的速度增大,会出现什么情况?
FN >mg
思考与讨论
F压=FN <mg
失重
超重
F压=FN =mg
F压=FN >mg
比较三种桥面受力的情况
凸形桥
泸定桥
过水路面
凹形桥
例1.一辆卡车在丘陵地匀速行驶,地形如图所示,由于轮胎太旧,途中爆胎,爆胎可能性最大的地段应是( )
A. a处 B. b处 C. c处 D. d处
a
b
c
d
D
例2、一辆汽车匀速率通过半径为R的圆弧拱形路面,关于汽车的受力情况,下列说法正确的是( )
A、汽车对路面的压力大小不变,总是等于汽车的重力
B、汽车对路面的压力大小不断发生变化,总是小于汽车所受重力
C、汽车的牵引力不发生变化
D、汽车的牵引力逐渐变小
BD
例3. 一辆质量 m =2 t 的轿车,驶过半径 R = 50 m 的一段凸形桥面,g 取 10 m/s2,求:
(1) 轿车以 10 m/s 的速度通过桥面最高点时,对桥面的压力是多大
(2) 在最高点对桥面的压力等于轿车重力的一半时,车的速度大小是多少
16000 N
航天器中的失重现象
03
地球可以看做一个巨大的拱形桥,桥面的半径就是地球的半径.会不会出现这样的情况:速度大到一定程度时,地面对车的支持力是零?这时驾驶员与座椅之间的压力是多少?……
mg
思考与讨论
地球可以看作一个巨大的拱型桥,其半径就是地球半径R= 6400km,若汽车不断加速,则地面对它的支持力就会变小,汽车速度多大时,支持力会变成零FN=0?
此时司机处于完全失重状态。
由
得
想一想
生活实例:航天器中的失重现象
汽车车速为v,地球半径为R
汽车对桥面的压力为0
G=9.8N/kg,R=6371km
v ≈7900m/s
1、航天器在发射升空(加速上升)时,航天员处在超重还是失重状态?
2、航天器在轨道正常运行(绕地球做匀速圆周运动)时,航天员处在超重还是失重状态?
超重
FN
mg
a
FN-mg =ma
FN>mg
想一想
v2
r
FN =mg-m
航天器绕地球做匀速圆周运动,假设它的线速度的大小为v ,轨道半径近似等于地球半径R ,航天员受到的地球引力近似等于他在地面测得的体重mg .
v= gR
当 时,座舱对航天员的支持力FN=0 ,航天员处于完全失重.
有人把航天器失重的原因说成是它离地球太远,从而摆脱了地球引力,这种说法对吗?
正是由于地球引力的存在,才使航天器连同其中的人和物体绕地球做圆周运动.
v2
R
mg-FN=m
FN <mg
失重
想一想:什么维持近地航天器做圆周运动?
万有引力
有人把航天器失重的原因说成是它离地球太远,从而摆脱了地球引力,这种说法对吗?
正是由于地球引力的存在,才使航天器连同其中的人和物体绕地球做圆周运动.
如果地球的引力突然消失,航天器将做什么样的运动呢?
想一想
离心运动
04
O
F合 = mω2r,
F合<mω2r ,
F 合= 0 ,
1、定义:做匀速圆周运动的物体,在所受合力突然消失,或者不足以提供圆周运动所需的向心力时,做逐渐远离圆心的运动,这种运动叫做离心运动.
2、条件:
0 ≤F合<mω2r
供<需
物体沿切线方向飞出远离圆心
物体做匀速圆周运动
物体做逐渐远离圆心的运动
(1) 当 F=mω2r 时,物体做匀速圆周运动;
(2) 当 F=0 时,物体沿切线方向飞出;
(3) 当 F<mω2r 时,物体逐渐远离圆心;
(4) 当 F>mω2r 时,物体逐渐靠近圆心。
理解:
(1)物体做离心运动,并不是受到“离心力”作用,更不是“离心力”大于向心力,而是外界提供的向心力不足或突然消失。
(2)离心运动不是沿着半径背离圆心的运动,而是沿着切线或曲线离心的运动。
结 论
离心运动的应用
离心抛掷
离心甩干
离心脱水
离心分离
(1)离心运动的应用
①甩干雨伞上的水滴
②链球运动
在田径比赛中,链球项目就是得用离心现象来实现投掷的。链球的投掷是通过预摆和旋转来完成的,运动员手持链球链条的一端,在链球高速旋转时,突然松手,拉力消失,链就沿切线方向飞出去。
在雨天,我们可以通过旋转雨伞
的方法甩干雨伞上的水滴,旋转时,当转动快到一定的程度时,水滴和雨伞之间的附着力满足不了水滴做圆周运动所需的向心力,水滴就会做远离圆心的运动而被甩出去。
把湿布块放在离心干燥器的金属网笼里,网笼转得比较慢时,水滴跟物体的附着力 F足以提供所需要的向心力,使水滴做圆周运动,当网笼转的比较快时,附着力 F 不足以提供所需要的向心力,于是水滴做离心运动,穿过网孔,飞到网笼外面。洗衣机的脱水筒也是利用离心运动把湿衣服甩干的。
③离心干燥器
o
FF
v
、制作“棉花”糖的原理:
内筒与洗衣机的脱水筒相似,往内筒加入白砂糖,加热使糖熔化成糖汁,内筒高速旋转,黏稠的糖汁就做离心运动,从内筒壁的小孔飞散出去,成为丝状,到达温度较低的外筒就会迅速冷却凝固,变得纤细雪白,像一团团棉花。
“离心浇铸”技术
模具绕一固定轴旋转,当达到500转每分时,将融化了的液态金属倒入其中,它将以巨大的惯性离心力向模具壁紧压,同时夹杂在液态金属里的气体和熔渣,由于其密度远小于液态的金属,因此它们将从金属里被分离出来。按此法浇铸出的金属零件密实、均匀、不含气泡和裂痕,大大提高了使用寿命。
啤酒何以清澈透亮?
原来这也与离心分离密切相关。因为麦汁中含有一种极不稳定的冷凝固物,应尽量减少其含量才能保证啤酒不出现冷混浊现象。然而,这种冷凝固物的粒子极为微小,直径仅有0.1―0.5微米,很难除净。但若采用高速离心机进行分离处理,就比较容易实现净化。因为这种粒子虽然微小,但由于存在密度差,一旦进入强大的离心力场后,二者立即“分道扬镳”,从而可以很容易地把冷凝固粒子剔除。
从蔗糖水溶液中分离蔗糖,也需依靠离心沉降方法 。
当离心机转得比较慢时,缩口的阻力 F 足以提供所需的向心力,缩口上方的水银柱做圆周运动。 当离心机转得相当快时,阻力 F 不足以提供所需的向心力,水银柱做离心运动而进入玻璃泡内。
离心沉淀器
要使原来作匀速圆周运动的物体作离心运动,该怎么办?
1、提高转速,使所需向心力增大到大于物体所受合外力.
2、减小合外力或使其消失.
供=需
供<需
想一想
赛道设计
离心运动的危害与防止
交通限速
O
F静
v
在水平公路上行驶的汽车,转弯时所需的向心力是由车轮与路面的静摩擦力提供的。如果转弯时速度过大,所需向心力Fn大于最大静摩擦力Fmax (Fmax不足以提供向心力),汽车将做离心运动而造成交通事故.因此,在公路弯道处,车辆行驶不允许超过规定的速度.
当 时,汽车做离心运动
Fmax<m
v2
r
离心运动的防止
高速转动的砂轮、飞轮等,都不得超过允许的最大转速。转速过高时,砂轮、飞轮内部分子间的相互作用力不足以提供所需向心力,离心运动会使它们破裂,酿成事故.
O
F
v
为什么转动的砂轮、飞轮等都要限速?
要防止离心现象发生,该怎么办?
1、减小物体运动的速度,使物体作圆周运动时所需的向心力减小.
2、增大合外力,使其达到物体作圆周运动时所需的向心力.
供<需
供=需
想一想
摩托车飞车走壁,请分析受力情况,解释现象
1. 如图所示,光滑水平面上,质量为 m 的小球在拉力 F 作用下做匀速圆周运动。若小球运动到 P 点时,拉力 F 发生变化,下列关于小球运动情况的说法中正确的是( )
BC
若拉力突然变大,小球将沿轨迹
Pb 做离心运动
B. 若拉力突然变小,小球将沿轨迹
Pb 做离心运动
C. 若拉力突然消失,小球将沿轨迹
Pa 做离心运动
D. 若拉力突然变小,小球将沿轨迹
Pc 做近心运动
2. 如图所示,光滑圆盘中心有一个小孔,用细绳穿过小孔,两端各系一小球 A、B,A、B 等质量,盘上的小球 A 做半径为 r = 20 cm 的匀速圆周运动,若要保持 B 球静止,A 球的角速度多大?
A
B
F
F
解:对于 A,根据牛顿第二定律
F = mω2r
对于 B,F = mg
解得
3.下列有关洗衣机脱水筒的脱水原理说法正确的是 ( )
A.水滴受离心力作用,而沿背离圆心的方向甩出
B.水滴受到向心力,由于惯性沿切线方向甩出
C.水滴受到的离心力大于它受到的向心力,从而沿切线方向甩出
D.水滴与衣服间的附着力小于它所需的向心力,于是沿切线方向甩出
D
4.人造地球卫星绕地球做匀速圆周运动,下列说法中正确的有 ( )
A.可以用天平测量物体的质量
B.可以用水银气压计测舱内的气压
C.可以用弹簧测力计测拉力
D.在卫星内将重物挂于弹簧测力计上,弹簧测力计示数为零,但重物仍受地球的引力
CD
课堂小结
火车转弯
汽车过桥
失重现象
离心运动
当 v< gR tanθ :
当 v> gR tanθ :轮缘受到外轨向内的弹力
轮缘受到内轨向外的弹力
FNFN>mg:超重
做离心运动的条件:
典例分析
05
【练习1】(2022秋·重庆市育才中学高一期末)(多选)在修筑铁路时,弯道处的外轨会略高于内轨。如图所示,当火车以规定的行驶速度转弯时,内、外轨均不会受到轮缘的挤压,设此时的速度大小为v,重力加速度为g,两轨所在面的倾角为θ,则( )
A.该弯道的半径
B.当火车质量改变时,规定的行驶速度大小不变
C.当火车速率大于v时,内轨将受到轮缘的挤压
D.当火车速率小于v时,外轨将受到轮缘的挤压
【参考答案】AB
【练习2】汽车在过凹凸路面时,都会做减速操作,如图A、B分别是一段凹凸路面的最高点和最低点,若把汽车视作质点,则下列说法正确的是( )
A.汽车行驶到A点时,处于超重状态,如果采取加速操作会使车胎受到更大的压力
B.汽车行驶到B点时,处于超重状态,如果采取加速操作会使汽车飞离路面
C.汽车行驶到A点时,处于失重状态,如果采取减速操作会增加车胎与路面间的弹力,使得行驶更加稳定安全
D.汽车行驶到B点时,处于失重状态,如果采取减速操作会增加车胎与路面间的弹力,使得行驶更加稳定安全
【参考答案】C
【练习3】翻滚过山车是一种非常刺激而有趣的游乐项目。如图甲所示,小刚同学所坐的翻滚过山车正在下行中,如图乙所示,他此时所做的运动及所受合力的可能方向分别是( )
A.匀速圆周运动、沿F1方向
B.匀速圆周运动、沿F2方向
C.加速圆周运动、沿F3方向
D.减速圆周运动、沿F2方向
【参考答案】C
【练习4】(2023秋·长春外国语高一期末)(多选)若将短道速滑运动员在弯道转弯的过程看成在水平冰面上的一段匀速圆周运动,转弯时冰刀嵌入冰内从而使冰刀受与冰面夹角为θ(蹬冰角)的支持力,不计一切摩擦,弯道半径为R,重力加速度为g。以下说法正确的是( )
A.地面对运动员的作用力与重力与重力大小相等
B.武大靖转弯时速度的大小为
C.若武大靖转弯速度变大则需要减小蹬冰角
D.武大靖做匀速圆周运动,他所受合外力保持不变
【参考答案】BC
【练习5】气嘴灯安装在自行车的气嘴上,骑行速度在一定范围内会发光。一种气嘴灯的感应装置结构如图所示,一重物套在光滑杆上,并与弹簧连接,重物上的触点M与固定在B端的触点N接触后,LED灯就会发光。则下列说法正确的是( )
A.气嘴灯运动至最低点时处于失重状态
B.当车速较小时,重物的重力大于弹簧的弹力,使得触点MN接触,LED灯发光
C.当车速较大时,重物受到的合力不足以提供所需向心力,重物做离心运动,使得触点MN接触,LED灯发光
D.气嘴灯做圆周运动时,重物
受到重力、弹力和向心力的作用
【参考答案】C
感谢您的耐心聆听
I'd like to finish by saying how grateful I am for your attention.
第六章 圆周运动
6.4 生活中的圆周运动
人教版(2019)
2022-2023学年高中物理同步备课必修第二册
目录
contents
火车转弯
01
02
汽车过拱形桥
03
航天器中的失重现象
04
离心运动
物体做圆周运动时需要什么力?谁来提供?
向心力,合力提供
向心力的特点?
方向:
大小:
时刻指向圆心
物体做匀速圆周运动时,所受合外力有何特点?
合外力全部提供向心力,合外力的大小不变,方向始终指向圆心
知识回顾
提供物体做圆周运动的力
做圆周运动的物体所需的力
从“供” “需”两方面研究生活中做圆周运动的物体
由物体受力情况决定
由物体的运动情况决定
=
“供需”平衡 物体做匀速圆周运动
本节课
牛顿第二定律F=ma的应用
向心力公式深化理解
导入新课
在铁路弯道处,稍微留意一下,就能发现内、外轨道的高度略有不同。你能解释其中的原因吗
内侧轨道
外侧轨道
水平线
假设内、外轨道的倾斜程度与水平线之间的角度为。
火车转弯时的轨迹可以视为一段小圆弧,故我们可以将火车的转弯视为很小的一段圆周运动。
火车转弯时的轨迹可以视为一段小圆弧,故我们可以将火车的转弯视为很小的一段圆周运动,满足圆周运动的规律,可以用圆周运动的方法分析。
转弯的轨迹
火车转弯是什么力提供向心力?
想一想
火车转弯
01
铁轨
踏面
轮缘
车轮的构造
铁轨模型
结论
外轨
内轨
外轨对轮缘的弹力提供向心力
铁路的弯道——内外轨一样高
火车质量、速度比较大,故所需向心力也很大。挤压的后果会怎样
O
F
G
FN
轮缘
想一想
FN
F
G
内外轨道一样高时转弯
火车车轮受三个力:重力、支持力、外轨对轮缘的弹力.
外轨对轮缘的弹力F提供向心力F=F向
由于该弹力是由轮缘和外轨的挤压产生的,且由于火车质量很大,故轮缘和外轨间的相互作用力很大,易损坏铁轨.
怎么办
请同学们仔细观看视频,观察真实的火车轨道是怎样的?
铁路的弯道——外轨高于内轨
铁路的弯道
θ
FN
在转弯处外轨略高于内轨
火车转弯所需的向心力的方向是在水平方向上还是在与斜面平行的方向上?
G
O
F合
θ
O
G
FN
F合
θ
θ
F合=mg tanθ
轨道对轮缘无挤压,此时火车的速度为多大?
火车转弯时所需的向心力
Fn = m
v2
R
v= gR tanθ
若火车的速度大于或小于这个值时,轨道对轮缘有挤压吗?
2、当 v< gR tanθ :
1、当 v> gR tanθ :
G
FN
θ
轮缘受到外轨向内的弹力
G
FN
θ
F
F
轮缘受到内轨向外的弹力
想一想
若火车的速度大于或小于这个值时,会怎么样呢?
G
Fn
N
h
L
θ
θ
R
此为火车转弯时的安全速度
h、R越大,火车转弯越安全
θ很小时,sinθ=tanθ
此时轮缘与铁轨无弹力作用
(1)、当火车行驶速率 时,Fn=F合,内外轨道都不受挤压,对两轮缘都没有压力
(3)、当火车行驶速率 时, Fn=F合-F侧,内轨道受到挤压对轮缘有侧压力
(2)、当火车行驶速率 时,Fn=F合+F侧,外轨道受到挤压对轮缘有侧压力
在实际生活中,铁路修好后θ(h、L)、r是确定的,所以火车转弯的安全速度也为定值
F合=mg tanθ
总 结
西班牙超速列车脱轨事件
O
mg
FN
f
汽车在水平地面上转弯是什么力提供向心力的呢
汽车转弯
想一想
汽车在水平地面上转弯是什么力提供向心力的呢
O
mg
FN
Ff
汽车在水平路面上转弯所需要的向心力来源:汽车侧向所受的静摩擦力。
O
mg
FN
Ff
当汽车转弯的半径一定时,汽车的速度v越大,所需的向心力也越大,静摩擦力也越大,当静摩擦力为最大静摩擦力时:
O
mg
FN
Ff
由此可见:当汽车转弯时,存在一个安全通过的最大速度,如果超过了这个速度,汽车将发生侧滑现象。
改进措施:
(1)增大转弯半径
(2)增加路面的粗糙程度
(3)最重要的一点:司机应该减速慢行!
(4)增加路面高度差——外高内低
汽车转弯时的措施:
把转弯处的道路修成外高内低。(高速路和赛道)
G
FN
F向
观察下面两幅图片,赛道及告诉公路弯道有什么特点?为什么要这样设计?
路面是倾斜的
外高内低
赛道的设计
N
Fn
mg
思考与赛道类似的例题
例:球沿光滑圆锥内壁在水平面内做匀速圆周运动,如图。试分析向心力的来源。(圆锥摆模型)
N
G
θ
将路面倾斜的原因是让支持力与竖直方向成一角度,这样支持力的水平分力就可以提供部分向心力,减小静摩擦力的负担。
讨论:如果倾斜路面是光滑的,汽车还能转弯吗?
如果能,对速度有什么要求?
结 论
问题:如果倾斜路面是光滑的,汽车还能转弯吗?
如果能,对速度有什么要求?
能,根据上面例题可知,即使没有摩擦力,只靠重力与支持力的合力充当向心力也可以做圆周运动,此时的速度是个定值,假设路面与水平面夹角为θ,则有
问题:如果汽车转弯速度大于这个值呢?或者小于这个值呢?
如果大于这个值,则汽车向上滑,如果小于这个值,则向下滑。
飞机转弯:类似于火车转弯
G
F
Fn
例1、火车以半径R= 900 m转弯,火车质量为8×105kg ,速度为30m/s,火车轨距l=1.4 m,要使火车通过弯道时仅受重力与轨道的支持力,轨道应该垫的高度h?(θ较小时tanθ=sinθ)
FN
mg
F
θ
h
由力的关系得:
由向心力公式得:
由几何关系得:
解:
=0.14m
例2 . 有一列重为100 t的火车,以72 km/h的速率匀速通过一个内外轨一样高的弯道,轨道半径为400 m.(g取10 m/s2)
(1)试计算铁轨受到的侧压力;
(2)若要使火车以此速率通过弯道,且使铁轨受到的侧压力为零,我们可以适当倾斜路基,试计算路基倾斜角度θ的正切值.
FN
mg
汽车过拱形桥
02
拱形桥
(凸形桥)
凹形桥
水平桥
生活中为什么我们经常见到凸桥,很少见到凹桥,相比之下凸桥有哪些优点呢?
凸桥可以让更大的船只通过,利于通航。
发洪水的时候,凸桥在相同的时间内可以流过更多的水,利于泄洪。
更加坚固、美观……
黄石长江大桥
泸定桥
问题1:汽车静止在桥上与通过平桥时,受力怎样?
F压=FN=mg
思考与讨论
问题2:汽车过拱形桥时,在最高点时,车对凸桥的压力又怎样?
mg
FN
v2
R
mg-FN=m
v2
R
FN =mg-m
v2
R
F压=FN =mg-m
汽车对桥的压力小于其所受重力,即处于失重
FN <mg
思考与讨论
v2
R
mg=m
当 FN = 0 时,汽车脱离桥面,做平抛运动,汽车及其中的物体处于完全失重状态。
FN=0 时,汽车的速度为多大?
v2
R
FN =mg-m
问题3:汽车过拱形桥时,运动速度变大,车对凸桥的压力如何变化?
mg
FN
临界速度
思考与讨论
总结:重力及支持力沿半径方向的合力提供向心力。若汽车的速度过大,将会离开桥面做斜抛运动。
若汽车即将离开桥面时,则有FN =0,故
若汽车不在拱形桥的最高点或最低点时,如何分析汽车的运动情况呢?
θ
v2
R
mgcosθ-FN =m
v2
R
FN =mgcosθ-m
v2
R
F压=FN =mgcosθ -m
FN <mg (失重)
v= gR cosθ
可知:桥面所受的压力与夹角θ、车速v都有关;
故汽车过凸形桥时,汽车对桥的压力总小于重力。
问题4:汽车过凹形桥时,在最低点时,车对凹形桥的压力又怎样?
FN
mg
v2
R
FN =mg + m
v2
R
F压=FN =mg + m
v2
R
FN-mg=m
汽车对桥的压力大于其所受重力,即处于超重
若汽车通过凹桥的速度增大,会出现什么情况?
FN >mg
思考与讨论
F压=FN <mg
失重
超重
F压=FN =mg
F压=FN >mg
比较三种桥面受力的情况
凸形桥
泸定桥
过水路面
凹形桥
例1.一辆卡车在丘陵地匀速行驶,地形如图所示,由于轮胎太旧,途中爆胎,爆胎可能性最大的地段应是( )
A. a处 B. b处 C. c处 D. d处
a
b
c
d
D
例2、一辆汽车匀速率通过半径为R的圆弧拱形路面,关于汽车的受力情况,下列说法正确的是( )
A、汽车对路面的压力大小不变,总是等于汽车的重力
B、汽车对路面的压力大小不断发生变化,总是小于汽车所受重力
C、汽车的牵引力不发生变化
D、汽车的牵引力逐渐变小
BD
例3. 一辆质量 m =2 t 的轿车,驶过半径 R = 50 m 的一段凸形桥面,g 取 10 m/s2,求:
(1) 轿车以 10 m/s 的速度通过桥面最高点时,对桥面的压力是多大
(2) 在最高点对桥面的压力等于轿车重力的一半时,车的速度大小是多少
16000 N
航天器中的失重现象
03
地球可以看做一个巨大的拱形桥,桥面的半径就是地球的半径.会不会出现这样的情况:速度大到一定程度时,地面对车的支持力是零?这时驾驶员与座椅之间的压力是多少?……
mg
思考与讨论
地球可以看作一个巨大的拱型桥,其半径就是地球半径R= 6400km,若汽车不断加速,则地面对它的支持力就会变小,汽车速度多大时,支持力会变成零FN=0?
此时司机处于完全失重状态。
由
得
想一想
生活实例:航天器中的失重现象
汽车车速为v,地球半径为R
汽车对桥面的压力为0
G=9.8N/kg,R=6371km
v ≈7900m/s
1、航天器在发射升空(加速上升)时,航天员处在超重还是失重状态?
2、航天器在轨道正常运行(绕地球做匀速圆周运动)时,航天员处在超重还是失重状态?
超重
FN
mg
a
FN-mg =ma
FN>mg
想一想
v2
r
FN =mg-m
航天器绕地球做匀速圆周运动,假设它的线速度的大小为v ,轨道半径近似等于地球半径R ,航天员受到的地球引力近似等于他在地面测得的体重mg .
v= gR
当 时,座舱对航天员的支持力FN=0 ,航天员处于完全失重.
有人把航天器失重的原因说成是它离地球太远,从而摆脱了地球引力,这种说法对吗?
正是由于地球引力的存在,才使航天器连同其中的人和物体绕地球做圆周运动.
v2
R
mg-FN=m
FN <mg
失重
想一想:什么维持近地航天器做圆周运动?
万有引力
有人把航天器失重的原因说成是它离地球太远,从而摆脱了地球引力,这种说法对吗?
正是由于地球引力的存在,才使航天器连同其中的人和物体绕地球做圆周运动.
如果地球的引力突然消失,航天器将做什么样的运动呢?
想一想
离心运动
04
O
F合 = mω2r,
F合<mω2r ,
F 合= 0 ,
1、定义:做匀速圆周运动的物体,在所受合力突然消失,或者不足以提供圆周运动所需的向心力时,做逐渐远离圆心的运动,这种运动叫做离心运动.
2、条件:
0 ≤F合<mω2r
供<需
物体沿切线方向飞出远离圆心
物体做匀速圆周运动
物体做逐渐远离圆心的运动
(1) 当 F=mω2r 时,物体做匀速圆周运动;
(2) 当 F=0 时,物体沿切线方向飞出;
(3) 当 F<mω2r 时,物体逐渐远离圆心;
(4) 当 F>mω2r 时,物体逐渐靠近圆心。
理解:
(1)物体做离心运动,并不是受到“离心力”作用,更不是“离心力”大于向心力,而是外界提供的向心力不足或突然消失。
(2)离心运动不是沿着半径背离圆心的运动,而是沿着切线或曲线离心的运动。
结 论
离心运动的应用
离心抛掷
离心甩干
离心脱水
离心分离
(1)离心运动的应用
①甩干雨伞上的水滴
②链球运动
在田径比赛中,链球项目就是得用离心现象来实现投掷的。链球的投掷是通过预摆和旋转来完成的,运动员手持链球链条的一端,在链球高速旋转时,突然松手,拉力消失,链就沿切线方向飞出去。
在雨天,我们可以通过旋转雨伞
的方法甩干雨伞上的水滴,旋转时,当转动快到一定的程度时,水滴和雨伞之间的附着力满足不了水滴做圆周运动所需的向心力,水滴就会做远离圆心的运动而被甩出去。
把湿布块放在离心干燥器的金属网笼里,网笼转得比较慢时,水滴跟物体的附着力 F足以提供所需要的向心力,使水滴做圆周运动,当网笼转的比较快时,附着力 F 不足以提供所需要的向心力,于是水滴做离心运动,穿过网孔,飞到网笼外面。洗衣机的脱水筒也是利用离心运动把湿衣服甩干的。
③离心干燥器
o
F
v
、制作“棉花”糖的原理:
内筒与洗衣机的脱水筒相似,往内筒加入白砂糖,加热使糖熔化成糖汁,内筒高速旋转,黏稠的糖汁就做离心运动,从内筒壁的小孔飞散出去,成为丝状,到达温度较低的外筒就会迅速冷却凝固,变得纤细雪白,像一团团棉花。
“离心浇铸”技术
模具绕一固定轴旋转,当达到500转每分时,将融化了的液态金属倒入其中,它将以巨大的惯性离心力向模具壁紧压,同时夹杂在液态金属里的气体和熔渣,由于其密度远小于液态的金属,因此它们将从金属里被分离出来。按此法浇铸出的金属零件密实、均匀、不含气泡和裂痕,大大提高了使用寿命。
啤酒何以清澈透亮?
原来这也与离心分离密切相关。因为麦汁中含有一种极不稳定的冷凝固物,应尽量减少其含量才能保证啤酒不出现冷混浊现象。然而,这种冷凝固物的粒子极为微小,直径仅有0.1―0.5微米,很难除净。但若采用高速离心机进行分离处理,就比较容易实现净化。因为这种粒子虽然微小,但由于存在密度差,一旦进入强大的离心力场后,二者立即“分道扬镳”,从而可以很容易地把冷凝固粒子剔除。
从蔗糖水溶液中分离蔗糖,也需依靠离心沉降方法 。
当离心机转得比较慢时,缩口的阻力 F 足以提供所需的向心力,缩口上方的水银柱做圆周运动。 当离心机转得相当快时,阻力 F 不足以提供所需的向心力,水银柱做离心运动而进入玻璃泡内。
离心沉淀器
要使原来作匀速圆周运动的物体作离心运动,该怎么办?
1、提高转速,使所需向心力增大到大于物体所受合外力.
2、减小合外力或使其消失.
供=需
供<需
想一想
赛道设计
离心运动的危害与防止
交通限速
O
F静
v
在水平公路上行驶的汽车,转弯时所需的向心力是由车轮与路面的静摩擦力提供的。如果转弯时速度过大,所需向心力Fn大于最大静摩擦力Fmax (Fmax不足以提供向心力),汽车将做离心运动而造成交通事故.因此,在公路弯道处,车辆行驶不允许超过规定的速度.
当 时,汽车做离心运动
Fmax<m
v2
r
离心运动的防止
高速转动的砂轮、飞轮等,都不得超过允许的最大转速。转速过高时,砂轮、飞轮内部分子间的相互作用力不足以提供所需向心力,离心运动会使它们破裂,酿成事故.
O
F
v
为什么转动的砂轮、飞轮等都要限速?
要防止离心现象发生,该怎么办?
1、减小物体运动的速度,使物体作圆周运动时所需的向心力减小.
2、增大合外力,使其达到物体作圆周运动时所需的向心力.
供<需
供=需
想一想
摩托车飞车走壁,请分析受力情况,解释现象
1. 如图所示,光滑水平面上,质量为 m 的小球在拉力 F 作用下做匀速圆周运动。若小球运动到 P 点时,拉力 F 发生变化,下列关于小球运动情况的说法中正确的是( )
BC
若拉力突然变大,小球将沿轨迹
Pb 做离心运动
B. 若拉力突然变小,小球将沿轨迹
Pb 做离心运动
C. 若拉力突然消失,小球将沿轨迹
Pa 做离心运动
D. 若拉力突然变小,小球将沿轨迹
Pc 做近心运动
2. 如图所示,光滑圆盘中心有一个小孔,用细绳穿过小孔,两端各系一小球 A、B,A、B 等质量,盘上的小球 A 做半径为 r = 20 cm 的匀速圆周运动,若要保持 B 球静止,A 球的角速度多大?
A
B
F
F
解:对于 A,根据牛顿第二定律
F = mω2r
对于 B,F = mg
解得
3.下列有关洗衣机脱水筒的脱水原理说法正确的是 ( )
A.水滴受离心力作用,而沿背离圆心的方向甩出
B.水滴受到向心力,由于惯性沿切线方向甩出
C.水滴受到的离心力大于它受到的向心力,从而沿切线方向甩出
D.水滴与衣服间的附着力小于它所需的向心力,于是沿切线方向甩出
D
4.人造地球卫星绕地球做匀速圆周运动,下列说法中正确的有 ( )
A.可以用天平测量物体的质量
B.可以用水银气压计测舱内的气压
C.可以用弹簧测力计测拉力
D.在卫星内将重物挂于弹簧测力计上,弹簧测力计示数为零,但重物仍受地球的引力
CD
课堂小结
火车转弯
汽车过桥
失重现象
离心运动
当 v< gR tanθ :
当 v> gR tanθ :轮缘受到外轨向内的弹力
轮缘受到内轨向外的弹力
FN
做离心运动的条件:
典例分析
05
【练习1】(2022秋·重庆市育才中学高一期末)(多选)在修筑铁路时,弯道处的外轨会略高于内轨。如图所示,当火车以规定的行驶速度转弯时,内、外轨均不会受到轮缘的挤压,设此时的速度大小为v,重力加速度为g,两轨所在面的倾角为θ,则( )
A.该弯道的半径
B.当火车质量改变时,规定的行驶速度大小不变
C.当火车速率大于v时,内轨将受到轮缘的挤压
D.当火车速率小于v时,外轨将受到轮缘的挤压
【参考答案】AB
【练习2】汽车在过凹凸路面时,都会做减速操作,如图A、B分别是一段凹凸路面的最高点和最低点,若把汽车视作质点,则下列说法正确的是( )
A.汽车行驶到A点时,处于超重状态,如果采取加速操作会使车胎受到更大的压力
B.汽车行驶到B点时,处于超重状态,如果采取加速操作会使汽车飞离路面
C.汽车行驶到A点时,处于失重状态,如果采取减速操作会增加车胎与路面间的弹力,使得行驶更加稳定安全
D.汽车行驶到B点时,处于失重状态,如果采取减速操作会增加车胎与路面间的弹力,使得行驶更加稳定安全
【参考答案】C
【练习3】翻滚过山车是一种非常刺激而有趣的游乐项目。如图甲所示,小刚同学所坐的翻滚过山车正在下行中,如图乙所示,他此时所做的运动及所受合力的可能方向分别是( )
A.匀速圆周运动、沿F1方向
B.匀速圆周运动、沿F2方向
C.加速圆周运动、沿F3方向
D.减速圆周运动、沿F2方向
【参考答案】C
【练习4】(2023秋·长春外国语高一期末)(多选)若将短道速滑运动员在弯道转弯的过程看成在水平冰面上的一段匀速圆周运动,转弯时冰刀嵌入冰内从而使冰刀受与冰面夹角为θ(蹬冰角)的支持力,不计一切摩擦,弯道半径为R,重力加速度为g。以下说法正确的是( )
A.地面对运动员的作用力与重力与重力大小相等
B.武大靖转弯时速度的大小为
C.若武大靖转弯速度变大则需要减小蹬冰角
D.武大靖做匀速圆周运动,他所受合外力保持不变
【参考答案】BC
【练习5】气嘴灯安装在自行车的气嘴上,骑行速度在一定范围内会发光。一种气嘴灯的感应装置结构如图所示,一重物套在光滑杆上,并与弹簧连接,重物上的触点M与固定在B端的触点N接触后,LED灯就会发光。则下列说法正确的是( )
A.气嘴灯运动至最低点时处于失重状态
B.当车速较小时,重物的重力大于弹簧的弹力,使得触点MN接触,LED灯发光
C.当车速较大时,重物受到的合力不足以提供所需向心力,重物做离心运动,使得触点MN接触,LED灯发光
D.气嘴灯做圆周运动时,重物
受到重力、弹力和向心力的作用
【参考答案】C
感谢您的耐心聆听
I'd like to finish by saying how grateful I am for your attention.
