华东师大版数学七年级下册8.1 认识不等式课件(共24张PPT)
文档属性
| 名称 | 华东师大版数学七年级下册8.1 认识不等式课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-18 10:02:30 | ||
图片预览






文档简介
(共24张PPT)
8.1 认识不等式
第八章 一元一次不等式
逐点
学练
本节小结
作业提升
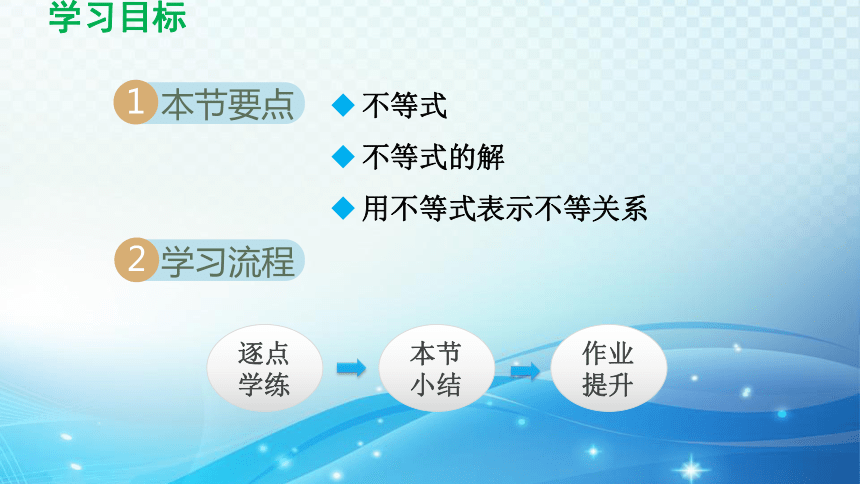
学习目标
本节要点
1
学习流程
2
不等式
不等式的解
用不等式表示不等关系
感悟新知
知识点
不等式
1
1.不等式: 用不等号“<”或“>”表示不等关系的式子,叫做不等式 .
感悟新知
特别提醒
判断一个式子是否为不等式,关键是看所给式子是否含不等号;
不等号具有方向性,不等号两边的数(或式子)不能随意交换.
不等号的“开口”所对的数较大,不等号的 “尖头”所对的数较小.
感悟新知
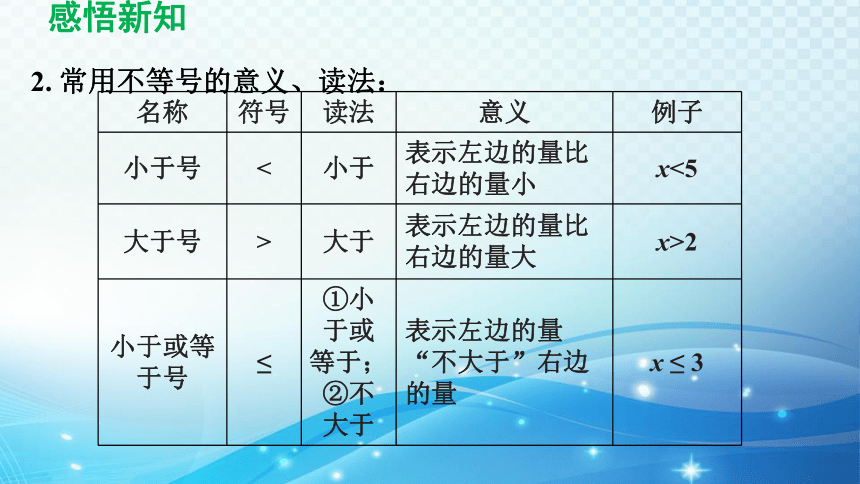
2. 常用不等号的意义、读法:
名称 符号 读法 意义 例子
小于号 < 小于 表示左边的量比右边的量小 x<5
大于号 > 大于 表示左边的量比右边的量大 x>2
小于或等于号 ≤ ①小于或等于;
②不大于 表示左边的量“不大于”右边的量 x ≤ 3
感悟新知
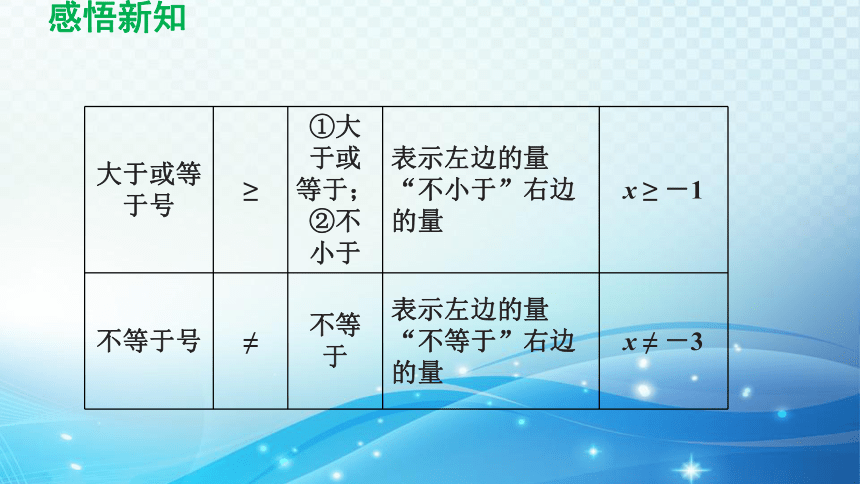
大于或等于号 ≥ ①大于或等于;
②不小于 表示左边的量“不小于”右边的量 x ≥ -1
不等于号 ≠ 不等于 表示左边的量“不等于”右边的量 x ≠ -3
感悟新知
判断下列各式哪些是等式,哪些是不等式,哪些既不是等式也不是不等式 .
(1) x+y; (2) 3x>7;
(3) 5=2x+3; (4) x2>0;
(5) 2x - 3y=1; (6) 5÷2;
(7) 2>7
例1
感悟新知
解: (3) (5)是等式, (2) (4) (7)是不等式, (1) (6) 既不是等式也不是不等式 .
解题秘方:紧扣等式、不等式的定义进行识别,关键是看式子是否含有等号或不等号 .
1-1. 给出下列各式:① - 3<0;② 4x+3y>0;③ 3x=5;④ x2 - xy+y2;⑤ x+2> - 7. 其中不等式的个数是( )
A. 5 B. 4
C. 3 D. 2
C
感悟新知
知识点
不等式的解
2
1. 不等式的解: 能使不等式成立的未知数的值,叫做不等式的解 .
感悟新知
2. 不等式的解与一元一次方程的解的区别:
(1)不等式的解是不确定的,一个不等式如果有解,一般会有无数个解,而一个一元一次方程的解,一般只有一个;
(2)不等式的解可以有多个,它是指某一特定范围内的所有的数,用它代替不等式中的未知数,不等式一定成立 .
感悟新知
特别解读
只要是能使不等式成立的未知数的值都是不等式的解.关键是使不等式成立,个数不能确定.
感悟新知
判断下列说法是否正确:
(1) 4 是不等式 x+2>1 的解;
(2) 6 不是不等式 y - 1<6 的解;
(3)所有小于 2 的整数都是不等式 x+3<5 的解 .
例2
感悟新知
解题秘方:紧扣不等式的解的定义进行判断:把数值代入不等式中,看不等式是否成立 .
解: (1)把 x=4 代入不等式的左边,得左边 =6>1,
所以 x=4 是不等式 x+2>1 的解,故(1)的说法正确 .
(2)把 y=6 代入不等式的左边,得左边 =5<6,
所以 y=6 是不等式 y - 1<6 的解,故(2)的说法不正确 .
(3)因为所有小于 2 的整数都能使 x+3<5 成立,
所以(3)的说法正确 .
2-1.下列各数中, 是不等式 x>3 的解的是( )
A. - 3 B. 0
C. 3 D. 5
D
感悟新知
知识点
用不等式表示不等关系
3
1.列不等式: 用不等式表示不等关系叫做列不等式 .
感悟新知
2. 列不等式通常有以下两种情形:
(1)根据数量关系列不等式;
(2)根据实际问题列不等式 .
感悟新知
3. 列不等式的步骤:
(1)认真审题,分清题目中包含的数量间的大小关系;
(2)将题目中的不同数量用代数式表示出来;
(3)用不等号以及运算符号连接所列的代数式,列出不等式 .
感悟新知
常见的不等式基本语言与符号表示:
不等式基本语言 符号表示
a 是正数 a>0
a 是负数 a<0
a 是非正数 a ≤ 0
a 是非负数 a ≥ 0
a, b 同号 ab>0
a, b 异号 ab<0
感悟新知
用不等式表示:
(1) a 的一半与 3 的和大于 5;
(2) x 的 3 倍与 1 的差小于 2;
(3) a 的 与 1 的差是正数;
(4) m 与 2 的差是负数 .
例3
感悟新知
解题秘方:紧扣不等关系中的关键词语列出不等式 .
解: (1) a+3>5. (2) 3x - 1<2.
(3) a - 1>0. (4) m - 2<0.
3-1.用不等式表示下列数量之间的关系:
(1) x2 是非负数;
(2)两数 m,n 积的 2 倍不大于这两数的平方和;
(3)某客车坐有x 人,其最大载客量为40 人;
(4)某校男子跳高纪录是 1.75 m,小强在今年的运动会上跳了 x m,打破了校纪录.
解:(1)x2≥0.(2)2mn≤m2+n2.(3)x≤40.(4)x>1.75.
认识不等式
词语
不等式
建模
大于、小于、
不等于
实际问题
转化
>、<、≠
不等式的解
请完成教材课后作业
作业提升
8.1 认识不等式
第八章 一元一次不等式
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
不等式
不等式的解
用不等式表示不等关系
感悟新知
知识点
不等式
1
1.不等式: 用不等号“<”或“>”表示不等关系的式子,叫做不等式 .
感悟新知
特别提醒
判断一个式子是否为不等式,关键是看所给式子是否含不等号;
不等号具有方向性,不等号两边的数(或式子)不能随意交换.
不等号的“开口”所对的数较大,不等号的 “尖头”所对的数较小.
感悟新知
2. 常用不等号的意义、读法:
名称 符号 读法 意义 例子
小于号 < 小于 表示左边的量比右边的量小 x<5
大于号 > 大于 表示左边的量比右边的量大 x>2
小于或等于号 ≤ ①小于或等于;
②不大于 表示左边的量“不大于”右边的量 x ≤ 3
感悟新知
大于或等于号 ≥ ①大于或等于;
②不小于 表示左边的量“不小于”右边的量 x ≥ -1
不等于号 ≠ 不等于 表示左边的量“不等于”右边的量 x ≠ -3
感悟新知
判断下列各式哪些是等式,哪些是不等式,哪些既不是等式也不是不等式 .
(1) x+y; (2) 3x>7;
(3) 5=2x+3; (4) x2>0;
(5) 2x - 3y=1; (6) 5÷2;
(7) 2>7
例1
感悟新知
解: (3) (5)是等式, (2) (4) (7)是不等式, (1) (6) 既不是等式也不是不等式 .
解题秘方:紧扣等式、不等式的定义进行识别,关键是看式子是否含有等号或不等号 .
1-1. 给出下列各式:① - 3<0;② 4x+3y>0;③ 3x=5;④ x2 - xy+y2;⑤ x+2> - 7. 其中不等式的个数是( )
A. 5 B. 4
C. 3 D. 2
C
感悟新知
知识点
不等式的解
2
1. 不等式的解: 能使不等式成立的未知数的值,叫做不等式的解 .
感悟新知
2. 不等式的解与一元一次方程的解的区别:
(1)不等式的解是不确定的,一个不等式如果有解,一般会有无数个解,而一个一元一次方程的解,一般只有一个;
(2)不等式的解可以有多个,它是指某一特定范围内的所有的数,用它代替不等式中的未知数,不等式一定成立 .
感悟新知
特别解读
只要是能使不等式成立的未知数的值都是不等式的解.关键是使不等式成立,个数不能确定.
感悟新知
判断下列说法是否正确:
(1) 4 是不等式 x+2>1 的解;
(2) 6 不是不等式 y - 1<6 的解;
(3)所有小于 2 的整数都是不等式 x+3<5 的解 .
例2
感悟新知
解题秘方:紧扣不等式的解的定义进行判断:把数值代入不等式中,看不等式是否成立 .
解: (1)把 x=4 代入不等式的左边,得左边 =6>1,
所以 x=4 是不等式 x+2>1 的解,故(1)的说法正确 .
(2)把 y=6 代入不等式的左边,得左边 =5<6,
所以 y=6 是不等式 y - 1<6 的解,故(2)的说法不正确 .
(3)因为所有小于 2 的整数都能使 x+3<5 成立,
所以(3)的说法正确 .
2-1.下列各数中, 是不等式 x>3 的解的是( )
A. - 3 B. 0
C. 3 D. 5
D
感悟新知
知识点
用不等式表示不等关系
3
1.列不等式: 用不等式表示不等关系叫做列不等式 .
感悟新知
2. 列不等式通常有以下两种情形:
(1)根据数量关系列不等式;
(2)根据实际问题列不等式 .
感悟新知
3. 列不等式的步骤:
(1)认真审题,分清题目中包含的数量间的大小关系;
(2)将题目中的不同数量用代数式表示出来;
(3)用不等号以及运算符号连接所列的代数式,列出不等式 .
感悟新知
常见的不等式基本语言与符号表示:
不等式基本语言 符号表示
a 是正数 a>0
a 是负数 a<0
a 是非正数 a ≤ 0
a 是非负数 a ≥ 0
a, b 同号 ab>0
a, b 异号 ab<0
感悟新知
用不等式表示:
(1) a 的一半与 3 的和大于 5;
(2) x 的 3 倍与 1 的差小于 2;
(3) a 的 与 1 的差是正数;
(4) m 与 2 的差是负数 .
例3
感悟新知
解题秘方:紧扣不等关系中的关键词语列出不等式 .
解: (1) a+3>5. (2) 3x - 1<2.
(3) a - 1>0. (4) m - 2<0.
3-1.用不等式表示下列数量之间的关系:
(1) x2 是非负数;
(2)两数 m,n 积的 2 倍不大于这两数的平方和;
(3)某客车坐有x 人,其最大载客量为40 人;
(4)某校男子跳高纪录是 1.75 m,小强在今年的运动会上跳了 x m,打破了校纪录.
解:(1)x2≥0.(2)2mn≤m2+n2.(3)x≤40.(4)x>1.75.
认识不等式
词语
不等式
建模
大于、小于、
不等于
实际问题
转化
>、<、≠
不等式的解
请完成教材课后作业
作业提升
