有理数的乘方[上学期]
图片预览

文档简介
1.5.1有理数的乘方
备课人:严均亮 修改人: 修改时间:
教学目标
1.理解有理数乘方、幂、指数、底数等概念;
2.理解乘方的意义,掌握有理数乘方的运算;
3.通过对乘方意义的理解,培养学生观察、比较、分析、归纳、概括的能力,渗透转化思想。
教学重点与难点
重点:理解乘方的意义,掌握有理数乘方的运算;
难点:理解有理数乘方、幂、指数、底数等概念,并合理运算;
关键:弄清楚底数、指数、幂等概念,注意区别与的意义。
教学过程
一、复习与检查预习(5分钟)
1、几个不等于零的有理数相乘,积的符号是怎么确定的?
答:几个不等于零的有理数相乘,积的符号由负因数的个数确定,当负因数的个数为奇数时,积为负;当负因数的个数是偶数时,积为正。
2、正方形的边长为2,它的面积是多少?棱长为2的正方体,它的体积是多少?
答:;。
二、导入新课,揭示目标:(2分钟)
提问并引导学生回答:在小学里我们学过一个数的平方和立方是如何定义的?怎样表示?
边长为a的正方形的面积是,棱长为a的正方体的体积是。
记作a2,读作a的平方(或a的2次方),即;a·a·a记作a3,读作a的立方(或a的3次方),即. 像这种相同的有理数相乘的运算,就是我们这节课的学习内容-------揭示目标。
三、讲授新课(18分钟)
让我们再看下面的例子:
(多媒体演示细胞分裂过程)某种细胞,每过30分钟便由1个分裂成2个,经过5小时,这种细胞由1个分裂成多少个?
1个细胞30分钟分裂成2个,1个小时后分裂成2×2个,1.5小时后分裂成2×2×2个,…,5小时后要分裂10次,分裂成2×2×2×…×2=1024个
10个2
为了简便可将2×2×2×…×2记作210.
10个2
引导学生归纳乘方的意义:
一般地,n个相同的因数a相乘,即a·a·…·a,记作an,读作a的n次方.
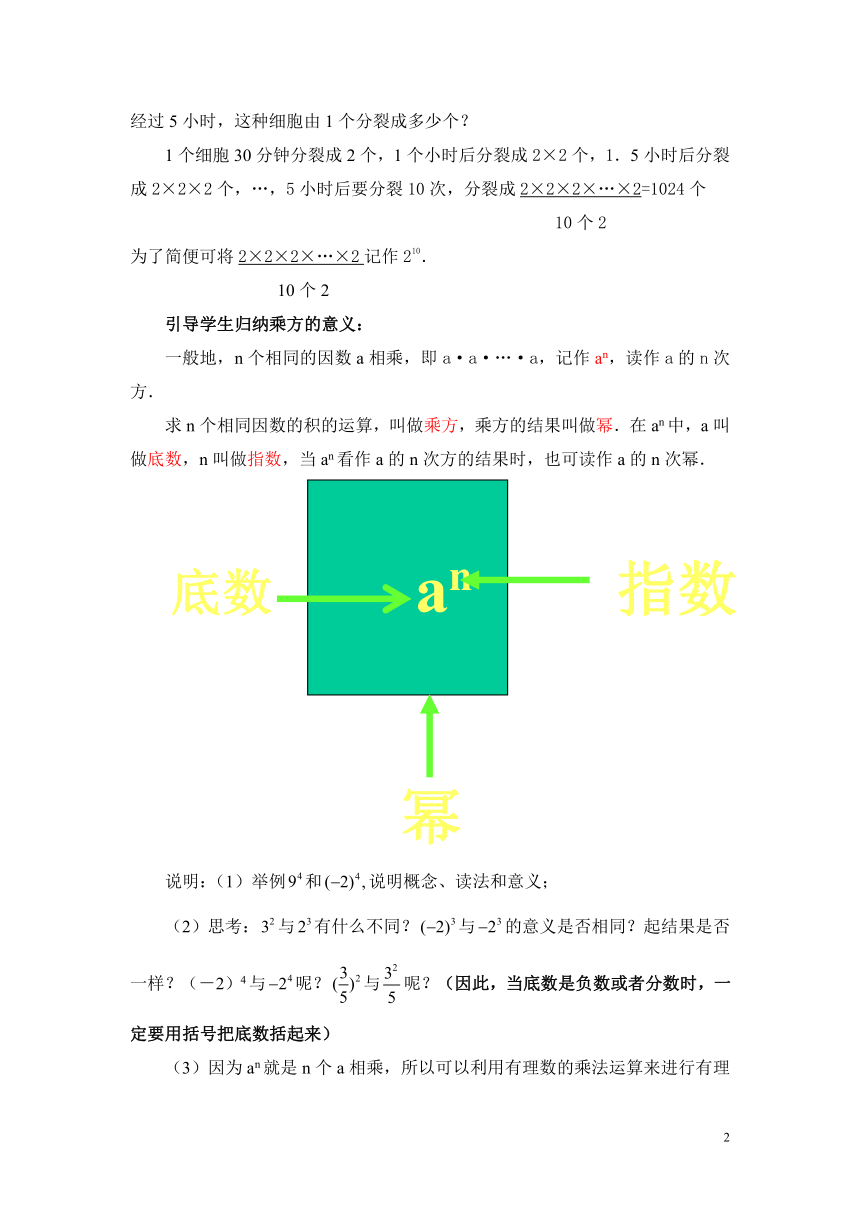
求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂.在an中,a叫做底数,n叫做指数,当an看作a的n次方的结果时,也可读作a的n次幂.
说明:(1)举例和说明概念、读法和意义;
(2)思考:与有什么不同?与的意义是否相同?起结果是否一样?(-2)4与呢?与呢?(因此,当底数是负数或者分数时,一定要用括号把底数括起来)
(3)因为an就是n个a相乘,所以可以利用有理数的乘法运算来进行有理数的乘方运算;
(4)乘方是一种运算,幂是乘方运算的结果.
例题讲解
例1 (1)(-4)3; (2)(-2)4; (3)-24.
(4) (5) (6)
分析:(1)计算时仍然是要先确定符号,再确定绝对值;
(2)注意(-2)4与-24的区别.
根据上面的例题(也说明一下怎么根据有理数的乘法法则)得出有理数乘方的符号规律:
分析(1)(2): 负数的奇次幂是负数,负数的偶次幂是正数;
分析(3)(4): 正数的任何次幂都是正数;
0的任何次幂都是0.
四、巩固练习:(10分钟)
1. 试一试从1开始你能迅速连续说出多少正整数的平方?
处理:让学生口答
2. 教材P53练习1
处理:学生先做,再板演和点评。
3. 计算:
(1)()3; (2)(-)3; (3)(-)4;
(4)-; (5)-22×(-3)2; (6)-22+(-3)2.
处理:同上
五、小结(2分钟)
(1)引导学生作知识小结:理解有理数乘方的意义,运用有理数乘方运算法则进行有理数乘方的运算,熟知底数、指数、和幂三个基本概念.
(2)(选择:)教师扩展:首先,有理数的乘方就是几个相同因数积的运算,可以运用有理数乘方法则进行符号的确定和幂的求值.乘方的含义:①表示一种运算;②表示运算的结果.乘方的读法:①当an表示运算时,读作a的n次方;②当an表示运算结果时,读作a的n次幂.乘方的符号法则:①正数的任何次幂都是正数;②零的任何次幂都是零;③负数的偶次幂是正数,奇次幂是负数.注意(-a)n
与-an及()n与的区别和联系.
六、小测(8分钟)
1、填空选择
(1)在(-2)6中,指数为 ,底数为 .
(2)在-26中,指数为 ,底数为 .
(3)若a2=16,则a= .
(4)下列说法正确的是( )
A.平方得9的数是3 B.平方得-9的数是-3
C.一个数的平方只能是正数 D.一个数的平方不能是负数
(5)下列运算正确的是( )
A.-24=16 B.-(-2)2=-4
C.(-)2=- D.(-)2=-
(6)下列各组数中,不相等的是( )
A.(-3)2与-32 B.(-3)2与32
C.(-2)3与-23 D.
2、计算:
①()×(-)×(-)2, -(-)2, -;
②(-1)2003,3×22, -42×(-4)2, -23÷(-2)3;
.
七、作业布置
1、课本58页习题1.5第1题,第60页第12题。
2、预习课本53---54页,完成54页练习和导学47页知识回顾
八、板书设计
投影 课题 作业 知识点 例题 学生板书 学生板书 学生板书
指数
幂
底数
an
PAGE
4
备课人:严均亮 修改人: 修改时间:
教学目标
1.理解有理数乘方、幂、指数、底数等概念;
2.理解乘方的意义,掌握有理数乘方的运算;
3.通过对乘方意义的理解,培养学生观察、比较、分析、归纳、概括的能力,渗透转化思想。
教学重点与难点
重点:理解乘方的意义,掌握有理数乘方的运算;
难点:理解有理数乘方、幂、指数、底数等概念,并合理运算;
关键:弄清楚底数、指数、幂等概念,注意区别与的意义。
教学过程
一、复习与检查预习(5分钟)
1、几个不等于零的有理数相乘,积的符号是怎么确定的?
答:几个不等于零的有理数相乘,积的符号由负因数的个数确定,当负因数的个数为奇数时,积为负;当负因数的个数是偶数时,积为正。
2、正方形的边长为2,它的面积是多少?棱长为2的正方体,它的体积是多少?
答:;。
二、导入新课,揭示目标:(2分钟)
提问并引导学生回答:在小学里我们学过一个数的平方和立方是如何定义的?怎样表示?
边长为a的正方形的面积是,棱长为a的正方体的体积是。
记作a2,读作a的平方(或a的2次方),即;a·a·a记作a3,读作a的立方(或a的3次方),即. 像这种相同的有理数相乘的运算,就是我们这节课的学习内容-------揭示目标。
三、讲授新课(18分钟)
让我们再看下面的例子:
(多媒体演示细胞分裂过程)某种细胞,每过30分钟便由1个分裂成2个,经过5小时,这种细胞由1个分裂成多少个?
1个细胞30分钟分裂成2个,1个小时后分裂成2×2个,1.5小时后分裂成2×2×2个,…,5小时后要分裂10次,分裂成2×2×2×…×2=1024个
10个2
为了简便可将2×2×2×…×2记作210.
10个2
引导学生归纳乘方的意义:
一般地,n个相同的因数a相乘,即a·a·…·a,记作an,读作a的n次方.
求n个相同因数的积的运算,叫做乘方,乘方的结果叫做幂.在an中,a叫做底数,n叫做指数,当an看作a的n次方的结果时,也可读作a的n次幂.
说明:(1)举例和说明概念、读法和意义;
(2)思考:与有什么不同?与的意义是否相同?起结果是否一样?(-2)4与呢?与呢?(因此,当底数是负数或者分数时,一定要用括号把底数括起来)
(3)因为an就是n个a相乘,所以可以利用有理数的乘法运算来进行有理数的乘方运算;
(4)乘方是一种运算,幂是乘方运算的结果.
例题讲解
例1 (1)(-4)3; (2)(-2)4; (3)-24.
(4) (5) (6)
分析:(1)计算时仍然是要先确定符号,再确定绝对值;
(2)注意(-2)4与-24的区别.
根据上面的例题(也说明一下怎么根据有理数的乘法法则)得出有理数乘方的符号规律:
分析(1)(2): 负数的奇次幂是负数,负数的偶次幂是正数;
分析(3)(4): 正数的任何次幂都是正数;
0的任何次幂都是0.
四、巩固练习:(10分钟)
1. 试一试从1开始你能迅速连续说出多少正整数的平方?
处理:让学生口答
2. 教材P53练习1
处理:学生先做,再板演和点评。
3. 计算:
(1)()3; (2)(-)3; (3)(-)4;
(4)-; (5)-22×(-3)2; (6)-22+(-3)2.
处理:同上
五、小结(2分钟)
(1)引导学生作知识小结:理解有理数乘方的意义,运用有理数乘方运算法则进行有理数乘方的运算,熟知底数、指数、和幂三个基本概念.
(2)(选择:)教师扩展:首先,有理数的乘方就是几个相同因数积的运算,可以运用有理数乘方法则进行符号的确定和幂的求值.乘方的含义:①表示一种运算;②表示运算的结果.乘方的读法:①当an表示运算时,读作a的n次方;②当an表示运算结果时,读作a的n次幂.乘方的符号法则:①正数的任何次幂都是正数;②零的任何次幂都是零;③负数的偶次幂是正数,奇次幂是负数.注意(-a)n
与-an及()n与的区别和联系.
六、小测(8分钟)
1、填空选择
(1)在(-2)6中,指数为 ,底数为 .
(2)在-26中,指数为 ,底数为 .
(3)若a2=16,则a= .
(4)下列说法正确的是( )
A.平方得9的数是3 B.平方得-9的数是-3
C.一个数的平方只能是正数 D.一个数的平方不能是负数
(5)下列运算正确的是( )
A.-24=16 B.-(-2)2=-4
C.(-)2=- D.(-)2=-
(6)下列各组数中,不相等的是( )
A.(-3)2与-32 B.(-3)2与32
C.(-2)3与-23 D.
2、计算:
①()×(-)×(-)2, -(-)2, -;
②(-1)2003,3×22, -42×(-4)2, -23÷(-2)3;
.
七、作业布置
1、课本58页习题1.5第1题,第60页第12题。
2、预习课本53---54页,完成54页练习和导学47页知识回顾
八、板书设计
投影 课题 作业 知识点 例题 学生板书 学生板书 学生板书
指数
幂
底数
an
PAGE
4
