2021-2022学年福建省八年级下学期人教版数学第十八章 平行四边形练习题期末试题选编(含解析)
文档属性
| 名称 | 2021-2022学年福建省八年级下学期人教版数学第十八章 平行四边形练习题期末试题选编(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-18 10:40:42 | ||
图片预览



文档简介
第十八章:平行四边形
一、单选题
1.(2022春·福建龙岩·八年级统考期末)小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
A.①,② B.①,④ C.③,④ D.②,③
2.(2022春·福建宁德·八年级统考期末)如图,四边形ABCD是平行四边形,E是AB延长线上一点,若∠EBC=50°,则∠D的度数为( )
A.50° B.100° C.130° D.150°
3.(2022春·福建龙岩·八年级统考期末)下列给出的条件能判定四边形为平行四边形的是( )
A.AB//CD, B.,
C., D.,
4.(2022春·福建福州·八年级统考期末)下列条件中,能判定四边形是平行四边形的是( )
A.一组对边平行 B.对角线互相平分
C.一组对边相等 D.对角线互相垂直
5.(2022春·福建福州·八年级统考期末)若顺次连接平行四边形各边中点所得四边形必定是( )
A.矩形 B.平行四边形 C.正方形 D.菱形
6.(2022春·福建南平·八年级统考期末)如图,在平面直角坐标系中,□AOBC的顶点B在x轴上,OA=2,∠AOB =60°, OP平分∠AOB交AC边于点P,则点P的坐标是是( )
A. B.
C. D.
7.(2022春·福建泉州·八年级统考期末)如图,四边形中,ADBC,,,.若点是线段的中点,则的长为( )
A. B.2 C. D.3
8.(2022春·福建福州·八年级统考期末)如图,在△ABC中,E,F分别为AC,BC中点,若AB=6,BC=7,AC=8,则EF=( )
A.3 B.3.5 C.4 D.4.5
9.(2022春·福建厦门·八年级统考期末)如图,在中,D,E分别是的中点,点F在延长线上,添加一个条件使四边形为平行四边形,则这个条件是( )
A. B. C. D.
10.(2022春·福建福州·八年级统考期末)要判断一个四边形的窗框是否为矩形,可行的测量方案是( )
A.测量两组对边是否相等
B.测量对角线是否相等
C.测量对角线是否互相平分
D.测量对角线交点到四个顶点的距离是否都相等
11.(2022春·福建泉州·八年级统考期末)如图,矩形的两条对角线相交于点,已知,,则矩形对角线的长为( )
A. B. C. D.
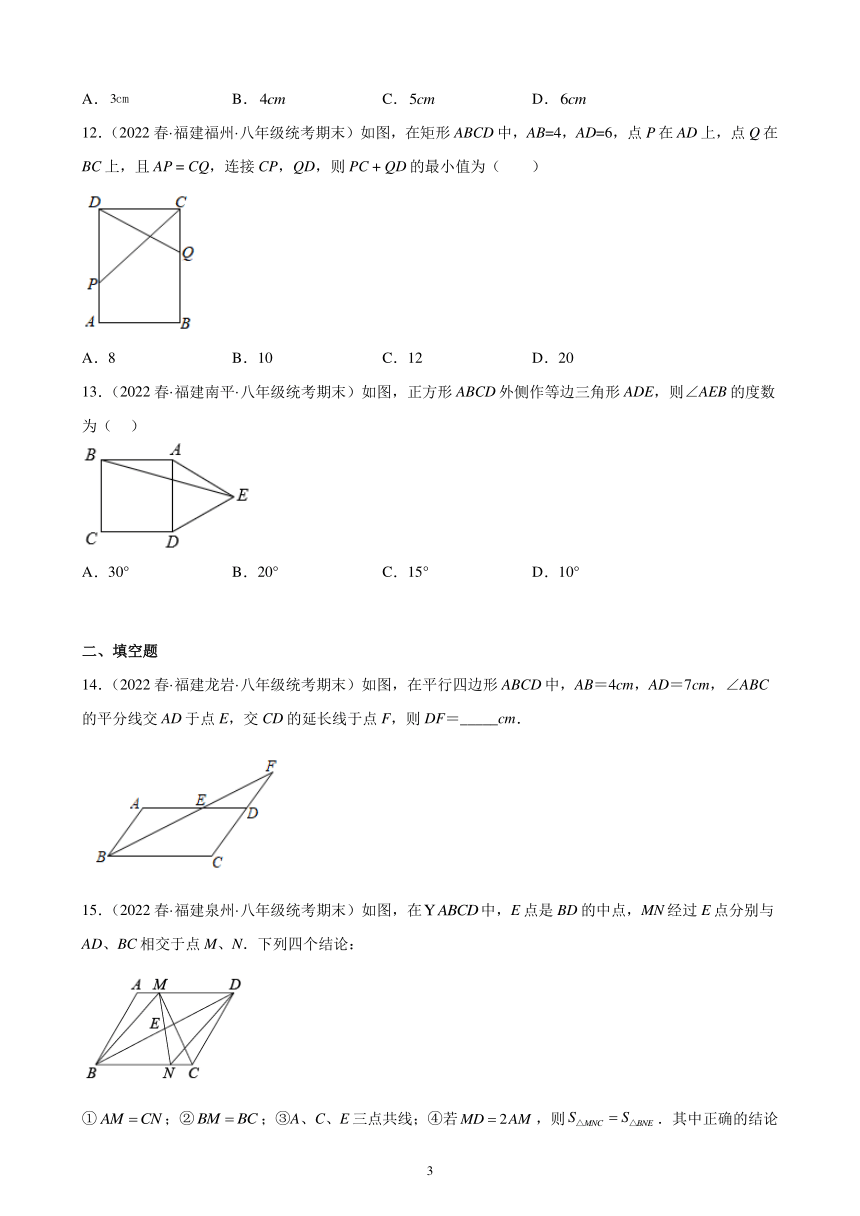
12.(2022春·福建福州·八年级统考期末)如图,在矩形ABCD中,AB=4,AD=6,点P在AD上,点Q在BC上,且AP = CQ,连接CP,QD,则PC + QD的最小值为( )
A.8 B.10 C.12 D.20
13.(2022春·福建南平·八年级统考期末)如图,正方形ABCD外侧作等边三角形ADE,则∠AEB的度数为( )
A.30° B.20° C.15° D.10°
二、填空题
14.(2022春·福建龙岩·八年级统考期末)如图,在平行四边形ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=_____cm.
15.(2022春·福建泉州·八年级统考期末)如图,在中,E点是BD的中点,MN经过E点分别与AD、BC相交于点M、N.下列四个结论:
①;②;③A、C、E三点共线;④若,则.其中正确的结论有____.(写出所有正确结论的序号)
16.(2022春·福建漳州·八年级统考期末)在四边形中,现给出下列结论:
①若,,则四边形是平行四边形;
②若,,则四边形是平行四边形;
③若,,则四边形是平行四边形;
④若,,则四边形是平行四边形.
其中正确的结论是____________.(写出所有正确结论的序号)
17.(2022春·福建泉州·八年级统考期末)如图,在四边形ABCD中,AB∥CD,∠D=2∠B,若AD=3,AB=5,则CD=______.
18.(2022春·福建三明·八年级统考期末)如图,A,B两处被池塘隔开,为了测量A,B两处的距离,在AB外选一适当的点C,连接AC,BC,并分别取线段AC,BC的中点E,F,测得,则______m.
19.(2022春·福建福州·八年级统考期末)菱形两条对角线长为8cm和6cm,则菱形面积为_______cm2.
20.(2022春·福建厦门·八年级统考期末)如图,四边形是菱形,,,于点,则________.
三、解答题
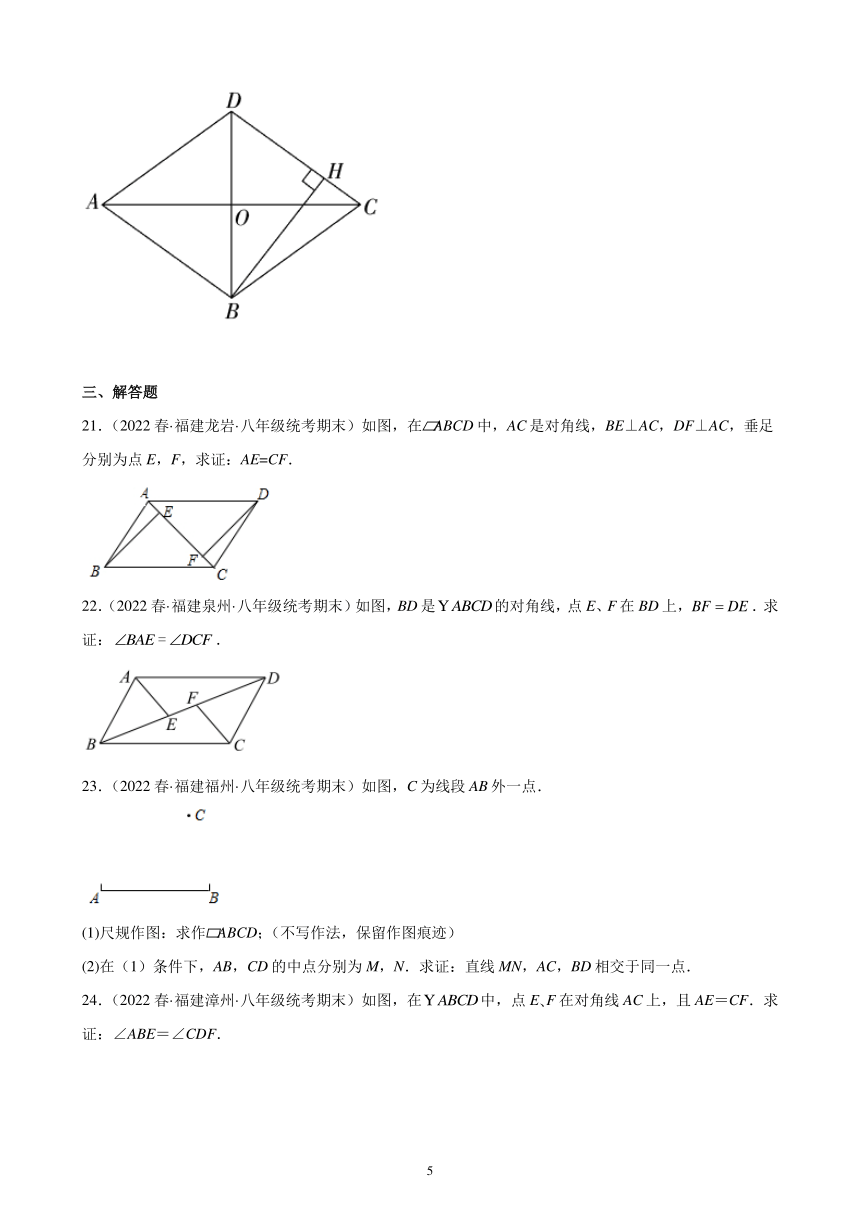
21.(2022春·福建龙岩·八年级统考期末)如图,在 ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为点E,F,求证:AE=CF.
22.(2022春·福建泉州·八年级统考期末)如图,BD是的对角线,点E、F在BD上,.求证:.
23.(2022春·福建福州·八年级统考期末)如图,C为线段AB外一点.
(1)尺规作图:求作 ABCD;(不写作法,保留作图痕迹)
(2)在(1)条件下,AB,CD的中点分别为M,N.求证:直线MN,AC,BD相交于同一点.
24.(2022春·福建漳州·八年级统考期末)如图,在中,点E F在对角线AC上,且AE=CF.求证:∠ABE=∠CDF.
25.(2022春·福建福州·八年级统考期末)已知:如图,在平行四边形ABDC中,点E、F在AD上,且AE=DF,
求证:四边形BECF是平行四边形.
26.(2022春·福建厦门·八年级期末)如图1,四边形中,AB//DC,.
(1)求证:四边形是平行四边形;
(2)如图2,过点D作的垂线,垂足为E,过点B作的垂线,垂足为F,连接,若,求证:;
(3)如图3,在(2)的条件下,在线段上取一点P,连接,交于T若,求的长.
27.(2022春·福建泉州·八年级统考期末)如图,在矩形ABCD中,连接BD,将绕点A逆时针旋转90°得,其中D、B的对应点分别是P、E,连接CP.
(1)若,求证:四边形PBDC为平行四边形;
(2)延长DB交PE于F,连接FA.
①若,,求FB的长;
②求证:.
28.(2022春·福建漳州·八年级统考期末)【性质探究】
(1)如图1,在△ABC中,点D E分别是边AB AC的中点,连接DE.
求证:,.
【类比应用】
(2)如图2,将△ABC绕点A逆时针旋转90°得到△ADE,连接CD BE,点F为BE的中点,连接AF,若AF=3,求CD的长.
29.(2022春·福建福州·八年级统考期末)已知:如图,点E,F分别在的AB,DC边上,且,连接DE,BF.求证:四边形DEBF是平行四边形.
30.(2022春·福建厦门·八年级统考期末)如图,在△ABC中,∠ABC=60°,AB=2,BC=4.
(1)求作直线AE,使得AEBC;(要求:尺规作图,不写作法,保留作图痕迹)
(2)D是直线AE上一点,AC与BD交于点O,且OB=OD,求四边形ABCD的面积.
31.(2022春·福建龙岩·八年级统考期末)已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
32.(2022春·福建泉州·八年级统考期末)如图,在 ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF,求证:四边形AECF是菱形.
33.(2022春·福建泉州·八年级统考期末)已知正方形ABCD的边长等于4,点E为边AD上一动点,连接CE,以CE为边长作正方形CEFG(点D、F在CE所在直线的同侧),H为CD中点,连接FH.
(1)如图1,当点E为AD中点时,连接BE,BH,求证:四边形BEFH为菱形;
(2)如图2,连接EH,若,求的面积;
(3)在点E的运动过程中,求AF的最小值.
34.(2022春·福建三明·八年级统考期末)已知,如图①,在中,,,AC的垂直平分线分别交AD,AC,BC于点E,O,F,连接AF,CE.
(1)求证:;
(2)如图②,动点P,Q分别从A,C两点同时出发,沿和各边匀速运动一周.即点P自停止,点Q自停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当点P运动到FB上,点Q运动到DE上,且四边形APCQ是平行四边形时,求t的值;
②设点P,Q的运动路程分别为a,b,当四边形APCQ是平行四边形时,求a与b满足的数量关系式.
35.(2022春·福建福州·八年级统考期末)如图,正方形,点E,F是对角线上的两点,,连接,,和关于直线对称.点G在上,连接.
(1)求的度数;
(2)如备用图,延长交于点H.连接
①求证:四边形是菱形;
②求的值.
36.(2022春·福建泉州·八年级统考期末)如图,已知正方形ABCD中,,CE与DF的交点为O.求证:.
参考答案:
1.D
【分析】确定有关平行四边形,关键是确定平行四边形的四个顶点,由此即可解决问题.
【详解】只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故选D.
【点睛】本题考查平行四边形的定义以及性质,解题的关键是理解如何确定平行四边形的四个顶点,四个顶点的位置确定了,平行四边形的大小就确定了,属于中考常考题型.
2.C
【分析】根据平行四边形的性质,即可求解.
【详解】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠A=∠EBC=50°,∠A+∠D=180°,
∴∠D=130°.
故选:C
【点睛】本题主要考查了平行四边形的性质,熟练掌握平行四边形的性质是解题的关键.
3.C
【分析】由平行四边形的判定分别对各个选项进行判断即可.
【详解】解:A、由ABCD,AD=BC,不能判定四边形ABCD为平行四边形,故选项A不符合题意;
B、由∠A=∠B,∠C=∠D,不能判定四边形ABCD为平行四边形,故选项B不符合题意;
C、∵AB=CD,AD=BC,
∴四边形ABCD为平行四边形,故选项C符合题意;
D、由AB=AD,CB=CD,不能判定四边形ABCD为平行四边形,故选项D不符合题意;
故选:C.
【点睛】本题考查了平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键.
4.B
【分析】根据平行四边形的判定定理(①两组对角分别相等的四边形是平行四边形,②两组对边分别相等的四边形是平行四边形,③对角线互相平分的四边形是平行四边形,④有一组对边相等且平行的四边形是平行四边形)进行判断即可.
【详解】解:A、错误.一组对边平行无法判断四边形是平行四边形;
B、正确.对角线互相平分的四边形是平行四边形;
C、错误.一组对角相等无法判断四边形是平行四边形;
D、错误.对角线互相平分的四边形才是平行四边形,而对角线互相垂直的四边形不一定是平行四边形
【点睛】本题考查了对平行四边形的判定定理,熟记平行四边形的判定方法是解决问题的关键.
5.B
【分析】作出图形,根据三角形的中位线定理可得EF=GH=AC,FG=EH=BD,即可得解.
【详解】解:如图,连接AC、BD,
∵E、F、G、H分别是的AB、BC、CD、AD边上的中点,
∴EF=GH=AC,FG=EH=BD(三角形的中位线等于第三边的一半),
∴四边形EFGH是平行四边形.
故选:B.
【点睛】本题考查了中点四边形,三角形的中位线定理,作辅助线构造出三角形,然后利用三角形的中位线定理是解题的关键.
6.D
【分析】过点P作,构造平行四边形和直角三角形,利用平行四边形的性质和直角三角形的性质及勾股定理求解.
【详解】解:如图,过点P作,
,, OP平分∠AOB,
,,
四边形是平行四边形,
,
,
,
,
,
,
,
,,
点P的坐标是,
故选:D.
【点睛】本题考查平行四边形和直角三角形的知识,涉及知识点:平行四边形的性质与判定,三角形外角的性质,直角三角形中所对直角边等于斜边的一半,勾股定理,解题关键构造平行四边形和直角三角形.
7.C
【分析】延长CM交AD于N,先由AAS证得△BCM≌△DNM,得出NM=CM=CN,DN=BC=3,求出AN=BC,得出四边形ABCN是平行四边形,即可得出结果.
【详解】解:延长CM交AD于N,如图所示:
∵点M是线段BD的中点,
∴BM=DM,
∵ADBC,
∴∠CBM=∠NDM,∠BCM=∠DNM,
在△BCM和△DNM中,
,
∴△BCM≌△DNM(AAS),
∴NM=CM=CN,DN=BC=3,
∴AN=AD﹣DN=6﹣3=3,
∴AN=BC,
∵ADBC,
∴四边形ABCN是平行四边形,
∴CN=AB=5,
∴CM=,
故选:C.
【点睛】本题考查了全等三角形的判定与性质、平行线的性质、平行四边形的判定与性质等知识,添加辅助线证明△BCM≌△DNM是解题的关键.
8.A
【分析】根据三角形中位线定理解答即可.
【详解】解:∵E,F分别为AC,BC中点,
∴EF是△ABC的中位线,
∴EF=AB=×6=3,
故选:A.
【点睛】本题考查了三角形中位线定理.三角形的中位线平行于第三边,且等于第三边的一半.
9.B
【分析】利用三角形中位线定理得到DE∥AC,结合平行四边形的判定定理对各个选项进行判断即可.
【详解】解:∵D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC,
A.根据∠B=∠F不能判定CF∥AB,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
B.∵∠B=∠BCF,
∴CF∥AB,即CF∥AD,
∴四边形ADFC为平行四边形,故本选项符合题意;
C.根据AC=CF不能判定CF∥AB,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项不符合题意;
故选:B.
【点睛】本题考查了平行四边形的判定、三角形的中位线定理以及平行线的判定等知识;熟练掌握平行四边形的判定和三角形中位线定理是解题的关键.
10.D
【分析】根据矩形的判定定理判定即可.
【详解】A.测量两组对边是否相等,能判定平行四边形,故A错误;
B.对角线相等的四边形不一定是矩形,不能判定四边形的形状,故B错误;
C.测量对角线是否互相平分,能判定平行四边形,故C错误;
D.根据对角线相等且互相平分四边形是矩形,可知量出对角线的交点到四个顶点的距离,看是否相等,可判断是否是矩形.故D正确.
故选:D.
【点睛】本题主要考查了矩形的判定定理,矩形的判定定理有:(1)有一个角是直角的平行四边形是矩形;(2)有三个角是直角的四边形是矩形;(3)对角线互相平分且相等的四边形是矩形.
11.C
【分析】根据矩形的性质得到OA=OB=OD,结合得到,进一步得到BD=2AB.
【详解】因为四边形为矩形,
所以,
,
,
所以,
所以,
因为
所以
因为,
所以,
故.
故选C.
【点睛】本题考查了矩形的性质和含的直角三角形的边角关系,本题也可用等边三角形的性质和矩形的性质进行求解.
12.B
【分析】连接BP,则PC+QD的最小值转化为PC+PB的最小值,在BA的延长线上截取AE=AB=4,连接PE、CE,则PC+QD=PC+PB=PC+PE≥CE,再根据勾股定理求解即可.
【详解】解:如图,连接BP,
在矩形ABCD中,AD∥BC,AD=BC=6,
∵AP=CQ,
∴AD-AP=BC-CQ,
∴DP=QB,DP∥BQ,
∴四边形DPBQ是平行四边形,
∴PB∥DQ,PB=DQ,
则PC+QD=PC+PB,则PC+QD的最小值转化为PC+PB的最小值,
在BA的延长线上截取AE=AB=4,连接PE,CE,
则BE=2AB=8,
∵PA⊥BE,
∴PA是BE的垂直平分线,
∴PB=PE,
∴PC+PB=PC+PE,
连接CE,则PC+QD=PC+PB=PC+PE≥CE,
∴CE==10,
∴PC+PB的最小值为10,
即PC+QD的最小值为10,
故选:B.
【点睛】本题考查的是矩形的性质、平行四边形的判定与性质、勾股定理等知识;熟练掌握矩形的性质和平行四边形的判定与性质,证出PC+QD=PC+PB=PC+PE≥CE是解题的关键.
13.C
【分析】根据正方形、等边三角形和三角形内角和定理可以得到答案.
【详解】四边形是正方形,
,,
是等边三角形,
,,
,,
,
故选:C.
【点睛】本题考查正方形、等边三角形和三角形内角和定理的综合应用,灵活运用有关性质求解是解题关键.
14.3
【分析】先证明CB=CF,再结合平行四边形的性质,计算即可.
【详解】因为四边形ABCD是平行四边形,
所以BC=AD,ABCF,AB=CD,
所以∠ABF=∠BFC,
因为BF平分∠ABC,
所以∠ABF=∠CBF,
所以∠BFC=∠CBF,
所以CB=CF,
因为CF=CD+DF,
所以AD=AB+DF,
所以AB=7-4=3(cm),
故答案为:3.
【点睛】本题考查了平行四边形的性质,角的平分线的意义,熟练掌握平行四边形的性质是解题的关键.
15.①③④
【分析】根据平行四边形的性质及全等三角形的判定和性质可判断①;结合图形可判断②;利用平行四边形的性质及全等三角形的判定和性质,对顶角的性质可判断③;利用平行四边形的性质及三角形的面积公式可判断④.
【详解】解:∵平行四边形ABCD中,E是BD的中点,
∴BE=DE,AD∥BC,AD=BC,
∴∠MDE=∠NBE,∠DME=∠BNE,
∴ DME BNE,
∴DM=BN,
∴AM=CN,故①正确;
由图可得:BM>AB≠AD=BC,
故②错误;
连接AE、CE,
四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∵平行四边形ABCD中,E是BD的中点,
∴BE=DE,
∴ ADE CBE,
∴AE=CE,∠AED=∠CEB,
点A、E、C三点共线,故③正确;
如图所示:过点D、E两点向BC作垂线分别为Q和P点,
∵E是BD的中点,且点E为平行四边形对角线的交点,
∴DQ=2EP,
,
,
∴,故④正确;
故答案为:①③④.
【点睛】题目主要考查平行四边形的性质,全等三角形的判定和性质等,理解题意综合运用这些知识点是解题关键.
16.②③
【分析】由于符合题目的已知条件的除了平行四边形之外,还有等腰梯形,故①错误;因为两组对角分别相等的四边形是平行四边形,所以②正确;根据,可得,又由于,可判定,再依据平行四边形的定义可得结论;过点作于,在上截取,连接,根据线段垂直平分线性质可得出
,将绕点顺时针旋转,使与重合,得到,再结合平行四边形的性质,可证出,,这样的四边形满足题目已知条件,但不符合命题的结论,不是平行四边形,所以④错误,这样就可得解.
【详解】①因为一组对边平行,另一组对边相等可以是平行四边形,也可以是等腰梯形,所以①错误;
②因为两组对角分别相等的四边形是平行四边形,所以②正确;
③∵
∴
∵
∴
∴
∴四边形是平行四边形
因此③正确;
④作,连接,
过点作于,在上截取,连接,
∵,,
∴,
将绕点顺时针旋转,使与重合,得到,
由作图可知:,,
∵四边形是平行四边形,
∴,,
∴,,
显然,图中的四边形不是平行四边形.
所以④错误;
故答案为:②③.
【点睛】本题主要考查了平行四边形的性质与判定,旋转的性质与作图,熟练掌握平行四边形的性质与判定是解本题的关键,同时要注意真命题需要证明,假命题只需举出反例即可.
17.2
【分析】首先过点C作CE∥AD交AB于点E,可得四边形ADCE是平行四边形,继而可证得△BCE是等腰三角形,则可求得答案.
【详解】过点C作CE∥AD交AB于点E,
∵AB∥CD,
∴四边形ADCE是平行四边形,
∴AE=CD,CE=AD=3,∠CEA=∠D=2∠B,
∵∠CEA=∠B+∠BCE,
∴∠B=∠BCE,
∴BE=CE=3,
∴CD=AE=AB BE=5 3=2
故答案为:2
【点睛】本题考查了平行四边形的判定与性质,等腰三角形的性质.
18.12
【分析】利用三角形中位线定理求解即可.
【详解】解:∵E、F分别是AC,BC的中点,
∴EF是△ABC的中位线,
∴AB=2EF=12m,
故答案为:12.
【点睛】本题主要考查了三角形中位线定理,熟知三角形中位线定理是解题的关键.
19.24
【分析】根据菱形的面积等于两对角线乘积的一半求其面积即可.
【详解】解:菱形面积是6×8÷2=24cm2;
故答案为24.
【点睛】本题考查的是菱形的面积的计算,掌握“菱形的面积等于两条对角线乘积的一半”是解本题的关键.
20.
【分析】首先根据菱形的性质,得出,的长,然后再根据勾股定理,得出的长,再利用菱形的面积,即可得出的长.
【详解】解:∵四边形是菱形,
∴,,
又∵,
∴,
∴,
∵,
∴,
解得:.
故答案为:
【点睛】本题主要考查了菱形的性质,勾股定理,解本题的关键在于能够熟练掌握菱形的性质.
21.证明见解析.
【分析】由全等三角形的判定定理AAS证得△ABE≌△CDF,则对应边相等:AE=CF.
【详解】如图,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF.
又BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°.
在△ABE与△CDF中,
,
∴得△ABE≌△CDF(AAS),
∴AE=CF.
【点睛】本题考查了全等三角形的判定与性质,熟练掌握三角形全等的判定方法并准确识图是解题的关键.
22.见解析
【分析】根据平行四边形的性质得,则可得∠ABE=∠CDF,利用可证得,根据全等三角形的性质即可求证结论.
【详解】证明:∵BF=DE
∴BF-EF=DE-EF,
∴BE=DF,
∵四边形ABCD是平行四边形,
∴,
∴∠ABE=∠CDF,
在和中,
,
∴,
∴.
【点睛】本题考查了平行四边形的性质、全等三角形的判定及性质,熟练掌握全等三角形的判定及性质是解题的关键.
23.(1)见解析
(2)见解析
【分析】(1)连接BC,再分别以A点、C点为圆心,以BC、AB为半径画弧,两弧相交于点D,则四边形ABCD满足条件;
(2)设AC与BD相交于点O,连接CM、AN,如图,利用平行四边形的性质得到OA=OC,CD∥AB,AB=CD,再证明四边形AMCN为平行四边形,则MN与AC互相平分,从而可判断直线MN,AC,BD相交于同一点.
(1)
解:如图,平行四边形为所作;
(2)
证明:设与相交于点O,连接,如图,
∵四边形为平行四边形,
∴,
∵点M为的中点,点N为的中点,
∴,
即,
∴四边形为平行四边形,
∴与互相平分,即过的中点O,
∴直线相交于同一点.
【点睛】本题考查了作图——复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行四边形的判定与性质.
24.见解析
【分析】根据平行四边形的性质得到AB∥CD,AB=CD,推出∠BAC=∠DCA,即可证明△ABE≌△CDF,由此得到结论.
【详解】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAC=∠DCA,
又AE=CF,
∴△ABE≌△CDF,
∴∠ABE=∠CDF.
【点睛】此题考查了平行四边形的性质,全等三角形的判定及性质,正确理解并掌握各性质定理是解题的关键.
25.证明见解析.
【分析】根据平行四边形的性质,可得对角线互相平分,根据对角线互相平分的四边形是平行四边形,可得证明结论.
【详解】解:如图,连接BC,设对角线交于点O.
∵四边形ABDC是平行四边形,
∴OA=OD,OB=OC.
∵AE=DF,
∴OA﹣AE=OD﹣DF,
∴OE=OF.
∴四边形BECF是平行四边形.
26.(1)见解析
(2)见解析
(3)9
【分析】(1)利用平行线的判定和性质,只要证得即可;
(2)利用直角三角形的两锐角互余,结合已知,可证得,,进而利用等角对等边即可求证;
(3)延长EF交CD延长线于M,延长FE交CP延长线于H,通过导角证明三角形MHC和三角形EHP都是等腰三角形,进而求出AE,再利用即可求出AB,从而得到的长.
(1)
证明:∵,
∴,
∵,
∴,
∴,
∴四边形是平行四边形;
(2)
证明:∵,
∴,,
∵,
∴,
又∵,
∴,
∴,,
∴,,
∴;
(3)
解:如图,延长EF交CD延长线于M,延长FE交CP延长线于H.
∵ AB//DC,
∴,
在和中,
,
∴,
∴,,.
∵,由(1)知,
∴ ,
∴ .
由(1)知,
设,
∴.
,
,
∵,,
,
,
,
又∵,
,
,
,
,
∵,
∴,
∴,
∴,
,
设,,
则,
,
,
解得,
即,
由勾股定理可得,,
,
∵,
,
解得,
,
即CD的长为9.
【点睛】本题考查平行四边形的判定与性质,全等三角形的判定与性质,等腰三角形的判定与性质,勾股定理解直角三角形等,第三问难度较大,通过导角证明三角形MHC和三角形EHP是等腰三角形是解题的关键.
27.(1)见解析
(2)①;②见解析
【分析】(1)根据旋转性质得出PA=AD,从而可得PA=2AB,进而得出PB=CD,然后根据“一组对边平行且相等的四边形是平行四边形”即可得证;
(2)①先在Rt△ABD中求出AB=2,进而求出,然后判断△PFB为直角三角形,∠FPB=30°,最后根据“含30度的直角三角形的性质”求解即可;
②过点A作AM⊥EF于M,AN⊥DF于N,过点B作BH⊥AF于H,过点E作于G,先证,得出AN=AM,进而可证∠EFA=∠BFA=45°,即可求出, ,然后证明,得出,最后代入化简即可得证.
(1)
证明:矩形ABCD中,,AB=CD,
∵AD=2AB,AD=PA,
∴PB=PA-AB=AB,
∴PB=CD,
又∵,
∴四边形PBDC为平行四边形;
(2)
①解:由旋转性质得,
∴,
在中,设AB=x,则BD=2AB=2x,
∵,
∴
∴x=2,
∴AB=2,
∴,
∵∠BAD=90°,∠ADB=30°,
∴∠ABD=60°
∴∠
∵∠PFB是的外角
∴
在中,
∴
②:过点A作AM⊥EF于M,AN⊥DF于N,过点B作BH⊥AF于H,过点E作于G,
∴∠AMF=90°,∠ANF=90°,
∴∠AMF=∠AND,
又∵AD=AP,∠ADN=∠APM
∴,
∴AN=AM,
又∵AM⊥EF,AN⊥DF,
∴AF平分∠EFD,
∵∠PFB=90°,
∴,
∴∠EFA=∠BFA=45°
∵BH⊥AF,EG⊥FA,
∴中,
中,.
∵,
∴
∵,
∴,
∴
∵,
∴
即
【点睛】本题考查了矩形的性质,旋转的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质等知识,添加合适的辅助线是解题的关键.
28.(1)见解析;(2)6
【分析】(1)利用“边角边”证明△ADE和△CEF全等,根据全等三角形对应边相等可得AD=CF,然后判断出四边形BCFD是平行四边形,根据平行四边形的性质可得;
(2)延长BA至点G,使AG=AB,连接GE,利用“边角边”证明△ACD≌△AEG,根据全等三角形对应边相等可得CD=GE,由点A F分别是边BG BE的中点,得出,求出CD的长.
【详解】解:(1)证明:延长DE至点F,使EF=DE,连接CF,
∵点E是AC的中点,
∴AE=CE.
又∠AED=∠CEF,
∴△AED≌△CEF,
∴AD=CF,∠ADE=∠CFE,
∴AB∥CF,即.
∵点D是边AB的中点,
∴AD=DB,
∴DB=CF,
∴四边形BCFD是平行四边形,
∴,DF=BC.
∴.
又,
∴.
(2)延长BA至点G,使AG=AB,连接GE,
∵将△ABC绕点A逆时针旋转90°得到△ADE,
∴∠BAD=∠CAE=90°,AC=AE,AD=AB,
∴∠DAG=90°,AD=AG.
又∠CAD=90°-∠DAE=∠EAG,
∴△ACD≌△AEG,
∴CD=GE.
∵点A F分别是边BG BE的中点,
∴
∴.
又AF=3,
∴CD=6.
【点睛】此题主要考查了平行四边形的性质和判定,全等三角形的判定和性质,判断三角形全等是解决本题的关键.
29.见解析
【分析】由平行四边形的性质得出,再根据已知条件得出,即可得出结论.
【详解】四边形ABCD是平行四边形,
,
,
,
四边形DEBF是平行四边形.
【点睛】本题考查了平行四边形的性质和判定,熟练掌握知识点是解题的关键.
30.(1)见解析
(2)
【分析】(1)过A点作∠BAE=∠B,可得AEBC;
(2)根据题意作出图形,过A点作AF⊥BC于F,根据含30°角的直角三角形的性质求出BF,再根据勾股定理求出AF,可得四边形ABCD是平行四边形,再根据平行四边形的面积公式计算即可求解.
(1)
解:如图所示,AE即为所求.
(2)
解:如图,
∵AEBC,
∴∠DAC=∠BCA.
∵∠DOA=∠BOC,OB=OD,
∴△AOD≌△BOC.
∴AD=BC.(或OA=OC)
∴四边形ABCD是平行四边形.
过点A作AF⊥BC于点F,
∴∠AFC=90°.
∵∠ABC=60°,AB=2,
∴BF=1,AF=
∵BC=4,
∴四边形ABCD的面积为BC·AF=4.
【点睛】本题考查了复杂作图,勾股定理,直角三角形的性质,关键是会作一条直线的平行线.
31.(1)证明见解析;(2)结论:四边形ACDF是矩形.理由见解析
【分析】(1)只要证明AB=CD,AF=CD即可解决问题;
(2)结论:四边形ACDF是矩形.根据对角线相等的平行四边形是矩形判断即可;
【详解】解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠AFC=∠DCG,
∵GA=GD,∠AGF=∠CGD,
∴△AGF≌△DGC,
∴AF=CD,
∴AB=AF.
(2)解:结论:四边形ACDF是矩形.
理由:∵AF=CD,AF∥CD,
∴四边形ACDF是平行四边形,
∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD=120°,
∴∠FAG=60°,
∵AB=AG=AF,
∴△AFG是等边三角形,
∴AG=GF,
∵△AGF≌△DGC,
∴FG=CG,∵AG=GD,
∴AD=CF,
∴四边形ACDF是矩形.
【点睛】本题考查平行四边形的判定和性质、矩形的判定、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.
32.见解析
【分析】根据对角线互相垂直的平行四边形是菱形即可证明
【详解】证明:四边形是平行四边形,
,,
,
,,
四边形是平行四边形,
,
四边形是菱形.
【点睛】本题考查平行四边形的性质、菱形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
33.(1)见解析
(2)
(3)AF的最小值是
【分析】(1)先证,推出,,再结合正方形的性质得出,,得出四边形BEFH为平行四边形,再由得出,即可证明四边形BEFH为菱形;
(2)连接EH,连接DF,过点F作,交AD延长线于点M,利用求解;
(3)连接AF,先证,设,则,,由勾股定理得,可知当,即点E与点A重合时,AF有最小值.
【详解】(1)证明: 四边形ABCD是正方形,
,.
又E为AD中点,H为CD中点,
,
在与中,
,
.
,.
,
,
,
在正方形CEFG中,,,
,,
四边形BEFH为平行四边形.
同理可证,
,
四边形BEFH为菱形;
(2)解:如图,连接EH,连接DF,过点F作,交AD延长线于点M,
,
.
,,
,
在与中,
,
,
,,
,
;
(3)解:如图,连接AF,
由(2)可知,,
,,
,
,
设,则,,
在中,由勾股定理,得.
当,即点E与点A重合时,AF有最小值.
【点睛】本题考查全等三角形的判定与性质,菱形的判定,正方形的性质,三角形面积公式以及勾股定理解直角三角形,综合性较强,有一定难度,综合运用上述知识点、正确作出辅助线是解题的关键.
34.(1)见解析
(2)①;②
【分析】(1)首先证明,由此得出,从而证明四边形为菱形即可证明结论;
(2)①设菱形AFCE的边长,分别求出,,,,即可得到,由此求解即可;②根据题意分当点在上、点在上时或当点在上、点在上时以及当点在上、点在上时三种情况进一步分析求解即可.
(1)
解:∵四边形是矩形,
∴,
∴,.
∵垂直平分,垂足为,
∴,
在和△COF中,
∵
∴,
∴,
∴四边形为平行四边形,
又∵,
∴四边形为菱形,
∴AE=CF;
(2)
解:①设菱形AFCE的边长,
∵四边形APCQ是平行四边形,
∴PC=AQ,
∵四边形ABCD是平行四边形,
∴CD=AB=4cm,AD=BC=8cm,
∵点的速度为每秒,点的速度为每秒,运动时间为秒,
∴,,
∴,,
∴,
解得:,
②由题意得,当四边形APCQ是平行四边形时,点、在互相平行的对应边上,
设,
分三种情况:
其一:如图1,当点在上、点在上时,
∵,
∴,
∴;
其二:如图2,当点在上、点在上时,
∴,
∴,
∴,
∴;
其三:如图3,当点在上、点在上时,
∴,
∵,,
∴,
∴,
综上所述,a与b满足的数量关系式为.
【点睛】本题主要考查了菱形的判定、全等三角形性质及判定、平行四边形的动点问题,熟练掌握相关知识是解题关键.
35.(1)
(2)①见解析;②
【分析】(1)设对角线的交点为O,根据可得出,再根据和关于直线对称,可知,从而可得出答案;
(2)①利用SAS可证明,,可得出,,再根据正方形的性质得出,可以推出、,即可得出四边形GHCF为平行四边形,再根据即可得证;
②根据①中的结论易证△DGH为等腰直角三角形,可得出,再根据菱形的性质及线段的和即可得出,从而得出答案.
(1)
解:设对角线的交点为O
和关于直线对称
(2)
①和关于直线对称
四边形ABCD为正方形
,
四边形GHCF为平行四边形
四边形GHCF为菱形;
②由①知
△DGH为等腰直角三角形
四边形GHCF为菱形
.
【点睛】本题考查了正方形的性质,菱形的判定及性质,对称图形的性质,等腰三角形的判定及性质,全等三角形的判定及性质,勾股定理,综合性较强,熟练掌握性质定理是解题的关键.
36.见解析
【分析】利用直角三角形全等的判定得出,并由全等三角形的性质得出,最后根据直角三角形的两锐角互余和垂直定义证明结论.
【详解】证明:正方形ABCD中,,,
,
(HL).
.
,
.
DF与CE相交于点O,
.
.
【点睛】本题考查正方形的性质,全等三角形的性质与判定的理解与综合运用能力.主要涉及正方形四个边相等,四个角都为;斜边和一条直角边分别相等的两个直角三角形全等(HL);全等三角形的对应边相等,对应角相、直角三角形的两锐角互余等知识点.灵活运用正方形的性质,直角三角形全等的判定是解本题的关键.
一、单选题
1.(2022春·福建龙岩·八年级统考期末)小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
A.①,② B.①,④ C.③,④ D.②,③
2.(2022春·福建宁德·八年级统考期末)如图,四边形ABCD是平行四边形,E是AB延长线上一点,若∠EBC=50°,则∠D的度数为( )
A.50° B.100° C.130° D.150°
3.(2022春·福建龙岩·八年级统考期末)下列给出的条件能判定四边形为平行四边形的是( )
A.AB//CD, B.,
C., D.,
4.(2022春·福建福州·八年级统考期末)下列条件中,能判定四边形是平行四边形的是( )
A.一组对边平行 B.对角线互相平分
C.一组对边相等 D.对角线互相垂直
5.(2022春·福建福州·八年级统考期末)若顺次连接平行四边形各边中点所得四边形必定是( )
A.矩形 B.平行四边形 C.正方形 D.菱形
6.(2022春·福建南平·八年级统考期末)如图,在平面直角坐标系中,□AOBC的顶点B在x轴上,OA=2,∠AOB =60°, OP平分∠AOB交AC边于点P,则点P的坐标是是( )
A. B.
C. D.
7.(2022春·福建泉州·八年级统考期末)如图,四边形中,ADBC,,,.若点是线段的中点,则的长为( )
A. B.2 C. D.3
8.(2022春·福建福州·八年级统考期末)如图,在△ABC中,E,F分别为AC,BC中点,若AB=6,BC=7,AC=8,则EF=( )
A.3 B.3.5 C.4 D.4.5
9.(2022春·福建厦门·八年级统考期末)如图,在中,D,E分别是的中点,点F在延长线上,添加一个条件使四边形为平行四边形,则这个条件是( )
A. B. C. D.
10.(2022春·福建福州·八年级统考期末)要判断一个四边形的窗框是否为矩形,可行的测量方案是( )
A.测量两组对边是否相等
B.测量对角线是否相等
C.测量对角线是否互相平分
D.测量对角线交点到四个顶点的距离是否都相等
11.(2022春·福建泉州·八年级统考期末)如图,矩形的两条对角线相交于点,已知,,则矩形对角线的长为( )
A. B. C. D.
12.(2022春·福建福州·八年级统考期末)如图,在矩形ABCD中,AB=4,AD=6,点P在AD上,点Q在BC上,且AP = CQ,连接CP,QD,则PC + QD的最小值为( )
A.8 B.10 C.12 D.20
13.(2022春·福建南平·八年级统考期末)如图,正方形ABCD外侧作等边三角形ADE,则∠AEB的度数为( )
A.30° B.20° C.15° D.10°
二、填空题
14.(2022春·福建龙岩·八年级统考期末)如图,在平行四边形ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=_____cm.
15.(2022春·福建泉州·八年级统考期末)如图,在中,E点是BD的中点,MN经过E点分别与AD、BC相交于点M、N.下列四个结论:
①;②;③A、C、E三点共线;④若,则.其中正确的结论有____.(写出所有正确结论的序号)
16.(2022春·福建漳州·八年级统考期末)在四边形中,现给出下列结论:
①若,,则四边形是平行四边形;
②若,,则四边形是平行四边形;
③若,,则四边形是平行四边形;
④若,,则四边形是平行四边形.
其中正确的结论是____________.(写出所有正确结论的序号)
17.(2022春·福建泉州·八年级统考期末)如图,在四边形ABCD中,AB∥CD,∠D=2∠B,若AD=3,AB=5,则CD=______.
18.(2022春·福建三明·八年级统考期末)如图,A,B两处被池塘隔开,为了测量A,B两处的距离,在AB外选一适当的点C,连接AC,BC,并分别取线段AC,BC的中点E,F,测得,则______m.
19.(2022春·福建福州·八年级统考期末)菱形两条对角线长为8cm和6cm,则菱形面积为_______cm2.
20.(2022春·福建厦门·八年级统考期末)如图,四边形是菱形,,,于点,则________.
三、解答题
21.(2022春·福建龙岩·八年级统考期末)如图,在 ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为点E,F,求证:AE=CF.
22.(2022春·福建泉州·八年级统考期末)如图,BD是的对角线,点E、F在BD上,.求证:.
23.(2022春·福建福州·八年级统考期末)如图,C为线段AB外一点.
(1)尺规作图:求作 ABCD;(不写作法,保留作图痕迹)
(2)在(1)条件下,AB,CD的中点分别为M,N.求证:直线MN,AC,BD相交于同一点.
24.(2022春·福建漳州·八年级统考期末)如图,在中,点E F在对角线AC上,且AE=CF.求证:∠ABE=∠CDF.
25.(2022春·福建福州·八年级统考期末)已知:如图,在平行四边形ABDC中,点E、F在AD上,且AE=DF,
求证:四边形BECF是平行四边形.
26.(2022春·福建厦门·八年级期末)如图1,四边形中,AB//DC,.
(1)求证:四边形是平行四边形;
(2)如图2,过点D作的垂线,垂足为E,过点B作的垂线,垂足为F,连接,若,求证:;
(3)如图3,在(2)的条件下,在线段上取一点P,连接,交于T若,求的长.
27.(2022春·福建泉州·八年级统考期末)如图,在矩形ABCD中,连接BD,将绕点A逆时针旋转90°得,其中D、B的对应点分别是P、E,连接CP.
(1)若,求证:四边形PBDC为平行四边形;
(2)延长DB交PE于F,连接FA.
①若,,求FB的长;
②求证:.
28.(2022春·福建漳州·八年级统考期末)【性质探究】
(1)如图1,在△ABC中,点D E分别是边AB AC的中点,连接DE.
求证:,.
【类比应用】
(2)如图2,将△ABC绕点A逆时针旋转90°得到△ADE,连接CD BE,点F为BE的中点,连接AF,若AF=3,求CD的长.
29.(2022春·福建福州·八年级统考期末)已知:如图,点E,F分别在的AB,DC边上,且,连接DE,BF.求证:四边形DEBF是平行四边形.
30.(2022春·福建厦门·八年级统考期末)如图,在△ABC中,∠ABC=60°,AB=2,BC=4.
(1)求作直线AE,使得AEBC;(要求:尺规作图,不写作法,保留作图痕迹)
(2)D是直线AE上一点,AC与BD交于点O,且OB=OD,求四边形ABCD的面积.
31.(2022春·福建龙岩·八年级统考期末)已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
32.(2022春·福建泉州·八年级统考期末)如图,在 ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF,求证:四边形AECF是菱形.
33.(2022春·福建泉州·八年级统考期末)已知正方形ABCD的边长等于4,点E为边AD上一动点,连接CE,以CE为边长作正方形CEFG(点D、F在CE所在直线的同侧),H为CD中点,连接FH.
(1)如图1,当点E为AD中点时,连接BE,BH,求证:四边形BEFH为菱形;
(2)如图2,连接EH,若,求的面积;
(3)在点E的运动过程中,求AF的最小值.
34.(2022春·福建三明·八年级统考期末)已知,如图①,在中,,,AC的垂直平分线分别交AD,AC,BC于点E,O,F,连接AF,CE.
(1)求证:;
(2)如图②,动点P,Q分别从A,C两点同时出发,沿和各边匀速运动一周.即点P自停止,点Q自停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当点P运动到FB上,点Q运动到DE上,且四边形APCQ是平行四边形时,求t的值;
②设点P,Q的运动路程分别为a,b,当四边形APCQ是平行四边形时,求a与b满足的数量关系式.
35.(2022春·福建福州·八年级统考期末)如图,正方形,点E,F是对角线上的两点,,连接,,和关于直线对称.点G在上,连接.
(1)求的度数;
(2)如备用图,延长交于点H.连接
①求证:四边形是菱形;
②求的值.
36.(2022春·福建泉州·八年级统考期末)如图,已知正方形ABCD中,,CE与DF的交点为O.求证:.
参考答案:
1.D
【分析】确定有关平行四边形,关键是确定平行四边形的四个顶点,由此即可解决问题.
【详解】只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故选D.
【点睛】本题考查平行四边形的定义以及性质,解题的关键是理解如何确定平行四边形的四个顶点,四个顶点的位置确定了,平行四边形的大小就确定了,属于中考常考题型.
2.C
【分析】根据平行四边形的性质,即可求解.
【详解】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠A=∠EBC=50°,∠A+∠D=180°,
∴∠D=130°.
故选:C
【点睛】本题主要考查了平行四边形的性质,熟练掌握平行四边形的性质是解题的关键.
3.C
【分析】由平行四边形的判定分别对各个选项进行判断即可.
【详解】解:A、由ABCD,AD=BC,不能判定四边形ABCD为平行四边形,故选项A不符合题意;
B、由∠A=∠B,∠C=∠D,不能判定四边形ABCD为平行四边形,故选项B不符合题意;
C、∵AB=CD,AD=BC,
∴四边形ABCD为平行四边形,故选项C符合题意;
D、由AB=AD,CB=CD,不能判定四边形ABCD为平行四边形,故选项D不符合题意;
故选:C.
【点睛】本题考查了平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键.
4.B
【分析】根据平行四边形的判定定理(①两组对角分别相等的四边形是平行四边形,②两组对边分别相等的四边形是平行四边形,③对角线互相平分的四边形是平行四边形,④有一组对边相等且平行的四边形是平行四边形)进行判断即可.
【详解】解:A、错误.一组对边平行无法判断四边形是平行四边形;
B、正确.对角线互相平分的四边形是平行四边形;
C、错误.一组对角相等无法判断四边形是平行四边形;
D、错误.对角线互相平分的四边形才是平行四边形,而对角线互相垂直的四边形不一定是平行四边形
【点睛】本题考查了对平行四边形的判定定理,熟记平行四边形的判定方法是解决问题的关键.
5.B
【分析】作出图形,根据三角形的中位线定理可得EF=GH=AC,FG=EH=BD,即可得解.
【详解】解:如图,连接AC、BD,
∵E、F、G、H分别是的AB、BC、CD、AD边上的中点,
∴EF=GH=AC,FG=EH=BD(三角形的中位线等于第三边的一半),
∴四边形EFGH是平行四边形.
故选:B.
【点睛】本题考查了中点四边形,三角形的中位线定理,作辅助线构造出三角形,然后利用三角形的中位线定理是解题的关键.
6.D
【分析】过点P作,构造平行四边形和直角三角形,利用平行四边形的性质和直角三角形的性质及勾股定理求解.
【详解】解:如图,过点P作,
,, OP平分∠AOB,
,,
四边形是平行四边形,
,
,
,
,
,
,
,
,,
点P的坐标是,
故选:D.
【点睛】本题考查平行四边形和直角三角形的知识,涉及知识点:平行四边形的性质与判定,三角形外角的性质,直角三角形中所对直角边等于斜边的一半,勾股定理,解题关键构造平行四边形和直角三角形.
7.C
【分析】延长CM交AD于N,先由AAS证得△BCM≌△DNM,得出NM=CM=CN,DN=BC=3,求出AN=BC,得出四边形ABCN是平行四边形,即可得出结果.
【详解】解:延长CM交AD于N,如图所示:
∵点M是线段BD的中点,
∴BM=DM,
∵ADBC,
∴∠CBM=∠NDM,∠BCM=∠DNM,
在△BCM和△DNM中,
,
∴△BCM≌△DNM(AAS),
∴NM=CM=CN,DN=BC=3,
∴AN=AD﹣DN=6﹣3=3,
∴AN=BC,
∵ADBC,
∴四边形ABCN是平行四边形,
∴CN=AB=5,
∴CM=,
故选:C.
【点睛】本题考查了全等三角形的判定与性质、平行线的性质、平行四边形的判定与性质等知识,添加辅助线证明△BCM≌△DNM是解题的关键.
8.A
【分析】根据三角形中位线定理解答即可.
【详解】解:∵E,F分别为AC,BC中点,
∴EF是△ABC的中位线,
∴EF=AB=×6=3,
故选:A.
【点睛】本题考查了三角形中位线定理.三角形的中位线平行于第三边,且等于第三边的一半.
9.B
【分析】利用三角形中位线定理得到DE∥AC,结合平行四边形的判定定理对各个选项进行判断即可.
【详解】解:∵D,E分别是AB,BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC,
A.根据∠B=∠F不能判定CF∥AB,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
B.∵∠B=∠BCF,
∴CF∥AB,即CF∥AD,
∴四边形ADFC为平行四边形,故本选项符合题意;
C.根据AC=CF不能判定CF∥AB,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;
D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项不符合题意;
故选:B.
【点睛】本题考查了平行四边形的判定、三角形的中位线定理以及平行线的判定等知识;熟练掌握平行四边形的判定和三角形中位线定理是解题的关键.
10.D
【分析】根据矩形的判定定理判定即可.
【详解】A.测量两组对边是否相等,能判定平行四边形,故A错误;
B.对角线相等的四边形不一定是矩形,不能判定四边形的形状,故B错误;
C.测量对角线是否互相平分,能判定平行四边形,故C错误;
D.根据对角线相等且互相平分四边形是矩形,可知量出对角线的交点到四个顶点的距离,看是否相等,可判断是否是矩形.故D正确.
故选:D.
【点睛】本题主要考查了矩形的判定定理,矩形的判定定理有:(1)有一个角是直角的平行四边形是矩形;(2)有三个角是直角的四边形是矩形;(3)对角线互相平分且相等的四边形是矩形.
11.C
【分析】根据矩形的性质得到OA=OB=OD,结合得到,进一步得到BD=2AB.
【详解】因为四边形为矩形,
所以,
,
,
所以,
所以,
因为
所以
因为,
所以,
故.
故选C.
【点睛】本题考查了矩形的性质和含的直角三角形的边角关系,本题也可用等边三角形的性质和矩形的性质进行求解.
12.B
【分析】连接BP,则PC+QD的最小值转化为PC+PB的最小值,在BA的延长线上截取AE=AB=4,连接PE、CE,则PC+QD=PC+PB=PC+PE≥CE,再根据勾股定理求解即可.
【详解】解:如图,连接BP,
在矩形ABCD中,AD∥BC,AD=BC=6,
∵AP=CQ,
∴AD-AP=BC-CQ,
∴DP=QB,DP∥BQ,
∴四边形DPBQ是平行四边形,
∴PB∥DQ,PB=DQ,
则PC+QD=PC+PB,则PC+QD的最小值转化为PC+PB的最小值,
在BA的延长线上截取AE=AB=4,连接PE,CE,
则BE=2AB=8,
∵PA⊥BE,
∴PA是BE的垂直平分线,
∴PB=PE,
∴PC+PB=PC+PE,
连接CE,则PC+QD=PC+PB=PC+PE≥CE,
∴CE==10,
∴PC+PB的最小值为10,
即PC+QD的最小值为10,
故选:B.
【点睛】本题考查的是矩形的性质、平行四边形的判定与性质、勾股定理等知识;熟练掌握矩形的性质和平行四边形的判定与性质,证出PC+QD=PC+PB=PC+PE≥CE是解题的关键.
13.C
【分析】根据正方形、等边三角形和三角形内角和定理可以得到答案.
【详解】四边形是正方形,
,,
是等边三角形,
,,
,,
,
故选:C.
【点睛】本题考查正方形、等边三角形和三角形内角和定理的综合应用,灵活运用有关性质求解是解题关键.
14.3
【分析】先证明CB=CF,再结合平行四边形的性质,计算即可.
【详解】因为四边形ABCD是平行四边形,
所以BC=AD,ABCF,AB=CD,
所以∠ABF=∠BFC,
因为BF平分∠ABC,
所以∠ABF=∠CBF,
所以∠BFC=∠CBF,
所以CB=CF,
因为CF=CD+DF,
所以AD=AB+DF,
所以AB=7-4=3(cm),
故答案为:3.
【点睛】本题考查了平行四边形的性质,角的平分线的意义,熟练掌握平行四边形的性质是解题的关键.
15.①③④
【分析】根据平行四边形的性质及全等三角形的判定和性质可判断①;结合图形可判断②;利用平行四边形的性质及全等三角形的判定和性质,对顶角的性质可判断③;利用平行四边形的性质及三角形的面积公式可判断④.
【详解】解:∵平行四边形ABCD中,E是BD的中点,
∴BE=DE,AD∥BC,AD=BC,
∴∠MDE=∠NBE,∠DME=∠BNE,
∴ DME BNE,
∴DM=BN,
∴AM=CN,故①正确;
由图可得:BM>AB≠AD=BC,
故②错误;
连接AE、CE,
四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
∵平行四边形ABCD中,E是BD的中点,
∴BE=DE,
∴ ADE CBE,
∴AE=CE,∠AED=∠CEB,
点A、E、C三点共线,故③正确;
如图所示:过点D、E两点向BC作垂线分别为Q和P点,
∵E是BD的中点,且点E为平行四边形对角线的交点,
∴DQ=2EP,
,
,
∴,故④正确;
故答案为:①③④.
【点睛】题目主要考查平行四边形的性质,全等三角形的判定和性质等,理解题意综合运用这些知识点是解题关键.
16.②③
【分析】由于符合题目的已知条件的除了平行四边形之外,还有等腰梯形,故①错误;因为两组对角分别相等的四边形是平行四边形,所以②正确;根据,可得,又由于,可判定,再依据平行四边形的定义可得结论;过点作于,在上截取,连接,根据线段垂直平分线性质可得出
,将绕点顺时针旋转,使与重合,得到,再结合平行四边形的性质,可证出,,这样的四边形满足题目已知条件,但不符合命题的结论,不是平行四边形,所以④错误,这样就可得解.
【详解】①因为一组对边平行,另一组对边相等可以是平行四边形,也可以是等腰梯形,所以①错误;
②因为两组对角分别相等的四边形是平行四边形,所以②正确;
③∵
∴
∵
∴
∴
∴四边形是平行四边形
因此③正确;
④作,连接,
过点作于,在上截取,连接,
∵,,
∴,
将绕点顺时针旋转,使与重合,得到,
由作图可知:,,
∵四边形是平行四边形,
∴,,
∴,,
显然,图中的四边形不是平行四边形.
所以④错误;
故答案为:②③.
【点睛】本题主要考查了平行四边形的性质与判定,旋转的性质与作图,熟练掌握平行四边形的性质与判定是解本题的关键,同时要注意真命题需要证明,假命题只需举出反例即可.
17.2
【分析】首先过点C作CE∥AD交AB于点E,可得四边形ADCE是平行四边形,继而可证得△BCE是等腰三角形,则可求得答案.
【详解】过点C作CE∥AD交AB于点E,
∵AB∥CD,
∴四边形ADCE是平行四边形,
∴AE=CD,CE=AD=3,∠CEA=∠D=2∠B,
∵∠CEA=∠B+∠BCE,
∴∠B=∠BCE,
∴BE=CE=3,
∴CD=AE=AB BE=5 3=2
故答案为:2
【点睛】本题考查了平行四边形的判定与性质,等腰三角形的性质.
18.12
【分析】利用三角形中位线定理求解即可.
【详解】解:∵E、F分别是AC,BC的中点,
∴EF是△ABC的中位线,
∴AB=2EF=12m,
故答案为:12.
【点睛】本题主要考查了三角形中位线定理,熟知三角形中位线定理是解题的关键.
19.24
【分析】根据菱形的面积等于两对角线乘积的一半求其面积即可.
【详解】解:菱形面积是6×8÷2=24cm2;
故答案为24.
【点睛】本题考查的是菱形的面积的计算,掌握“菱形的面积等于两条对角线乘积的一半”是解本题的关键.
20.
【分析】首先根据菱形的性质,得出,的长,然后再根据勾股定理,得出的长,再利用菱形的面积,即可得出的长.
【详解】解:∵四边形是菱形,
∴,,
又∵,
∴,
∴,
∵,
∴,
解得:.
故答案为:
【点睛】本题主要考查了菱形的性质,勾股定理,解本题的关键在于能够熟练掌握菱形的性质.
21.证明见解析.
【分析】由全等三角形的判定定理AAS证得△ABE≌△CDF,则对应边相等:AE=CF.
【详解】如图,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF.
又BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°.
在△ABE与△CDF中,
,
∴得△ABE≌△CDF(AAS),
∴AE=CF.
【点睛】本题考查了全等三角形的判定与性质,熟练掌握三角形全等的判定方法并准确识图是解题的关键.
22.见解析
【分析】根据平行四边形的性质得,则可得∠ABE=∠CDF,利用可证得,根据全等三角形的性质即可求证结论.
【详解】证明:∵BF=DE
∴BF-EF=DE-EF,
∴BE=DF,
∵四边形ABCD是平行四边形,
∴,
∴∠ABE=∠CDF,
在和中,
,
∴,
∴.
【点睛】本题考查了平行四边形的性质、全等三角形的判定及性质,熟练掌握全等三角形的判定及性质是解题的关键.
23.(1)见解析
(2)见解析
【分析】(1)连接BC,再分别以A点、C点为圆心,以BC、AB为半径画弧,两弧相交于点D,则四边形ABCD满足条件;
(2)设AC与BD相交于点O,连接CM、AN,如图,利用平行四边形的性质得到OA=OC,CD∥AB,AB=CD,再证明四边形AMCN为平行四边形,则MN与AC互相平分,从而可判断直线MN,AC,BD相交于同一点.
(1)
解:如图,平行四边形为所作;
(2)
证明:设与相交于点O,连接,如图,
∵四边形为平行四边形,
∴,
∵点M为的中点,点N为的中点,
∴,
即,
∴四边形为平行四边形,
∴与互相平分,即过的中点O,
∴直线相交于同一点.
【点睛】本题考查了作图——复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行四边形的判定与性质.
24.见解析
【分析】根据平行四边形的性质得到AB∥CD,AB=CD,推出∠BAC=∠DCA,即可证明△ABE≌△CDF,由此得到结论.
【详解】证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAC=∠DCA,
又AE=CF,
∴△ABE≌△CDF,
∴∠ABE=∠CDF.
【点睛】此题考查了平行四边形的性质,全等三角形的判定及性质,正确理解并掌握各性质定理是解题的关键.
25.证明见解析.
【分析】根据平行四边形的性质,可得对角线互相平分,根据对角线互相平分的四边形是平行四边形,可得证明结论.
【详解】解:如图,连接BC,设对角线交于点O.
∵四边形ABDC是平行四边形,
∴OA=OD,OB=OC.
∵AE=DF,
∴OA﹣AE=OD﹣DF,
∴OE=OF.
∴四边形BECF是平行四边形.
26.(1)见解析
(2)见解析
(3)9
【分析】(1)利用平行线的判定和性质,只要证得即可;
(2)利用直角三角形的两锐角互余,结合已知,可证得,,进而利用等角对等边即可求证;
(3)延长EF交CD延长线于M,延长FE交CP延长线于H,通过导角证明三角形MHC和三角形EHP都是等腰三角形,进而求出AE,再利用即可求出AB,从而得到的长.
(1)
证明:∵,
∴,
∵,
∴,
∴,
∴四边形是平行四边形;
(2)
证明:∵,
∴,,
∵,
∴,
又∵,
∴,
∴,,
∴,,
∴;
(3)
解:如图,延长EF交CD延长线于M,延长FE交CP延长线于H.
∵ AB//DC,
∴,
在和中,
,
∴,
∴,,.
∵,由(1)知,
∴ ,
∴ .
由(1)知,
设,
∴.
,
,
∵,,
,
,
,
又∵,
,
,
,
,
∵,
∴,
∴,
∴,
,
设,,
则,
,
,
解得,
即,
由勾股定理可得,,
,
∵,
,
解得,
,
即CD的长为9.
【点睛】本题考查平行四边形的判定与性质,全等三角形的判定与性质,等腰三角形的判定与性质,勾股定理解直角三角形等,第三问难度较大,通过导角证明三角形MHC和三角形EHP是等腰三角形是解题的关键.
27.(1)见解析
(2)①;②见解析
【分析】(1)根据旋转性质得出PA=AD,从而可得PA=2AB,进而得出PB=CD,然后根据“一组对边平行且相等的四边形是平行四边形”即可得证;
(2)①先在Rt△ABD中求出AB=2,进而求出,然后判断△PFB为直角三角形,∠FPB=30°,最后根据“含30度的直角三角形的性质”求解即可;
②过点A作AM⊥EF于M,AN⊥DF于N,过点B作BH⊥AF于H,过点E作于G,先证,得出AN=AM,进而可证∠EFA=∠BFA=45°,即可求出, ,然后证明,得出,最后代入化简即可得证.
(1)
证明:矩形ABCD中,,AB=CD,
∵AD=2AB,AD=PA,
∴PB=PA-AB=AB,
∴PB=CD,
又∵,
∴四边形PBDC为平行四边形;
(2)
①解:由旋转性质得,
∴,
在中,设AB=x,则BD=2AB=2x,
∵,
∴
∴x=2,
∴AB=2,
∴,
∵∠BAD=90°,∠ADB=30°,
∴∠ABD=60°
∴∠
∵∠PFB是的外角
∴
在中,
∴
②:过点A作AM⊥EF于M,AN⊥DF于N,过点B作BH⊥AF于H,过点E作于G,
∴∠AMF=90°,∠ANF=90°,
∴∠AMF=∠AND,
又∵AD=AP,∠ADN=∠APM
∴,
∴AN=AM,
又∵AM⊥EF,AN⊥DF,
∴AF平分∠EFD,
∵∠PFB=90°,
∴,
∴∠EFA=∠BFA=45°
∵BH⊥AF,EG⊥FA,
∴中,
中,.
∵,
∴
∵,
∴,
∴
∵,
∴
即
【点睛】本题考查了矩形的性质,旋转的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质等知识,添加合适的辅助线是解题的关键.
28.(1)见解析;(2)6
【分析】(1)利用“边角边”证明△ADE和△CEF全等,根据全等三角形对应边相等可得AD=CF,然后判断出四边形BCFD是平行四边形,根据平行四边形的性质可得;
(2)延长BA至点G,使AG=AB,连接GE,利用“边角边”证明△ACD≌△AEG,根据全等三角形对应边相等可得CD=GE,由点A F分别是边BG BE的中点,得出,求出CD的长.
【详解】解:(1)证明:延长DE至点F,使EF=DE,连接CF,
∵点E是AC的中点,
∴AE=CE.
又∠AED=∠CEF,
∴△AED≌△CEF,
∴AD=CF,∠ADE=∠CFE,
∴AB∥CF,即.
∵点D是边AB的中点,
∴AD=DB,
∴DB=CF,
∴四边形BCFD是平行四边形,
∴,DF=BC.
∴.
又,
∴.
(2)延长BA至点G,使AG=AB,连接GE,
∵将△ABC绕点A逆时针旋转90°得到△ADE,
∴∠BAD=∠CAE=90°,AC=AE,AD=AB,
∴∠DAG=90°,AD=AG.
又∠CAD=90°-∠DAE=∠EAG,
∴△ACD≌△AEG,
∴CD=GE.
∵点A F分别是边BG BE的中点,
∴
∴.
又AF=3,
∴CD=6.
【点睛】此题主要考查了平行四边形的性质和判定,全等三角形的判定和性质,判断三角形全等是解决本题的关键.
29.见解析
【分析】由平行四边形的性质得出,再根据已知条件得出,即可得出结论.
【详解】四边形ABCD是平行四边形,
,
,
,
四边形DEBF是平行四边形.
【点睛】本题考查了平行四边形的性质和判定,熟练掌握知识点是解题的关键.
30.(1)见解析
(2)
【分析】(1)过A点作∠BAE=∠B,可得AEBC;
(2)根据题意作出图形,过A点作AF⊥BC于F,根据含30°角的直角三角形的性质求出BF,再根据勾股定理求出AF,可得四边形ABCD是平行四边形,再根据平行四边形的面积公式计算即可求解.
(1)
解:如图所示,AE即为所求.
(2)
解:如图,
∵AEBC,
∴∠DAC=∠BCA.
∵∠DOA=∠BOC,OB=OD,
∴△AOD≌△BOC.
∴AD=BC.(或OA=OC)
∴四边形ABCD是平行四边形.
过点A作AF⊥BC于点F,
∴∠AFC=90°.
∵∠ABC=60°,AB=2,
∴BF=1,AF=
∵BC=4,
∴四边形ABCD的面积为BC·AF=4.
【点睛】本题考查了复杂作图,勾股定理,直角三角形的性质,关键是会作一条直线的平行线.
31.(1)证明见解析;(2)结论:四边形ACDF是矩形.理由见解析
【分析】(1)只要证明AB=CD,AF=CD即可解决问题;
(2)结论:四边形ACDF是矩形.根据对角线相等的平行四边形是矩形判断即可;
【详解】解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠AFC=∠DCG,
∵GA=GD,∠AGF=∠CGD,
∴△AGF≌△DGC,
∴AF=CD,
∴AB=AF.
(2)解:结论:四边形ACDF是矩形.
理由:∵AF=CD,AF∥CD,
∴四边形ACDF是平行四边形,
∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD=120°,
∴∠FAG=60°,
∵AB=AG=AF,
∴△AFG是等边三角形,
∴AG=GF,
∵△AGF≌△DGC,
∴FG=CG,∵AG=GD,
∴AD=CF,
∴四边形ACDF是矩形.
【点睛】本题考查平行四边形的判定和性质、矩形的判定、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.
32.见解析
【分析】根据对角线互相垂直的平行四边形是菱形即可证明
【详解】证明:四边形是平行四边形,
,,
,
,,
四边形是平行四边形,
,
四边形是菱形.
【点睛】本题考查平行四边形的性质、菱形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
33.(1)见解析
(2)
(3)AF的最小值是
【分析】(1)先证,推出,,再结合正方形的性质得出,,得出四边形BEFH为平行四边形,再由得出,即可证明四边形BEFH为菱形;
(2)连接EH,连接DF,过点F作,交AD延长线于点M,利用求解;
(3)连接AF,先证,设,则,,由勾股定理得,可知当,即点E与点A重合时,AF有最小值.
【详解】(1)证明: 四边形ABCD是正方形,
,.
又E为AD中点,H为CD中点,
,
在与中,
,
.
,.
,
,
,
在正方形CEFG中,,,
,,
四边形BEFH为平行四边形.
同理可证,
,
四边形BEFH为菱形;
(2)解:如图,连接EH,连接DF,过点F作,交AD延长线于点M,
,
.
,,
,
在与中,
,
,
,,
,
;
(3)解:如图,连接AF,
由(2)可知,,
,,
,
,
设,则,,
在中,由勾股定理,得.
当,即点E与点A重合时,AF有最小值.
【点睛】本题考查全等三角形的判定与性质,菱形的判定,正方形的性质,三角形面积公式以及勾股定理解直角三角形,综合性较强,有一定难度,综合运用上述知识点、正确作出辅助线是解题的关键.
34.(1)见解析
(2)①;②
【分析】(1)首先证明,由此得出,从而证明四边形为菱形即可证明结论;
(2)①设菱形AFCE的边长,分别求出,,,,即可得到,由此求解即可;②根据题意分当点在上、点在上时或当点在上、点在上时以及当点在上、点在上时三种情况进一步分析求解即可.
(1)
解:∵四边形是矩形,
∴,
∴,.
∵垂直平分,垂足为,
∴,
在和△COF中,
∵
∴,
∴,
∴四边形为平行四边形,
又∵,
∴四边形为菱形,
∴AE=CF;
(2)
解:①设菱形AFCE的边长,
∵四边形APCQ是平行四边形,
∴PC=AQ,
∵四边形ABCD是平行四边形,
∴CD=AB=4cm,AD=BC=8cm,
∵点的速度为每秒,点的速度为每秒,运动时间为秒,
∴,,
∴,,
∴,
解得:,
②由题意得,当四边形APCQ是平行四边形时,点、在互相平行的对应边上,
设,
分三种情况:
其一:如图1,当点在上、点在上时,
∵,
∴,
∴;
其二:如图2,当点在上、点在上时,
∴,
∴,
∴,
∴;
其三:如图3,当点在上、点在上时,
∴,
∵,,
∴,
∴,
综上所述,a与b满足的数量关系式为.
【点睛】本题主要考查了菱形的判定、全等三角形性质及判定、平行四边形的动点问题,熟练掌握相关知识是解题关键.
35.(1)
(2)①见解析;②
【分析】(1)设对角线的交点为O,根据可得出,再根据和关于直线对称,可知,从而可得出答案;
(2)①利用SAS可证明,,可得出,,再根据正方形的性质得出,可以推出、,即可得出四边形GHCF为平行四边形,再根据即可得证;
②根据①中的结论易证△DGH为等腰直角三角形,可得出,再根据菱形的性质及线段的和即可得出,从而得出答案.
(1)
解:设对角线的交点为O
和关于直线对称
(2)
①和关于直线对称
四边形ABCD为正方形
,
四边形GHCF为平行四边形
四边形GHCF为菱形;
②由①知
△DGH为等腰直角三角形
四边形GHCF为菱形
.
【点睛】本题考查了正方形的性质,菱形的判定及性质,对称图形的性质,等腰三角形的判定及性质,全等三角形的判定及性质,勾股定理,综合性较强,熟练掌握性质定理是解题的关键.
36.见解析
【分析】利用直角三角形全等的判定得出,并由全等三角形的性质得出,最后根据直角三角形的两锐角互余和垂直定义证明结论.
【详解】证明:正方形ABCD中,,,
,
(HL).
.
,
.
DF与CE相交于点O,
.
.
【点睛】本题考查正方形的性质,全等三角形的性质与判定的理解与综合运用能力.主要涉及正方形四个边相等,四个角都为;斜边和一条直角边分别相等的两个直角三角形全等(HL);全等三角形的对应边相等,对应角相、直角三角形的两锐角互余等知识点.灵活运用正方形的性质,直角三角形全等的判定是解本题的关键.
