2022-2023学年冀教版九年级数学下册29.2直线与圆的位置关系专题练习(无答案)
文档属性
| 名称 | 2022-2023学年冀教版九年级数学下册29.2直线与圆的位置关系专题练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 266.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-18 00:00:00 | ||
图片预览


文档简介
29.2直线与圆的位置关系专题练习
班级:________ 姓名:________
一、单选题(共 8 小题)
1、圆的半径为5cm,圆心与直线上某一点的距离为5cm,则直线与圆的位置关系是( )
A.相离 B.相切 C.相交或相切 D.相离或相切
2、圆的直径是8cm,若圆心与直线的距离是4cm,则该直线和圆的位置关系是( )
A.相离 B.相切 C.相交 D.相交或相切
3、如图,已知直线与x轴,y轴分别交于A,B两点,P是以C(0,2)为圆心,2为半径的圆上一动点,连接PA,PB,则面积的最大值是( )
A.62 B.42 C.52 D.50
4、已知圆心到两直线、的距离,分别是方程的两根,且,⊙O的半径为3,则直线、与的位置关系分别为( )
A.相离、相交 B.相切、相交 C.相离、相切 D.相交、相离
5、⊙O的半径是3,点O到直线l的距离是5,则直线l与⊙O的位置关系是( )
A.相切 B.相交 C.相离 D.以上都不对
6、⊙O的半径为R,直线l与⊙O有公共点,如果圆心到直线l的距离为d,那么d与R的大小关系是( )
A. B. C. D.
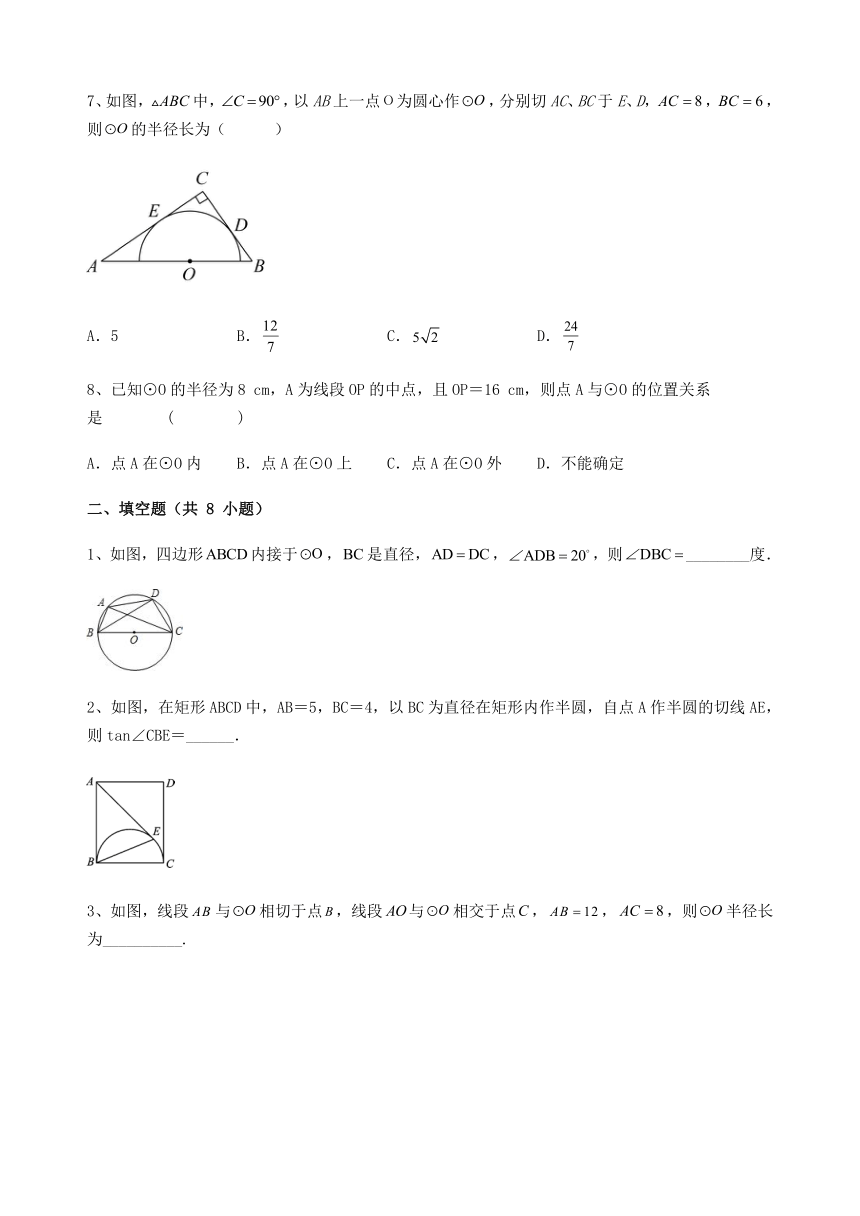
7、如图,中,,以AB上一点О为圆心作,分别切AC、BC于E、D,,,则的半径长为( )
A.5 B. C. D.
8、已知⊙O的半径为8 cm,A为线段OP的中点,且OP=16 cm,则点A与⊙O的位置关系是 ( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
二、填空题(共 8 小题)
1、如图,四边形内接于,是直径,,,则________度.
2、如图,在矩形ABCD中,AB=5,BC=4,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则tan∠CBE=______.
3、如图,线段与相切于点,线段与相交于点,,,则半径长为__________.
4、在平面直角坐标系中,以点A(﹣2,3)为圆心、r为半径的圆与坐标轴恰好有三个公共点,那么r的值为_____.
5、如图,在中,,,,,分别是、的中点,则以为直径的圆与的位置关系是__________.
6、如图,交于点,,,的半径为5,则的长为________.
7、如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=4 cm,以点C为圆心,以3 cm长为半径作圆,则⊙C与AB的位置关系是_____
8、若⊙O的半径为4cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系是________.
三、解答题(共 5 小题)
1、已知:及边上一点.
求作:,使与边相切,点为切点,且圆心到两边的距离相等.
2、如图,已知.请用尺规作的外接圆⊙O.(保留作图痕迹,不写作法)
3、如图所示,AB是ABC外接圆⊙O的直径,过⊙O外一点D作BC的平行线分别交AC,AB于点G,E,交⊙O于点F,连接DB,CF,∠BAC=∠D.
(1)求证:BD是⊙O的切线;
(2)若点E是OA的中点,CF平分∠ACB,设BD=18,求DE的长.
4、如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D, 点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E、F.
(1)试判断直线BC与OD的位置关系,并说明理由.
(2)若BD=,BF=3,求⊙O的半径.
5、如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若AB=12,sinA=0.6,求△BDE的边BE上的高.
班级:________ 姓名:________
一、单选题(共 8 小题)
1、圆的半径为5cm,圆心与直线上某一点的距离为5cm,则直线与圆的位置关系是( )
A.相离 B.相切 C.相交或相切 D.相离或相切
2、圆的直径是8cm,若圆心与直线的距离是4cm,则该直线和圆的位置关系是( )
A.相离 B.相切 C.相交 D.相交或相切
3、如图,已知直线与x轴,y轴分别交于A,B两点,P是以C(0,2)为圆心,2为半径的圆上一动点,连接PA,PB,则面积的最大值是( )
A.62 B.42 C.52 D.50
4、已知圆心到两直线、的距离,分别是方程的两根,且,⊙O的半径为3,则直线、与的位置关系分别为( )
A.相离、相交 B.相切、相交 C.相离、相切 D.相交、相离
5、⊙O的半径是3,点O到直线l的距离是5,则直线l与⊙O的位置关系是( )
A.相切 B.相交 C.相离 D.以上都不对
6、⊙O的半径为R,直线l与⊙O有公共点,如果圆心到直线l的距离为d,那么d与R的大小关系是( )
A. B. C. D.
7、如图,中,,以AB上一点О为圆心作,分别切AC、BC于E、D,,,则的半径长为( )
A.5 B. C. D.
8、已知⊙O的半径为8 cm,A为线段OP的中点,且OP=16 cm,则点A与⊙O的位置关系是 ( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
二、填空题(共 8 小题)
1、如图,四边形内接于,是直径,,,则________度.
2、如图,在矩形ABCD中,AB=5,BC=4,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则tan∠CBE=______.
3、如图,线段与相切于点,线段与相交于点,,,则半径长为__________.
4、在平面直角坐标系中,以点A(﹣2,3)为圆心、r为半径的圆与坐标轴恰好有三个公共点,那么r的值为_____.
5、如图,在中,,,,,分别是、的中点,则以为直径的圆与的位置关系是__________.
6、如图,交于点,,,的半径为5,则的长为________.
7、如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=4 cm,以点C为圆心,以3 cm长为半径作圆,则⊙C与AB的位置关系是_____
8、若⊙O的半径为4cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系是________.
三、解答题(共 5 小题)
1、已知:及边上一点.
求作:,使与边相切,点为切点,且圆心到两边的距离相等.
2、如图,已知.请用尺规作的外接圆⊙O.(保留作图痕迹,不写作法)
3、如图所示,AB是ABC外接圆⊙O的直径,过⊙O外一点D作BC的平行线分别交AC,AB于点G,E,交⊙O于点F,连接DB,CF,∠BAC=∠D.
(1)求证:BD是⊙O的切线;
(2)若点E是OA的中点,CF平分∠ACB,设BD=18,求DE的长.
4、如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D, 点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E、F.
(1)试判断直线BC与OD的位置关系,并说明理由.
(2)若BD=,BF=3,求⊙O的半径.
5、如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若AB=12,sinA=0.6,求△BDE的边BE上的高.
