2022-2023学年华东师大版八年级数学下册17.5实践与探索课后综合练习(无答案)
文档属性
| 名称 | 2022-2023学年华东师大版八年级数学下册17.5实践与探索课后综合练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 360.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-18 12:08:36 | ||
图片预览



文档简介
17.5实践与探索课后综合练习
班级:________ 姓名:________
一、单选题(共 8 小题)
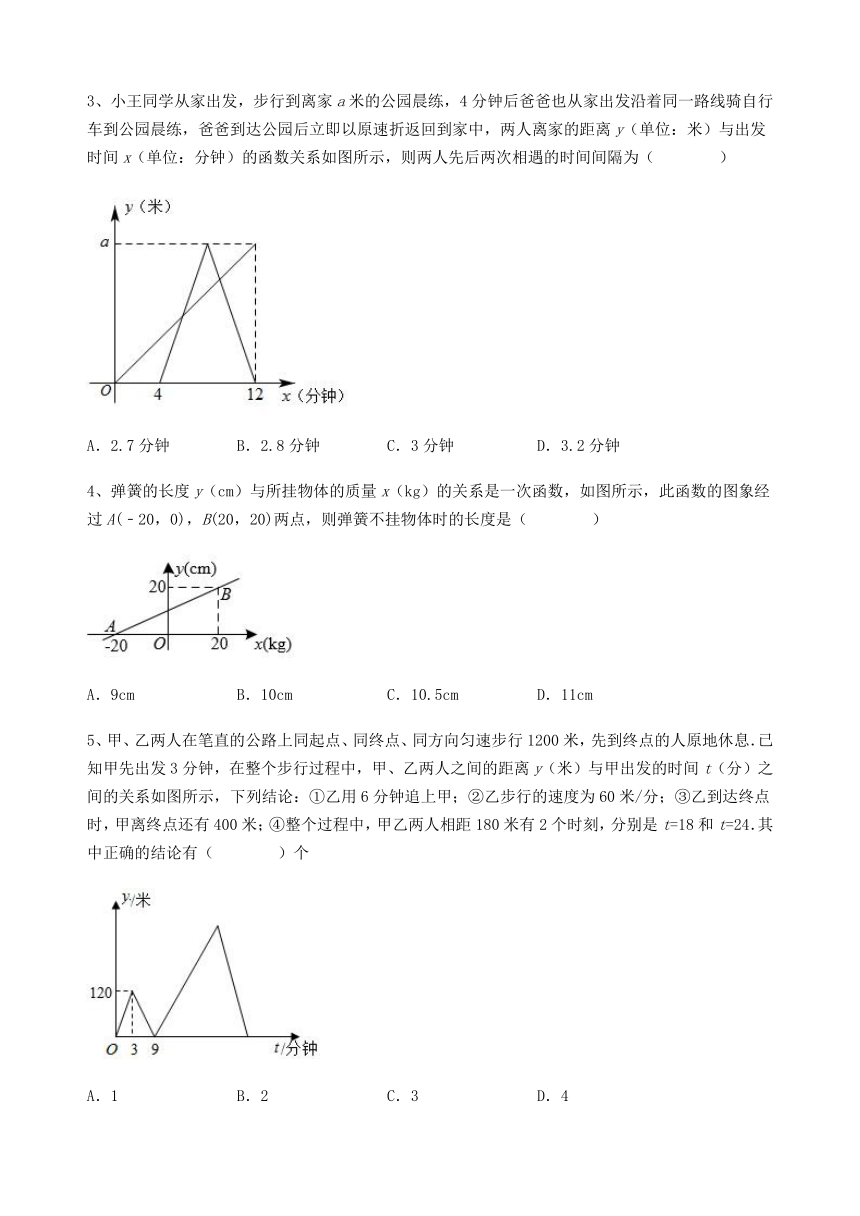
1、某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)与该校参加竞赛人数的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( )
A.甲 B.乙 C.丙 D.丁
2、如图,已知直线与坐标轴分别交于、两点,那么过原点且将的面积平分的直线的解析式为( )
A. B. C. D.
3、小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
A.2.7分钟 B.2.8分钟 C.3分钟 D.3.2分钟
4、弹簧的长度y(cm)与所挂物体的质量x(kg)的关系是一次函数,如图所示,此函数的图象经过A(﹣20,0),B(20,20)两点,则弹簧不挂物体时的长度是( )
A.9cm B.10cm C.10.5cm D.11cm
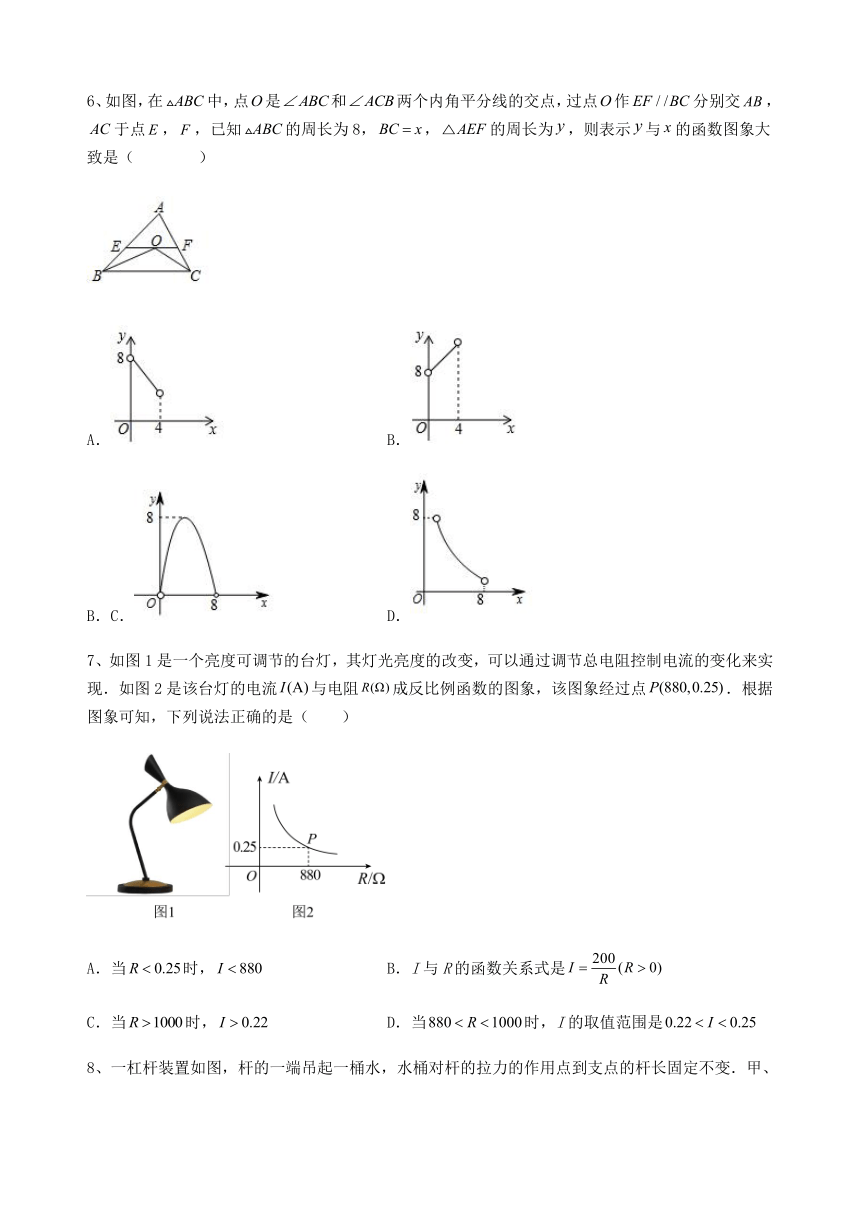
5、甲、乙两人在笔直的公路上同起点、同终点、同方向匀速步行1200米,先到终点的人原地休息.已知甲先出发3分钟,在整个步行过程中,甲、乙两人之间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①乙用6分钟追上甲;②乙步行的速度为60米/分;③乙到达终点时,甲离终点还有400米;④整个过程中,甲乙两人相距180米有2个时刻,分别是t=18和t=24.其中正确的结论有( )个
A.1 B.2 C.3 D.4
6、如图,在中,点是和两个内角平分线的交点,过点作分别交,于点,,已知的周长为8,,的周长为,则表示与的函数图象大致是( )
B.
C. D.
7、如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流与电阻成反比例函数的图象,该图象经过点.根据图象可知,下列说法正确的是( )
A.当时, B.I与R的函数关系式是
C.当时, D.当时,I的取值范围是
8、一杠杆装置如图,杆的一端吊起一桶水,水桶对杆的拉力的作用点到支点的杆长固定不变.甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力、、、,将相同重量的水桶吊起同样的高度,若,则这四位同学对杆的压力的作用点到支点的距离最远的是( )
A.甲同学 B.乙同学 C.丙同学 D.丁同学
二、填空题(共 6 小题)
1、已知点A在反比例函数的图象上,点B在x轴正半轴上,若为等腰三角形,且腰长为5,则的长为__________.
2、、两地在一条笔直的公路上,甲从地出发前往地、乙从地出发前往地,两人同时出发,甲到达地后停止,乙继续前进到达地,如图表示两人的距离(米与时间(分间的函数关系,则下列结论中:①、两地的距离是1200米;②两人出发4分钟相遇;③甲的速度是100米分;④乙出发12分钟到达地,正确的有 __(填序号)
3、甲、乙两名同学参加户外拓展活动,过程如下:甲、乙分别从直线赛道、两端同时出发,匀速相向而行.相遇时,甲将出发时在地抽取的任务单递给乙后继续向地前行,乙就原地执行任务,用时14分钟,再继续向地前行,此时甲尚未到达地.当甲和乙分别到达地和地后立即以原路原速返回并交换角色,即由乙在地抽取任务单,与甲相遇时交给甲,由甲原地执行任务,乙继续向地前行.抽取和递交任务单的时间忽略不计.甲、乙两名同学之间的距离(米与运动时间(分之间的关系如图所示.已知甲的速度为每分钟60米,且甲的速度小于乙的速度,现给出以下结论:
①两地距离1680米;
②出发10分钟,甲乙两人第一次相遇;
③乙的速度为每分钟100米;
④甲在出发后第44分钟时开始执行任务.
其中正确的是 __.(写出所有正确结论的序号)
4、如图是某旅行车旅客携带行李收费示意图,小李所携带的行李重20千克,那么小李应该交费________(元).
5、在反比例函数中,已知四边形与四边形BOFE都是正方形,则点C的坐标为_________.
6、随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度(千米/时)与高架桥上每百米拥有车的数量(辆)的关系如图所示,当时,与成反比例函数关系,当车速度低于千米/时,交通就会拥堵,为避免出现交通拥堵,高架桥上每百米拥有车的数量应该满足的范围是________.
三、解答题(共 6 小题)
1、为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AC表示前3天的变化规律,第3天时硫化物的浓度降为4.5mg/L.从第3天起,所排污水中硫化物的浓度y与时间x满足下面表格中的关系:
时间x(天) 3 5 6 9 ……
硫化物的浓度y(mg/L) 4.5 2.7 2.25 1.5 ……
(1)在整改过程中,当0≤x<3时,硫化物的浓度y与时间x的函数表达式;
(2)在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;
(3)该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L?为什么?
2、如图,已知,在直角坐标系中,直线y= x+8与x轴、y轴分别交于点A、C,点P从A点开始以1个单位/秒的速度沿x轴向左移动,点Q从O点开始以2个单位/秒的速度沿y轴向上移动,如果P、Q两点同时出发.
(1)求点A、C的坐标;
(2)若点B在y轴上,且与点A、C构成以AC为腰的等腰三角形,请直接写出所有符合条件的B点坐标.
(3)经过几秒钟,能使△POQ的面积为8个平方单位.
3、一个城市的卫生状况反映了这个城市的文明程度.某城市每日清理垃圾的车辆有两种型号,已知2辆大型垃圾车与3辆小型垃圾车一次可以运输26吨垃圾;5辆大型垃圾车与4辆小型垃圾车一次可以运输58吨垃圾.
(1)求1辆大型垃圾车和1辆小型垃圾车一次各运输多少吨垃圾?
(2)已知该城市每日规定派出两种垃圾车共12辆,每辆大型垃圾车一次需费用300元,每辆小型垃圾车一次需费用150元.经调查该城市每日需运输的垃圾不少于60吨,请确定费用最少的派车方案,并求出最少费用是多少?
4、已知图中的曲线是反比例函数y=(m为常数)图象的一支.
(1)根据图象位置,求m的取值范围;
(2)若该函数的图象任取一点A,过A点作x轴的垂线,垂足为B,当△OAB的面积为4时,求m的值.
5、如下图,在平面直角坐标系xOy中,直线与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长
(2)求点C和点D的坐标
(3)y轴上是否存在一点P,使得?若存在,直接写出点P的坐标;若不存在,请说明理由
6、在近期“抗疫”期间,某药店销售、两种型号的口罩,已知销售800只型和450只型的利润为210元,销售400只型和600只型的利润为180元.
(1)求每只型口罩和型口罩的销售利润;
(2)该药店计划一次购进两种型号的口罩共2000只,其中型口罩的进货量不少于型口罩的进货量且不超过它的3倍,设购进型口罩只,这2000只口罩的销售总利润为元.
①求关于的函数关系式,并求出自变量的取值范围;
②该药店购进型、型口罩各多少只,才能使销售总利润最大?
班级:________ 姓名:________
一、单选题(共 8 小题)
1、某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)与该校参加竞赛人数的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图像上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( )
A.甲 B.乙 C.丙 D.丁
2、如图,已知直线与坐标轴分别交于、两点,那么过原点且将的面积平分的直线的解析式为( )
A. B. C. D.
3、小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )
A.2.7分钟 B.2.8分钟 C.3分钟 D.3.2分钟
4、弹簧的长度y(cm)与所挂物体的质量x(kg)的关系是一次函数,如图所示,此函数的图象经过A(﹣20,0),B(20,20)两点,则弹簧不挂物体时的长度是( )
A.9cm B.10cm C.10.5cm D.11cm
5、甲、乙两人在笔直的公路上同起点、同终点、同方向匀速步行1200米,先到终点的人原地休息.已知甲先出发3分钟,在整个步行过程中,甲、乙两人之间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①乙用6分钟追上甲;②乙步行的速度为60米/分;③乙到达终点时,甲离终点还有400米;④整个过程中,甲乙两人相距180米有2个时刻,分别是t=18和t=24.其中正确的结论有( )个
A.1 B.2 C.3 D.4
6、如图,在中,点是和两个内角平分线的交点,过点作分别交,于点,,已知的周长为8,,的周长为,则表示与的函数图象大致是( )
B.
C. D.
7、如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流与电阻成反比例函数的图象,该图象经过点.根据图象可知,下列说法正确的是( )
A.当时, B.I与R的函数关系式是
C.当时, D.当时,I的取值范围是
8、一杠杆装置如图,杆的一端吊起一桶水,水桶对杆的拉力的作用点到支点的杆长固定不变.甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力、、、,将相同重量的水桶吊起同样的高度,若,则这四位同学对杆的压力的作用点到支点的距离最远的是( )
A.甲同学 B.乙同学 C.丙同学 D.丁同学
二、填空题(共 6 小题)
1、已知点A在反比例函数的图象上,点B在x轴正半轴上,若为等腰三角形,且腰长为5,则的长为__________.
2、、两地在一条笔直的公路上,甲从地出发前往地、乙从地出发前往地,两人同时出发,甲到达地后停止,乙继续前进到达地,如图表示两人的距离(米与时间(分间的函数关系,则下列结论中:①、两地的距离是1200米;②两人出发4分钟相遇;③甲的速度是100米分;④乙出发12分钟到达地,正确的有 __(填序号)
3、甲、乙两名同学参加户外拓展活动,过程如下:甲、乙分别从直线赛道、两端同时出发,匀速相向而行.相遇时,甲将出发时在地抽取的任务单递给乙后继续向地前行,乙就原地执行任务,用时14分钟,再继续向地前行,此时甲尚未到达地.当甲和乙分别到达地和地后立即以原路原速返回并交换角色,即由乙在地抽取任务单,与甲相遇时交给甲,由甲原地执行任务,乙继续向地前行.抽取和递交任务单的时间忽略不计.甲、乙两名同学之间的距离(米与运动时间(分之间的关系如图所示.已知甲的速度为每分钟60米,且甲的速度小于乙的速度,现给出以下结论:
①两地距离1680米;
②出发10分钟,甲乙两人第一次相遇;
③乙的速度为每分钟100米;
④甲在出发后第44分钟时开始执行任务.
其中正确的是 __.(写出所有正确结论的序号)
4、如图是某旅行车旅客携带行李收费示意图,小李所携带的行李重20千克,那么小李应该交费________(元).
5、在反比例函数中,已知四边形与四边形BOFE都是正方形,则点C的坐标为_________.
6、随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度(千米/时)与高架桥上每百米拥有车的数量(辆)的关系如图所示,当时,与成反比例函数关系,当车速度低于千米/时,交通就会拥堵,为避免出现交通拥堵,高架桥上每百米拥有车的数量应该满足的范围是________.
三、解答题(共 6 小题)
1、为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AC表示前3天的变化规律,第3天时硫化物的浓度降为4.5mg/L.从第3天起,所排污水中硫化物的浓度y与时间x满足下面表格中的关系:
时间x(天) 3 5 6 9 ……
硫化物的浓度y(mg/L) 4.5 2.7 2.25 1.5 ……
(1)在整改过程中,当0≤x<3时,硫化物的浓度y与时间x的函数表达式;
(2)在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;
(3)该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L?为什么?
2、如图,已知,在直角坐标系中,直线y= x+8与x轴、y轴分别交于点A、C,点P从A点开始以1个单位/秒的速度沿x轴向左移动,点Q从O点开始以2个单位/秒的速度沿y轴向上移动,如果P、Q两点同时出发.
(1)求点A、C的坐标;
(2)若点B在y轴上,且与点A、C构成以AC为腰的等腰三角形,请直接写出所有符合条件的B点坐标.
(3)经过几秒钟,能使△POQ的面积为8个平方单位.
3、一个城市的卫生状况反映了这个城市的文明程度.某城市每日清理垃圾的车辆有两种型号,已知2辆大型垃圾车与3辆小型垃圾车一次可以运输26吨垃圾;5辆大型垃圾车与4辆小型垃圾车一次可以运输58吨垃圾.
(1)求1辆大型垃圾车和1辆小型垃圾车一次各运输多少吨垃圾?
(2)已知该城市每日规定派出两种垃圾车共12辆,每辆大型垃圾车一次需费用300元,每辆小型垃圾车一次需费用150元.经调查该城市每日需运输的垃圾不少于60吨,请确定费用最少的派车方案,并求出最少费用是多少?
4、已知图中的曲线是反比例函数y=(m为常数)图象的一支.
(1)根据图象位置,求m的取值范围;
(2)若该函数的图象任取一点A,过A点作x轴的垂线,垂足为B,当△OAB的面积为4时,求m的值.
5、如下图,在平面直角坐标系xOy中,直线与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长
(2)求点C和点D的坐标
(3)y轴上是否存在一点P,使得?若存在,直接写出点P的坐标;若不存在,请说明理由
6、在近期“抗疫”期间,某药店销售、两种型号的口罩,已知销售800只型和450只型的利润为210元,销售400只型和600只型的利润为180元.
(1)求每只型口罩和型口罩的销售利润;
(2)该药店计划一次购进两种型号的口罩共2000只,其中型口罩的进货量不少于型口罩的进货量且不超过它的3倍,设购进型口罩只,这2000只口罩的销售总利润为元.
①求关于的函数关系式,并求出自变量的取值范围;
②该药店购进型、型口罩各多少只,才能使销售总利润最大?
