17.2勾股定理的逆定理 课后测评(无答案)2022-2023学年人教版八年级数学下册
文档属性
| 名称 | 17.2勾股定理的逆定理 课后测评(无答案)2022-2023学年人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 225.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-18 14:14:56 | ||
图片预览


文档简介
人教版八年级数学下册17.2勾股定理的逆定理课后测评
一、单选题
1、如图,在中,点是上一点,连接,,,,,则的长为( )
A.5 B.4 C.3 D.2
2、已知a、b、c是三角形的三边长,若满足,则这个三角形的形状是( )
A.等腰三角形 B.等边三角形 C.锐角三角形 D.直角三角形
3、若将三条高线长度分别为x,y,z的三角形记为(x,y,z),则以下三角形(6,8,10),(8,15,17),(12,15,20),(20,21,29)中,直角三角形的个数为( ).
A.1个 B.2个 C.3个 D.4个
4、如图,在△ABC中,AB=8,BC=10,AC=6,则BC边上的高AD为( )
A.8 B.9 C. D.10
5、下列命题中,真命题是( )
A.如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B.如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C.若三角形三边长的比为1:2:3,则这个三角形是直角三角形
D.如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为
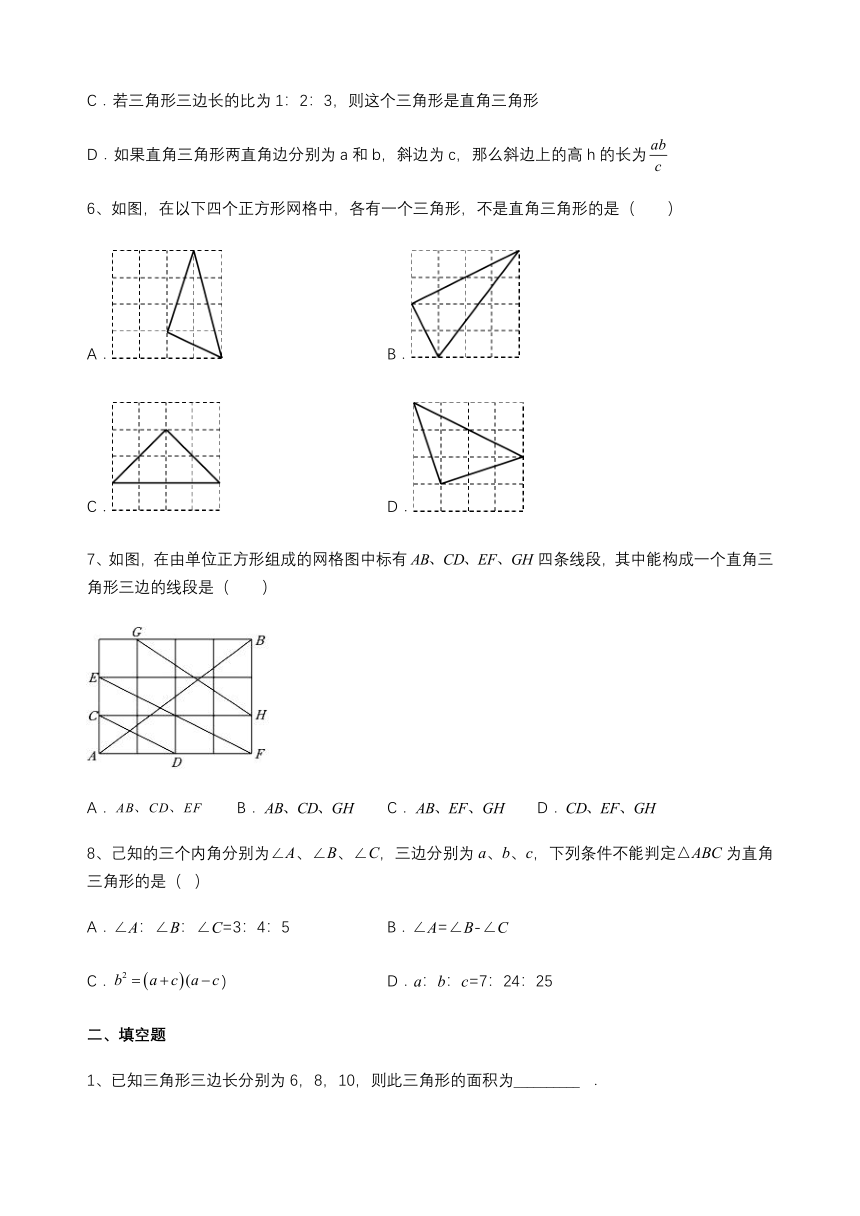
6、如图,在以下四个正方形网格中,各有一个三角形,不是直角三角形的是( )
A. B.
C. D.
7、如图,在由单位正方形组成的网格图中标有四条线段,其中能构成一个直角三角形三边的线段是( )
A. B. C. D.
8、己知的三个内角分别为∠A、∠B、∠C,三边分别为a、b、c,下列条件不能判定△ABC为直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.∠A=∠B-∠C
C.) D.a:b:c=7:24:25
二、填空题
1、已知三角形三边长分别为6,8,10,则此三角形的面积为__________ .
2、同一平面内有,,三点,,两点之间的距离为,点到直线的距离为,且为直角三角形,则满足上述条件的点有______个.
3、如图,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为__________.
4、如图,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36 cm,点P从点A开始沿AB边向B点以每秒1 cm的速度移动,点Q从点B沿BC边向点C以每秒2 cm的速度移动,如果同时出发,则过3 s时,△BPQ的面积为__________cm2.
5、如图,AB⊥CD于B,△ABD和△BCE都是等腰直角三角形,如果CD=17,BE=5,那么AC的长为_______
6、如图,点P是等边△ABC内的一点,PA=6,PB=8,PC=10,若点P′是△ABC外的一点,且△P′AB≌△PAC,则∠APB的度数为___.
三、解答题
1、有一块四边形草地(如图),测得m,m,m,.
(1)求的度数;
(2)求四边形草地的面积.
2、如图,网格中每个小正方形的边长都为1,点A,点B均为网格上的格点.
(1)______.
(2)若格点上存在点C,使,请在图中标出所有满足条件的格点C.
3、年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角清理出了一块可以绿化的空地.如图,已知,,,,技术人员在只有卷尺的情况下,通过测量某两点之间距离,便快速确定了.
(1)请写出技术人员测量的是哪两点之间的距离以及确定的依据;
(2)若平均每平方米空地的绿化费用为元,试计算绿化这片空地共需花费多少元?
4、我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)下列四边形是勾股四边形的有 .(填序号)
①长方形;②平行四边形;③正方形;
(2)如图1,已知格点(小正方形的顶点)O(0,0),A(0,4),B(3,0),请你直接写出所有以格点为顶点,OA、OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标____________
(3)如图2,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD、DC,已知∠DCB=30°.求证:四边形ABCD是勾股四边形.
5、已知△ABC中,AB=AC,BC=20,D是AB上一点,且CD=16,BD=12,
(1)求证:CD⊥AB;
(2)求三角形ABC的周长.
6、如图,在四边形中,,,.则,请说明理由.
一、单选题
1、如图,在中,点是上一点,连接,,,,,则的长为( )
A.5 B.4 C.3 D.2
2、已知a、b、c是三角形的三边长,若满足,则这个三角形的形状是( )
A.等腰三角形 B.等边三角形 C.锐角三角形 D.直角三角形
3、若将三条高线长度分别为x,y,z的三角形记为(x,y,z),则以下三角形(6,8,10),(8,15,17),(12,15,20),(20,21,29)中,直角三角形的个数为( ).
A.1个 B.2个 C.3个 D.4个
4、如图,在△ABC中,AB=8,BC=10,AC=6,则BC边上的高AD为( )
A.8 B.9 C. D.10
5、下列命题中,真命题是( )
A.如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B.如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C.若三角形三边长的比为1:2:3,则这个三角形是直角三角形
D.如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为
6、如图,在以下四个正方形网格中,各有一个三角形,不是直角三角形的是( )
A. B.
C. D.
7、如图,在由单位正方形组成的网格图中标有四条线段,其中能构成一个直角三角形三边的线段是( )
A. B. C. D.
8、己知的三个内角分别为∠A、∠B、∠C,三边分别为a、b、c,下列条件不能判定△ABC为直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.∠A=∠B-∠C
C.) D.a:b:c=7:24:25
二、填空题
1、已知三角形三边长分别为6,8,10,则此三角形的面积为__________ .
2、同一平面内有,,三点,,两点之间的距离为,点到直线的距离为,且为直角三角形,则满足上述条件的点有______个.
3、如图,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为__________.
4、如图,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36 cm,点P从点A开始沿AB边向B点以每秒1 cm的速度移动,点Q从点B沿BC边向点C以每秒2 cm的速度移动,如果同时出发,则过3 s时,△BPQ的面积为__________cm2.
5、如图,AB⊥CD于B,△ABD和△BCE都是等腰直角三角形,如果CD=17,BE=5,那么AC的长为_______
6、如图,点P是等边△ABC内的一点,PA=6,PB=8,PC=10,若点P′是△ABC外的一点,且△P′AB≌△PAC,则∠APB的度数为___.
三、解答题
1、有一块四边形草地(如图),测得m,m,m,.
(1)求的度数;
(2)求四边形草地的面积.
2、如图,网格中每个小正方形的边长都为1,点A,点B均为网格上的格点.
(1)______.
(2)若格点上存在点C,使,请在图中标出所有满足条件的格点C.
3、年是第六届全国文明城市创建周期的第三年,是“强基固本、全力冲刺”的关键之年.“创城”,既能深入改变一座城市的现代化进程,也能深刻影响生活在此间的人们.某小区在社区管理人员及社区居民的共同努力之下,在临街的拐角清理出了一块可以绿化的空地.如图,已知,,,,技术人员在只有卷尺的情况下,通过测量某两点之间距离,便快速确定了.
(1)请写出技术人员测量的是哪两点之间的距离以及确定的依据;
(2)若平均每平方米空地的绿化费用为元,试计算绿化这片空地共需花费多少元?
4、我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)下列四边形是勾股四边形的有 .(填序号)
①长方形;②平行四边形;③正方形;
(2)如图1,已知格点(小正方形的顶点)O(0,0),A(0,4),B(3,0),请你直接写出所有以格点为顶点,OA、OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标____________
(3)如图2,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD、DC,已知∠DCB=30°.求证:四边形ABCD是勾股四边形.
5、已知△ABC中,AB=AC,BC=20,D是AB上一点,且CD=16,BD=12,
(1)求证:CD⊥AB;
(2)求三角形ABC的周长.
6、如图,在四边形中,,,.则,请说明理由.
