8.4.1 平面 课件(共32张PPT)
文档属性
| 名称 | 8.4.1 平面 课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 50.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-16 16:51:10 | ||
图片预览









文档简介
(共32张PPT)
平面
纯粹几何学的学说往往会给出,而在许多问题中会给出多个简单而自然的办法来泂察诸真理的来源,去揭露那连接它们的神秘链索,去使它们独特地、明白地、完全地被认识。
——卓斯拿斯
8.4.1
学习目标
TARGET
平面概念
点、直线、平面、位置关系
基本事实
课堂小结
平面概念
纯粹几何学的学说往往会给出,而在许多问题中会给出多个简单而自然的办法来泂察诸真理的来源,去揭露那连接它们的神秘链索,去使它们独特地、明白地、完全地被认识。
——卓斯拿斯
平面概念
立体几何中许多元素的概念都是通过对现实几何体进行数学抽象后得到,例如直线,点。
生活中光滑的桌面,平静的湖面等都是我们熟知的平面,数学中平面的概念同样可以在这些现实平面的基础上加以抽象。
平面概念
平面的特征
平面的表示
没有大小、没有厚度,可无限延展
几何上通常用平行四边形来表示平面
平面概念
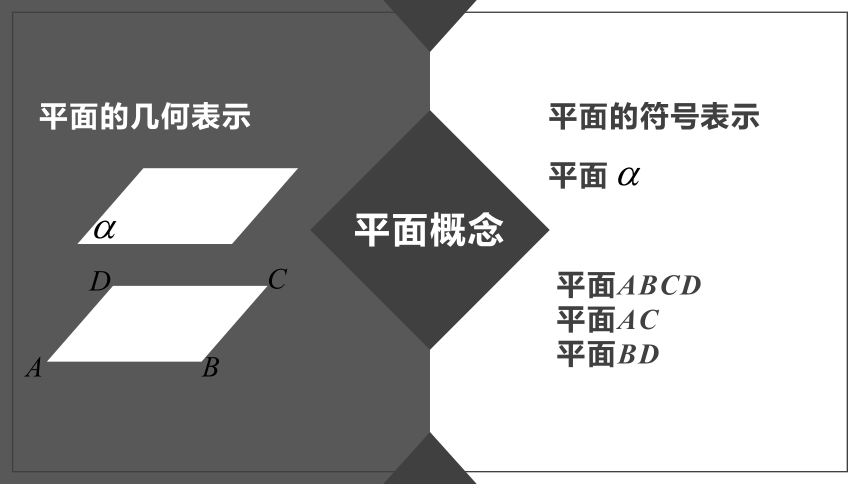
平面的几何表示
平面的符号表示
平面
平面ABCD
平面AC
平面BD
点、直线、平面的位置关系
纯粹几何学的学说往往会给出,而在许多问题中会给出多个简单而自然的办法来泂察诸真理的来源,去揭露那连接它们的神秘链索,去使它们独特地、明白地、完全地被认识。
——卓斯拿斯
点、直线、平面的位置关系
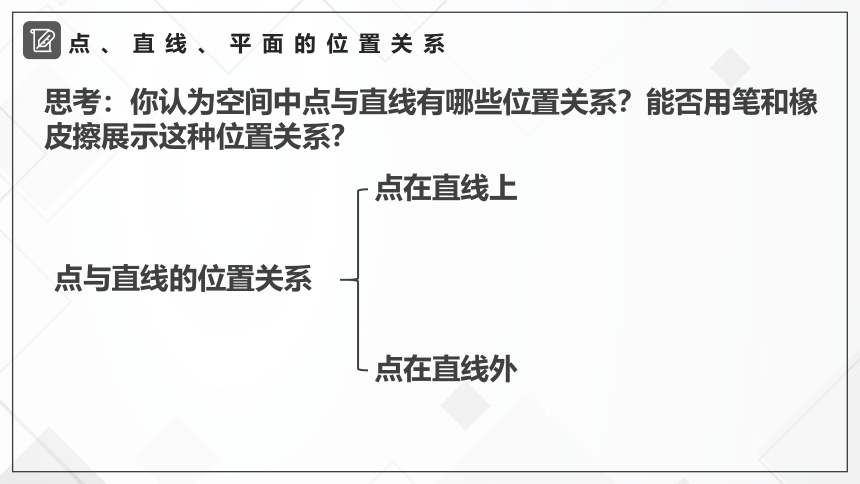
思考:你认为空间中点与直线有哪些位置关系?能否用笔和橡皮擦展示这种位置关系?
点与直线的位置关系
点在直线上
点在直线外
........ui98/8y7u663.............
点、直线、平面的位置关系
点与直线的位置关系
文字语言 符号语言 图形语言
点A在直线l上 A∈l
点A在直线l外 A l
A
l
l
A
........ui98/8y7u663.............
点、直线、平面的位置关系
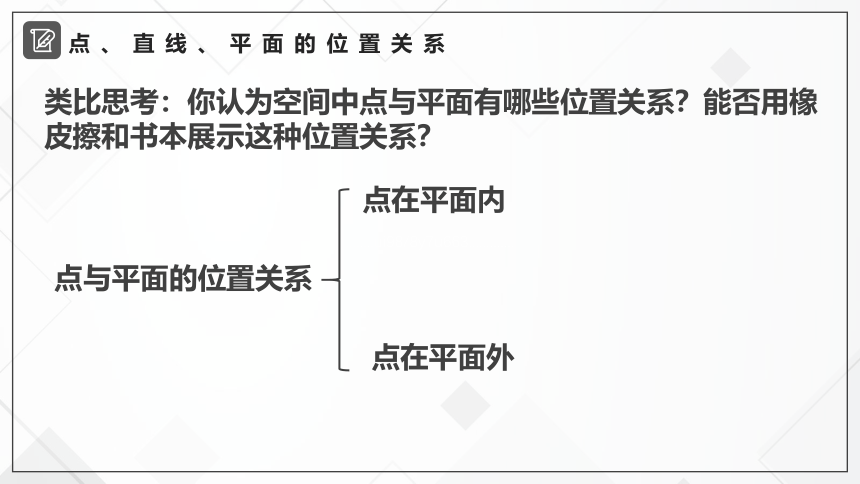
类比思考:你认为空间中点与平面有哪些位置关系?能否用橡皮擦和书本展示这种位置关系?
点与平面的位置关系
点在平面内
点在平面外
........ui98/8y7u663.............
点、直线、平面的位置关系
点与平面的位置关系
文字语言 符号语言 图形语言
点A在平面α内 A∈α
点A在平面α外 A α
α
α
A
A
........ui98/8y7u663.............
点、直线、平面的位置关系
类比思考:你认为空间中直线与平面有哪些位置关系?能否用笔和书本展示这种位置关系?
直线与平面的位置关系
直线在平面内
直线在平面外
........ui98/8y7u663.............
点、直线、平面的位置关系
直线与平面的位置关系
文字语言 符号语言 图形语言
直线 l 在平面α内
直线 l 在平面α外
α
α
l
l
........ui98/8y7u663.............
点、直线、平面的位置关系
课堂任务:借助两本书作为参考,画出两个相交的平面
思考:如何用符号语言描述两个平面相交于直线 l ?
基本事实
纯粹几何学的学说往往会给出,而在许多问题中会给出多个简单而自然的办法来泂察诸真理的来源,去揭露那连接它们的神秘链索,去使它们独特地、明白地、完全地被认识。
——卓斯拿斯
........ui98/8y7u663.............
思考:摄影器材的支架为什么都是三脚架?
基本事实
思考:试从三角架的原理中进行归纳总结需要哪些的元素才能确定唯一的平面?
怎样才能确定唯一的平面?怎样才能确定唯一的平面?
基本事实
基本事实1
过不在一条直线上的三个点,有且只有一个平面
A
B
C
怎样才能确定唯一的平面?怎样才能确定唯一的平面?
课堂活动
请同学们拿出一支笔和一个笔记本,如果将笔抽象成线,笔记本抽象成平面,将笔的一端固定在笔记本上。
思考:
能否判断直线在平面内?
要使直线在平面内,直线与平面至少需要有几个公共点?
基本事实
基本事实
基本事实2
如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内
A
B
α
A∈l,B∈l,且A∈α,B∈α
l
基本事实
活动:将笔记本立在桌面上
1
思考:笔记本所在的平面与桌面是否只交于一个点?
2
怎样才能确定唯一的平面?怎样才能确定唯一的平面?
基本事实
基本事实3
如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
P∈α,且P∈β
怎样才能确定唯一的平面?怎样才能确定唯一的平面?
基本事实
两个点
公共点
三个点
(点面)
(线面)
(面面)
怎样才能确定唯一的平面?怎样才能确定唯一的平面?
推论
推论1
经过一条直线和这条直线外一点,有且只有一个平面.
怎样才能确定唯一的平面?怎样才能确定唯一的平面?
推论
推论2
经过两条相交的直线,有且只有一个平面.
α
l
m
怎样才能确定唯一的平面?怎样才能确定唯一的平面?
推论
α
推论3
经过两条平行的直线,有且只有一个平面.
l
m
课堂练习
下列说法正确的是( )
A.平面的形状是平行四边形
B.一条直线和一个点可以确定一个平面
C.梯形可以确定一个平面
D.三点确定一个平面
C
课堂练习
判断下列说法的是否正确
(1)书桌面是平面( )
(2)平面α与平面β相交,它们只有有限个公共点( )
(3)如果两个平面有三个不共线的公共点,那么这两个平面重合( )
课堂练习
空间中相交于一点的三条直线,可以确定的平面个数是________________
一个或三个
课堂小结
纯粹几何学的学说往往会给出,而在许多问题中会给出多个简单而自然的办法来泂察诸真理的来源,去揭露那连接它们的神秘链索,去使它们独特地、明白地、完全地被认识。
——卓斯拿斯
课堂小结
知识收获
方法收获
其他收获
思想收获
分享你在本堂课中的收获
课后作业
教材131页 习题8.4——2,6
攀登几何的高峰
—END—
纯粹几何学的学说往往会给出,而在许多问题中会给出多个简单而自然的办法来泂察诸真理的来源,去揭露那连接它们的神秘链索,去使它们独特地、明白地、完全地被认识。
——卓斯拿斯
平面
纯粹几何学的学说往往会给出,而在许多问题中会给出多个简单而自然的办法来泂察诸真理的来源,去揭露那连接它们的神秘链索,去使它们独特地、明白地、完全地被认识。
——卓斯拿斯
8.4.1
学习目标
TARGET
平面概念
点、直线、平面、位置关系
基本事实
课堂小结
平面概念
纯粹几何学的学说往往会给出,而在许多问题中会给出多个简单而自然的办法来泂察诸真理的来源,去揭露那连接它们的神秘链索,去使它们独特地、明白地、完全地被认识。
——卓斯拿斯
平面概念
立体几何中许多元素的概念都是通过对现实几何体进行数学抽象后得到,例如直线,点。
生活中光滑的桌面,平静的湖面等都是我们熟知的平面,数学中平面的概念同样可以在这些现实平面的基础上加以抽象。
平面概念
平面的特征
平面的表示
没有大小、没有厚度,可无限延展
几何上通常用平行四边形来表示平面
平面概念
平面的几何表示
平面的符号表示
平面
平面ABCD
平面AC
平面BD
点、直线、平面的位置关系
纯粹几何学的学说往往会给出,而在许多问题中会给出多个简单而自然的办法来泂察诸真理的来源,去揭露那连接它们的神秘链索,去使它们独特地、明白地、完全地被认识。
——卓斯拿斯
点、直线、平面的位置关系
思考:你认为空间中点与直线有哪些位置关系?能否用笔和橡皮擦展示这种位置关系?
点与直线的位置关系
点在直线上
点在直线外
........ui98/8y7u663.............
点、直线、平面的位置关系
点与直线的位置关系
文字语言 符号语言 图形语言
点A在直线l上 A∈l
点A在直线l外 A l
A
l
l
A
........ui98/8y7u663.............
点、直线、平面的位置关系
类比思考:你认为空间中点与平面有哪些位置关系?能否用橡皮擦和书本展示这种位置关系?
点与平面的位置关系
点在平面内
点在平面外
........ui98/8y7u663.............
点、直线、平面的位置关系
点与平面的位置关系
文字语言 符号语言 图形语言
点A在平面α内 A∈α
点A在平面α外 A α
α
α
A
A
........ui98/8y7u663.............
点、直线、平面的位置关系
类比思考:你认为空间中直线与平面有哪些位置关系?能否用笔和书本展示这种位置关系?
直线与平面的位置关系
直线在平面内
直线在平面外
........ui98/8y7u663.............
点、直线、平面的位置关系
直线与平面的位置关系
文字语言 符号语言 图形语言
直线 l 在平面α内
直线 l 在平面α外
α
α
l
l
........ui98/8y7u663.............
点、直线、平面的位置关系
课堂任务:借助两本书作为参考,画出两个相交的平面
思考:如何用符号语言描述两个平面相交于直线 l ?
基本事实
纯粹几何学的学说往往会给出,而在许多问题中会给出多个简单而自然的办法来泂察诸真理的来源,去揭露那连接它们的神秘链索,去使它们独特地、明白地、完全地被认识。
——卓斯拿斯
........ui98/8y7u663.............
思考:摄影器材的支架为什么都是三脚架?
基本事实
思考:试从三角架的原理中进行归纳总结需要哪些的元素才能确定唯一的平面?
怎样才能确定唯一的平面?怎样才能确定唯一的平面?
基本事实
基本事实1
过不在一条直线上的三个点,有且只有一个平面
A
B
C
怎样才能确定唯一的平面?怎样才能确定唯一的平面?
课堂活动
请同学们拿出一支笔和一个笔记本,如果将笔抽象成线,笔记本抽象成平面,将笔的一端固定在笔记本上。
思考:
能否判断直线在平面内?
要使直线在平面内,直线与平面至少需要有几个公共点?
基本事实
基本事实
基本事实2
如果一条直线上的两个点在一个平面内,那么这条直线在这个平面内
A
B
α
A∈l,B∈l,且A∈α,B∈α
l
基本事实
活动:将笔记本立在桌面上
1
思考:笔记本所在的平面与桌面是否只交于一个点?
2
怎样才能确定唯一的平面?怎样才能确定唯一的平面?
基本事实
基本事实3
如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
P∈α,且P∈β
怎样才能确定唯一的平面?怎样才能确定唯一的平面?
基本事实
两个点
公共点
三个点
(点面)
(线面)
(面面)
怎样才能确定唯一的平面?怎样才能确定唯一的平面?
推论
推论1
经过一条直线和这条直线外一点,有且只有一个平面.
怎样才能确定唯一的平面?怎样才能确定唯一的平面?
推论
推论2
经过两条相交的直线,有且只有一个平面.
α
l
m
怎样才能确定唯一的平面?怎样才能确定唯一的平面?
推论
α
推论3
经过两条平行的直线,有且只有一个平面.
l
m
课堂练习
下列说法正确的是( )
A.平面的形状是平行四边形
B.一条直线和一个点可以确定一个平面
C.梯形可以确定一个平面
D.三点确定一个平面
C
课堂练习
判断下列说法的是否正确
(1)书桌面是平面( )
(2)平面α与平面β相交,它们只有有限个公共点( )
(3)如果两个平面有三个不共线的公共点,那么这两个平面重合( )
课堂练习
空间中相交于一点的三条直线,可以确定的平面个数是________________
一个或三个
课堂小结
纯粹几何学的学说往往会给出,而在许多问题中会给出多个简单而自然的办法来泂察诸真理的来源,去揭露那连接它们的神秘链索,去使它们独特地、明白地、完全地被认识。
——卓斯拿斯
课堂小结
知识收获
方法收获
其他收获
思想收获
分享你在本堂课中的收获
课后作业
教材131页 习题8.4——2,6
攀登几何的高峰
—END—
纯粹几何学的学说往往会给出,而在许多问题中会给出多个简单而自然的办法来泂察诸真理的来源,去揭露那连接它们的神秘链索,去使它们独特地、明白地、完全地被认识。
——卓斯拿斯
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
