2014年湘教版八年级数学下册导学案(全册)
文档属性
| 名称 | 2014年湘教版八年级数学下册导学案(全册) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-24 00:00:00 | ||
图片预览




文档简介
2014
年
湘
教
版
数
学
八
年
级
下
册
导
学
案
学习目标:
1.了解直角三角形的判定定理和性质定理
2.会用定理解决有关问题
知识链接
1.三角形内角和是________,
2.若∠A=36°,则它的余角∠B=_______
3.画出AB边上的中线
自主探究
阅读课本第2至3页内容,并自主探究下列几个问题:
1.在△ABC中,如果∠A+∠B=90°,则∠C=____。
于是△ABC是__________.
由上可得:有两个角_______的三角形是直角三角形
2.如图,Rt△ABC中,CD是斜边AB上的中线,
(l)量一量斜边AB的长度=__________
(2)量一量斜边上的中线CD的长度=________
(3)于是有CD=__AB
由此可得:直角三角形斜边上的中线等于斜边的________
合作交流
根据以上探究过程,请你与小组成员一起交流,解决下列问题:
1.在△ABC中,∠ACB=90°CD⊥ ( http: / / www.21cnjy.com )AB,那么与∠B互余的角有______,_______, 与∠B相等的角有___________。
2. 如图,Rt△ABC中,CD是斜边AB上的中线,AB=8cm,
则 AD=____cm, BD=_____cm, CD=________cm
3.如图,CD是△ABC的中线,∠ACB=90°,∠CDB=110°,则∠A=__________
实践应用
已知,如图,CD是△ABC的AB边上的中线,CD= 1/2 AB,求证:△ABC是直角三角形
自主检测
1.在△ABC中,若∠A=25°,∠B=65°,此三角形为________三角形
2.直角三角形中,两锐角的平分线相交所成的角的度数是_________。
3.若∠A:∠B:∠C=2:3:5,则△ABC是_________三角形
4.已知,△ABC中,AB=AC,AD平分 ( http: / / www.21cnjy.com )∠BAC,点E为AC的中点,请你写一个正确的结论.________________________________
5.如图,AC∥BD, ∠A和∠B的平分线的平分线相交于E,则∠AEB等于多少度?为什么?
小结:今天我们学了什么?你还有什么疑惑吗?
导学内容:1 进一步掌握直角三角形的性质----直角三角形中,30度的角所对的边等于斜边的一半;
2 能利用直角三角形的性质解决一些实际问题。
导学重点:直角三角形的性质 导学难点:直角三角形性质的应用
导 学 程 序
导入新课
1.直角三角形有哪些性质?
2 按要求画图:
(1)画∠MON,使∠MON=30°,
(2)在OM上任意取点P,过P作ON的垂线PK,垂足为K,量一量PO,PK的长度,PO,PK有什么关系?
(3) 在OM上再取点Q,R,分别过Q,R ( http: / / www.21cnjy.com )作ON的垂线QD,RE,垂足分别为D,E,量一量QD,OQ,它们有什么关系?量一量RE,OR,它们有什么关系?
由此你发现了什么规律?
直角三角形中,如果有一个锐角等于 ,那么它所对的 等于 .
合作交流,探究新知
1 探究直角三角形中,如果有一个锐角等于30°,那么它所对的直角边为什么等于斜边的一半。如图,Rt△ABC中,∠A=30°,BC为什么会等于 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 AB?(提示:取AB的中点D,连结CD)
证明:取AB的中点D,连结CD则AD=BD
因为 CD为Rt△ABC斜边的中线
所以
又因为 ∠A=30°所以∠B=
所以 △CDB为 三角形
所以 BC=
所以 BC=
得出结论:
2 上面定理的逆定理:上面 ( http: / / www.21cnjy.com )问题中,把条件“∠A=30°”与结论“BC=1/2AB”交换,结论还成立吗?(证明过程讨论完成)得出结论:
三、巩固练习
1 几何中的运用
(1)在△ABC中,△C=90°,∠B=15°,DE垂直平分AB,垂足为点E,交BC边于点D,BD=16cm,则AC的长为______
(2)如图在△ABC中,若∠BAC=120°,AB=AC,AD⊥AC于点A,BD=3,则BC=______.
(3)在A岛周围20海里水域有暗礁,一轮船由西向东航行到O处时,发现A岛在北偏东60°的方向,且与轮船相距30 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 海里,该轮船如果不改变航向,有触礁的危险吗?
四、小结今天我们学习哪些内容?
1.直角三角形的性质:
2.直角三角形的判定:
直角三角形的性质和判定3
一、知识要点
1、直角三角形的性质:
(1)在直角三角形中,两锐角 ;
(2)在直角三角形中,斜边上的中线等于__________的一半;
(3)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于 ___________;
(4)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于___________。
2、 直角三角形的判定:
(1)有一个角等于_________的三角形是直角三角形;
(2)有两个角_____________的三角形是直角三角形;
(3)如果三角形一边上的中线等于这条边的________,那么这个三角形是直角三角形。
二、知识运用典型例题
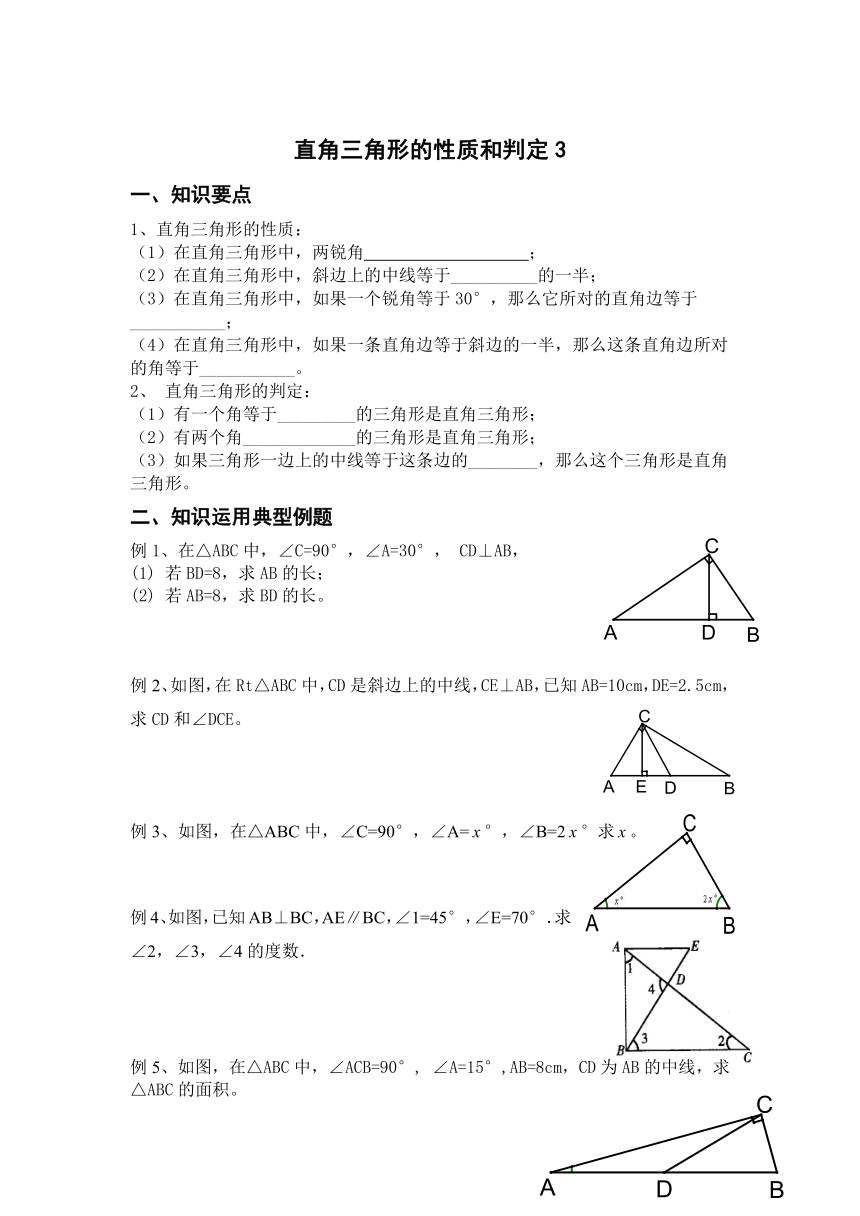
例1、在△ABC中,∠C=90°,∠A=30°, CD⊥AB,
(1) 若BD=8,求AB的长;
(2) 若AB=8,求BD的长。
例2、如图,在Rt△ABC中,CD是斜边上的中线,CE⊥AB,已知AB=10cm,DE=2.5cm,求CD和∠DCE。
例3、如图,在△ABC中,∠C=90°,∠A= HYPERLINK "http://www.21cnjy.com" °,∠B=2 HYPERLINK "http://www.21cnjy.com" °求 HYPERLINK "http://www.21cnjy.com" 。
例4、如图,已知AB⊥BC,AE∥BC,∠1=45°,∠E=70°.求∠2,∠3,∠4的度数.
例5、如图,在△ABC中,∠ACB=90°, ∠A=15°,AB=8cm,CD为AB的中线,求△ABC的面积。
例6、如图,在△ABC中,∠ACB=90°,AD=AC,BE=BC,求∠DCE的度数。
三、知识运用课堂训练
在Rt△ABC中,∠C=90°,AB=2cm,AC=BC,CD⊥AB于D点,则CD=_______cm;
如果三角形的两条边上的垂直平分线的交点在第三条边上,那么这个三角形是( )
A.锐角三角形 B.等腰三角形
C.直角三角形 D.钝角三角形
3、已知三角形的的三个内角的度数之比为1:2:3,它的最大边长为6cm,那么它的最小边长为_________cm;
4、直角三角形中一个锐角为30°,斜边和较小的边的和为12cm,则斜边长为_____________;
5、如图,在△ABC中,∠ACB=90°,D是AB的中点,CD=4cm,∠B=30°,
则AC=_____cm
6、将一张长方形纸片ABCD如图所示折叠,使顶点C落在C′点. 已知AB=2,∠DEC′=30°,则折痕DE的长为( )
A 、2 B、 HYPERLINK "http://www.21cnjy.com" C、4 D、1
知识运用课后训练
1、下列命题错误的是( )
A.有两个角互余的三角形一定是直角三角形;
B.在三角形中,若一边等于另一边的一半,则较小边的对角为30°;
C.直角三角形斜边上的中线等于斜边的一半;
D.△ABC中,若∠A:∠B:∠C=1:4:5,则这个三角形为直角三角形。
2、已知在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=4cm,则BC=_______cm,
∠BCD=_______,BD=_______cm,AD=________cm;
3、已知三角形的的三个内角的度数之比为1:2:3,且最短边是3厘米,则最长边上的中线等于____________;
在△ABC中,∠C=90°,∠A、∠B的平分线相交于O,则∠AOB=_________;
5、在△ABC中,∠BAC=90°,AC=5cm,AD是高,AE是斜边上的中线,且DC=1/2AC,求∠B 的度数及AE的长。
你在学习中还有什么没有弄懂的问题吗?
课题:直角三角形的性质和判定2第4课时
教学目标 1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。2.培养在实际生活中发现问题总结规律的意识和能力。
教学重点:勾股定理的内容及证明。
教学难点:勾股定理的内容及证明。
引直角△ABC的主要性质是:∠C=90°(用几何语言表示)(1)两锐角之间的关系: (2)若D为斜边中点,则斜边中线 (3)若∠B=30°,则∠B的对边和斜边: 二.探 自学内容:1、阅读教材P9至P11页;2、完成自主学习;3、并找出你存在的疑难,并用红笔标记。 (一)、1、(1)、同学们画一个直角边为3cm和4cm的直角△ABC,用 刻度尺量出AB的长。(2)、再画一个两直角边为5和12的直角△ABC,用刻度尺量AB的长 问题:你是否发现32+42与52,52+12和132的关系,即32+42 52,52+12 132,2、完成10页的探究,补充下表,你能发现正方形A、B、C的关系吗?A的面积(单位面积)B的面积(单位面积)C的面积(单位面积)图1图2由此我们可以得出什么结论?可猜想:命题1:如果直角三角形的两直角边分别为a、b,斜边为c,那么 。(二)、勾股定理的证明1、已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。求证:a2+b2=c2证明:4S△+S小正=S大正=根据的等量关系:由此我们得出:勾股定理的内容是: 。三.小结 四.用1、在Rt△ABC中, HYPERLINK "http://www.21cnjy.com" ,(1)如果a=3,b=4,则c=________;(2)如果a=6,b=8,则c=________;(3)如果a=5,b=12,则c=________;(4) 如果a=15,b=20,则c=________. 2、下列说法正确的是( )A.若 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 是△ABC的三边,则 a2+b2=c2B.若 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 是Rt△ABC的三边,则 a2+b2=c2C.若 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 是Rt△ABC的三边, HYPERLINK "http://www.21cnjy.com" , 则 a2+b2=c2D.若 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 是Rt△ABC的三边, HYPERLINK "http://www.21cnjy.com" ,则 a2+b2=c23、一个直角三角形中,两直角边长分别为3和4,下列说法正确的是( )A.斜边长为25 B.三角形周长为25 C.斜边长为5 D.三角形面积为204、如图,三个正方形中的两个的面积S1=25,S2=144,则另一个的面积S3为________.
课题:勾股定理综合应用
教学目标 1.会用勾股定理解决较综合的问题。2.树立数形结合的思想。
教学重点:勾股定理的综合应用。
教学难点:勾股定理的综合应用。。
引 复习勾股定理的内容。二.探 ( http: / / www.21cnjy.com )1.△ABC中,AB=AC=25cm,高AD=20cm,则BC= ,S△ABC= 。2.△ABC中,若∠A=1/2∠B=1 ( http: / / www.21cnjy.com )/2∠C,AC=10 cm,则∠A= 度,∠B= 度,∠C= 度,BC= ,S△ABC= 。例1:已知:在Rt△ABC中,∠C=90°,CD⊥BC于D,∠A=60°,CD= HYPERLINK "http://www.21cnjy.com" ,求线段AB的长。解答过程:例2:已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。解答过程:三.结 小结:不规则 ( http: / / www.21cnjy.com )图形的面积,可转化为特殊图形求解,本题通过将图形转化为直角三角形的方法,把四边形面积转化为三角形面积之差。四.用1. 如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,边长为无理数的边数是( )A. 0 B. 1 C. 2 D. 32. 如图所示,在△ABC中,三边a,b,c的大小关系是( )A.a<b<c B. c<a<b C. c<b<a D. b<a<c3.等边△ABC的高为3cm,以AB为边的正方形面积为 .4.如图,所有的四边形都是正方形, ( http: / / www.21cnjy.com )所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为_______cm25.若△ABC中,AB=13,AC=15,高AD=12,则BC的长是 .6.如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是 ;
课题:勾股定理逆定理
教学目标 1.体会勾股定理的逆定理得出过程,掌握勾股定理的逆定理。2.探究勾股定理的逆定理的证明方法。3.理解原命题、逆命题、逆定理的概念及关系。
教学重点:掌握勾股定理的逆定理及证明
教学难点:掌握勾股定理的逆定理
引问题一:1、怎样判 ( http: / / www.21cnjy.com )定一个三角形是直角三角形?2、下面的三组数分别是一个三角形的三边长a.b.c5、12、13 7、24、25 8、15、17(1)这三组数满足 a2+b2=c2吗?(2)分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?猜想命题2:如果三角形的三边长 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" ,满足 a2+b2=c2,那么这个三角形是 三角形问题二:命题1: 命题2: 命题1和命题2的 和 正好相反,把像这样的两个命题叫做 命题,如果把其中一个叫做 ,那么另一个叫做 二.探 自学内容:1、阅读教材P14至P15页;2、完成自主学习;3、并找出你存在的疑难,并用红笔标记。 例1 说出下列命题的逆命题,这些命题的逆命题成立吗?⑴同旁内角互补,两条直线平行。⑵如果两个实数的平方相等,那么两个实数平方相等。⑶线段垂直平分线上的点到线段两端点的距离相等。⑷直角三角形中30°角所对的直角边等于斜边的一半。例2 已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,a=n2-1,b=2n c= n2+1(n>1)求证:∠C=90°。三.结 师生小结勾股定理逆定理四.用1.判断题。⑴在一个三角形中,如果一边上的中线等于这条边的一半,那么这条边所对的角是直角。( ) ⑵命题:“在一个三角形中,有一个角是30°,那么它所对的边是另一边的一半。”的逆命题是真命题。( )⑶勾股定理的逆定理是:如果两条直角边的平方和等于斜边的平方,那么这个三角形是直角三角形。( )⑷△ABC的三边之比是1:1:√2 ,则△ABC是直角三角形。( )2.△ABC中∠A、∠B、∠C的对边分别是a、b、c,下列命题中的假命题是( )A.如果∠C-∠B=∠A,则△ABC是直角三角形。B.如果c2= b2 -a2,则△ABC是直角三角形,且∠C=90°。C.如果(c+a)(c-a)=b2,则△ABC是直角三角形。D.如果∠A:∠B:∠C=5:2:3,则△ABC是直角三角形。3.下列四条线段不能组成直角三角形的是( )A.a=8,b=15,c=17 B.a=9,b=12,c=15 C.a=√5 ,b=√3 ,c=√2 D.a:b:c=2:3:4
【教学目标】:
1、掌握直角三角形全等的判定定理,并能应用定理解决与直角三角形有关的问题。
2、进一步掌握推理证明的方法,拓发展演绎推理能力,培养思维能力。
【教学重难点】:
理解,掌握直角三角形全等的条件:HL.
【自学指导】:
一 、学生看P13---P14并思考一下问题:
“HL”中“H”代表什么?“L”代表什么?“HL”表示的是什么意思?
如何验证“HL”可以判定两个三角形全等?
到目前为止,我们学习了几种三角形全等的判别方法?各是什么?那么对于直角三角形全等的判别方法有几种?
运用“HL”证明直角三角形全等通常写成什么格式?
通常写成下面的格式:
在Rt△ABC与Rt△DEF中,
∵
∴Rt△ABC≌Rt△DEF(HL)
二、自学检测:
1.请判断满足下列条件的两个直角三角形是否全等,若不全等,在括号内打“×”,若全等,在括号内注明理由。
1.一个锐角和这个锐角的对边对应相等; ( )
2.一个锐角及和锐角相邻的一直角边对应相等;( )
3.一锐角与斜边对应相等; ( )
4.两直角边对应相等; ( )
5.两边分别相等; ( )
6.斜边和一条直角边对应相等的两个三角形. ( )
2.如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5) 若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
3.如图,AB⊥BD,CD∥AB,AB=CD,点E、F在BD上,且AE=CF.试说明AE∥CF.
三、师生共同探讨,总结:
@@@思考:证明线段相等,证明两个角相等我们现在用什么方法?由三角形全等到线段相等,角相等,还可由角相等到线平行。
四、例题讲解:
五、提高练习:
1.已知:如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=DC.证明:BE=DF
六、作业与学后反思:
1. 已知:如图,AB=CD, E、F在AC上,∠AFB=∠CED=90°,AE=CF.
(1)△ABF与△CDE全等吗?为什么?
(2)你发现AB与CD除相等外还有什么关系?如有就说明理由.
。
2. 如图,△ABC中,∠C=90°,AB=2AC,M是AB的中点,点N在BC上,MN⊥AB。
求证:AN平分∠BAC。
3. 如图,AB=CD,DF⊥AC于F,BE⊥AC于E,DF=BE,求证:AF=CE.
五.作业
课后反思
1.4角的平分线的性质(1)
学习目标:1、通过探究理解角平分线的性质并会运用2、掌握尺规作图作角平分线
学习重点:角平分线的性质及尺规作图
【学习过程】
一、预习导学:基本定理的学习:(阅读课文P22-25的内容)
角的平分线性质定理和判定定理:
二、讨论展示:
(1)知识回顾: 如图,已知AB=AD,BC=DC,求证:AC是∠DAB的平分线
(2)学习新知:
如图,已知∠BAC,用尺规作图的方法作出∠BAC的角平分线AD,
写出作法,并说明这种作法的依据。
2、OC是∠AOB的平分线,点P是射线OC上的任意一点,
操作测量:取点P的三个不同的位置,分 ( http: / / www.21cnjy.com )别过点P作PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:观察测量结果,猜想线段PD与PE的大小关系,写出结论
PD PE
第一次
第二次
第三次
3、你能用所学知识证明以上你发现的结论吗?
已知:AD平分∠BAC,P为AD上的一点,PM⊥AB,PN⊥AC
求证:
证明:
反过来,如图,若P为∠BAC内的一点,且点P到边AB、AC的距离相等,即PM=PN,你认为经过点P的射线AD平分∠BAC吗?为什么?
小结:通过以上探索和证明,我们得出了角平分线的性质是:
(1) ;
(2) 。
仔细比较分析,以上两条定理有什么关系:
一般情况下,我们要证明一个几何中的命题时,会按照类似的步骤进行,即:
(1) ;(2) ;(3) 。
三、新知应用:
(1)如图,已知AD是△ABC的角平分线,且D为BC的中点,DE⊥AB,DF⊥AC,
求证:BE=CF
2.1 多边形的内角和导学案
【学习目标】
1.知道多边形的内角和与外角和定理;
2.运用多边形内角和与外角和定理进行有关的计算.
【学习重难点】
重点:多边形的内角和与外角和定理; 难点:内角和定理的推导
【知识链接】
1.三角形的内角和是多少?
2.n边形从一个顶点出发的对角线有____条?它们将n边形分成____个三角形?
3.你知道长方形和正方形的内角和是多少?其它四边形的内角和是多少?
【合作探究】
知识点一:多边形的内角和定理
探究1:任意画一个四边形,量出它的4个内角,计算它们的和.再画几个四边形,量一量、算一算.
你能得出什么结论? 能否利用三角形内角和等于180°得出这个结论?
结论: .
探究2:从上面的问题,你能想出五边形和六边形的内角和各是多少吗?
观察图3,请填空:
(1)从五边形的一个顶点出发,可以引_____条对角线,它们将五边形分为_____个三角形,五边形的内角和等于180°×______.
(2)从六边形的一个顶点出发,可以引_____条对角线,它们将六边形分为_____个三角形,六边形的内角和等于180°×______.
探究3:一般地,怎样求n边形的内角和呢?请填空:
从n边形的一个顶点出发,可以引____条对角线,它们将n边形分为____个三角形,n边形的内角和等于180°×______.
结论:多边形的内角和与边数的关系是 .
练习:
1.十二边形的内角和是_________.
一个多边形的内角和等于900°,求它的边数.
知识点二:多边形的外角和
探究4:如图8,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
问题:如果将六边形换为n边形(n是大于等于3的整数),结果还相同吗?
因此可得结论: .
对应练习:
七边形的外角和是_________;十二边形的外角和是____________;三角形的外角和是_______.
一个多边形的每一个外角都等于36°则这个多边形是_______边形.
在每个内角都相等的多边形中,若一个外角是它相邻内角的1/2,则这个多边形是______边形.
【整理学案】通过本节课学习,你有什么收获?
【达标测试】
一个多边形的每一个外角都等于40° ( http: / / www.21cnjy.com ),则它的边数是__________;一个多边形的每一个内角都等于140°,则它的边数是___________.
如果四边形有一个角是直角,另外三个角的度数之比为2:3:4,那么这三个内角的度数分别为________.
3、若一个多边形的内角和为1080°,则它的边数是___________.
当一个多边形的边数增加1时,它的内角和增加_________度.
5、正十边形的一个外角为______.
6、_______边形的内角和与外角和相等.
7、已知一个多边形的内角和与外角和的差为1080°,则这个多边形是_____边形.
8、若一个多边形的内角和与外角和的比为7:2,求这个多边形的边数。
探 究:
把一块四边形的木料锯掉一个角后,所得的多边形的内角和为多少度?
多边形的内角和与外角和 习题精选(一)
1.n边形的内角和=________度,外角和=_______度。
2.从n边形(n>3)的一个顶点出发,可以画_______条对角线, ( http: / / www.21cnjy.com )这些对角线把n边形分成______三角形,分得三角形内角的总和与多边形的内角和_______。 ( http: / / www.21cnjy.com )
3.如果一个多边形的内角和与它的外角和相等,那么这个多边形是____边形。
4.如果一个多边形的内角和等于它的外角和5倍,那么这个多边形是____边形。
5.若n边形的每个内角都是150°,则n=____。
6.一个多边形的每个外角都是36°,这个多边形是______边形。
7.如果一个多边形的每个内角都相等,且内 ( http: / / www.21cnjy.com )角的度数是与它相邻的外角度数的2倍,那么这个边形的每个内角是_____度,其内角和等于______度。
8.若一个多边形的内角和是1800°,则这个多边形的边数是_______。
9.若一个多边形的边数增加1,则它的内角和 ( ) ( http: / / www.21cnjy.com )
A.不变 B.增加1 C.增加180° D.增加360°
10.当一个多边形的边数增加时,其外角和 ( )
A.增加 B.减少 C.不变 D.不能确定
11.某学生在计算四个多边形的内角和时,得到下列四个答案,其中错误的是( )
A.180° B.540° C.1900° D.1080°
12.分别画出下列各多边形的对角线,并观察图形完成下列问题:
(1)试写出用n边形的边数n表示对角线总条数S的式子:__________。
(2)从十五边形的一个顶点可以引出______条对角线,十五边形共有______条对角线:
(3)如果一个多边形对角线的条数与它的边数相等,求这个多边形的边数。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
13.n边形的内角和等于______度。任意多边形的外角和等于______度。
14.一个多边形的外角和是它的内角和的 ( http: / / www.21cnjy.com ),这个多边形是______边形。
15.如果十边形的每个内角都相等,那么它的每个内角都等于______度,每个外角都等于______度。
16.若多边形的内角和是1080°,则这个多边形是______边形。
17.如果一个多边形的内角和是720°,那么这个多边形的对角线的条数是( )
A.6 B.9 C.14 D.20
18.如果一个多边形的内角和是它的外角和的n倍,则这个多边形的边数是( )
A.n B.2n-2 C.2n D.2n+2
19.一个多边形截去一个角(不过顶点)后,形成的多边形的内角和是2520°,那么原多边形的边数是( )
A.13 B.14 C.15 D.13或15
20.若两个多边形的边数之比为1:2,两个多边形的内角和之和为1440°,求这两个多边形的边数。
21.判断:外角和等于内角和的多边形一定是四边形。( )
22.一个多边形的内角和是它的外角和的4倍,这个多边形是 ( )
A.四边形 B.六边形 C.八边形 D.十边形
23.一个多边形中,除一个内角外,其余各内角和是120°,则这个角的度数是( )
A.60° B.80° C.100° D.120°
24.如果一个多边形的内角和等于1800°,则这个多边形是______边形;如果一个n边形每一个内角都是135°,则=n______;
如果一个n边形每一个外角都是36°,则=n______。
25.某学校艺术馆的地板由三种正多边形的小木板铺成,设这三种多边形的边数分别为x、y、z,求 ( http: / / www.21cnjy.com )的值。
2.2.1平行四边形的性质学案1
一.温故知新:
1.有两组对边__________________的四边形叫平形四边形,平行四边形用“______”表示,平行四边形ABCD记作__________。
2.如图□ABCD中,对边有______组,分别是___________________,对角有_____组,分别是_________________,对角线有______条,它们是___________________。
二.学习新知:
1.自学课本P83~P84,填空:平行四边形的性质
(1)边:_________________________________________________________
(2)角:_________________________________________________________
例:□ABCD中,如果AB∥CD,那么AB=______,BC=______,∠A=______,∠B=______.
2.看例1,完成课本P84的练习.
三.释疑提高:
1.□ABCD中,两邻角之比为1∶2,则它的四个内角的度数分别是____________.
2.□ABCD的周长是28cm,△ABC的周长是22cm,则AC的长是__________.
3.如图,在□ABCD中,M、N是对角线BD上的两点,BN=DM,请判断AM与CN有怎样的数量关系,并说明理由.它们的位置关系如何呢?
( http: / / www.21cnjy.com )
4.如图,在□ABCD中,AE ( http: / / www.21cnjy.com )⊥BC于E,AF⊥CD于F,若∠EAF=60°,BE=2cm,DF=3cm,求□ABCD的周长和面积. 若问题改为CF=2cm,CE=3cm,求□ABCD的周长和面积.
( http: / / www.21cnjy.com )
5.□ABCD中,E在边AD上,以BE ( http: / / www.21cnjy.com )为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△FDE的周长为8,△FCB的周长为22,求CF的长.
( http: / / www.21cnjy.com )
四.小结归纳:
五.巩固检测
1.课本P—1、2 2.课堂作业平行四边形性质1
2.2.1平行四边形的性质学案2
一.温故知新:
1.平行四边形的定义是:_______________________________________________.
2.所学平行四边形的性质有:平行四边形的对边______________,平行四边形的对角______________.
3.如图,在□ABCD中,BC=2AB,M是AD的中点,则∠BMC=___________.
二.学习新知:
1.自学课本P85~86内容,填空:
平行四边形的又一个性质是:______________________________,当图形中没有平行四边形的对角线时,往往需作出对角线.
由此得到平行四边形的性质有:
(1)边:_____________ (2)角:_____________ (3)对角线:_____________
2.看例2,完成课本P86的练习.
三.释疑提高:
1.在□ABCD中,AC、B ( http: / / www.21cnjy.com )D交于点O,已知AB=8cm,BC=6cm,△AOB的周长是18cm,那么△AOD的周长是_____________.
2. □ABCD的对角线交于点O,S△AOB=2cm2,则S□ABCD=__________.
3. □ABCD的周长为60cm,对角 ( http: / / www.21cnjy.com )线交于点O,△BOC的周长比△AOB的周长小8cm,则AB=______cm,BC=_______cm.
4. □ABCD中,对角线AC和BD交于点O,若AC=8,AB=6,BD=m,那么m的取值范围是____________.
5. □ABCD中,E、F在AC上,四边形DEBF是平行四边形.求证:AE=CF.
( http: / / www.21cnjy.com )
6.如图,田村有一口四边形的池塘,在它 ( http: / / www.21cnjy.com )的四角A、B、C、D处均有一棵大桃树.田村准备开挖养鱼,想使池塘的面积扩大一倍,并要求扩建后的池塘成平行四边形形状,请问田村能否实现这一设想?若能,画出图形,说明理由.
( http: / / www.21cnjy.com )
四.小结归纳:
五.巩固检测
1.作业精编 2.课堂作业平行四边形性质2
2.2.2平行四边形的判定学案1
一.温故知新
1.如图在平行四边形ABCD中,DB=DC,∠A=65°,CE⊥BD于E,则∠BCE= .
2.如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F,已知AE=4,AF=6,□ABCD的周长为40,试求□ABCD的面积。
二.学习新知
1.自学课本P86-P87,掌握平行四边形的判定定理,注意定理条件和结论,并会证明。
2.自学例子,并证明。 独立完成P87的练习。
三.释疑提高
1.以不共线的三点A、B、C为顶点的平行四边形共有 个。
2.一个四边形的边长依次为a、b、c、d,且a2+b2+c2+d2=2ac+2bd,
这个四边形是 。
3.如图,在△ABC的边AB上截取AE=BF,过E作ED∥BC交AC于D,
过F作FG∥BC交AC于G,求证:ED+FG=BC。
( http: / / www.21cnjy.com )
4.如图,线段AB、CD相交于点O,AC∥DB,AO=BO,E、F分别为OC、OD的中点,连结AF、BE,求证AF∥BE。
5.如图,已知O是平行四边形ABCD对角 ( http: / / www.21cnjy.com )线AC的中点,过点O作直线EF分别交AB、CD于E、F两点,(1)求证:四边形AECF是平行四边形;(2)填空,不填辅助线的原因中,全等三角形共有 对。
6.如图,在□ABCD中,点E是AD的中点, ( http: / / www.21cnjy.com )BE的延长线与CD的延长线相交于点F,(1)求证:△ABE≌△DFE;(2)试连结BD、AF,判断四边形ABDF的形状,并证明你的结论。
四.小结归纳
五.巩固检测1.习题-1、4、5、8、9、10、11
2.2.2平行四边形的判定学案2
一.温故知新
1.如图在□ABCD中,EF∥AD,MN∥AB,EF、MN相交于点P,图中共有 个
平行四边形。
2.如果平行四边形的两条对角线长分别为8和12,那么它的边长不能取( )
A. 10 B. 8 C. 7 D. 6
3.如图,在□ABCD中,AC、BD ( http: / / www.21cnjy.com )交于点O,EF过点O分别交AB、CD于E、F,AO、CO的中点分别为G、H,求证:四边形GEHF是平行四边形。
二.学习新知
1.自学课本P88平行四边形的判定定理,注意定理条件和结论,并会证明。
2.自学例子,掌握三角形中位线概念和中位线定理,并会证明。
3.掌握平行线间的距离。 4.完成P90面练习1.2.3。
三.释疑提高
1.如图,△ABC是等边三角形,P是其 ( http: / / www.21cnjy.com )内任意一点,PD∥AB,PE∥BC,DE∥AC,若△ABC周长为8,则PD+PE+PF= 。
2.四边形ABCD是平行四边形,BE平分∠ABC交AD于E, DF平分∠ADC交BC于点F,求证:四边形BFDE是平行四边形。
3.已知□ABCD中,E、F分别是AD、BC的中点,AF与EB交于G,CE与DF交于H,求证:四边形EGFH为平行四边形。
4.如图,在四边形ABCD中,AB=6,BC=8,∠A=120°,∠B=60°,∠BCD=150°,求AD的长。
( http: / / www.21cnjy.com )
5.已知BE、CF分别为△ABC中∠B、∠C的平分线,AM⊥BE于M,AN⊥CF于N,求证MN∥BC。
( http: / / www.21cnjy.com )
6.如图,在□ABCD中,EF∥AB交BC于E,交AD于F,连结AE、BF交于点M,连结CF、DE交于点N,求证:(1)MN∥AD;(2)MN= HYPERLINK "http://www.21cnjy.com" AD。
四.小结归纳
八年级几何四边形练习题
1、已知四边形ABCD为正方形,M为AB中点,N为AD上一点,且CN=AB+AN.
求证:CM平分∠BCN.
已知如图, 四边形ABCD是平行四边形,E为AC上一点,F为AB上一点,
且AE=2EC,BF=2AF,若S
△BEF=2,求S□ABCD.
3、已知,四边形ABCD是平行四边形,EF垂直平分BD,垂足为O,
交BA、DC的延长线于E、F.求证:四边形EBFD为菱形.
4、如图,D为AB中点,DE∥BC交AC于E点.
5、如图梯形ABCD中,AD∥BC,E为AB中点,F为DC中点,EF、BD交于G点.
求证:G为BD中点.
6、如图△ABC中,∠B=90°,∠BAC=78°,FC∥AB,BC交AF于G点,
且FG=2AC.求∠BAG.
7、已知如图, 梯形ABCD中,E为DC中点,若梯形ABCD=10.
(1)求S△EBA.(2)若AB=AD+BC,求证:AE⊥BE.
8、已知如图, 四边形ABCD是矩形,AE平分∠BAD,EF交BD于F点,
交AC于G点,若GA=GE,求证:EF⊥BD.
9、已知如图D为△ABC边AB的中点,E在BC上,且BE= HYPERLINK "http://www.21cnjy.com" BC, 且CD、AE交于P点, 若S△APC=8,求S△ABC.
10、已知,如图,正方形ABCD中,AC、BD交于O点,EA平分∠BAC交BD于F点.求证:FO= HYPERLINK "http://www.21cnjy.com" EC.
11、已知如图, 四边形ABCD是平行四边形,
直线 HYPERLINK "http://www.21cnjy.com" 上有点M、N、P、Q,且BM⊥ HYPERLINK "http://www.21cnjy.com" ,
AN⊥ HYPERLINK "http://www.21cnjy.com" ,CP⊥ HYPERLINK "http://www.21cnjy.com" ,DQ⊥ HYPERLINK "http://www.21cnjy.com" .求证:DM+BQ=AN+CP.
正方形ABCD中,E为BC上一点,F为DC上一点,AE⊥BF,
连AC,O为AC中点,连OE、OF,求证:(1)BE=CF;(2)OE⊥OF;
(3)若S正方形=1,求S四边形OECF.
13、如图,等腰梯形ABCD中,AD∥BC,AB=CD.
(1)将△ABC沿BC向下翻折到△CBE的位置,试判断四边形DBEC的形状,并证明你的结论.
(2)翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点G、F,
若∠CBD=45°,AD=4,BC=8求BF的长。
14,如图,直线y= HYPERLINK "http://www.21cnjy.com" x+5与x轴、y轴交于A、B两点,过点C(-7,2)作CD⊥x轴于D,连CA.(1)求证:AC=AB,且AC⊥AB;(2)在y轴上取点E(0,3),连DE
交AB于点P,求∠APD的度数.
16、已知等腰梯形ABCD中,AD∥BC,AB=DC,点P是BC边上一点,PE⊥AB,PF⊥CD,BG⊥CD.求证:PE+PF=BG.
平行四边形测试题
一、选择题(每题3分,共30分)
1.在□ABCD中,∠A∶∠B∶∠C∶∠D的值可以是( )
A.1∶2∶3∶4 B.1∶2∶2∶1
C.1∶1∶2∶2 D.2∶1∶2∶1
2.平行四边行的两条对角线把它分成全等三角形的对数是( )
A.2 B.4 C.6 D.8
3.在□ABCD中,∠A、∠B的度数之比为5∶4,则∠C等于( )
A.60° B.80° C.100° D.120°
4、一个四边形的三个内角度数依次如下,那么其中是平行四边形的是( )
A、88°,108°,88° B、88°,104°,108°
C、88°、92°、92° D、88°,92°,88°
5、下列哪组条件能判别四边形ABCD是平行四边形?( )
A、AB∥CD,AD=BC B、AB=CD,AD=BC
C、∠A=∠B,∠C=∠D D、AB=AD,CB=CD
6、平行四边形的一边长为10,那么它的两条对角线的长度可以是( )
A、8和12 B、4和16 C、20和30 D、8和6
7. HYPERLINK "http://www.21cnjy.com" ABCD的周长为40 cm,△ABC的周长为25 cm,则对角线AC长为( )
A.5 cm B.15 cm C.6 cm D.16 cm
8.□ABCD的周长为36 cm,AB=5/7BC,则较长边的长为( )
A.15 cm B.7.5 cm C.21 cm D.10.5 cm
9.如图,□ABCD中,EF过对角线的交点O,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )A.8.3 B.9.6 C.12.6 D.13.6 HYPERLINK "http://www.21cnjy.com" (图9) (图10)
10.如图,在平面直角坐标系中, ( http: / / www.21cnjy.com )□ABCD的顶点A、B、D的坐标分别是(0,0),(5,0)(2,3),则顶点C的坐标是( )A.(3,7) B.(5,3) C.(7,3) D.(8,2)
二、填空题(本大题8个小题,每小题3分,共24分)
11、在平行四边形中,若一个角为其邻角的2倍,则这个平行四边形中两邻角的度数分别是 。
12、设点O是□ABCD对角线的交点,如果□ABCD的面积为20cm2,则△AOB的面积为 。
13、若平行四边形的一边长为8cm,一条对角线长为6cm,则另一条对角线长χ(cm)的取值范围为 。
14、□ABCD的周长为36cm,AB=8cm,则BC= cm。
15、已知平行四边形的面积为144,相邻两边上的高分别为8和9,则它的周长为 。
16、已知a、b、c、d为四边形的 ( http: / / www.21cnjy.com )四边长,a、c为对边,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形一定是 。
17.能判定四边形ABCD为平行四边形的题设是: 。(只填字母序号)
(A)AB∥CD,AD=BC; (B)∠A=∠B,∠C=∠D; (C)AB=CD,AD=BC;
(D)AB=AD,CB=CD (E)AB HYPERLINK "http://www.21cnjy.com" CD (F)AB∥CD,AD∥BC (G)OA=OC,OB=OD
18、如图,P为□ABCD的对角线B ( http: / / www.21cnjy.com )D上一点,过P作GH∥CD,EF∥BC,写出图中你认为面积相等的平行四边形有 。
(说明:可写成S □ABCD =S□ … … 的形式)
三、解答题(共46分)解答时请写出必要的演算过程或推理步骤。
19、(10分)已知:在□ABCD中,∠A的 20.(11分)如图,在□ABCD中,
角平分线交CD于E,若 HYPERLINK "http://www.21cnjy.com" , AB=8cm,BC=10cm,∠C=120°,
AB的长为8,求BC的长。 (1)求BC边上的高AH的长;
(2)求□ABCD的面积.
21、(12分)如图,AC是□ABCD的 22.(13分)如图,在△ABC中,AB=AC,
对角线,MN∥AC,分别交AD、CD 点D在BC上,DE∥AC,DF∥AB,
于点P、Q,试说明MP=QN。 (1)求证:FD=FC
(2)若AC=6cm,试求四边形AEDF的 周长。
中心对称和中心对称图形导学案P51
教学目标:
1、知道中心对称和中心对称图形的意义。
2、知道中心对称的两个图形的特征。
3、能运用中心对称的性质做出一个图形关于某点对称的中心对称图形。
教学重难点:
重点:1、中心对称图形和中心对称的概念及特征。
2、作已知图形关于某点为对称中心的中心对称图形。
难点:中心对称图形与中心对称之间的区别与联系。
任务一:探索中心对称的定义:
问题1:这些图形有什么共同的特征?
问题2:你能将上图中的图形绕某点旋转180°,使旋转后的图形与原图形完全重合吗?请选取其中的一个图形加以解释。
归纳总结:
在平面内,一个图形绕某个点旋转 ( http: / / www.21cnjy.com ) ,如果旋转前后的图形互相 ,那么这个图形叫做 ,这个点叫做它的 。
左图是一幅中心对称图形,O是 ( http: / / www.21cnjy.com )对称中心,请你找出点A绕点O的旋转180O后的对应点B;AO=BO吗?其他的对应点到对称中心的距离呢?由此你会得到怎样的结论?
任务二:学以致用:
1.下面哪个图形是中心对称图形?
2、下列图形是中心对称图形的是( )
3、在一次游戏当中,小明将下面左图的四张扑克牌中的一张旋转180O后,得到右图,小亮看完很快知道小明旋转了哪一张扑克,你知道为什么吗?
4、在26个英文大写正体字母中,哪些字母是中心对称图形
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
任务三:能力提升:
1、请以给定的图形○○△△ ( http: / / www.21cnjy.com )=(两个圆,两个三角形,两条平行线)为构件,尽可能多地构思有意义的一些中心图形,并写上一两句贴切,诙谐的解说词.如下图就是符合要求的图形,你能构思其它图形吗 比一比,看谁想得多,看谁想得妙!
2、举出常见的中心对称图形。
二、填空题(每题 3 分,共 12 分)
3.写出几个是中心对称的汉字:
4 .如图 15-3-3 所示, △OA B 绕点O旋转 180°得到 △OCD ,
连结 AD 、 BC ,得到四边形ABCD ,则 AB________CD (填位置
关系);与 △AOD成中心对称的是__________由此可得到 AD______ BC(填位置关系).
5 .从数学对称的角度看,下面几组大写英文字母: ① ANEG ; ② GBXM ; ③ XIHO ; ④ ZDWH .不同于另外三组的 ( http: / / www.1230.org / )-组是_________,这-组英文字母的特点是__________.
6.正方形既是_________图形,又是 ( http: / / www.21cnjy.com )_____________图形,它有_____________条对称轴,对称中心是_____________________
三、计算题( 10 分)
7 .如图所示,是跷跷板图,AO和BO等长, ( http: / / www.21cnjy.com )横板AB通过点O,且可以绕O点上下转动,如果∠OCA=90°,∠CAO= 25° ,问小孩玩跷跷板时上下最多可以转动多少度?
图
四、解答题(每题 10 分,共 20 分)
8.如图 15-3-5 所示,已知 MN⊥PQ , 垂足为O ,点 A 、A1 是以 MN 为轴的对称点,而点 A 、 A2 是以PQ 为轴的对称点,则点 A1、A2 关于点O成中心对称,你能说明其中的道理吗?
课题: 三角形的中位线
一 学习目标
1了解三角形的中位线的定义,注意与三角形的中线的区别
2 掌握三角形的中位线定理,并能灵活的运用
重点:识记三角形的中位线定义、定理
难点:三角形中位线定理的灵活应用
二 自主预习
1 三角形的中位线
连接三角形的两边 的线段,叫做三角形的中位线。
2 三角形的中位线定理
三角形的中位线平行于 ,并且等于 。
三 课内探究
探究一 三角形的中位线及其性质
任意画△ABC,设AB,AC边的中点分别为D,E,连接DE.
连接三角形 ,叫做 ,
画一画,三角形有几条中位线。
。
在图1中分别度量∠ADE与∠B的大小,你发现DE与BC有怎样的位置关系?
分别量出线段DE与BC的长,你发现DE与BC之间有怎样的数量关系?
?
对于△ABC其他的两条中位线,重复(2)中实验,你得到了什么结论?
归纳(2)(3)的结论,你认为三角形的中位线具有什么性质?
结论:
(5)如图,把△ABC沿中位线DE剪开,得到△ADE和四边形BCDE,将△ADE绕点E旋转1800,使点A与点C重合,你拼出一个什么图形?
上面(5)中得拼图过程对于证明你所发现的命题有什么启示?
(7)已知:如图,在△ABC中,点D,E分别是AB与AC边的中点。
求证:DE∥BC,DE= HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 BC
于是就证明了(2)中发现的命题,我们把它叫做三角形的中位线定理
三角形的中位线定理:
三角形中位线的应用
1 .如图所示,□ ABCD的对角线AC,BD相交于点O,AE=EB,求证:OE∥BC.
2.如图所示,在△ABC中,点D在BC上且CD=CA,CF平分∠ACB,AE=EB,求证:EF= HYPERLINK "http://www.21cnjy.com" BD.
3.如图所示,已知在□ABCD中,E,F分别是AD,BC的中点,求证:MN∥BC.
4.已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
5.已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.
求证:四边形DEFG是平行四边形.
6.已知:如图,E为□ABCD中DC边的延长线上的一点,且CE=DC,连结AE
分别交BC、BD于点F、G,连结AC交BD于O,连结OF.求证:AB=2OF.
2.5.1矩形的性质学案 P58
一、温故知新:回顾平行四边形有哪些性质?然后填空。
1、平行四边形的__________相等。表示方法:若四边形ABCD是平行四边形,则___________;
2、平行四边形的__________相等。表示方法:若四边形ABCD是平行四边形,则___________;
3、平行四边形的对角线________.表示方法: HYPERLINK "http://www.21cnjy.com" 在□ ABCD中,AC与BD相交于O,则______________
4、平行四边形的对称性:平行四边形是___对称图形,而不是______对称图形,对角线的交点是平行四边形的_________.
二、学习新知:自学P94-95页。
自学引导:①平行四边形活动框架在变化过程中,哪些量发生了变化?哪些量没有变化?从中得到哪些结论?你能试着说明结论是否成立?
②矩形的一条对角线把矩形分成两个什么三角形?矩形的两条对角线把矩形分成四个什么样的三角形?
1.矩形的定义:有一个角是直角的平行四边形,叫做矩形。由此可见,矩形是特殊的 ,它具有平行四边形的所有性质。
2.结合上面两个图形说说矩形有哪些平行四边形不具有的特殊性质?
.
3.证明:矩形的四个角都是直角
已知:如图, 图形:画在下面
求证:___________________
证明:
证明:矩形对角线相等
已知:如图, 图形:画在下面
求证:
证明:
三、探索活动
问题一 如图,矩形ABCD,对角线相交于O,观察对角线所分成的三角形,你有什么发现?
( http: / / www.21cnjy.com )
问题二 将目光锁定在Rt△ABC中,你能发现它有什么特殊的性质吗?
证明:“直角三角形斜边上的中线等于斜边的一半.”
已知: 图形:画在下面
求证:
证明:
问题三 上面结论的逆命题是: 。
是否正确?请给予证明。
四、例题学习
例:已知:如图,矩形ABCD的两条对角线相交于点O,且AC=2AB。求证:△AOB是等边三角形。(注意表达格式完整性与逻辑性)
( http: / / www.21cnjy.com )
拓展与延伸:本题若将“AC=2AB”改为“∠BOC=120°”,你能获得有关这个矩形的哪些结论?
五、练习
1、P 1
2、已知:如图,E为矩形ABCD内一点,且EB=EC。求证:EA=ED.
( http: / / www.21cnjy.com )
六、本节课你的收获是什么?
七、提高训练:1.如图,矩形纸片ABCD,且AB=6cm,宽BC=8cm,将纸片沿EF折叠,使点B与点D重合,求折痕EF的长。
( http: / / www.21cnjy.com )
2.已知矩形ABCD中,对角线交于点O,A ( http: / / www.21cnjy.com )B=6cm,BC=8cm,P是AD上一动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值是多少?这个值会随点P的移动(不与A、D重合)而改变吗?请说明理由.
( http: / / www.21cnjy.com )
3.已知:如图,矩形ABCD的两条对角线AC、BD相交于点O,∠BOC=120°,AB=4cm。求矩形对角线的长。
( http: / / www.21cnjy.com )
4.如图,在矩形ABCD中,BE平分∠ABC,交CD于点E,点F在边BC上,
如果FE⊥AE,求证FE=AE。②如果FE=AE 你能证明FE⊥AE吗?
2.5.2矩形的判定学案
一、温故知新:1.矩形是轴对称图形,它有______条对称轴.
2.在矩形ABCD中,对角线AC,BD相交于点O,若对角线AC=10cm,边BC=8cm,则△ABO的周长为________.
3.想一想:矩形有哪些性质?在这些性质中那些是平行四边形所没有的?列表进行比较.
平行四边形 矩形
边
角
对角线
二、学习新知:自学教材95—96页
1、矩形是特殊的平行四边形,怎样判定一 ( http: / / www.21cnjy.com )个平行四边形是矩形呢 请说出最基本的方法:
矩形具有平行四边形不具有的性质是:
思考:小华想要做一个矩形像框送给妈 ( http: / / www.21cnjy.com )妈做生日礼物,于是找来两根长度相等的短木条和两根长度相等的长木条制作,你有什么办法可以检测他做的是矩形像框吗?看看谁的方法可行?(得到矩形的一个判定)
2.做一做:按照画“边 ―直角、 ( http: / / www.21cnjy.com )边-直角、边-直角、边”这样四步画出一个四边形.判断它是一个矩形吗 说明理由. (探索得到矩形的另一个判定)
总结:矩形的判定方法. 矩形判定方法1:______________________________
矩形判定方法2:_______________________________
(指出:判定一个四边形是矩形,知道三个角是直角,条件就够了.因为由四边形内角和可知,这时第四个角一定是直角.)
3.议一议:下列各句判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形;( ) (2)有四个角是直角的四边形是矩形;( )
(3)四个角都相等的四边形是矩形;( ) (4)对角线相等的四边形是矩形;( )
(5)对角线相等且互相垂直的四边形是矩形;( )(6)对角线互相平分且相等的四边形是矩形;( )
(7)对角线相等,且有一个角是直角的四边形是矩形; ( )
(8)一组邻边垂直,一组对边平行且相等的四边形是矩形;( )
(9)两组对边分别平行,且对角线相等的四边形是矩形. ( )
三、例题学习。例1.:已知□ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积.
( http: / / www.21cnjy.com )
已知:如图,□ABCD的四个内角的平分线分别相交于点E、F、G、H.求证:四边形EFGH是矩形.
( http: / / www.21cnjy.com )
练习二:(选择)下列说法正确的是( ).
(A)有一组对角是直角的四边形一定是矩形(B)有一组邻角是直角的四边形一定是矩形
(C)对角线互相平分的四边形是矩形 (D)对角互补的平行四边形是矩形
2.满足下列条件( )的四边形是矩形。
A.有三个角相等 B.有一个角是直角 C.对角线相等且互相垂直 D.对角线相等且互相平分
3 .已知:如图 ,在△ABC中,∠C=90°, CD为中线,延长CD到点E,使得 DE=CD.连结AE,BE,则四边形ACBE为矩形.
( http: / / www.21cnjy.com )
4.已知:如图,在平行四边形ABCD中,E为CD中点,三角形ABE是等边三角形,求证:四边形ABCD是矩形。
( http: / / www.21cnjy.com )
四:处理教材96页练习2,102页习题2、3。
五:你学到了什么?相互说一说。
六、巩固训练:
1、在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( ).
A.测量对角线是否相互平分 B.测量两组对边是否分别相等
C.测量一组对角是否都为直角 D.测量其中三角形是否都为直角
2、能判断四边形是矩形的条件是( )
A、两条对角线互相平分 B、两条对角线相等
C、两条对角线互相平分且相等 D、两条对角线互相垂直。
3、如图,EB=EC,EA=ED,AD=BC, ∠AEB=∠DEC,证明:四边形ABCD是矩形.
( http: / / www.21cnjy.com )
4、已知四边形ABCD中AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点,求证:四边形EFGH是矩形。
5、如图,M、N分别是平行四边形ABCD对边AD、BC的中点,且AD=2AB,
求证,四边形PMQN是矩形。
( http: / / www.21cnjy.com )
2.6.1 菱形的性质学案
一、研读教材,解读目标:
1、 叫做菱形。菱形是 的平行四边形。
2、探究菱形的性质,并用模式表述菱形的特殊性质:
3、解析教材97页探究与98页例题2与练习题1、2,102页习题5、11、12
二、知识梳理
有一组邻边相等的平行四边形叫菱形.与一般平行四边形相比,菱形具有哪些性质?
定理: (菱形的边) (菱形的角)
定理: ______________ (菱形的对角线)
三、定理证明:(小组合作,先交流命题证明方法和步骤,然后自己完成证明再与组长交流)
( http: / / www.21cnjy.com )
四、典型例题
例3. 如图3个全等的菱形构成的活 ( http: / / www.21cnjy.com )动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?
五、合作交流
1.证明:菱形的面积是它两条对角线长的乘积的一半.
2.已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是菱形ABCD各边的中点,求证:OE=OF=OG=OH.
( http: / / www.21cnjy.com )
六、小结
菱形的边和对角线有不同于一般的平行四 ( http: / / www.21cnjy.com )边形的性质,有关菱形的几何计算问题可以化为_______三角形(_____三角形、等腰三角形),利用特殊三角形的性质来计算。
七、课堂练习
1.己知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为 .
( http: / / www.21cnjy.com )
2.已知四边形ABCD是菱形,O是两条对角线的交点,AC=8cm,DB=6cm,这个菱形的边长是________cm.
3.已知菱形的边长是5cm,一条对角线长为8cm,则另一条对角线长为______cm.
4.四边形ABCD是菱形,∠ABC=1 ( http: / / www.21cnjy.com )20°,AB=12cm,则∠ABD的度数为____ , ∠DAB的度数为______;对角线BD=_______,AC=_______;菱形ABCD的面积为_______.
八、目标达成训练
1.下列图形中,即是中心对称图形又是轴对称图形的是 ( )
A.等边三角形 B.菱形 C.等腰梯形 D.平行四边形
2.(09河北)如图,在菱形ABCD中,AB = 5,∠BCD = 120°,则对角线AC等于( )
A.20 B.15 C.10 D.5
3.(09南宁)如图2, ( http: / / www.21cnjy.com )将一个长为10cm,宽为8cm的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )
A.10cm2 B.20cm2 C.40cm2 D.80cm2
第3题图 第5题图 第6题图 第7题图
4.菱形的两条对角线长分别为6和8,则它的面积为________,周长为_________。
5.(09宁波)如图,菱形ABCD ( http: / / www.21cnjy.com )中,对角线AC、BD相交于点O,M、N分别是边AB、AD的中点,连接OM、ON、MN,则下列叙述正确的是( )
A.△AOM和△AON都是等边三角形 B.四边形MBON和四边形MODN都是菱形
C.四边形AMON与四边形ABCD是位似图形 D.四边形MBCO和四边形NDCO都是等腰梯形
6.(选做,09杭州)如图,在菱形ABCD中,∠A=110°,E,F
分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )
A.35° B.45° C.50° D.55°
7.(选做,07咸宁)如 ( http: / / www.21cnjy.com )图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点E,交AB于点F,F为垂足,连接DE,则∠CDE=_________
8.求证:菱形的对角线的交点到各边的距离相等。
2.6.2菱形的判定学案
一:复习:菱形有哪些特殊性质?
边:__________________________;______________________________
角:__________________________;______________________________
对角线:_____________________________;___________________________________
二、学习新知
目标一:会用菱形的定义判定一个四边形是否是菱形,并会用该种方法进行有关的证明.
(菱形的判定方法一)菱形的定义:
有 的 叫做菱形.
2.用符号语言可以表示为:
∵四边形ABCD是 四边形 ∵ ___ =____, ∴□ ABCD是菱形
3.如图在△ABC中,AD平分∠BAC交BC于D点,过D作DE∥AC交AB于E点, 过D作DF∥AB交AC于F点.
求证:(1)四边形AEDF是平行四边形 (2)∠2﹦∠3 (3)四边形AEDF是菱形
( http: / / www.21cnjy.com )
目标二:探究并掌握菱形的判定方法二
1.( 画图)自学99页最后三行的画图过程,
用圆规画出菱形ABCD,图画在右边(保留作图痕迹)
2.你发现四边形ABCD四边的关系是:
3.(猜想)四边相等的四边形ABCD是一个_____形.
4.(证明)利用上图证明:“四边相等的四边形是菱形”
已知:如上图,在四边形_______中,____=____=____=____
求证:四边形ABCD是_____.
证明:
5.(总结)由上写出菱形的判定方法二:_______ .
利用上图用符号语言表示为:在四边形ABCD中,
∵ ____=____=____=____ ∴四边形ABCD是 形
目标三:探究并掌握菱形的判定方法三
阅读99页“探究”,利用自制的学具探究菱形的判定方法并完成下面各题
1.由“在一长一短的木条中点处固定一个小钉”可知: = , =
∴四边形ABCD是 四边形
2.转动十字,当∠_____= °时即___ ⊥ ___时,四边形变成了菱形.
3. (猜想)对角线互相____ 的平行四边形是菱形.
4.请利用下图证明你的猜想:
已知:如图,在□ABCD中,AC和BD是对角线,并且AC⊥BD于点O,求证:□ABCD是菱形.
( http: / / www.21cnjy.com )
5.总结写出菱形判定方法三:
利用上图用符号语言可以表示为:∵四边形ABCD是平行四边形,∵AC___BD,∴□ABCD是菱形
目标四:利用菱形判定方法进行计算和证明
1.自学99页例三完成下题“在□ABCD中,对角线AC和BD相交于点O,并且AB=9,OB=6,OA=3 HYPERLINK "http://www.21cnjy.com" .求证:(1)AC⊥BD (2)□ABCD是菱形吗?说说你的理由. (3)求四边形ABCD的面积.
( http: / / www.21cnjy.com )
2.判断题,对的画“√”错的画“×”
(1).对角线互相垂直的四边形是菱形( )
(2).一条对角线垂直另一条对角线的四边形是菱形( )
(3)..对角线互相垂直且平分的四边形是菱形( )
(4).对角线相等的四边形是菱形( )
三、小结:菱形的常用判定方法
四:拓展延伸
1.如图,两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是菱形吗?
求证:(1)四边形ABCD是平行四边形
(2) 过A作AE⊥BC于E点, 过A作AF⊥CD于F.用等积法说明BC=CD.
(3) 求证:四边形ABCD是菱形.
( http: / / www.21cnjy.com )
2.已知:如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形。
( http: / / www.21cnjy.com )
3. 如图,AC⊥BC,AE平分∠CAB,CD⊥AB,EF⊥AB,连接FG,求证:CEFG为菱形.
( http: / / www.21cnjy.com )
2.7正方形学案1
一.温故知新 填表:
性质 判定方法
矩形 边:角:对角线:对称性: 1.2.3.
菱形 边:角对角线:对称性: 1.2.3.
二.学习新知
自学教材100-101页,落实:
性质 判定方法
正方形 边:角对角线:对称性:
自学例4,并在学案上做一遍:
完成课本P101页练习1、2、3题
三.释疑提高
1.正方形的四条边____ __,四个角___ ____,两条对角线____ ____.
2.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD B. AD∥BC,∠A=∠C
C. AO=BO=CO=DO,AC⊥BD D. AO=CO,BO=DO,AB=BC
3.如图,正方形ABCD中,对角线 ( http: / / www.21cnjy.com )交于O,E是OB上一点,DG⊥AE于G,DG交OA于F.①求证:OE=OF. ②当E为OB延长线上一点时,画出对应的图形,观察①中结论是否仍然成立,并给予证明.
( http: / / www.21cnjy.com )
4.如图,正方形ABCD中,E、 ( http: / / www.21cnjy.com )F为BC、CD上两点,且∠EAF=45°,①求证:EF=BE+DF. ②以上命题的逆命题是否成立?③若AB=12,求△CEF周长.④若AB=12,EF=10,求△AEF面积.
( http: / / www.21cnjy.com )
四、小结归纳
五、巩固检测1.课本102页习题7、13、15; 2.作业精编19.2.3 正方形
2.7 正方形学案2
一、温故知新
1.有一组邻边____ __,且有一个角____ __的平行四边形是正方形。
2.正方形的四边____ __,四角____ __,对角线____ __且____ __;正方形既是矩形,又是____ _;既是轴对称图形,又是____ ______ __。
3.如图正方形ABCD的边长为8,DM=2,N为AC上一点,则DN+MN的最小值为 .
4.如图,正方形ABCD边长为2,两对角线交点为O,OEFG也为正方形,则图中阴影部分面积为 .
5.如图,若四边形ABCD是正方形,△CDE是等边三角形,则∠EAB的度数为 .
6. 如图,已知正方形AB ( http: / / www.21cnjy.com )CD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF的面积为200,则BE的值是 .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
二、学习新知
作业精编73页例1、例2(独立写出过程)
三、释疑提高
1.如图,正方形ABCD中,E为BC上一点,AF平分∠DAE,求证:BE+DF=AE.
( http: / / www.21cnjy.com )
2. 如图,正方形ABCD中,E为BC上一点,DF=CF,DC+CE =AE,求证:AF平分∠DAE.
( http: / / www.21cnjy.com )
3.如图,BF平行于正方形ADCD的对角线AC,点E在BF上,且AE=AC,CF∥AE,求∠BCF.
( http: / / www.21cnjy.com )
四、小结归纳
五、巩固检测:课堂作业P74和学法大视野
3.1 平面直角坐标系
◆回顾探索
1.平面直角坐标系:在平面上画 ( http: / / www.21cnjy.com )出两条原点重合,互相垂直且具有相同的_____的数轴,就叫建立平面直角坐标系,其中水平的一条数轴叫做______轴或______轴,取向_______为正方向,垂直的数轴叫_______轴或_______轴,取向_______为正方向.
2.对称点、特殊点的坐标的特征:(1)关于x轴对称的点的坐标,______相等,_____相反;
(2)关于y轴对称的点的坐标,________相等,_________相反.
(3)关于原点对称的点的坐标特征是____________.
(4)x轴上的点的坐标特征是:_________,y轴上的点的坐标特征是________.
◆课堂测控
测试点1 平面直角坐标系
1.如图,是象棋盘的一部分,若位于点(1,-2)上,位于点(3,-2)上,则位于点( )上.
A.(-1,1) B.(-1,2) C.(-2,1) D.(-2,2)
2.观察下列图象,与图①中的鱼相比,图②中的 ( http: / / www.21cnjy.com )鱼发生了一些变化,若图①中鱼上点P的坐标为(5,4),则这个点在图②中的对应点P1的坐标应为________.
( http: / / www.21cnjy.com )
① ②
3.(体验探究题)如图,A表示三经路与一纬路的十字路口,B表示一经路与三纬路的十字路口,如果用(3,1)→(3,2)→(3,3)→(2,3)→(1,3)表示由A到B的一条路线,用同样的方式写出另外一条由A到B的路径.
(3,1)→(_____)→(_____)→(_____)→(1,3)
测试点2 对称点、特殊点的坐标的特征
4.在平面直角坐标系中,点P(-1,4)关于原点的对称点是在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.在平面直角坐标系中,下列各点在第四象限的是( )
A.(2,1) B.(2,-1) C.(-2,1) D.(-2,-1)
6.已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′C′与△ABC关于y轴对称,则点A的对应点A′的坐标为( )
A.(-4,2) B.(-4,-2)
C.(4,-2) D.(4,2)
◆课后测控
1.在平面直角坐标系中,点P(-2,3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2006,河北)在平面直角坐标系中,若点P(x-2,x)在第二象限,则x的取值范围为( )
A.00 D.x>2
3.若点P(a,b)在第四象限,则点Q(-a,b-1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.点M(2,-3)关于y轴的对称点N的坐标是( )
A.(-2,-3) B.(-2,3) C.(2,3) D.(-3,2)
5.在直角坐标系中,如图所示,右边的图案是左边的图案经过平移得到,左图中左右眼睛的坐标分别是(-4,2),(-2,2),右边图形中左眼的坐标是(3,4),则右图案中右眼的坐标是_______.
6.在平面直角坐标系中,点P(-2,3)关于原点的对称点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
7.根据指令[S,A](S≥0.0° ( http: / / www.21cnjy.com )(1)若给机器人下了一个指令[4,60°],则机器人应移动到点_______;
(2)请你给机器人下一个指令_________,使其移动到点(-5,5).
8.已知a是整数,点A(2a+1,2+a)在第二象限,则a=_______.
9.如图所示在直角坐标系中,射线Ox绕原点O逆时针旋转330°到OA的位置,若OP=2,则点P的坐标为_______.
10.已知△ABC的顶点坐标分别为:A(-7,0),B(1,0),C(-3,4),求△ABC的面积.
◆拓展创新
如图,我们给中国 ( http: / / www.21cnjy.com )象棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
(1)写出下一步“马”可能到达的点的坐标_______;
(2)顺次连接(1)中的所有点,得到的图形是_______图形(填“中心对称”、“旋转对称”、“轴对称”);
(3)指出(1)中关于点P成中心对称的点_________.
3.3图形与坐标
一、选择题
1.下列各点,在第二象限内的是 ( )
A.(-1,0) B.(2,2) C.(-2,3) D.(-2,-3)
2.已知点P的坐标为 (-2,0),则下列说法正确的是 ( )
A.点P在x轴上 B.点P在y轴上 C.点P在第一象限 D.点P在第三象限
3.如果点P(m + 3,m + 1)在x轴上,则点P坐标为 ( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
4.与直角坐标平面内的点对应的坐标是( )
A.一对实数 B.一对有序实数 C.一对有理数 D.一对有序有理数
5.在平面直角坐标系中,点P(-1,1)关于x轴的对称点在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.若点P(x, y) 在第二象限,且到x轴的距离为3,到y轴的距离为2,则点P坐标为 ( )
A. (2, 3) B.(-2, 3) C.(2, -3) D.( 3, -2)
7. 电影票上“6排3号”,记作(6,3),则8排6号记作( )毛
A.(6,3) B.(6,8) C.(8,3) D.(8,6)
二、填空题
8.若点P (-3, a)在第二象限角平分线上,则a = .
9.已知矩形ABCD三个顶点的坐标A (-1, -1),B (-1, 1),
C (2, 1),点D的坐标是 .
10.点A在(-3,2) ( http: / / www.21cnjy.com )在平面直角坐标系中向右平移5个单位得到点B,则点B的坐标为________,点B关于x轴的对称点的坐标为________,点B关于y轴的对称点的坐标为___________.
11.点M(-2,3)到x轴的距离为_______,到y轴的距离为______.
三、解答题
12.如图,点A表示2街与4大道的十 ( http: / / www.21cnjy.com )字路口,点B表示4街与2大道的十字路口, 如果用(2,4)→(2,3)→(3,3)→(4,3)→(4,2)表示A到B的途径, 请你用同样的方法尽可能多地表示A到B的其它途径.
13.四边形OABC在平面直角坐标系中的位置如图所示:
⑴写出右图中四边形OABC各顶点的
坐标;
⑵线段BC与横坐标、纵坐标有什么特殊的位置关系?
⑶四边形OABC是什么特殊四边形?
14.在下图中找出下列各点,并将
各点用线段首尾顺次连结起来,观察所得的图形,你觉得它像什么?
(1,1),(3,4),(3,3),(7,3),(8,2),(8,0),(7,1),(4,1),(3,0),(3,1)
15.如下图所示,已知 ( http: / / www.21cnjy.com )OABC在平面直角坐标系中三顶点的坐标分别为O(0,0),A(4,2),B(0,3),另一顶点C未标出,试根据已知三点确定点C的坐标,并画出平行四边形.
16:已知△ABC 在直角坐标系中的位 ( http: / / www.21cnjy.com )置如图4所示,如果△A'B'C' 与△ABC 关于y轴对称,那么点A的对应点A'的坐标为( ). A.(-4,2) B.(-4,-2) C.(4,-2) D.(4,2)
【基础概念】
1、平面上物体的位置可以用有序实数对来确定。
2、在平面内确定物体的位置一般需要几个数据 有哪些方法
(1)用有序数对来确定;
(2)用方向和距离(方位)来确定;
3、在平面内有公共原点而且互相垂直的两条数轴,就构成了平面直角坐标系。简称直角坐标系,坐标系所在的平面就叫做坐标平面
4、掌握各象限上及x轴,y轴上点的坐标的 特点:
第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-)
5、x轴上的点纵坐标为0,表示为(x,0);y轴上的点横坐标为0,表示为(0,y)
6、(1)关于x轴对称的两点:横坐标相同,纵坐标互为相反数。
(2)关于y轴对称的两点:纵坐标相同,横坐标互为相反数。
(3)关于原点对称的两点:横坐标互为相反数,纵坐标互为相反数。
§3.3 轴对称和平移的坐标表示
学习目标:1、掌握点平移得到新坐标的规律,并且熟练画出图形。
2、理解“数形结合”;体会坐标系中图形平移的实际应用。
学习重点:探究点或图形平移引起的的坐标的变化规律。
学习难点:如何正确理解图形在坐标系中的平移变换。
☆ 自主学习 ☆
一、链接:
在平面直角坐标系中,描出下列各点,并将
各点用线段依次连接起来:
(1,1) (2,3) (3,1) (4,3) (5,1)
观察得到的图形,你觉得它像什么?
二、导读:预习课本,完成以下题目:
如图,按下列要求在直角坐标系中标出点。
(1)将点A(-1,-2)向右平移5个单位
长度得到A1点的坐标为 。
(2)将点A(-1,-2)向左平移2个单位
长度得到A2点的坐标为 。
(3)将点A(-1,-2)向上平移4个单位
长度得到A3点的坐标为 。
(4)将点A(-1,-2)向下平移1个单位
长度得到A4点的坐标为
总结:坐标系中,点的上下平移,只改变它的___坐标;点的左右平移,只改变它的___坐标;
三、预习反思:通过预习,你还有哪些疑惑呢 请将它写下来,你准备怎样解决
☆ 合作探究 ☆
1、思考一下坐标系中点的平移与坐标变化之间的关系,试填空:
(1)点的横坐标每增加1个单位,那么这个点将向___移动1个单位。
(2)点的横坐标每减少1个单位,那么这个点将向___移动1个单位。
(3)点的纵坐标每增加1个单位,那么这个点将向___移动1个单位。
(4)点的纵坐标每减少1个单位,那么这个点将向___移动1个单位。
(5)已知点P(-3,5),如果把它向上平移6个单位,再向左平移4个单位,得到点Q,则Q点的坐标是__________。
2、如图:铅笔图案的五个顶点的坐标分别
是(0,1)(4,1)(5,1.5)(4,2)
(0,2),将图案向下平移2个单位长度,
作出相应图案,并写出平移后相应5点
的坐标。
3、从上题你发现点向左(或右),向上(或下)移动的规律了吗?试填空:
(1)将点(x,y)向右平移a个单位长度,可得对应点( , )。
(2)将点(x,y)向左平移a个单位长度,可得对应点( , )。
(3)将点(x,y)向上平移a个单位长度,可得对应点( , )。
(4)将点(x,y)向下平移a个单位长度,可得对应点( , )。
☆ 归纳反思 ☆
把平面直角坐标系中的一个图形,按下面的要求平移,那么图形上任一点的坐标(x,y)是如何变化的
①向左或向右移动a(a>0)个单位。
②向上或向下移动b(b>0)个单位。
③向左或向右移动a个单位,再向上或向下移动b个单位。
☆ 达标检测 ☆
1、如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是( )
(A)(2,-2),(3,4),(1,7)。
(B)(-2,2),(4,3),(1,7)。
(C)(-2,2),(3,4),(1,7)。
(D)(2,-2),(3,4),(2,6)。
2、在坐标系中,点P先向左平移4个单位,再向上平移2个单位后的坐标为(-1,0),则P点的坐标是_________。
3、已知三角形的三个顶点都在以下表格的交点上,其中A(3,3)、B(3,5),请在表格中
确定点C的位置,使 ( http: / / www.21cnjy.com )=2,这样的点C有多少个?请分别表示出来。
中学八年级上数学第四章函数导学案(1)
4.1.1变量与函数
学习目标:1、通过探索具体问题中的数量关系和变化规律来了解常量、变量的意义;
2、学会用含一个变量的代数式表示另一个变量;
学习重点:了解常量与变量的意义; 学习疑点:较复杂问题中常量与变量的识别
学习过程:
揭示目标,学法指导
问题一:汽车以60千米/小时的速度匀速行驶,行驶里程为s千米,行驶时间为t小时.
1.请同学们根据题意填写下表:
t/时 1 2 3 4 5 t
s/千米
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含t的式子表示s: s=________,t的取值范围是 _________ .
这个问题反映了匀速行驶的汽车所行驶的路程____随行驶时间___的变化过程.
二、学生探究,教师巡导
(一)问题探究:
问题二:1.电影院播放的电影《爸爸去哪儿》票价20元/张,请同学们根据题意填写下表:
售出票数(张) 早场150 午场206 晚场310 x
收入y (元)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含x的式子表示y: y=______ ,x的取值范围是 .
这个问题反映了票房收入_________随售票张数_________的变化过程.
问题三:弹簧伸长量为0.16m/kg,完成下列问题
1.请同学们根据题意填写下表:
所挂重物(kg) 1 2 3 4 5 m
受力后的弹簧长度L(cm)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含m的式子表示L: L=____________ ,m的取值范围是 .
这个问题反映了_________随_________的变化过程.
问题四:1.请同学们根据题意填写下表:(用含 ( http: / / www.21cnjy.com )的式子表示)
圆面积s(cm2) 10 20 30 s
半径r(cm)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含s的式子表示r.r=_________,s的取值范围是 .
这个问题反映了___ _ 随_ __的变化过程.
问题五:请看书第110页问题2,完成下列问题
1.请同学们根据题意填写下表:
长x(m) 1 2 3 4 x
正方形面积s(m2)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含x的式子表示s. S=__________________,x的取值范围是 .
这个问题反映了矩形的___ _ 随_ __的变化过程.
小结:以上这些问题都反映了不同事物的变化 ( http: / / www.21cnjy.com )过程,其实现实生活中还有好多类似的问题,在这些变化过程中,有些量的值是按照某种规律变化的,有些量的数值是始终不变的。
(二)得出结论: 在一个变化过程中,我们称数值发生变化的量为________;
在一个变化过程中,我们称数值始终不变的量为________;
三、学生展示,老师精导
学生展示以上探究的问题,老师强调“变化过程”,“变量”,“常量”的意义。
四、边练边清,巩固提升
1.齿轮每分钟120转,如果 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。表示转数,表示转动时间,那么用 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。表示的关系是 ,其中 为变量, 为常量.
2.摄氏温度C与华氏温度F之间的对应关系为 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。℃,则其中的变量是 ,常量是 。
3.在⊿中,它的底边是 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。,底边上的高是,则三角形的面积 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。,当底边的长一定时,在关系式中的常量是 ,变量是 。
4.在圆的周长 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。中,常量与变量分别是( )
(A) 2是常量,c、、 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。是变量 (B)2是常量,c、 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。是变量
(C) c、2是常量,是变量 (D)2是常量,c、 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。是变量
5.小军用50元钱去买单价是8元的笔记本,则他剩余的钱Q(元)与他买这种笔记本的本数x之间的关系是 ( )
A.Q=8x B.Q=8x-50 C.Q=50-8x D.Q=8x+50
6.甲、乙两地相距S千米,某人行完全程 ( http: / / www.21cnjy.com )所用的时间t(时)与他的速度v(千米/时)满足vt=S,在这个变化过程中,下列判断中错误的是 ( )
A.S是变量 B.t是变量 C.v是变量 D.S是常量
课后反思:
你有什么收获?
4.1.2函数的表示法
学习目标:
(1)理解函数的概念,能准确识别出函数关系中的自变量和函数
(2)会用变化的量描述事物;(3)会用运动的观点观察事物,分析事物X|k |b| 1 . c|o |m
学习重点:函数的概念 学习难点:认识函数,领会函数的意义
学习过程:
揭示目标,学法指导:
1、请你举出生活中含有两个变量的变化过程,说明其中的常量和变量。
二、学生探究,教师巡导
请看书112——117页内容,完成下列问题:
思考书中第112页的说一说,归纳出变量之间的关系。
完成书上第113页的动脑筋,体会图形中体现的变量和变量之间的关系。
归纳出函数的定义,明确函数定义中必须要满足的条件。
归纳:一般的,在一个变化过程中,如果有___ ( http: / / www.21cnjy.com )___变量x和y,并且对于x的_______,y都有_________与其对应,那么我们就说x是__________,y是x的________。如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值。
三、学生展示,老师精导
1函数的定义:
必须是一个变化过程;
两个变量;
其中一个变量每取一个值 ,另一个变量有且有唯一值对它对应。
2、学生展示
例1:一辆汽车的油箱中现有汽油 ( http: / / www.21cnjy.com )50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:千米)的增加而减少,平均耗油量为0.1L/千米。
(1)写出表示y与x的函数关系式.
(2)指出自变量x的取值范围.
(3) 汽车行驶200千米时,油箱中还有多少汽油?
教师精导:函数自变量的取值范围与问题的实际意义。
四、边练边清,巩固提升
P106页:1,2题
1、判断下列变量之间是不是函数关系:
(1)长方形的宽一定时,其长与面积;
(2)等腰三角形的底边长与面积;
(3)某人的年龄与身高;
2.写出下列函数的解析式.
(1)一个长方体盒子高3cm,底面是正方形,这个长方体的体积为y(cm3),底面边长为x(cm),写出表示y与x的函数关系的式子.
(2)汽车加油时,加油枪的流量为10L/min.
①如果加油前,油箱里还有5 L油,写出在加油过程中,油箱中的油量y(L)与加油时间x(min)之间的函数关系;
②如果加油时,油箱是空的,写出在加油过程中,油箱中的油量y(L)与加油时间x(min) 之间的函数关系.
3.(2007.云南)某地在调整电 ( http: / / www.21cnjy.com )价时,为了鼓励居民节约用电,采取了居民用电分段计价的办法:若每月每户用电量不超过80度,按0.48元/ 度收费;用电量在80~180度(含180度)之间,超过80度的部分按0.56元/度收费;用电量在180度以上,超过180度的部分按0.62元/度收费.同时规定在实行调价的当月收费中,用电量的1/3按原电价0.42元/度收费,用电量的2/3按调价后的分段计价办法收费.以后各月的用电量全部按分段计价的办法收费.
课后反思:
你的收获:
你的疑问:
函数及其图象(3)
学习目标:1.知道函数图象的意义;2.能画出简单函数的图象,会列表、描点、连线;
3.能从图象上由自变量的值求出对应的函数的近似值。
学习重点:1.函数图像的画法;2.观察分析函数图像 学习疑点:分析概括图像中的信息
学习过程:
一、揭示目标,学法指导
1.什么是函数图像
2.如何作函数图像?具体步骤有哪些?
3.如何判定一个图像是函数图像,你判断的依据是什么
4.有哪些方法表示函数关系?各自的优缺点是什么?
二、学生探究,教师巡导
1.如图1是某地区一天的气温随时间变化的图象,根据图象回答:在这一天中:
(1)气温(℃) (填“是”或“不是”)时间(时)的函数.(2) 时气温最高, 时气温最低,最高汽温是 ℃,最低气温是 ℃.(3)10时的气温是 ℃.(4) ___时气温是4℃.(5) 时间内,气温不断上升.(6) 时间内,气温持续不变.
2等腰△ABC的周长为10cm,底边BC的长为ycm,腰AB的长为xcm.
(1)写出y关于x的函数关系式 (2)求x的取值范围
(3)求y的取值范围 (4)画出函数的图象
三、学生展示,老师精导
正确理解函数图象与实际问题间的内在联系
函数的图象是由一系列的( )组成,图象上每一点的坐标(x,y)代表了该函数关系的一对对应值。
1、读懂横、纵坐标分别所代表的实际意义;2、读懂两个量在变化过程中的相互关系及其变化规律。
这三种表示函数的方法各有优缺点。
1.用解析法表示函数关系 优点:简单明了。 ( http: / / www.21cnjy.com )能从解析式清楚看到两个( )之间的全部相依关系,并且适合进行理论分析和推导计算。缺点:在求对应值时,有时要做较复杂的计算。
2.用列表表示函数关系
优点:对于表中( )的每一个值,可以不 ( http: / / www.21cnjy.com )通过计算,直接把函数值找到,查询时很方便。缺点:表中不能把所有的自变量与函数对应值全部列出,而且从表中看不出变量间的对应规律。
3.用图象法表示函数关系
优点:形象直观,可以形象地反映出( )的趋势和某些性质,把抽象的函数概念形象化。缺点:从自变量的值常常难以找到对应的函数的准确值。
函数的三种基本表示方法,各有各 ( http: / / www.21cnjy.com )的优点和缺点,因此,要根据不同问题与需要,灵活地采用不同的方法。在数学或其他科学研究与应用上,有时把这三种方法结合起来使用,即由已知的函数解析式,列出自变量与对应的函数值的表格,再画出它的图象。
四、边练边清,巩固提升
1.若点p在第二象限,且p点到x轴的距离为,到y轴的距离为1,则p点的坐标是( )
A.(-1, HYPERLINK "http://www.21cnjy.com" ) B.(- HYPERLINK "http://www.21cnjy.com" ,1) C.( HYPERLINK "http://www.21cnjy.com" ,-1) D.(1,- HYPERLINK "http://www.21cnjy.com" )
2.下列函数中,自变量取值范围选取错误的是( )
A. HYPERLINK "http://www.21cnjy.com" 中,x取全体实数 B. HYPERLINK "http://www.21cnjy.com" 中, HYPERLINK "http://www.21cnjy.com" C. HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" D. HYPERLINK "http://www.21cnjy.com" 中, HYPERLINK "http://www.21cnjy.com"
3.(常州市,2000)小明的父亲饭后出去散 ( http: / / www.21c
年
湘
教
版
数
学
八
年
级
下
册
导
学
案
学习目标:
1.了解直角三角形的判定定理和性质定理
2.会用定理解决有关问题
知识链接
1.三角形内角和是________,
2.若∠A=36°,则它的余角∠B=_______
3.画出AB边上的中线
自主探究
阅读课本第2至3页内容,并自主探究下列几个问题:
1.在△ABC中,如果∠A+∠B=90°,则∠C=____。
于是△ABC是__________.
由上可得:有两个角_______的三角形是直角三角形
2.如图,Rt△ABC中,CD是斜边AB上的中线,
(l)量一量斜边AB的长度=__________
(2)量一量斜边上的中线CD的长度=________
(3)于是有CD=__AB
由此可得:直角三角形斜边上的中线等于斜边的________
合作交流
根据以上探究过程,请你与小组成员一起交流,解决下列问题:
1.在△ABC中,∠ACB=90°CD⊥ ( http: / / www.21cnjy.com )AB,那么与∠B互余的角有______,_______, 与∠B相等的角有___________。
2. 如图,Rt△ABC中,CD是斜边AB上的中线,AB=8cm,
则 AD=____cm, BD=_____cm, CD=________cm
3.如图,CD是△ABC的中线,∠ACB=90°,∠CDB=110°,则∠A=__________
实践应用
已知,如图,CD是△ABC的AB边上的中线,CD= 1/2 AB,求证:△ABC是直角三角形
自主检测
1.在△ABC中,若∠A=25°,∠B=65°,此三角形为________三角形
2.直角三角形中,两锐角的平分线相交所成的角的度数是_________。
3.若∠A:∠B:∠C=2:3:5,则△ABC是_________三角形
4.已知,△ABC中,AB=AC,AD平分 ( http: / / www.21cnjy.com )∠BAC,点E为AC的中点,请你写一个正确的结论.________________________________
5.如图,AC∥BD, ∠A和∠B的平分线的平分线相交于E,则∠AEB等于多少度?为什么?
小结:今天我们学了什么?你还有什么疑惑吗?
导学内容:1 进一步掌握直角三角形的性质----直角三角形中,30度的角所对的边等于斜边的一半;
2 能利用直角三角形的性质解决一些实际问题。
导学重点:直角三角形的性质 导学难点:直角三角形性质的应用
导 学 程 序
导入新课
1.直角三角形有哪些性质?
2 按要求画图:
(1)画∠MON,使∠MON=30°,
(2)在OM上任意取点P,过P作ON的垂线PK,垂足为K,量一量PO,PK的长度,PO,PK有什么关系?
(3) 在OM上再取点Q,R,分别过Q,R ( http: / / www.21cnjy.com )作ON的垂线QD,RE,垂足分别为D,E,量一量QD,OQ,它们有什么关系?量一量RE,OR,它们有什么关系?
由此你发现了什么规律?
直角三角形中,如果有一个锐角等于 ,那么它所对的 等于 .
合作交流,探究新知
1 探究直角三角形中,如果有一个锐角等于30°,那么它所对的直角边为什么等于斜边的一半。如图,Rt△ABC中,∠A=30°,BC为什么会等于 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 AB?(提示:取AB的中点D,连结CD)
证明:取AB的中点D,连结CD则AD=BD
因为 CD为Rt△ABC斜边的中线
所以
又因为 ∠A=30°所以∠B=
所以 △CDB为 三角形
所以 BC=
所以 BC=
得出结论:
2 上面定理的逆定理:上面 ( http: / / www.21cnjy.com )问题中,把条件“∠A=30°”与结论“BC=1/2AB”交换,结论还成立吗?(证明过程讨论完成)得出结论:
三、巩固练习
1 几何中的运用
(1)在△ABC中,△C=90°,∠B=15°,DE垂直平分AB,垂足为点E,交BC边于点D,BD=16cm,则AC的长为______
(2)如图在△ABC中,若∠BAC=120°,AB=AC,AD⊥AC于点A,BD=3,则BC=______.
(3)在A岛周围20海里水域有暗礁,一轮船由西向东航行到O处时,发现A岛在北偏东60°的方向,且与轮船相距30 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 海里,该轮船如果不改变航向,有触礁的危险吗?
四、小结今天我们学习哪些内容?
1.直角三角形的性质:
2.直角三角形的判定:
直角三角形的性质和判定3
一、知识要点
1、直角三角形的性质:
(1)在直角三角形中,两锐角 ;
(2)在直角三角形中,斜边上的中线等于__________的一半;
(3)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于 ___________;
(4)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于___________。
2、 直角三角形的判定:
(1)有一个角等于_________的三角形是直角三角形;
(2)有两个角_____________的三角形是直角三角形;
(3)如果三角形一边上的中线等于这条边的________,那么这个三角形是直角三角形。
二、知识运用典型例题
例1、在△ABC中,∠C=90°,∠A=30°, CD⊥AB,
(1) 若BD=8,求AB的长;
(2) 若AB=8,求BD的长。
例2、如图,在Rt△ABC中,CD是斜边上的中线,CE⊥AB,已知AB=10cm,DE=2.5cm,求CD和∠DCE。
例3、如图,在△ABC中,∠C=90°,∠A= HYPERLINK "http://www.21cnjy.com" °,∠B=2 HYPERLINK "http://www.21cnjy.com" °求 HYPERLINK "http://www.21cnjy.com" 。
例4、如图,已知AB⊥BC,AE∥BC,∠1=45°,∠E=70°.求∠2,∠3,∠4的度数.
例5、如图,在△ABC中,∠ACB=90°, ∠A=15°,AB=8cm,CD为AB的中线,求△ABC的面积。
例6、如图,在△ABC中,∠ACB=90°,AD=AC,BE=BC,求∠DCE的度数。
三、知识运用课堂训练
在Rt△ABC中,∠C=90°,AB=2cm,AC=BC,CD⊥AB于D点,则CD=_______cm;
如果三角形的两条边上的垂直平分线的交点在第三条边上,那么这个三角形是( )
A.锐角三角形 B.等腰三角形
C.直角三角形 D.钝角三角形
3、已知三角形的的三个内角的度数之比为1:2:3,它的最大边长为6cm,那么它的最小边长为_________cm;
4、直角三角形中一个锐角为30°,斜边和较小的边的和为12cm,则斜边长为_____________;
5、如图,在△ABC中,∠ACB=90°,D是AB的中点,CD=4cm,∠B=30°,
则AC=_____cm
6、将一张长方形纸片ABCD如图所示折叠,使顶点C落在C′点. 已知AB=2,∠DEC′=30°,则折痕DE的长为( )
A 、2 B、 HYPERLINK "http://www.21cnjy.com" C、4 D、1
知识运用课后训练
1、下列命题错误的是( )
A.有两个角互余的三角形一定是直角三角形;
B.在三角形中,若一边等于另一边的一半,则较小边的对角为30°;
C.直角三角形斜边上的中线等于斜边的一半;
D.△ABC中,若∠A:∠B:∠C=1:4:5,则这个三角形为直角三角形。
2、已知在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=4cm,则BC=_______cm,
∠BCD=_______,BD=_______cm,AD=________cm;
3、已知三角形的的三个内角的度数之比为1:2:3,且最短边是3厘米,则最长边上的中线等于____________;
在△ABC中,∠C=90°,∠A、∠B的平分线相交于O,则∠AOB=_________;
5、在△ABC中,∠BAC=90°,AC=5cm,AD是高,AE是斜边上的中线,且DC=1/2AC,求∠B 的度数及AE的长。
你在学习中还有什么没有弄懂的问题吗?
课题:直角三角形的性质和判定2第4课时
教学目标 1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。2.培养在实际生活中发现问题总结规律的意识和能力。
教学重点:勾股定理的内容及证明。
教学难点:勾股定理的内容及证明。
引直角△ABC的主要性质是:∠C=90°(用几何语言表示)(1)两锐角之间的关系: (2)若D为斜边中点,则斜边中线 (3)若∠B=30°,则∠B的对边和斜边: 二.探 自学内容:1、阅读教材P9至P11页;2、完成自主学习;3、并找出你存在的疑难,并用红笔标记。 (一)、1、(1)、同学们画一个直角边为3cm和4cm的直角△ABC,用 刻度尺量出AB的长。(2)、再画一个两直角边为5和12的直角△ABC,用刻度尺量AB的长 问题:你是否发现32+42与52,52+12和132的关系,即32+42 52,52+12 132,2、完成10页的探究,补充下表,你能发现正方形A、B、C的关系吗?A的面积(单位面积)B的面积(单位面积)C的面积(单位面积)图1图2由此我们可以得出什么结论?可猜想:命题1:如果直角三角形的两直角边分别为a、b,斜边为c,那么 。(二)、勾股定理的证明1、已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。求证:a2+b2=c2证明:4S△+S小正=S大正=根据的等量关系:由此我们得出:勾股定理的内容是: 。三.小结 四.用1、在Rt△ABC中, HYPERLINK "http://www.21cnjy.com" ,(1)如果a=3,b=4,则c=________;(2)如果a=6,b=8,则c=________;(3)如果a=5,b=12,则c=________;(4) 如果a=15,b=20,则c=________. 2、下列说法正确的是( )A.若 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 是△ABC的三边,则 a2+b2=c2B.若 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 是Rt△ABC的三边,则 a2+b2=c2C.若 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 是Rt△ABC的三边, HYPERLINK "http://www.21cnjy.com" , 则 a2+b2=c2D.若 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 是Rt△ABC的三边, HYPERLINK "http://www.21cnjy.com" ,则 a2+b2=c23、一个直角三角形中,两直角边长分别为3和4,下列说法正确的是( )A.斜边长为25 B.三角形周长为25 C.斜边长为5 D.三角形面积为204、如图,三个正方形中的两个的面积S1=25,S2=144,则另一个的面积S3为________.
课题:勾股定理综合应用
教学目标 1.会用勾股定理解决较综合的问题。2.树立数形结合的思想。
教学重点:勾股定理的综合应用。
教学难点:勾股定理的综合应用。。
引 复习勾股定理的内容。二.探 ( http: / / www.21cnjy.com )1.△ABC中,AB=AC=25cm,高AD=20cm,则BC= ,S△ABC= 。2.△ABC中,若∠A=1/2∠B=1 ( http: / / www.21cnjy.com )/2∠C,AC=10 cm,则∠A= 度,∠B= 度,∠C= 度,BC= ,S△ABC= 。例1:已知:在Rt△ABC中,∠C=90°,CD⊥BC于D,∠A=60°,CD= HYPERLINK "http://www.21cnjy.com" ,求线段AB的长。解答过程:例2:已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。解答过程:三.结 小结:不规则 ( http: / / www.21cnjy.com )图形的面积,可转化为特殊图形求解,本题通过将图形转化为直角三角形的方法,把四边形面积转化为三角形面积之差。四.用1. 如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC中,边长为无理数的边数是( )A. 0 B. 1 C. 2 D. 32. 如图所示,在△ABC中,三边a,b,c的大小关系是( )A.a<b<c B. c<a<b C. c<b<a D. b<a<c3.等边△ABC的高为3cm,以AB为边的正方形面积为 .4.如图,所有的四边形都是正方形, ( http: / / www.21cnjy.com )所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为_______cm25.若△ABC中,AB=13,AC=15,高AD=12,则BC的长是 .6.如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是 ;
课题:勾股定理逆定理
教学目标 1.体会勾股定理的逆定理得出过程,掌握勾股定理的逆定理。2.探究勾股定理的逆定理的证明方法。3.理解原命题、逆命题、逆定理的概念及关系。
教学重点:掌握勾股定理的逆定理及证明
教学难点:掌握勾股定理的逆定理
引问题一:1、怎样判 ( http: / / www.21cnjy.com )定一个三角形是直角三角形?2、下面的三组数分别是一个三角形的三边长a.b.c5、12、13 7、24、25 8、15、17(1)这三组数满足 a2+b2=c2吗?(2)分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?猜想命题2:如果三角形的三边长 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" ,满足 a2+b2=c2,那么这个三角形是 三角形问题二:命题1: 命题2: 命题1和命题2的 和 正好相反,把像这样的两个命题叫做 命题,如果把其中一个叫做 ,那么另一个叫做 二.探 自学内容:1、阅读教材P14至P15页;2、完成自主学习;3、并找出你存在的疑难,并用红笔标记。 例1 说出下列命题的逆命题,这些命题的逆命题成立吗?⑴同旁内角互补,两条直线平行。⑵如果两个实数的平方相等,那么两个实数平方相等。⑶线段垂直平分线上的点到线段两端点的距离相等。⑷直角三角形中30°角所对的直角边等于斜边的一半。例2 已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,a=n2-1,b=2n c= n2+1(n>1)求证:∠C=90°。三.结 师生小结勾股定理逆定理四.用1.判断题。⑴在一个三角形中,如果一边上的中线等于这条边的一半,那么这条边所对的角是直角。( ) ⑵命题:“在一个三角形中,有一个角是30°,那么它所对的边是另一边的一半。”的逆命题是真命题。( )⑶勾股定理的逆定理是:如果两条直角边的平方和等于斜边的平方,那么这个三角形是直角三角形。( )⑷△ABC的三边之比是1:1:√2 ,则△ABC是直角三角形。( )2.△ABC中∠A、∠B、∠C的对边分别是a、b、c,下列命题中的假命题是( )A.如果∠C-∠B=∠A,则△ABC是直角三角形。B.如果c2= b2 -a2,则△ABC是直角三角形,且∠C=90°。C.如果(c+a)(c-a)=b2,则△ABC是直角三角形。D.如果∠A:∠B:∠C=5:2:3,则△ABC是直角三角形。3.下列四条线段不能组成直角三角形的是( )A.a=8,b=15,c=17 B.a=9,b=12,c=15 C.a=√5 ,b=√3 ,c=√2 D.a:b:c=2:3:4
【教学目标】:
1、掌握直角三角形全等的判定定理,并能应用定理解决与直角三角形有关的问题。
2、进一步掌握推理证明的方法,拓发展演绎推理能力,培养思维能力。
【教学重难点】:
理解,掌握直角三角形全等的条件:HL.
【自学指导】:
一 、学生看P13---P14并思考一下问题:
“HL”中“H”代表什么?“L”代表什么?“HL”表示的是什么意思?
如何验证“HL”可以判定两个三角形全等?
到目前为止,我们学习了几种三角形全等的判别方法?各是什么?那么对于直角三角形全等的判别方法有几种?
运用“HL”证明直角三角形全等通常写成什么格式?
通常写成下面的格式:
在Rt△ABC与Rt△DEF中,
∵
∴Rt△ABC≌Rt△DEF(HL)
二、自学检测:
1.请判断满足下列条件的两个直角三角形是否全等,若不全等,在括号内打“×”,若全等,在括号内注明理由。
1.一个锐角和这个锐角的对边对应相等; ( )
2.一个锐角及和锐角相邻的一直角边对应相等;( )
3.一锐角与斜边对应相等; ( )
4.两直角边对应相等; ( )
5.两边分别相等; ( )
6.斜边和一条直角边对应相等的两个三角形. ( )
2.如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5) 若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
3.如图,AB⊥BD,CD∥AB,AB=CD,点E、F在BD上,且AE=CF.试说明AE∥CF.
三、师生共同探讨,总结:
@@@思考:证明线段相等,证明两个角相等我们现在用什么方法?由三角形全等到线段相等,角相等,还可由角相等到线平行。
四、例题讲解:
五、提高练习:
1.已知:如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=DC.证明:BE=DF
六、作业与学后反思:
1. 已知:如图,AB=CD, E、F在AC上,∠AFB=∠CED=90°,AE=CF.
(1)△ABF与△CDE全等吗?为什么?
(2)你发现AB与CD除相等外还有什么关系?如有就说明理由.
。
2. 如图,△ABC中,∠C=90°,AB=2AC,M是AB的中点,点N在BC上,MN⊥AB。
求证:AN平分∠BAC。
3. 如图,AB=CD,DF⊥AC于F,BE⊥AC于E,DF=BE,求证:AF=CE.
五.作业
课后反思
1.4角的平分线的性质(1)
学习目标:1、通过探究理解角平分线的性质并会运用2、掌握尺规作图作角平分线
学习重点:角平分线的性质及尺规作图
【学习过程】
一、预习导学:基本定理的学习:(阅读课文P22-25的内容)
角的平分线性质定理和判定定理:
二、讨论展示:
(1)知识回顾: 如图,已知AB=AD,BC=DC,求证:AC是∠DAB的平分线
(2)学习新知:
如图,已知∠BAC,用尺规作图的方法作出∠BAC的角平分线AD,
写出作法,并说明这种作法的依据。
2、OC是∠AOB的平分线,点P是射线OC上的任意一点,
操作测量:取点P的三个不同的位置,分 ( http: / / www.21cnjy.com )别过点P作PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:观察测量结果,猜想线段PD与PE的大小关系,写出结论
PD PE
第一次
第二次
第三次
3、你能用所学知识证明以上你发现的结论吗?
已知:AD平分∠BAC,P为AD上的一点,PM⊥AB,PN⊥AC
求证:
证明:
反过来,如图,若P为∠BAC内的一点,且点P到边AB、AC的距离相等,即PM=PN,你认为经过点P的射线AD平分∠BAC吗?为什么?
小结:通过以上探索和证明,我们得出了角平分线的性质是:
(1) ;
(2) 。
仔细比较分析,以上两条定理有什么关系:
一般情况下,我们要证明一个几何中的命题时,会按照类似的步骤进行,即:
(1) ;(2) ;(3) 。
三、新知应用:
(1)如图,已知AD是△ABC的角平分线,且D为BC的中点,DE⊥AB,DF⊥AC,
求证:BE=CF
2.1 多边形的内角和导学案
【学习目标】
1.知道多边形的内角和与外角和定理;
2.运用多边形内角和与外角和定理进行有关的计算.
【学习重难点】
重点:多边形的内角和与外角和定理; 难点:内角和定理的推导
【知识链接】
1.三角形的内角和是多少?
2.n边形从一个顶点出发的对角线有____条?它们将n边形分成____个三角形?
3.你知道长方形和正方形的内角和是多少?其它四边形的内角和是多少?
【合作探究】
知识点一:多边形的内角和定理
探究1:任意画一个四边形,量出它的4个内角,计算它们的和.再画几个四边形,量一量、算一算.
你能得出什么结论? 能否利用三角形内角和等于180°得出这个结论?
结论: .
探究2:从上面的问题,你能想出五边形和六边形的内角和各是多少吗?
观察图3,请填空:
(1)从五边形的一个顶点出发,可以引_____条对角线,它们将五边形分为_____个三角形,五边形的内角和等于180°×______.
(2)从六边形的一个顶点出发,可以引_____条对角线,它们将六边形分为_____个三角形,六边形的内角和等于180°×______.
探究3:一般地,怎样求n边形的内角和呢?请填空:
从n边形的一个顶点出发,可以引____条对角线,它们将n边形分为____个三角形,n边形的内角和等于180°×______.
结论:多边形的内角和与边数的关系是 .
练习:
1.十二边形的内角和是_________.
一个多边形的内角和等于900°,求它的边数.
知识点二:多边形的外角和
探究4:如图8,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
问题:如果将六边形换为n边形(n是大于等于3的整数),结果还相同吗?
因此可得结论: .
对应练习:
七边形的外角和是_________;十二边形的外角和是____________;三角形的外角和是_______.
一个多边形的每一个外角都等于36°则这个多边形是_______边形.
在每个内角都相等的多边形中,若一个外角是它相邻内角的1/2,则这个多边形是______边形.
【整理学案】通过本节课学习,你有什么收获?
【达标测试】
一个多边形的每一个外角都等于40° ( http: / / www.21cnjy.com ),则它的边数是__________;一个多边形的每一个内角都等于140°,则它的边数是___________.
如果四边形有一个角是直角,另外三个角的度数之比为2:3:4,那么这三个内角的度数分别为________.
3、若一个多边形的内角和为1080°,则它的边数是___________.
当一个多边形的边数增加1时,它的内角和增加_________度.
5、正十边形的一个外角为______.
6、_______边形的内角和与外角和相等.
7、已知一个多边形的内角和与外角和的差为1080°,则这个多边形是_____边形.
8、若一个多边形的内角和与外角和的比为7:2,求这个多边形的边数。
探 究:
把一块四边形的木料锯掉一个角后,所得的多边形的内角和为多少度?
多边形的内角和与外角和 习题精选(一)
1.n边形的内角和=________度,外角和=_______度。
2.从n边形(n>3)的一个顶点出发,可以画_______条对角线, ( http: / / www.21cnjy.com )这些对角线把n边形分成______三角形,分得三角形内角的总和与多边形的内角和_______。 ( http: / / www.21cnjy.com )
3.如果一个多边形的内角和与它的外角和相等,那么这个多边形是____边形。
4.如果一个多边形的内角和等于它的外角和5倍,那么这个多边形是____边形。
5.若n边形的每个内角都是150°,则n=____。
6.一个多边形的每个外角都是36°,这个多边形是______边形。
7.如果一个多边形的每个内角都相等,且内 ( http: / / www.21cnjy.com )角的度数是与它相邻的外角度数的2倍,那么这个边形的每个内角是_____度,其内角和等于______度。
8.若一个多边形的内角和是1800°,则这个多边形的边数是_______。
9.若一个多边形的边数增加1,则它的内角和 ( ) ( http: / / www.21cnjy.com )
A.不变 B.增加1 C.增加180° D.增加360°
10.当一个多边形的边数增加时,其外角和 ( )
A.增加 B.减少 C.不变 D.不能确定
11.某学生在计算四个多边形的内角和时,得到下列四个答案,其中错误的是( )
A.180° B.540° C.1900° D.1080°
12.分别画出下列各多边形的对角线,并观察图形完成下列问题:
(1)试写出用n边形的边数n表示对角线总条数S的式子:__________。
(2)从十五边形的一个顶点可以引出______条对角线,十五边形共有______条对角线:
(3)如果一个多边形对角线的条数与它的边数相等,求这个多边形的边数。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
13.n边形的内角和等于______度。任意多边形的外角和等于______度。
14.一个多边形的外角和是它的内角和的 ( http: / / www.21cnjy.com ),这个多边形是______边形。
15.如果十边形的每个内角都相等,那么它的每个内角都等于______度,每个外角都等于______度。
16.若多边形的内角和是1080°,则这个多边形是______边形。
17.如果一个多边形的内角和是720°,那么这个多边形的对角线的条数是( )
A.6 B.9 C.14 D.20
18.如果一个多边形的内角和是它的外角和的n倍,则这个多边形的边数是( )
A.n B.2n-2 C.2n D.2n+2
19.一个多边形截去一个角(不过顶点)后,形成的多边形的内角和是2520°,那么原多边形的边数是( )
A.13 B.14 C.15 D.13或15
20.若两个多边形的边数之比为1:2,两个多边形的内角和之和为1440°,求这两个多边形的边数。
21.判断:外角和等于内角和的多边形一定是四边形。( )
22.一个多边形的内角和是它的外角和的4倍,这个多边形是 ( )
A.四边形 B.六边形 C.八边形 D.十边形
23.一个多边形中,除一个内角外,其余各内角和是120°,则这个角的度数是( )
A.60° B.80° C.100° D.120°
24.如果一个多边形的内角和等于1800°,则这个多边形是______边形;如果一个n边形每一个内角都是135°,则=n______;
如果一个n边形每一个外角都是36°,则=n______。
25.某学校艺术馆的地板由三种正多边形的小木板铺成,设这三种多边形的边数分别为x、y、z,求 ( http: / / www.21cnjy.com )的值。
2.2.1平行四边形的性质学案1
一.温故知新:
1.有两组对边__________________的四边形叫平形四边形,平行四边形用“______”表示,平行四边形ABCD记作__________。
2.如图□ABCD中,对边有______组,分别是___________________,对角有_____组,分别是_________________,对角线有______条,它们是___________________。
二.学习新知:
1.自学课本P83~P84,填空:平行四边形的性质
(1)边:_________________________________________________________
(2)角:_________________________________________________________
例:□ABCD中,如果AB∥CD,那么AB=______,BC=______,∠A=______,∠B=______.
2.看例1,完成课本P84的练习.
三.释疑提高:
1.□ABCD中,两邻角之比为1∶2,则它的四个内角的度数分别是____________.
2.□ABCD的周长是28cm,△ABC的周长是22cm,则AC的长是__________.
3.如图,在□ABCD中,M、N是对角线BD上的两点,BN=DM,请判断AM与CN有怎样的数量关系,并说明理由.它们的位置关系如何呢?
( http: / / www.21cnjy.com )
4.如图,在□ABCD中,AE ( http: / / www.21cnjy.com )⊥BC于E,AF⊥CD于F,若∠EAF=60°,BE=2cm,DF=3cm,求□ABCD的周长和面积. 若问题改为CF=2cm,CE=3cm,求□ABCD的周长和面积.
( http: / / www.21cnjy.com )
5.□ABCD中,E在边AD上,以BE ( http: / / www.21cnjy.com )为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△FDE的周长为8,△FCB的周长为22,求CF的长.
( http: / / www.21cnjy.com )
四.小结归纳:
五.巩固检测
1.课本P—1、2 2.课堂作业平行四边形性质1
2.2.1平行四边形的性质学案2
一.温故知新:
1.平行四边形的定义是:_______________________________________________.
2.所学平行四边形的性质有:平行四边形的对边______________,平行四边形的对角______________.
3.如图,在□ABCD中,BC=2AB,M是AD的中点,则∠BMC=___________.
二.学习新知:
1.自学课本P85~86内容,填空:
平行四边形的又一个性质是:______________________________,当图形中没有平行四边形的对角线时,往往需作出对角线.
由此得到平行四边形的性质有:
(1)边:_____________ (2)角:_____________ (3)对角线:_____________
2.看例2,完成课本P86的练习.
三.释疑提高:
1.在□ABCD中,AC、B ( http: / / www.21cnjy.com )D交于点O,已知AB=8cm,BC=6cm,△AOB的周长是18cm,那么△AOD的周长是_____________.
2. □ABCD的对角线交于点O,S△AOB=2cm2,则S□ABCD=__________.
3. □ABCD的周长为60cm,对角 ( http: / / www.21cnjy.com )线交于点O,△BOC的周长比△AOB的周长小8cm,则AB=______cm,BC=_______cm.
4. □ABCD中,对角线AC和BD交于点O,若AC=8,AB=6,BD=m,那么m的取值范围是____________.
5. □ABCD中,E、F在AC上,四边形DEBF是平行四边形.求证:AE=CF.
( http: / / www.21cnjy.com )
6.如图,田村有一口四边形的池塘,在它 ( http: / / www.21cnjy.com )的四角A、B、C、D处均有一棵大桃树.田村准备开挖养鱼,想使池塘的面积扩大一倍,并要求扩建后的池塘成平行四边形形状,请问田村能否实现这一设想?若能,画出图形,说明理由.
( http: / / www.21cnjy.com )
四.小结归纳:
五.巩固检测
1.作业精编 2.课堂作业平行四边形性质2
2.2.2平行四边形的判定学案1
一.温故知新
1.如图在平行四边形ABCD中,DB=DC,∠A=65°,CE⊥BD于E,则∠BCE= .
2.如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F,已知AE=4,AF=6,□ABCD的周长为40,试求□ABCD的面积。
二.学习新知
1.自学课本P86-P87,掌握平行四边形的判定定理,注意定理条件和结论,并会证明。
2.自学例子,并证明。 独立完成P87的练习。
三.释疑提高
1.以不共线的三点A、B、C为顶点的平行四边形共有 个。
2.一个四边形的边长依次为a、b、c、d,且a2+b2+c2+d2=2ac+2bd,
这个四边形是 。
3.如图,在△ABC的边AB上截取AE=BF,过E作ED∥BC交AC于D,
过F作FG∥BC交AC于G,求证:ED+FG=BC。
( http: / / www.21cnjy.com )
4.如图,线段AB、CD相交于点O,AC∥DB,AO=BO,E、F分别为OC、OD的中点,连结AF、BE,求证AF∥BE。
5.如图,已知O是平行四边形ABCD对角 ( http: / / www.21cnjy.com )线AC的中点,过点O作直线EF分别交AB、CD于E、F两点,(1)求证:四边形AECF是平行四边形;(2)填空,不填辅助线的原因中,全等三角形共有 对。
6.如图,在□ABCD中,点E是AD的中点, ( http: / / www.21cnjy.com )BE的延长线与CD的延长线相交于点F,(1)求证:△ABE≌△DFE;(2)试连结BD、AF,判断四边形ABDF的形状,并证明你的结论。
四.小结归纳
五.巩固检测1.习题-1、4、5、8、9、10、11
2.2.2平行四边形的判定学案2
一.温故知新
1.如图在□ABCD中,EF∥AD,MN∥AB,EF、MN相交于点P,图中共有 个
平行四边形。
2.如果平行四边形的两条对角线长分别为8和12,那么它的边长不能取( )
A. 10 B. 8 C. 7 D. 6
3.如图,在□ABCD中,AC、BD ( http: / / www.21cnjy.com )交于点O,EF过点O分别交AB、CD于E、F,AO、CO的中点分别为G、H,求证:四边形GEHF是平行四边形。
二.学习新知
1.自学课本P88平行四边形的判定定理,注意定理条件和结论,并会证明。
2.自学例子,掌握三角形中位线概念和中位线定理,并会证明。
3.掌握平行线间的距离。 4.完成P90面练习1.2.3。
三.释疑提高
1.如图,△ABC是等边三角形,P是其 ( http: / / www.21cnjy.com )内任意一点,PD∥AB,PE∥BC,DE∥AC,若△ABC周长为8,则PD+PE+PF= 。
2.四边形ABCD是平行四边形,BE平分∠ABC交AD于E, DF平分∠ADC交BC于点F,求证:四边形BFDE是平行四边形。
3.已知□ABCD中,E、F分别是AD、BC的中点,AF与EB交于G,CE与DF交于H,求证:四边形EGFH为平行四边形。
4.如图,在四边形ABCD中,AB=6,BC=8,∠A=120°,∠B=60°,∠BCD=150°,求AD的长。
( http: / / www.21cnjy.com )
5.已知BE、CF分别为△ABC中∠B、∠C的平分线,AM⊥BE于M,AN⊥CF于N,求证MN∥BC。
( http: / / www.21cnjy.com )
6.如图,在□ABCD中,EF∥AB交BC于E,交AD于F,连结AE、BF交于点M,连结CF、DE交于点N,求证:(1)MN∥AD;(2)MN= HYPERLINK "http://www.21cnjy.com" AD。
四.小结归纳
八年级几何四边形练习题
1、已知四边形ABCD为正方形,M为AB中点,N为AD上一点,且CN=AB+AN.
求证:CM平分∠BCN.
已知如图, 四边形ABCD是平行四边形,E为AC上一点,F为AB上一点,
且AE=2EC,BF=2AF,若S
△BEF=2,求S□ABCD.
3、已知,四边形ABCD是平行四边形,EF垂直平分BD,垂足为O,
交BA、DC的延长线于E、F.求证:四边形EBFD为菱形.
4、如图,D为AB中点,DE∥BC交AC于E点.
5、如图梯形ABCD中,AD∥BC,E为AB中点,F为DC中点,EF、BD交于G点.
求证:G为BD中点.
6、如图△ABC中,∠B=90°,∠BAC=78°,FC∥AB,BC交AF于G点,
且FG=2AC.求∠BAG.
7、已知如图, 梯形ABCD中,E为DC中点,若梯形ABCD=10.
(1)求S△EBA.(2)若AB=AD+BC,求证:AE⊥BE.
8、已知如图, 四边形ABCD是矩形,AE平分∠BAD,EF交BD于F点,
交AC于G点,若GA=GE,求证:EF⊥BD.
9、已知如图D为△ABC边AB的中点,E在BC上,且BE= HYPERLINK "http://www.21cnjy.com" BC, 且CD、AE交于P点, 若S△APC=8,求S△ABC.
10、已知,如图,正方形ABCD中,AC、BD交于O点,EA平分∠BAC交BD于F点.求证:FO= HYPERLINK "http://www.21cnjy.com" EC.
11、已知如图, 四边形ABCD是平行四边形,
直线 HYPERLINK "http://www.21cnjy.com" 上有点M、N、P、Q,且BM⊥ HYPERLINK "http://www.21cnjy.com" ,
AN⊥ HYPERLINK "http://www.21cnjy.com" ,CP⊥ HYPERLINK "http://www.21cnjy.com" ,DQ⊥ HYPERLINK "http://www.21cnjy.com" .求证:DM+BQ=AN+CP.
正方形ABCD中,E为BC上一点,F为DC上一点,AE⊥BF,
连AC,O为AC中点,连OE、OF,求证:(1)BE=CF;(2)OE⊥OF;
(3)若S正方形=1,求S四边形OECF.
13、如图,等腰梯形ABCD中,AD∥BC,AB=CD.
(1)将△ABC沿BC向下翻折到△CBE的位置,试判断四边形DBEC的形状,并证明你的结论.
(2)翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点G、F,
若∠CBD=45°,AD=4,BC=8求BF的长。
14,如图,直线y= HYPERLINK "http://www.21cnjy.com" x+5与x轴、y轴交于A、B两点,过点C(-7,2)作CD⊥x轴于D,连CA.(1)求证:AC=AB,且AC⊥AB;(2)在y轴上取点E(0,3),连DE
交AB于点P,求∠APD的度数.
16、已知等腰梯形ABCD中,AD∥BC,AB=DC,点P是BC边上一点,PE⊥AB,PF⊥CD,BG⊥CD.求证:PE+PF=BG.
平行四边形测试题
一、选择题(每题3分,共30分)
1.在□ABCD中,∠A∶∠B∶∠C∶∠D的值可以是( )
A.1∶2∶3∶4 B.1∶2∶2∶1
C.1∶1∶2∶2 D.2∶1∶2∶1
2.平行四边行的两条对角线把它分成全等三角形的对数是( )
A.2 B.4 C.6 D.8
3.在□ABCD中,∠A、∠B的度数之比为5∶4,则∠C等于( )
A.60° B.80° C.100° D.120°
4、一个四边形的三个内角度数依次如下,那么其中是平行四边形的是( )
A、88°,108°,88° B、88°,104°,108°
C、88°、92°、92° D、88°,92°,88°
5、下列哪组条件能判别四边形ABCD是平行四边形?( )
A、AB∥CD,AD=BC B、AB=CD,AD=BC
C、∠A=∠B,∠C=∠D D、AB=AD,CB=CD
6、平行四边形的一边长为10,那么它的两条对角线的长度可以是( )
A、8和12 B、4和16 C、20和30 D、8和6
7. HYPERLINK "http://www.21cnjy.com" ABCD的周长为40 cm,△ABC的周长为25 cm,则对角线AC长为( )
A.5 cm B.15 cm C.6 cm D.16 cm
8.□ABCD的周长为36 cm,AB=5/7BC,则较长边的长为( )
A.15 cm B.7.5 cm C.21 cm D.10.5 cm
9.如图,□ABCD中,EF过对角线的交点O,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )A.8.3 B.9.6 C.12.6 D.13.6 HYPERLINK "http://www.21cnjy.com" (图9) (图10)
10.如图,在平面直角坐标系中, ( http: / / www.21cnjy.com )□ABCD的顶点A、B、D的坐标分别是(0,0),(5,0)(2,3),则顶点C的坐标是( )A.(3,7) B.(5,3) C.(7,3) D.(8,2)
二、填空题(本大题8个小题,每小题3分,共24分)
11、在平行四边形中,若一个角为其邻角的2倍,则这个平行四边形中两邻角的度数分别是 。
12、设点O是□ABCD对角线的交点,如果□ABCD的面积为20cm2,则△AOB的面积为 。
13、若平行四边形的一边长为8cm,一条对角线长为6cm,则另一条对角线长χ(cm)的取值范围为 。
14、□ABCD的周长为36cm,AB=8cm,则BC= cm。
15、已知平行四边形的面积为144,相邻两边上的高分别为8和9,则它的周长为 。
16、已知a、b、c、d为四边形的 ( http: / / www.21cnjy.com )四边长,a、c为对边,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形一定是 。
17.能判定四边形ABCD为平行四边形的题设是: 。(只填字母序号)
(A)AB∥CD,AD=BC; (B)∠A=∠B,∠C=∠D; (C)AB=CD,AD=BC;
(D)AB=AD,CB=CD (E)AB HYPERLINK "http://www.21cnjy.com" CD (F)AB∥CD,AD∥BC (G)OA=OC,OB=OD
18、如图,P为□ABCD的对角线B ( http: / / www.21cnjy.com )D上一点,过P作GH∥CD,EF∥BC,写出图中你认为面积相等的平行四边形有 。
(说明:可写成S □ABCD =S□ … … 的形式)
三、解答题(共46分)解答时请写出必要的演算过程或推理步骤。
19、(10分)已知:在□ABCD中,∠A的 20.(11分)如图,在□ABCD中,
角平分线交CD于E,若 HYPERLINK "http://www.21cnjy.com" , AB=8cm,BC=10cm,∠C=120°,
AB的长为8,求BC的长。 (1)求BC边上的高AH的长;
(2)求□ABCD的面积.
21、(12分)如图,AC是□ABCD的 22.(13分)如图,在△ABC中,AB=AC,
对角线,MN∥AC,分别交AD、CD 点D在BC上,DE∥AC,DF∥AB,
于点P、Q,试说明MP=QN。 (1)求证:FD=FC
(2)若AC=6cm,试求四边形AEDF的 周长。
中心对称和中心对称图形导学案P51
教学目标:
1、知道中心对称和中心对称图形的意义。
2、知道中心对称的两个图形的特征。
3、能运用中心对称的性质做出一个图形关于某点对称的中心对称图形。
教学重难点:
重点:1、中心对称图形和中心对称的概念及特征。
2、作已知图形关于某点为对称中心的中心对称图形。
难点:中心对称图形与中心对称之间的区别与联系。
任务一:探索中心对称的定义:
问题1:这些图形有什么共同的特征?
问题2:你能将上图中的图形绕某点旋转180°,使旋转后的图形与原图形完全重合吗?请选取其中的一个图形加以解释。
归纳总结:
在平面内,一个图形绕某个点旋转 ( http: / / www.21cnjy.com ) ,如果旋转前后的图形互相 ,那么这个图形叫做 ,这个点叫做它的 。
左图是一幅中心对称图形,O是 ( http: / / www.21cnjy.com )对称中心,请你找出点A绕点O的旋转180O后的对应点B;AO=BO吗?其他的对应点到对称中心的距离呢?由此你会得到怎样的结论?
任务二:学以致用:
1.下面哪个图形是中心对称图形?
2、下列图形是中心对称图形的是( )
3、在一次游戏当中,小明将下面左图的四张扑克牌中的一张旋转180O后,得到右图,小亮看完很快知道小明旋转了哪一张扑克,你知道为什么吗?
4、在26个英文大写正体字母中,哪些字母是中心对称图形
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
任务三:能力提升:
1、请以给定的图形○○△△ ( http: / / www.21cnjy.com )=(两个圆,两个三角形,两条平行线)为构件,尽可能多地构思有意义的一些中心图形,并写上一两句贴切,诙谐的解说词.如下图就是符合要求的图形,你能构思其它图形吗 比一比,看谁想得多,看谁想得妙!
2、举出常见的中心对称图形。
二、填空题(每题 3 分,共 12 分)
3.写出几个是中心对称的汉字:
4 .如图 15-3-3 所示, △OA B 绕点O旋转 180°得到 △OCD ,
连结 AD 、 BC ,得到四边形ABCD ,则 AB________CD (填位置
关系);与 △AOD成中心对称的是__________由此可得到 AD______ BC(填位置关系).
5 .从数学对称的角度看,下面几组大写英文字母: ① ANEG ; ② GBXM ; ③ XIHO ; ④ ZDWH .不同于另外三组的 ( http: / / www.1230.org / )-组是_________,这-组英文字母的特点是__________.
6.正方形既是_________图形,又是 ( http: / / www.21cnjy.com )_____________图形,它有_____________条对称轴,对称中心是_____________________
三、计算题( 10 分)
7 .如图所示,是跷跷板图,AO和BO等长, ( http: / / www.21cnjy.com )横板AB通过点O,且可以绕O点上下转动,如果∠OCA=90°,∠CAO= 25° ,问小孩玩跷跷板时上下最多可以转动多少度?
图
四、解答题(每题 10 分,共 20 分)
8.如图 15-3-5 所示,已知 MN⊥PQ , 垂足为O ,点 A 、A1 是以 MN 为轴的对称点,而点 A 、 A2 是以PQ 为轴的对称点,则点 A1、A2 关于点O成中心对称,你能说明其中的道理吗?
课题: 三角形的中位线
一 学习目标
1了解三角形的中位线的定义,注意与三角形的中线的区别
2 掌握三角形的中位线定理,并能灵活的运用
重点:识记三角形的中位线定义、定理
难点:三角形中位线定理的灵活应用
二 自主预习
1 三角形的中位线
连接三角形的两边 的线段,叫做三角形的中位线。
2 三角形的中位线定理
三角形的中位线平行于 ,并且等于 。
三 课内探究
探究一 三角形的中位线及其性质
任意画△ABC,设AB,AC边的中点分别为D,E,连接DE.
连接三角形 ,叫做 ,
画一画,三角形有几条中位线。
。
在图1中分别度量∠ADE与∠B的大小,你发现DE与BC有怎样的位置关系?
分别量出线段DE与BC的长,你发现DE与BC之间有怎样的数量关系?
?
对于△ABC其他的两条中位线,重复(2)中实验,你得到了什么结论?
归纳(2)(3)的结论,你认为三角形的中位线具有什么性质?
结论:
(5)如图,把△ABC沿中位线DE剪开,得到△ADE和四边形BCDE,将△ADE绕点E旋转1800,使点A与点C重合,你拼出一个什么图形?
上面(5)中得拼图过程对于证明你所发现的命题有什么启示?
(7)已知:如图,在△ABC中,点D,E分别是AB与AC边的中点。
求证:DE∥BC,DE= HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 BC
于是就证明了(2)中发现的命题,我们把它叫做三角形的中位线定理
三角形的中位线定理:
三角形中位线的应用
1 .如图所示,□ ABCD的对角线AC,BD相交于点O,AE=EB,求证:OE∥BC.
2.如图所示,在△ABC中,点D在BC上且CD=CA,CF平分∠ACB,AE=EB,求证:EF= HYPERLINK "http://www.21cnjy.com" BD.
3.如图所示,已知在□ABCD中,E,F分别是AD,BC的中点,求证:MN∥BC.
4.已知:如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
5.已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.
求证:四边形DEFG是平行四边形.
6.已知:如图,E为□ABCD中DC边的延长线上的一点,且CE=DC,连结AE
分别交BC、BD于点F、G,连结AC交BD于O,连结OF.求证:AB=2OF.
2.5.1矩形的性质学案 P58
一、温故知新:回顾平行四边形有哪些性质?然后填空。
1、平行四边形的__________相等。表示方法:若四边形ABCD是平行四边形,则___________;
2、平行四边形的__________相等。表示方法:若四边形ABCD是平行四边形,则___________;
3、平行四边形的对角线________.表示方法: HYPERLINK "http://www.21cnjy.com" 在□ ABCD中,AC与BD相交于O,则______________
4、平行四边形的对称性:平行四边形是___对称图形,而不是______对称图形,对角线的交点是平行四边形的_________.
二、学习新知:自学P94-95页。
自学引导:①平行四边形活动框架在变化过程中,哪些量发生了变化?哪些量没有变化?从中得到哪些结论?你能试着说明结论是否成立?
②矩形的一条对角线把矩形分成两个什么三角形?矩形的两条对角线把矩形分成四个什么样的三角形?
1.矩形的定义:有一个角是直角的平行四边形,叫做矩形。由此可见,矩形是特殊的 ,它具有平行四边形的所有性质。
2.结合上面两个图形说说矩形有哪些平行四边形不具有的特殊性质?
.
3.证明:矩形的四个角都是直角
已知:如图, 图形:画在下面
求证:___________________
证明:
证明:矩形对角线相等
已知:如图, 图形:画在下面
求证:
证明:
三、探索活动
问题一 如图,矩形ABCD,对角线相交于O,观察对角线所分成的三角形,你有什么发现?
( http: / / www.21cnjy.com )
问题二 将目光锁定在Rt△ABC中,你能发现它有什么特殊的性质吗?
证明:“直角三角形斜边上的中线等于斜边的一半.”
已知: 图形:画在下面
求证:
证明:
问题三 上面结论的逆命题是: 。
是否正确?请给予证明。
四、例题学习
例:已知:如图,矩形ABCD的两条对角线相交于点O,且AC=2AB。求证:△AOB是等边三角形。(注意表达格式完整性与逻辑性)
( http: / / www.21cnjy.com )
拓展与延伸:本题若将“AC=2AB”改为“∠BOC=120°”,你能获得有关这个矩形的哪些结论?
五、练习
1、P 1
2、已知:如图,E为矩形ABCD内一点,且EB=EC。求证:EA=ED.
( http: / / www.21cnjy.com )
六、本节课你的收获是什么?
七、提高训练:1.如图,矩形纸片ABCD,且AB=6cm,宽BC=8cm,将纸片沿EF折叠,使点B与点D重合,求折痕EF的长。
( http: / / www.21cnjy.com )
2.已知矩形ABCD中,对角线交于点O,A ( http: / / www.21cnjy.com )B=6cm,BC=8cm,P是AD上一动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值是多少?这个值会随点P的移动(不与A、D重合)而改变吗?请说明理由.
( http: / / www.21cnjy.com )
3.已知:如图,矩形ABCD的两条对角线AC、BD相交于点O,∠BOC=120°,AB=4cm。求矩形对角线的长。
( http: / / www.21cnjy.com )
4.如图,在矩形ABCD中,BE平分∠ABC,交CD于点E,点F在边BC上,
如果FE⊥AE,求证FE=AE。②如果FE=AE 你能证明FE⊥AE吗?
2.5.2矩形的判定学案
一、温故知新:1.矩形是轴对称图形,它有______条对称轴.
2.在矩形ABCD中,对角线AC,BD相交于点O,若对角线AC=10cm,边BC=8cm,则△ABO的周长为________.
3.想一想:矩形有哪些性质?在这些性质中那些是平行四边形所没有的?列表进行比较.
平行四边形 矩形
边
角
对角线
二、学习新知:自学教材95—96页
1、矩形是特殊的平行四边形,怎样判定一 ( http: / / www.21cnjy.com )个平行四边形是矩形呢 请说出最基本的方法:
矩形具有平行四边形不具有的性质是:
思考:小华想要做一个矩形像框送给妈 ( http: / / www.21cnjy.com )妈做生日礼物,于是找来两根长度相等的短木条和两根长度相等的长木条制作,你有什么办法可以检测他做的是矩形像框吗?看看谁的方法可行?(得到矩形的一个判定)
2.做一做:按照画“边 ―直角、 ( http: / / www.21cnjy.com )边-直角、边-直角、边”这样四步画出一个四边形.判断它是一个矩形吗 说明理由. (探索得到矩形的另一个判定)
总结:矩形的判定方法. 矩形判定方法1:______________________________
矩形判定方法2:_______________________________
(指出:判定一个四边形是矩形,知道三个角是直角,条件就够了.因为由四边形内角和可知,这时第四个角一定是直角.)
3.议一议:下列各句判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形;( ) (2)有四个角是直角的四边形是矩形;( )
(3)四个角都相等的四边形是矩形;( ) (4)对角线相等的四边形是矩形;( )
(5)对角线相等且互相垂直的四边形是矩形;( )(6)对角线互相平分且相等的四边形是矩形;( )
(7)对角线相等,且有一个角是直角的四边形是矩形; ( )
(8)一组邻边垂直,一组对边平行且相等的四边形是矩形;( )
(9)两组对边分别平行,且对角线相等的四边形是矩形. ( )
三、例题学习。例1.:已知□ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积.
( http: / / www.21cnjy.com )
已知:如图,□ABCD的四个内角的平分线分别相交于点E、F、G、H.求证:四边形EFGH是矩形.
( http: / / www.21cnjy.com )
练习二:(选择)下列说法正确的是( ).
(A)有一组对角是直角的四边形一定是矩形(B)有一组邻角是直角的四边形一定是矩形
(C)对角线互相平分的四边形是矩形 (D)对角互补的平行四边形是矩形
2.满足下列条件( )的四边形是矩形。
A.有三个角相等 B.有一个角是直角 C.对角线相等且互相垂直 D.对角线相等且互相平分
3 .已知:如图 ,在△ABC中,∠C=90°, CD为中线,延长CD到点E,使得 DE=CD.连结AE,BE,则四边形ACBE为矩形.
( http: / / www.21cnjy.com )
4.已知:如图,在平行四边形ABCD中,E为CD中点,三角形ABE是等边三角形,求证:四边形ABCD是矩形。
( http: / / www.21cnjy.com )
四:处理教材96页练习2,102页习题2、3。
五:你学到了什么?相互说一说。
六、巩固训练:
1、在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( ).
A.测量对角线是否相互平分 B.测量两组对边是否分别相等
C.测量一组对角是否都为直角 D.测量其中三角形是否都为直角
2、能判断四边形是矩形的条件是( )
A、两条对角线互相平分 B、两条对角线相等
C、两条对角线互相平分且相等 D、两条对角线互相垂直。
3、如图,EB=EC,EA=ED,AD=BC, ∠AEB=∠DEC,证明:四边形ABCD是矩形.
( http: / / www.21cnjy.com )
4、已知四边形ABCD中AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点,求证:四边形EFGH是矩形。
5、如图,M、N分别是平行四边形ABCD对边AD、BC的中点,且AD=2AB,
求证,四边形PMQN是矩形。
( http: / / www.21cnjy.com )
2.6.1 菱形的性质学案
一、研读教材,解读目标:
1、 叫做菱形。菱形是 的平行四边形。
2、探究菱形的性质,并用模式表述菱形的特殊性质:
3、解析教材97页探究与98页例题2与练习题1、2,102页习题5、11、12
二、知识梳理
有一组邻边相等的平行四边形叫菱形.与一般平行四边形相比,菱形具有哪些性质?
定理: (菱形的边) (菱形的角)
定理: ______________ (菱形的对角线)
三、定理证明:(小组合作,先交流命题证明方法和步骤,然后自己完成证明再与组长交流)
( http: / / www.21cnjy.com )
四、典型例题
例3. 如图3个全等的菱形构成的活 ( http: / / www.21cnjy.com )动衣帽架,顶点A、E、F、C、G、H是上、下两排挂钩,根据需要可以改变挂钩之间的距离(比如AC两点可以自由上下活动),若菱形的边长为13厘米,要使两排挂钩之间的距离为24厘米,并在点B、M处固定,则B、M之间的距离是多少?
五、合作交流
1.证明:菱形的面积是它两条对角线长的乘积的一半.
2.已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是菱形ABCD各边的中点,求证:OE=OF=OG=OH.
( http: / / www.21cnjy.com )
六、小结
菱形的边和对角线有不同于一般的平行四 ( http: / / www.21cnjy.com )边形的性质,有关菱形的几何计算问题可以化为_______三角形(_____三角形、等腰三角形),利用特殊三角形的性质来计算。
七、课堂练习
1.己知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为 .
( http: / / www.21cnjy.com )
2.已知四边形ABCD是菱形,O是两条对角线的交点,AC=8cm,DB=6cm,这个菱形的边长是________cm.
3.已知菱形的边长是5cm,一条对角线长为8cm,则另一条对角线长为______cm.
4.四边形ABCD是菱形,∠ABC=1 ( http: / / www.21cnjy.com )20°,AB=12cm,则∠ABD的度数为____ , ∠DAB的度数为______;对角线BD=_______,AC=_______;菱形ABCD的面积为_______.
八、目标达成训练
1.下列图形中,即是中心对称图形又是轴对称图形的是 ( )
A.等边三角形 B.菱形 C.等腰梯形 D.平行四边形
2.(09河北)如图,在菱形ABCD中,AB = 5,∠BCD = 120°,则对角线AC等于( )
A.20 B.15 C.10 D.5
3.(09南宁)如图2, ( http: / / www.21cnjy.com )将一个长为10cm,宽为8cm的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )
A.10cm2 B.20cm2 C.40cm2 D.80cm2
第3题图 第5题图 第6题图 第7题图
4.菱形的两条对角线长分别为6和8,则它的面积为________,周长为_________。
5.(09宁波)如图,菱形ABCD ( http: / / www.21cnjy.com )中,对角线AC、BD相交于点O,M、N分别是边AB、AD的中点,连接OM、ON、MN,则下列叙述正确的是( )
A.△AOM和△AON都是等边三角形 B.四边形MBON和四边形MODN都是菱形
C.四边形AMON与四边形ABCD是位似图形 D.四边形MBCO和四边形NDCO都是等腰梯形
6.(选做,09杭州)如图,在菱形ABCD中,∠A=110°,E,F
分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )
A.35° B.45° C.50° D.55°
7.(选做,07咸宁)如 ( http: / / www.21cnjy.com )图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点E,交AB于点F,F为垂足,连接DE,则∠CDE=_________
8.求证:菱形的对角线的交点到各边的距离相等。
2.6.2菱形的判定学案
一:复习:菱形有哪些特殊性质?
边:__________________________;______________________________
角:__________________________;______________________________
对角线:_____________________________;___________________________________
二、学习新知
目标一:会用菱形的定义判定一个四边形是否是菱形,并会用该种方法进行有关的证明.
(菱形的判定方法一)菱形的定义:
有 的 叫做菱形.
2.用符号语言可以表示为:
∵四边形ABCD是 四边形 ∵ ___ =____, ∴□ ABCD是菱形
3.如图在△ABC中,AD平分∠BAC交BC于D点,过D作DE∥AC交AB于E点, 过D作DF∥AB交AC于F点.
求证:(1)四边形AEDF是平行四边形 (2)∠2﹦∠3 (3)四边形AEDF是菱形
( http: / / www.21cnjy.com )
目标二:探究并掌握菱形的判定方法二
1.( 画图)自学99页最后三行的画图过程,
用圆规画出菱形ABCD,图画在右边(保留作图痕迹)
2.你发现四边形ABCD四边的关系是:
3.(猜想)四边相等的四边形ABCD是一个_____形.
4.(证明)利用上图证明:“四边相等的四边形是菱形”
已知:如上图,在四边形_______中,____=____=____=____
求证:四边形ABCD是_____.
证明:
5.(总结)由上写出菱形的判定方法二:_______ .
利用上图用符号语言表示为:在四边形ABCD中,
∵ ____=____=____=____ ∴四边形ABCD是 形
目标三:探究并掌握菱形的判定方法三
阅读99页“探究”,利用自制的学具探究菱形的判定方法并完成下面各题
1.由“在一长一短的木条中点处固定一个小钉”可知: = , =
∴四边形ABCD是 四边形
2.转动十字,当∠_____= °时即___ ⊥ ___时,四边形变成了菱形.
3. (猜想)对角线互相____ 的平行四边形是菱形.
4.请利用下图证明你的猜想:
已知:如图,在□ABCD中,AC和BD是对角线,并且AC⊥BD于点O,求证:□ABCD是菱形.
( http: / / www.21cnjy.com )
5.总结写出菱形判定方法三:
利用上图用符号语言可以表示为:∵四边形ABCD是平行四边形,∵AC___BD,∴□ABCD是菱形
目标四:利用菱形判定方法进行计算和证明
1.自学99页例三完成下题“在□ABCD中,对角线AC和BD相交于点O,并且AB=9,OB=6,OA=3 HYPERLINK "http://www.21cnjy.com" .求证:(1)AC⊥BD (2)□ABCD是菱形吗?说说你的理由. (3)求四边形ABCD的面积.
( http: / / www.21cnjy.com )
2.判断题,对的画“√”错的画“×”
(1).对角线互相垂直的四边形是菱形( )
(2).一条对角线垂直另一条对角线的四边形是菱形( )
(3)..对角线互相垂直且平分的四边形是菱形( )
(4).对角线相等的四边形是菱形( )
三、小结:菱形的常用判定方法
四:拓展延伸
1.如图,两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是菱形吗?
求证:(1)四边形ABCD是平行四边形
(2) 过A作AE⊥BC于E点, 过A作AF⊥CD于F.用等积法说明BC=CD.
(3) 求证:四边形ABCD是菱形.
( http: / / www.21cnjy.com )
2.已知:如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形。
( http: / / www.21cnjy.com )
3. 如图,AC⊥BC,AE平分∠CAB,CD⊥AB,EF⊥AB,连接FG,求证:CEFG为菱形.
( http: / / www.21cnjy.com )
2.7正方形学案1
一.温故知新 填表:
性质 判定方法
矩形 边:角:对角线:对称性: 1.2.3.
菱形 边:角对角线:对称性: 1.2.3.
二.学习新知
自学教材100-101页,落实:
性质 判定方法
正方形 边:角对角线:对称性:
自学例4,并在学案上做一遍:
完成课本P101页练习1、2、3题
三.释疑提高
1.正方形的四条边____ __,四个角___ ____,两条对角线____ ____.
2.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD B. AD∥BC,∠A=∠C
C. AO=BO=CO=DO,AC⊥BD D. AO=CO,BO=DO,AB=BC
3.如图,正方形ABCD中,对角线 ( http: / / www.21cnjy.com )交于O,E是OB上一点,DG⊥AE于G,DG交OA于F.①求证:OE=OF. ②当E为OB延长线上一点时,画出对应的图形,观察①中结论是否仍然成立,并给予证明.
( http: / / www.21cnjy.com )
4.如图,正方形ABCD中,E、 ( http: / / www.21cnjy.com )F为BC、CD上两点,且∠EAF=45°,①求证:EF=BE+DF. ②以上命题的逆命题是否成立?③若AB=12,求△CEF周长.④若AB=12,EF=10,求△AEF面积.
( http: / / www.21cnjy.com )
四、小结归纳
五、巩固检测1.课本102页习题7、13、15; 2.作业精编19.2.3 正方形
2.7 正方形学案2
一、温故知新
1.有一组邻边____ __,且有一个角____ __的平行四边形是正方形。
2.正方形的四边____ __,四角____ __,对角线____ __且____ __;正方形既是矩形,又是____ _;既是轴对称图形,又是____ ______ __。
3.如图正方形ABCD的边长为8,DM=2,N为AC上一点,则DN+MN的最小值为 .
4.如图,正方形ABCD边长为2,两对角线交点为O,OEFG也为正方形,则图中阴影部分面积为 .
5.如图,若四边形ABCD是正方形,△CDE是等边三角形,则∠EAB的度数为 .
6. 如图,已知正方形AB ( http: / / www.21cnjy.com )CD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF的面积为200,则BE的值是 .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
二、学习新知
作业精编73页例1、例2(独立写出过程)
三、释疑提高
1.如图,正方形ABCD中,E为BC上一点,AF平分∠DAE,求证:BE+DF=AE.
( http: / / www.21cnjy.com )
2. 如图,正方形ABCD中,E为BC上一点,DF=CF,DC+CE =AE,求证:AF平分∠DAE.
( http: / / www.21cnjy.com )
3.如图,BF平行于正方形ADCD的对角线AC,点E在BF上,且AE=AC,CF∥AE,求∠BCF.
( http: / / www.21cnjy.com )
四、小结归纳
五、巩固检测:课堂作业P74和学法大视野
3.1 平面直角坐标系
◆回顾探索
1.平面直角坐标系:在平面上画 ( http: / / www.21cnjy.com )出两条原点重合,互相垂直且具有相同的_____的数轴,就叫建立平面直角坐标系,其中水平的一条数轴叫做______轴或______轴,取向_______为正方向,垂直的数轴叫_______轴或_______轴,取向_______为正方向.
2.对称点、特殊点的坐标的特征:(1)关于x轴对称的点的坐标,______相等,_____相反;
(2)关于y轴对称的点的坐标,________相等,_________相反.
(3)关于原点对称的点的坐标特征是____________.
(4)x轴上的点的坐标特征是:_________,y轴上的点的坐标特征是________.
◆课堂测控
测试点1 平面直角坐标系
1.如图,是象棋盘的一部分,若位于点(1,-2)上,位于点(3,-2)上,则位于点( )上.
A.(-1,1) B.(-1,2) C.(-2,1) D.(-2,2)
2.观察下列图象,与图①中的鱼相比,图②中的 ( http: / / www.21cnjy.com )鱼发生了一些变化,若图①中鱼上点P的坐标为(5,4),则这个点在图②中的对应点P1的坐标应为________.
( http: / / www.21cnjy.com )
① ②
3.(体验探究题)如图,A表示三经路与一纬路的十字路口,B表示一经路与三纬路的十字路口,如果用(3,1)→(3,2)→(3,3)→(2,3)→(1,3)表示由A到B的一条路线,用同样的方式写出另外一条由A到B的路径.
(3,1)→(_____)→(_____)→(_____)→(1,3)
测试点2 对称点、特殊点的坐标的特征
4.在平面直角坐标系中,点P(-1,4)关于原点的对称点是在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.在平面直角坐标系中,下列各点在第四象限的是( )
A.(2,1) B.(2,-1) C.(-2,1) D.(-2,-1)
6.已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′C′与△ABC关于y轴对称,则点A的对应点A′的坐标为( )
A.(-4,2) B.(-4,-2)
C.(4,-2) D.(4,2)
◆课后测控
1.在平面直角坐标系中,点P(-2,3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2006,河北)在平面直角坐标系中,若点P(x-2,x)在第二象限,则x的取值范围为( )
A.0
3.若点P(a,b)在第四象限,则点Q(-a,b-1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.点M(2,-3)关于y轴的对称点N的坐标是( )
A.(-2,-3) B.(-2,3) C.(2,3) D.(-3,2)
5.在直角坐标系中,如图所示,右边的图案是左边的图案经过平移得到,左图中左右眼睛的坐标分别是(-4,2),(-2,2),右边图形中左眼的坐标是(3,4),则右图案中右眼的坐标是_______.
6.在平面直角坐标系中,点P(-2,3)关于原点的对称点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
7.根据指令[S,A](S≥0.0° ( http: / / www.21cnjy.com )
(2)请你给机器人下一个指令_________,使其移动到点(-5,5).
8.已知a是整数,点A(2a+1,2+a)在第二象限,则a=_______.
9.如图所示在直角坐标系中,射线Ox绕原点O逆时针旋转330°到OA的位置,若OP=2,则点P的坐标为_______.
10.已知△ABC的顶点坐标分别为:A(-7,0),B(1,0),C(-3,4),求△ABC的面积.
◆拓展创新
如图,我们给中国 ( http: / / www.21cnjy.com )象棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
(1)写出下一步“马”可能到达的点的坐标_______;
(2)顺次连接(1)中的所有点,得到的图形是_______图形(填“中心对称”、“旋转对称”、“轴对称”);
(3)指出(1)中关于点P成中心对称的点_________.
3.3图形与坐标
一、选择题
1.下列各点,在第二象限内的是 ( )
A.(-1,0) B.(2,2) C.(-2,3) D.(-2,-3)
2.已知点P的坐标为 (-2,0),则下列说法正确的是 ( )
A.点P在x轴上 B.点P在y轴上 C.点P在第一象限 D.点P在第三象限
3.如果点P(m + 3,m + 1)在x轴上,则点P坐标为 ( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
4.与直角坐标平面内的点对应的坐标是( )
A.一对实数 B.一对有序实数 C.一对有理数 D.一对有序有理数
5.在平面直角坐标系中,点P(-1,1)关于x轴的对称点在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.若点P(x, y) 在第二象限,且到x轴的距离为3,到y轴的距离为2,则点P坐标为 ( )
A. (2, 3) B.(-2, 3) C.(2, -3) D.( 3, -2)
7. 电影票上“6排3号”,记作(6,3),则8排6号记作( )毛
A.(6,3) B.(6,8) C.(8,3) D.(8,6)
二、填空题
8.若点P (-3, a)在第二象限角平分线上,则a = .
9.已知矩形ABCD三个顶点的坐标A (-1, -1),B (-1, 1),
C (2, 1),点D的坐标是 .
10.点A在(-3,2) ( http: / / www.21cnjy.com )在平面直角坐标系中向右平移5个单位得到点B,则点B的坐标为________,点B关于x轴的对称点的坐标为________,点B关于y轴的对称点的坐标为___________.
11.点M(-2,3)到x轴的距离为_______,到y轴的距离为______.
三、解答题
12.如图,点A表示2街与4大道的十 ( http: / / www.21cnjy.com )字路口,点B表示4街与2大道的十字路口, 如果用(2,4)→(2,3)→(3,3)→(4,3)→(4,2)表示A到B的途径, 请你用同样的方法尽可能多地表示A到B的其它途径.
13.四边形OABC在平面直角坐标系中的位置如图所示:
⑴写出右图中四边形OABC各顶点的
坐标;
⑵线段BC与横坐标、纵坐标有什么特殊的位置关系?
⑶四边形OABC是什么特殊四边形?
14.在下图中找出下列各点,并将
各点用线段首尾顺次连结起来,观察所得的图形,你觉得它像什么?
(1,1),(3,4),(3,3),(7,3),(8,2),(8,0),(7,1),(4,1),(3,0),(3,1)
15.如下图所示,已知 ( http: / / www.21cnjy.com )OABC在平面直角坐标系中三顶点的坐标分别为O(0,0),A(4,2),B(0,3),另一顶点C未标出,试根据已知三点确定点C的坐标,并画出平行四边形.
16:已知△ABC 在直角坐标系中的位 ( http: / / www.21cnjy.com )置如图4所示,如果△A'B'C' 与△ABC 关于y轴对称,那么点A的对应点A'的坐标为( ). A.(-4,2) B.(-4,-2) C.(4,-2) D.(4,2)
【基础概念】
1、平面上物体的位置可以用有序实数对来确定。
2、在平面内确定物体的位置一般需要几个数据 有哪些方法
(1)用有序数对来确定;
(2)用方向和距离(方位)来确定;
3、在平面内有公共原点而且互相垂直的两条数轴,就构成了平面直角坐标系。简称直角坐标系,坐标系所在的平面就叫做坐标平面
4、掌握各象限上及x轴,y轴上点的坐标的 特点:
第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-)
5、x轴上的点纵坐标为0,表示为(x,0);y轴上的点横坐标为0,表示为(0,y)
6、(1)关于x轴对称的两点:横坐标相同,纵坐标互为相反数。
(2)关于y轴对称的两点:纵坐标相同,横坐标互为相反数。
(3)关于原点对称的两点:横坐标互为相反数,纵坐标互为相反数。
§3.3 轴对称和平移的坐标表示
学习目标:1、掌握点平移得到新坐标的规律,并且熟练画出图形。
2、理解“数形结合”;体会坐标系中图形平移的实际应用。
学习重点:探究点或图形平移引起的的坐标的变化规律。
学习难点:如何正确理解图形在坐标系中的平移变换。
☆ 自主学习 ☆
一、链接:
在平面直角坐标系中,描出下列各点,并将
各点用线段依次连接起来:
(1,1) (2,3) (3,1) (4,3) (5,1)
观察得到的图形,你觉得它像什么?
二、导读:预习课本,完成以下题目:
如图,按下列要求在直角坐标系中标出点。
(1)将点A(-1,-2)向右平移5个单位
长度得到A1点的坐标为 。
(2)将点A(-1,-2)向左平移2个单位
长度得到A2点的坐标为 。
(3)将点A(-1,-2)向上平移4个单位
长度得到A3点的坐标为 。
(4)将点A(-1,-2)向下平移1个单位
长度得到A4点的坐标为
总结:坐标系中,点的上下平移,只改变它的___坐标;点的左右平移,只改变它的___坐标;
三、预习反思:通过预习,你还有哪些疑惑呢 请将它写下来,你准备怎样解决
☆ 合作探究 ☆
1、思考一下坐标系中点的平移与坐标变化之间的关系,试填空:
(1)点的横坐标每增加1个单位,那么这个点将向___移动1个单位。
(2)点的横坐标每减少1个单位,那么这个点将向___移动1个单位。
(3)点的纵坐标每增加1个单位,那么这个点将向___移动1个单位。
(4)点的纵坐标每减少1个单位,那么这个点将向___移动1个单位。
(5)已知点P(-3,5),如果把它向上平移6个单位,再向左平移4个单位,得到点Q,则Q点的坐标是__________。
2、如图:铅笔图案的五个顶点的坐标分别
是(0,1)(4,1)(5,1.5)(4,2)
(0,2),将图案向下平移2个单位长度,
作出相应图案,并写出平移后相应5点
的坐标。
3、从上题你发现点向左(或右),向上(或下)移动的规律了吗?试填空:
(1)将点(x,y)向右平移a个单位长度,可得对应点( , )。
(2)将点(x,y)向左平移a个单位长度,可得对应点( , )。
(3)将点(x,y)向上平移a个单位长度,可得对应点( , )。
(4)将点(x,y)向下平移a个单位长度,可得对应点( , )。
☆ 归纳反思 ☆
把平面直角坐标系中的一个图形,按下面的要求平移,那么图形上任一点的坐标(x,y)是如何变化的
①向左或向右移动a(a>0)个单位。
②向上或向下移动b(b>0)个单位。
③向左或向右移动a个单位,再向上或向下移动b个单位。
☆ 达标检测 ☆
1、如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是( )
(A)(2,-2),(3,4),(1,7)。
(B)(-2,2),(4,3),(1,7)。
(C)(-2,2),(3,4),(1,7)。
(D)(2,-2),(3,4),(2,6)。
2、在坐标系中,点P先向左平移4个单位,再向上平移2个单位后的坐标为(-1,0),则P点的坐标是_________。
3、已知三角形的三个顶点都在以下表格的交点上,其中A(3,3)、B(3,5),请在表格中
确定点C的位置,使 ( http: / / www.21cnjy.com )=2,这样的点C有多少个?请分别表示出来。
中学八年级上数学第四章函数导学案(1)
4.1.1变量与函数
学习目标:1、通过探索具体问题中的数量关系和变化规律来了解常量、变量的意义;
2、学会用含一个变量的代数式表示另一个变量;
学习重点:了解常量与变量的意义; 学习疑点:较复杂问题中常量与变量的识别
学习过程:
揭示目标,学法指导
问题一:汽车以60千米/小时的速度匀速行驶,行驶里程为s千米,行驶时间为t小时.
1.请同学们根据题意填写下表:
t/时 1 2 3 4 5 t
s/千米
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含t的式子表示s: s=________,t的取值范围是 _________ .
这个问题反映了匀速行驶的汽车所行驶的路程____随行驶时间___的变化过程.
二、学生探究,教师巡导
(一)问题探究:
问题二:1.电影院播放的电影《爸爸去哪儿》票价20元/张,请同学们根据题意填写下表:
售出票数(张) 早场150 午场206 晚场310 x
收入y (元)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含x的式子表示y: y=______ ,x的取值范围是 .
这个问题反映了票房收入_________随售票张数_________的变化过程.
问题三:弹簧伸长量为0.16m/kg,完成下列问题
1.请同学们根据题意填写下表:
所挂重物(kg) 1 2 3 4 5 m
受力后的弹簧长度L(cm)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含m的式子表示L: L=____________ ,m的取值范围是 .
这个问题反映了_________随_________的变化过程.
问题四:1.请同学们根据题意填写下表:(用含 ( http: / / www.21cnjy.com )的式子表示)
圆面积s(cm2) 10 20 30 s
半径r(cm)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含s的式子表示r.r=_________,s的取值范围是 .
这个问题反映了___ _ 随_ __的变化过程.
问题五:请看书第110页问题2,完成下列问题
1.请同学们根据题意填写下表:
长x(m) 1 2 3 4 x
正方形面积s(m2)
2.在以上这个过程中,变化的量是_____________.不变化的量是__________.
3.试用含x的式子表示s. S=__________________,x的取值范围是 .
这个问题反映了矩形的___ _ 随_ __的变化过程.
小结:以上这些问题都反映了不同事物的变化 ( http: / / www.21cnjy.com )过程,其实现实生活中还有好多类似的问题,在这些变化过程中,有些量的值是按照某种规律变化的,有些量的数值是始终不变的。
(二)得出结论: 在一个变化过程中,我们称数值发生变化的量为________;
在一个变化过程中,我们称数值始终不变的量为________;
三、学生展示,老师精导
学生展示以上探究的问题,老师强调“变化过程”,“变量”,“常量”的意义。
四、边练边清,巩固提升
1.齿轮每分钟120转,如果 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。表示转数,表示转动时间,那么用 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。表示的关系是 ,其中 为变量, 为常量.
2.摄氏温度C与华氏温度F之间的对应关系为 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。℃,则其中的变量是 ,常量是 。
3.在⊿中,它的底边是 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。,底边上的高是,则三角形的面积 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。,当底边的长一定时,在关系式中的常量是 ,变量是 。
4.在圆的周长 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。中,常量与变量分别是( )
(A) 2是常量,c、、 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。是变量 (B)2是常量,c、 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。是变量
(C) c、2是常量,是变量 (D)2是常量,c、 HYPERLINK "http://www.21cnjy.com" 错误!不能通过编辑域代码创建对象。是变量
5.小军用50元钱去买单价是8元的笔记本,则他剩余的钱Q(元)与他买这种笔记本的本数x之间的关系是 ( )
A.Q=8x B.Q=8x-50 C.Q=50-8x D.Q=8x+50
6.甲、乙两地相距S千米,某人行完全程 ( http: / / www.21cnjy.com )所用的时间t(时)与他的速度v(千米/时)满足vt=S,在这个变化过程中,下列判断中错误的是 ( )
A.S是变量 B.t是变量 C.v是变量 D.S是常量
课后反思:
你有什么收获?
4.1.2函数的表示法
学习目标:
(1)理解函数的概念,能准确识别出函数关系中的自变量和函数
(2)会用变化的量描述事物;(3)会用运动的观点观察事物,分析事物X|k |b| 1 . c|o |m
学习重点:函数的概念 学习难点:认识函数,领会函数的意义
学习过程:
揭示目标,学法指导:
1、请你举出生活中含有两个变量的变化过程,说明其中的常量和变量。
二、学生探究,教师巡导
请看书112——117页内容,完成下列问题:
思考书中第112页的说一说,归纳出变量之间的关系。
完成书上第113页的动脑筋,体会图形中体现的变量和变量之间的关系。
归纳出函数的定义,明确函数定义中必须要满足的条件。
归纳:一般的,在一个变化过程中,如果有___ ( http: / / www.21cnjy.com )___变量x和y,并且对于x的_______,y都有_________与其对应,那么我们就说x是__________,y是x的________。如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值。
三、学生展示,老师精导
1函数的定义:
必须是一个变化过程;
两个变量;
其中一个变量每取一个值 ,另一个变量有且有唯一值对它对应。
2、学生展示
例1:一辆汽车的油箱中现有汽油 ( http: / / www.21cnjy.com )50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:千米)的增加而减少,平均耗油量为0.1L/千米。
(1)写出表示y与x的函数关系式.
(2)指出自变量x的取值范围.
(3) 汽车行驶200千米时,油箱中还有多少汽油?
教师精导:函数自变量的取值范围与问题的实际意义。
四、边练边清,巩固提升
P106页:1,2题
1、判断下列变量之间是不是函数关系:
(1)长方形的宽一定时,其长与面积;
(2)等腰三角形的底边长与面积;
(3)某人的年龄与身高;
2.写出下列函数的解析式.
(1)一个长方体盒子高3cm,底面是正方形,这个长方体的体积为y(cm3),底面边长为x(cm),写出表示y与x的函数关系的式子.
(2)汽车加油时,加油枪的流量为10L/min.
①如果加油前,油箱里还有5 L油,写出在加油过程中,油箱中的油量y(L)与加油时间x(min)之间的函数关系;
②如果加油时,油箱是空的,写出在加油过程中,油箱中的油量y(L)与加油时间x(min) 之间的函数关系.
3.(2007.云南)某地在调整电 ( http: / / www.21cnjy.com )价时,为了鼓励居民节约用电,采取了居民用电分段计价的办法:若每月每户用电量不超过80度,按0.48元/ 度收费;用电量在80~180度(含180度)之间,超过80度的部分按0.56元/度收费;用电量在180度以上,超过180度的部分按0.62元/度收费.同时规定在实行调价的当月收费中,用电量的1/3按原电价0.42元/度收费,用电量的2/3按调价后的分段计价办法收费.以后各月的用电量全部按分段计价的办法收费.
课后反思:
你的收获:
你的疑问:
函数及其图象(3)
学习目标:1.知道函数图象的意义;2.能画出简单函数的图象,会列表、描点、连线;
3.能从图象上由自变量的值求出对应的函数的近似值。
学习重点:1.函数图像的画法;2.观察分析函数图像 学习疑点:分析概括图像中的信息
学习过程:
一、揭示目标,学法指导
1.什么是函数图像
2.如何作函数图像?具体步骤有哪些?
3.如何判定一个图像是函数图像,你判断的依据是什么
4.有哪些方法表示函数关系?各自的优缺点是什么?
二、学生探究,教师巡导
1.如图1是某地区一天的气温随时间变化的图象,根据图象回答:在这一天中:
(1)气温(℃) (填“是”或“不是”)时间(时)的函数.(2) 时气温最高, 时气温最低,最高汽温是 ℃,最低气温是 ℃.(3)10时的气温是 ℃.(4) ___时气温是4℃.(5) 时间内,气温不断上升.(6) 时间内,气温持续不变.
2等腰△ABC的周长为10cm,底边BC的长为ycm,腰AB的长为xcm.
(1)写出y关于x的函数关系式 (2)求x的取值范围
(3)求y的取值范围 (4)画出函数的图象
三、学生展示,老师精导
正确理解函数图象与实际问题间的内在联系
函数的图象是由一系列的( )组成,图象上每一点的坐标(x,y)代表了该函数关系的一对对应值。
1、读懂横、纵坐标分别所代表的实际意义;2、读懂两个量在变化过程中的相互关系及其变化规律。
这三种表示函数的方法各有优缺点。
1.用解析法表示函数关系 优点:简单明了。 ( http: / / www.21cnjy.com )能从解析式清楚看到两个( )之间的全部相依关系,并且适合进行理论分析和推导计算。缺点:在求对应值时,有时要做较复杂的计算。
2.用列表表示函数关系
优点:对于表中( )的每一个值,可以不 ( http: / / www.21cnjy.com )通过计算,直接把函数值找到,查询时很方便。缺点:表中不能把所有的自变量与函数对应值全部列出,而且从表中看不出变量间的对应规律。
3.用图象法表示函数关系
优点:形象直观,可以形象地反映出( )的趋势和某些性质,把抽象的函数概念形象化。缺点:从自变量的值常常难以找到对应的函数的准确值。
函数的三种基本表示方法,各有各 ( http: / / www.21cnjy.com )的优点和缺点,因此,要根据不同问题与需要,灵活地采用不同的方法。在数学或其他科学研究与应用上,有时把这三种方法结合起来使用,即由已知的函数解析式,列出自变量与对应的函数值的表格,再画出它的图象。
四、边练边清,巩固提升
1.若点p在第二象限,且p点到x轴的距离为,到y轴的距离为1,则p点的坐标是( )
A.(-1, HYPERLINK "http://www.21cnjy.com" ) B.(- HYPERLINK "http://www.21cnjy.com" ,1) C.( HYPERLINK "http://www.21cnjy.com" ,-1) D.(1,- HYPERLINK "http://www.21cnjy.com" )
2.下列函数中,自变量取值范围选取错误的是( )
A. HYPERLINK "http://www.21cnjy.com" 中,x取全体实数 B. HYPERLINK "http://www.21cnjy.com" 中, HYPERLINK "http://www.21cnjy.com" C. HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" D. HYPERLINK "http://www.21cnjy.com" 中, HYPERLINK "http://www.21cnjy.com"
3.(常州市,2000)小明的父亲饭后出去散 ( http: / / www.21c
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
