人教版(2019)选择性必修一 1.3 动量守恒定律 课件(共26张PPT)
文档属性
| 名称 | 人教版(2019)选择性必修一 1.3 动量守恒定律 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-16 18:24:54 | ||
图片预览





文档简介
(共26张PPT)
第一章 动量守恒定律
1.3 动量守恒定理
生活现象
这些生活现象中相互作用的物体的动量都发生了变化,但它们遵循着怎样的变化规律呢?
运动的A滑块和等质量且静止的B滑块碰撞
A
B
回顾第1节:碰撞中不变量的探究
实验探究
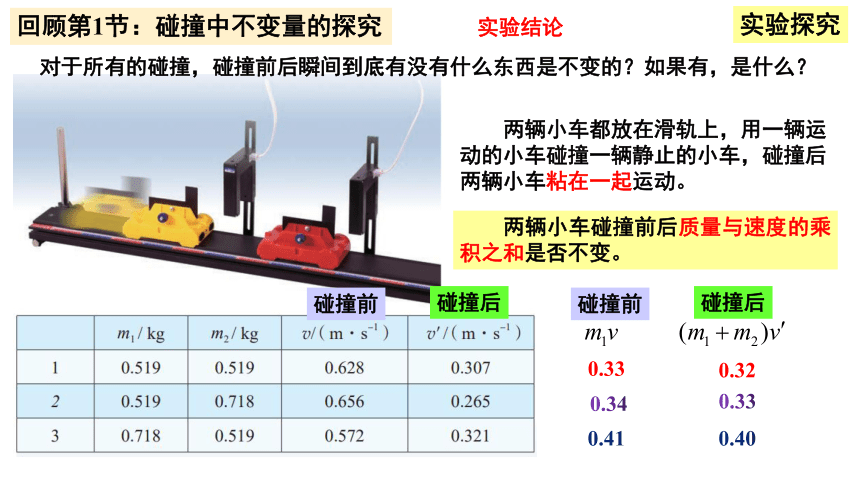
对于所有的碰撞,碰撞前后瞬间到底有没有什么东西是不变的?如果有,是什么?
两辆小车都放在滑轨上,用一辆运动的小车碰撞一辆静止的小车,碰撞后两辆小车粘在一起运动。
碰撞前
碰撞后
实验结论
碰撞前
碰撞后
0.33
0.32
0.34
0.33
0.41
0.40
两辆小车碰撞前后质量与速度的乘积之和是否不变。
回顾第1节:碰撞中不变量的探究
碰后A停下,B运动,且两滑块通过光电门时间相等,那么碰前A滑块的速度等于碰后B滑块的速度。
回顾第1节:碰撞中不变量的探究
即碰前A的动量与碰后B的动量相同,则碰前A、B总动量与碰后A、B总动量相同。
根据大量探究发现:在碰撞前后,两个物体的总动量是不变的。
是巧合,还是必然?有没有什么条件?能否从理论角度分析确定?
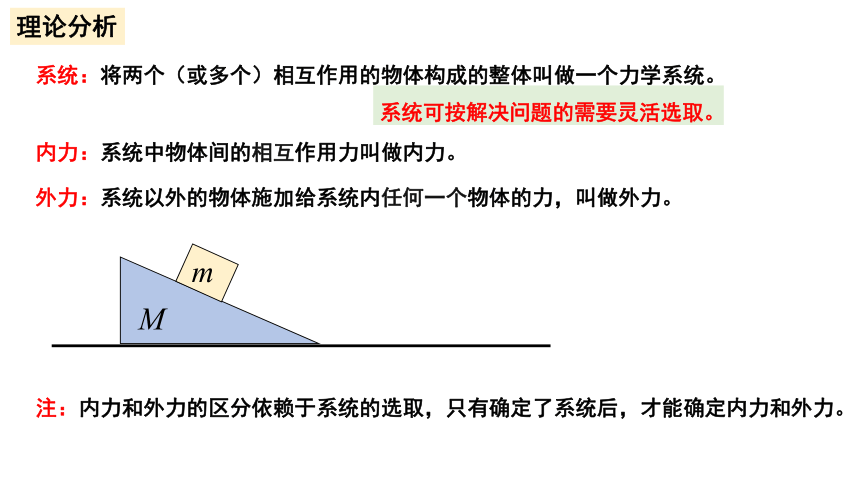
注:内力和外力的区分依赖于系统的选取,只有确定了系统后,才能确定内力和外力。
系统:将两个(或多个)相互作用的物体构成的整体叫做一个力学系统。
内力:系统中物体间的相互作用力叫做内力。
外力:系统以外的物体施加给系统内任何一个物体的力,叫做外力。
理论分析
系统可按解决问题的需要灵活选取。
在光滑水平面上做匀速运动的两个物体A、B,质量分别为m1和m2,沿着同一直线向相同的方向运动,速度分别是v1、v2,且v2>v1。当B追上了A时发生碰撞。碰撞后A、B的速度分别为v1′和v2′。
B
v2
m2
A
v1
m1
若要研究碰撞前后两物体的动量之和,该如何分析?
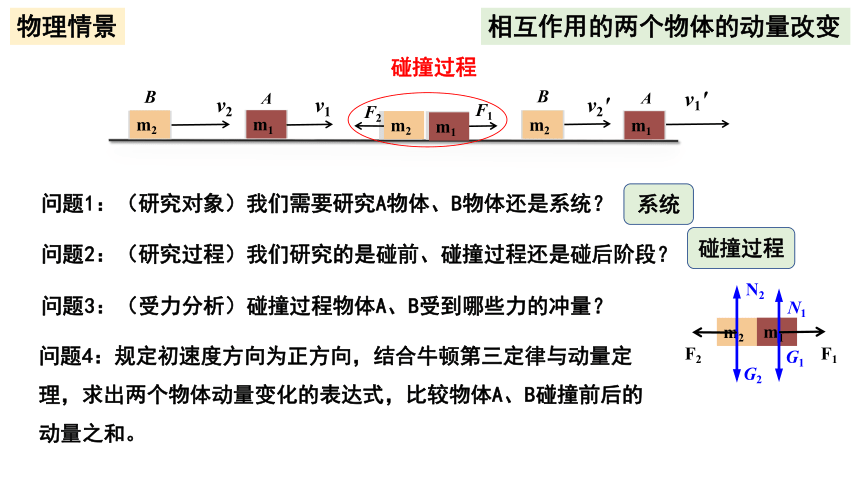
相互作用的两个物体的动量改变
物理情景
问题1:(研究对象)我们需要研究A物体、B物体还是系统?
B
v2
m2
A
v1
m1
B
v2'
m2
A
v1'
m1
碰撞过程
F1
F2
m2
m1
问题2:(研究过程)我们研究的是碰前、碰撞过程还是碰后阶段?
系统
碰撞过程
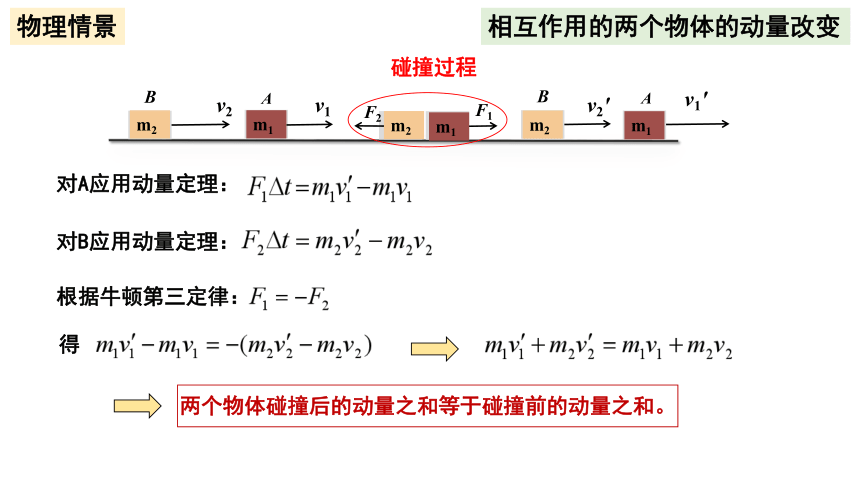
相互作用的两个物体的动量改变
物理情景
F2
F1
m2
m1
G1
N1
N2
G2
问题3:(受力分析)碰撞过程物体A、B受到哪些力的冲量?
问题4:规定初速度方向为正方向,结合牛顿第三定律与动量定理,求出两个物体动量变化的表达式,比较物体A、B碰撞前后的动量之和。
对A应用动量定理:
对B应用动量定理:
根据牛顿第三定律:
得
两个物体碰撞后的动量之和等于碰撞前的动量之和。
相互作用的两个物体的动量改变
物理情景
B
v2
m2
A
v1
m1
B
v2'
m2
A
v1'
m1
碰撞过程
F1
F2
m2
m1
m2
m1
这两个物体碰撞前后动量和不变,碰撞时受力情况是怎样?
F1
F2
N1
G1
N2
G2
两个碰撞物体外部作用力的矢量和为0的情况下动量守恒。
系统
(1)A、B看成系统,哪些力是外力?
矢量和为零
G2、N2、G1、N1
(2)A、B看成系统,外力矢量和是多少?
动量守恒定律
相互作用的两个物体的动量改变
物理情景
B
v2
m2
A
v1
m1
B
v2'
m2
A
v1'
m1
碰撞过程
F1
F2
m2
m1
如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
系统:相互作用的两个(或多个)物体
例如两个小球碰撞时,就可把它们看成一个系统。
外力:系统以外的物体对系统内的物体施加的力
内力:系统内物体之间彼此施加给对方的作用力
例如两个小球在光滑桌面上碰撞时,小球之间的撞击力属于内力;桌面给小球的支持力,以及小球的重力,属于外力。
总动量保持不变:系统内各物体动量的矢量和不变,但每个物体的动量可以发生变化。
得出结论
物理情景
1、研究对象:相互作用的一个系统
若是两个物体构成的系统,则是:
动量守恒定律
2、守恒的条件:不受外力或所受外力之和为0
3、表达式:
或者
绝对守恒:系统合外力为零
内力不改变系统总动量,
内力改变的是系统内每个物体的动量。
适用于正碰,斜碰:
动量守恒定律不仅适用于碰撞,也适用于任何形式的相互作用,不仅适用于两个物体组成的系统,还适用于多个物体的系统。微观、宏观、高速、低速均可。但需要符合守恒条件。
动量守恒定律的适用范围
例1:质量为m的子弹以水平速度v0射向静止在光滑水平面上的质量为M的木块,并留在木块中不再射出,求木块和子弹的共同速度。
v0
v共
牛顿运动定律要涉及整个过程中的力和状态,而动量守恒定律只涉及初末两个状态;
牛顿运动定律只适合于宏观、低速问题,但动量守恒定律还适用于微观、高速问题。
动量守恒定律的简单应用
例2:在下列几种现象中,动量守恒的是( )
A、在静止的光滑水平面上,车上的人从车头走向车尾
B、水平放置的轻弹簧,一辆固定于墙上,另一端与置于光滑水平面上的物体相连,开始时弹簧已有伸长,放手后物体在弹力的作用下运动
C、甲、乙两队进行拔河比赛,甲队获胜
D、汽车拉着拖车在平直的公路上做匀速直线运动,某时刻拖车突然脱钩离开汽车,由于司机没有发觉而保持汽车的驱动力不变,在拖车没有完全停下来的任何一段时间
A D
动量守恒定律的简单应用
两小车在运动过程中,相互排斥的磁力属于内力,整个系统的外力即重力和支持力的和为零,所以系统动量守恒。
动量守恒定律的简单应用
例3:在光滑水平面上有两个载有磁铁的相向运动的小车,两小车组成的系统动量守恒吗
系统所受的外力有:重力、地面对木块支持力、竖直墙对弹簧的支持力,三者之和不为零,所以系统动量不守恒。
从守恒定义看:
从守恒条件看:
初状态
末状态
墙壁对弹簧有弹力
研究:
哪几个物体组成的系统?
什么过程?
机械能守恒情况呢?
动量守恒定律的简单应用
已知水平面光滑,子弹水平射入木块后留在木块中,丙者以相同的速度压缩弹簧。
例4:(对动量守恒条件的理解)小车与木箱紧挨着静放在光滑的水平冰面上,现有一男孩站在小车上用力向右迅速推出木箱,关于上述过程,下列说法正确的是( C )
A.男孩和木箱组成的系统动量守恒
B.小车与木箱组成的系统动量守恒
C.男孩、小车与木箱三者组成的系统动量守恒
D.木箱的动量增量与男孩、小车的总动量增量相同
动量守恒定律的简单应用
例5:质量m1=10 g的小球在光滑的水平桌面上以30 cm/s的速率向右运动,恰遇上质量为m2=50 g的小球以10 cm/s的速率向左运动,碰撞后,小球m2恰好停止,则碰后小球m1的速度大小和方向如何?
m2
v2
v1
m1
解:碰撞过程中,两小球组成的系统所受合外力为零,动量守恒.设向右为正方向。
由动量守恒定律列: m1v1+m2v2=m1v1′+m2v2′
代入数据解得: v1′=-20 cm/s
方向向左
动量守恒定律的简单应用
例6:在列车编组站里,一辆质量为1.8×104 kg 的货车在平直轨道上以2m/s的速度运动,碰上一辆质量为2.2×104 kg的静止货车,它们碰撞后结合在一起继续运动。求碰撞后运动的速度。
动量守恒定律的简单应用
碰撞过程时间非常短
(一般指硬碰硬)
碰撞过程的特点
内力远大于外力,系统动量守恒
研究对象?
研究过程?
动量守恒定律的简单应用
m1
m2
v1
v2=0
v
+
解:
取两货车系统为研究对象,在两车碰撞过程中,由于内力远大于外力,系统动量守恒。
取货车运动方向为正方向。
由动量守恒:
得共同速度:
2、近似守恒:系统的内力远大于外力
例7:一个质量为m,速度为v的子弹数值向上射穿质量为M的木块后继续上升,子弹从射穿木块再回到原木块处的时间为T,那么当子弹射出木块后,木块上升的最大高度是多少?
动量守恒定律的简单应用
v
v1
v2
子弹射穿木块的过程中,子弹与木块组成的系统动量近似守恒。
木块上升的最大高度:
Mg
F
mg
F`
F>>mg,且作用时间极短,mg的冲量可忽略。
在碰撞、打击、爆炸等相互作用时间极短的过程中,由于系统内部相互作用力远大于外力,往往可忽略外力的冲量,系统动量守恒近似成立。
一质量为m,速度为v的子弹数值向上射穿质量为M的木块后继续上升,子弹从射穿木块再回到原木块处的时间为T,木块上升的最大高度是多少?
动量守恒定律的简单应用
研究对象?
m
m1
v1
v2
m-m1
体会:
爆炸、碰撞的特点;
用动量守恒解这类问题的优势
爆炸过程中系统动量守恒吗?
动量守恒方程?
得
+
以炸裂前速度方向为正方向
如何判断另一块的速度方向?
3、某方向合外力为零,则在这个方向动量守恒
动量守恒定律的简单应用
例8:一辆质量为M的小车以速率v1在光滑的水平面上运动时,恰遇一质量为m,速率为v2物体以俯角60。的速度方向落在车上并陷于车里的砂中,求此后车的速度。
60。
v2
v1
v’
系统水平方向不受外力,水平方向动量守恒:(取v2方向为正向)
动量守恒定律的简单应用
一个系统不受外力或者所受外力之和为零,这个系统的总动量保持不变。
研究对象:
系统
成立条件:
1. 绝对守恒:不受外力或外力之和为零
内力不改变系统总动量,
内力改变的是系统内每个物体的动量
2. 方向守恒:某一方向上动量守恒:
系统在某一方向上不受外力或所受外力之和为零。
3. 近似守恒:
系统的内力远大于外力,且作用时间极短。
例如:打击、爆炸、碰撞
动量守恒定律
总结与回顾
第一章 动量守恒定律
1.3 动量守恒定理
生活现象
这些生活现象中相互作用的物体的动量都发生了变化,但它们遵循着怎样的变化规律呢?
运动的A滑块和等质量且静止的B滑块碰撞
A
B
回顾第1节:碰撞中不变量的探究
实验探究
对于所有的碰撞,碰撞前后瞬间到底有没有什么东西是不变的?如果有,是什么?
两辆小车都放在滑轨上,用一辆运动的小车碰撞一辆静止的小车,碰撞后两辆小车粘在一起运动。
碰撞前
碰撞后
实验结论
碰撞前
碰撞后
0.33
0.32
0.34
0.33
0.41
0.40
两辆小车碰撞前后质量与速度的乘积之和是否不变。
回顾第1节:碰撞中不变量的探究
碰后A停下,B运动,且两滑块通过光电门时间相等,那么碰前A滑块的速度等于碰后B滑块的速度。
回顾第1节:碰撞中不变量的探究
即碰前A的动量与碰后B的动量相同,则碰前A、B总动量与碰后A、B总动量相同。
根据大量探究发现:在碰撞前后,两个物体的总动量是不变的。
是巧合,还是必然?有没有什么条件?能否从理论角度分析确定?
注:内力和外力的区分依赖于系统的选取,只有确定了系统后,才能确定内力和外力。
系统:将两个(或多个)相互作用的物体构成的整体叫做一个力学系统。
内力:系统中物体间的相互作用力叫做内力。
外力:系统以外的物体施加给系统内任何一个物体的力,叫做外力。
理论分析
系统可按解决问题的需要灵活选取。
在光滑水平面上做匀速运动的两个物体A、B,质量分别为m1和m2,沿着同一直线向相同的方向运动,速度分别是v1、v2,且v2>v1。当B追上了A时发生碰撞。碰撞后A、B的速度分别为v1′和v2′。
B
v2
m2
A
v1
m1
若要研究碰撞前后两物体的动量之和,该如何分析?
相互作用的两个物体的动量改变
物理情景
问题1:(研究对象)我们需要研究A物体、B物体还是系统?
B
v2
m2
A
v1
m1
B
v2'
m2
A
v1'
m1
碰撞过程
F1
F2
m2
m1
问题2:(研究过程)我们研究的是碰前、碰撞过程还是碰后阶段?
系统
碰撞过程
相互作用的两个物体的动量改变
物理情景
F2
F1
m2
m1
G1
N1
N2
G2
问题3:(受力分析)碰撞过程物体A、B受到哪些力的冲量?
问题4:规定初速度方向为正方向,结合牛顿第三定律与动量定理,求出两个物体动量变化的表达式,比较物体A、B碰撞前后的动量之和。
对A应用动量定理:
对B应用动量定理:
根据牛顿第三定律:
得
两个物体碰撞后的动量之和等于碰撞前的动量之和。
相互作用的两个物体的动量改变
物理情景
B
v2
m2
A
v1
m1
B
v2'
m2
A
v1'
m1
碰撞过程
F1
F2
m2
m1
m2
m1
这两个物体碰撞前后动量和不变,碰撞时受力情况是怎样?
F1
F2
N1
G1
N2
G2
两个碰撞物体外部作用力的矢量和为0的情况下动量守恒。
系统
(1)A、B看成系统,哪些力是外力?
矢量和为零
G2、N2、G1、N1
(2)A、B看成系统,外力矢量和是多少?
动量守恒定律
相互作用的两个物体的动量改变
物理情景
B
v2
m2
A
v1
m1
B
v2'
m2
A
v1'
m1
碰撞过程
F1
F2
m2
m1
如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
系统:相互作用的两个(或多个)物体
例如两个小球碰撞时,就可把它们看成一个系统。
外力:系统以外的物体对系统内的物体施加的力
内力:系统内物体之间彼此施加给对方的作用力
例如两个小球在光滑桌面上碰撞时,小球之间的撞击力属于内力;桌面给小球的支持力,以及小球的重力,属于外力。
总动量保持不变:系统内各物体动量的矢量和不变,但每个物体的动量可以发生变化。
得出结论
物理情景
1、研究对象:相互作用的一个系统
若是两个物体构成的系统,则是:
动量守恒定律
2、守恒的条件:不受外力或所受外力之和为0
3、表达式:
或者
绝对守恒:系统合外力为零
内力不改变系统总动量,
内力改变的是系统内每个物体的动量。
适用于正碰,斜碰:
动量守恒定律不仅适用于碰撞,也适用于任何形式的相互作用,不仅适用于两个物体组成的系统,还适用于多个物体的系统。微观、宏观、高速、低速均可。但需要符合守恒条件。
动量守恒定律的适用范围
例1:质量为m的子弹以水平速度v0射向静止在光滑水平面上的质量为M的木块,并留在木块中不再射出,求木块和子弹的共同速度。
v0
v共
牛顿运动定律要涉及整个过程中的力和状态,而动量守恒定律只涉及初末两个状态;
牛顿运动定律只适合于宏观、低速问题,但动量守恒定律还适用于微观、高速问题。
动量守恒定律的简单应用
例2:在下列几种现象中,动量守恒的是( )
A、在静止的光滑水平面上,车上的人从车头走向车尾
B、水平放置的轻弹簧,一辆固定于墙上,另一端与置于光滑水平面上的物体相连,开始时弹簧已有伸长,放手后物体在弹力的作用下运动
C、甲、乙两队进行拔河比赛,甲队获胜
D、汽车拉着拖车在平直的公路上做匀速直线运动,某时刻拖车突然脱钩离开汽车,由于司机没有发觉而保持汽车的驱动力不变,在拖车没有完全停下来的任何一段时间
A D
动量守恒定律的简单应用
两小车在运动过程中,相互排斥的磁力属于内力,整个系统的外力即重力和支持力的和为零,所以系统动量守恒。
动量守恒定律的简单应用
例3:在光滑水平面上有两个载有磁铁的相向运动的小车,两小车组成的系统动量守恒吗
系统所受的外力有:重力、地面对木块支持力、竖直墙对弹簧的支持力,三者之和不为零,所以系统动量不守恒。
从守恒定义看:
从守恒条件看:
初状态
末状态
墙壁对弹簧有弹力
研究:
哪几个物体组成的系统?
什么过程?
机械能守恒情况呢?
动量守恒定律的简单应用
已知水平面光滑,子弹水平射入木块后留在木块中,丙者以相同的速度压缩弹簧。
例4:(对动量守恒条件的理解)小车与木箱紧挨着静放在光滑的水平冰面上,现有一男孩站在小车上用力向右迅速推出木箱,关于上述过程,下列说法正确的是( C )
A.男孩和木箱组成的系统动量守恒
B.小车与木箱组成的系统动量守恒
C.男孩、小车与木箱三者组成的系统动量守恒
D.木箱的动量增量与男孩、小车的总动量增量相同
动量守恒定律的简单应用
例5:质量m1=10 g的小球在光滑的水平桌面上以30 cm/s的速率向右运动,恰遇上质量为m2=50 g的小球以10 cm/s的速率向左运动,碰撞后,小球m2恰好停止,则碰后小球m1的速度大小和方向如何?
m2
v2
v1
m1
解:碰撞过程中,两小球组成的系统所受合外力为零,动量守恒.设向右为正方向。
由动量守恒定律列: m1v1+m2v2=m1v1′+m2v2′
代入数据解得: v1′=-20 cm/s
方向向左
动量守恒定律的简单应用
例6:在列车编组站里,一辆质量为1.8×104 kg 的货车在平直轨道上以2m/s的速度运动,碰上一辆质量为2.2×104 kg的静止货车,它们碰撞后结合在一起继续运动。求碰撞后运动的速度。
动量守恒定律的简单应用
碰撞过程时间非常短
(一般指硬碰硬)
碰撞过程的特点
内力远大于外力,系统动量守恒
研究对象?
研究过程?
动量守恒定律的简单应用
m1
m2
v1
v2=0
v
+
解:
取两货车系统为研究对象,在两车碰撞过程中,由于内力远大于外力,系统动量守恒。
取货车运动方向为正方向。
由动量守恒:
得共同速度:
2、近似守恒:系统的内力远大于外力
例7:一个质量为m,速度为v的子弹数值向上射穿质量为M的木块后继续上升,子弹从射穿木块再回到原木块处的时间为T,那么当子弹射出木块后,木块上升的最大高度是多少?
动量守恒定律的简单应用
v
v1
v2
子弹射穿木块的过程中,子弹与木块组成的系统动量近似守恒。
木块上升的最大高度:
Mg
F
mg
F`
F>>mg,且作用时间极短,mg的冲量可忽略。
在碰撞、打击、爆炸等相互作用时间极短的过程中,由于系统内部相互作用力远大于外力,往往可忽略外力的冲量,系统动量守恒近似成立。
一质量为m,速度为v的子弹数值向上射穿质量为M的木块后继续上升,子弹从射穿木块再回到原木块处的时间为T,木块上升的最大高度是多少?
动量守恒定律的简单应用
研究对象?
m
m1
v1
v2
m-m1
体会:
爆炸、碰撞的特点;
用动量守恒解这类问题的优势
爆炸过程中系统动量守恒吗?
动量守恒方程?
得
+
以炸裂前速度方向为正方向
如何判断另一块的速度方向?
3、某方向合外力为零,则在这个方向动量守恒
动量守恒定律的简单应用
例8:一辆质量为M的小车以速率v1在光滑的水平面上运动时,恰遇一质量为m,速率为v2物体以俯角60。的速度方向落在车上并陷于车里的砂中,求此后车的速度。
60。
v2
v1
v’
系统水平方向不受外力,水平方向动量守恒:(取v2方向为正向)
动量守恒定律的简单应用
一个系统不受外力或者所受外力之和为零,这个系统的总动量保持不变。
研究对象:
系统
成立条件:
1. 绝对守恒:不受外力或外力之和为零
内力不改变系统总动量,
内力改变的是系统内每个物体的动量
2. 方向守恒:某一方向上动量守恒:
系统在某一方向上不受外力或所受外力之和为零。
3. 近似守恒:
系统的内力远大于外力,且作用时间极短。
例如:打击、爆炸、碰撞
动量守恒定律
总结与回顾
